Как посчитать хорду окружности
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать хорду окружности
Чтобы посчитать хорду круга (окружности) просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
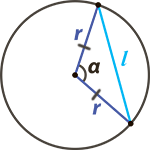
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
угол α °
Ответ:
0
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
угол α рад
Ответ:
0
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
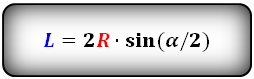
l = 2r⋅sinα/2
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
См. также
Формула длины хорды окружности
Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.
L — хорда
R — радиус окружности
O — центр окружности
α — центральный угол
Формула длины хорды, (L):
Калькулятор для расчета длины хорды окружности :
Дополнительные формулы для окружности:
- Подробности
-
Автор: Administrator
-
Опубликовано: 16 октября 2011
-
Обновлено: 13 августа 2021

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота
Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Площадь сегмента:
[1]
Длина дуги:
Длина хорды:
Высота сегмента:
Сегмент
Угол в градусах, образуемый радиусами сектора
Точность вычисления
Знаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Параметры сегмента по хорде и высоте
Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Площадь сегмента круга по радиусу и высоте
Точность вычисления
Знаков после запятой: 2
Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Круговой сегмент — все варианты расчета
Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Секущая и хорда окружности
Зачем что-то знать о секущих и хордах в окружности?
Как обычно, знание свойств и закономерностей сильно облегчает жизнь.
Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ!
Поехали!
Секущая и хорда окружности — коротко о главном
Секущая окружности
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Хорда окружности
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Длина хорды
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle AСB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB). Тогда:
( displaystyle AB=2Rsin alpha).
Произведение длин отрезков хорд и секущих
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется:
( displaystyle ABcdot AC=ADcdot AE).
Теорема о секущей и касательной
Для любых секущей и касательной, проходящих через точку ( A), верно:
( displaystyle A{{C}^{2}}=ADcdot AE).
А теперь подробнее…
Определения секущей и хорды окружности
Давай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки.
Здесь ( displaystyle AC) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках.
Здесь ( displaystyle BC) – хорда окружности – отрезок, соединяющий две точки на окружности.
Кстати, заметил ли ты, что на первом рисунке хорда ( displaystyle BC) является кусочком секущей ( displaystyle AC)?
Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас ( displaystyle AB) – она же снаружи, верно?
Что же мы должны знать о секущей и хорде окружности?
Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности.
Длина хорды окружности
Пусть ( displaystyle AB) – хорда, ( displaystyle R) – радиус, ( displaystyle angle ACB) – любой вписанный угол, опирающийся на хорду ( displaystyle AB).
Тогда ( Largefrac{AB}{sin alpha }=2R)
Узнал теорему синусов?
Значит, длину хорды окружности можно найти по формуле:
Произведение длин отрезков хорд и секущих
Сейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности.
Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами.
Произведение длин отрезков хорд окружности
Для любых двух хорд окружности, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Произведение длин отрезков секущих окружности
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( displaystyle ABcdot AC=ADcdot AE)
Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком?
Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом.
Вопрос второй: Как не перепутать, что на что умножать?
Произведение длин отрезков хорд окружности — доказательство
Повторим формулировку.
Для любых двух хорд, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
А теперь докажем.
Рассмотрим ( triangle ABD) и ( triangle AEC). У них углы ( displaystyle A) равны как вертикальные и ( angle DBC=angle DEC), потому что они опираются на одну дугу ( displaystyle DC).
Значит, ( displaystyle triangle ABDsim triangle AEC) по двум углам (вспоминаем признаки подобия треугольников).
Запишем, что же нам даёт это подобие (и откроем маленький секрет!).
Произведение длин отрезков секущих окружности — доказательство
Еще раз формулировку…
Для любых двух секущих, проходящих через некоторую точку ( displaystyle A), выполняется: ( ABcdot AC=ADcdot AE)
Снова рассмотрим ( displaystyle triangle ABD) и ( displaystyle triangle AEC).
- У них есть общий ( angle A);
- Четырехугольник ( BCED) — вписанный (срочно повторяем или читаем тему «Окружность. Вписанный угол»).
Значит, ( angle 1+angle 2=180{}^circ ) (сумма противоположных углов вписанного четырехугольника равна ( 180{}^circ )). Но ( angle 2+angle 3=180{}^circ ) — как смежные углы (смотри на картинку).
Что же получилось?
( left{ begin{array}{l}angle 1+angle 2=180{}^circ \angle 2+angle 3=180{}^circ end{array} right.Rightarrow angle 1=angle 3)
То есть ( underbrace{angle ACE}_{в triangle AEC}=underbrace{angle ADB}_{в triangle ABD }).
Из всего этого следует, что ( triangle AECsim triangle ABD) по двум углам (( angle A) – общий и ( angle ACE=angle ADB)).
Снова запишем отношение соответствующих сторон:
Теорема о секущей и касательной (секретное оружие)
А сейчас «секретное» оружие — теорема о секущей и касательной. Почему секретное?
Потому что множество задач ОГЭ и ЕГЭ можно решить с помощью этой теоремы. А акцент на ней в учебнике не делается. То есть ее как бы нет…
В предыдущем пункте мы выяснили, что ( ABcdot AC=ADcdot AE)
Но возникает вопрос: а что будет, если секущая ( AC) и «превратится» в касательную?
Видишь: осталось всего три зелёных точки? Оказывается, ничего страшного, всё почти так же. Формулируем:
Для любых секущей и касательной, проходящих через точку ( A), верно: ( Large A{{C}^{2}}=ADcdot AE).
Тут точки ( B) и ( C) как бы слились в одну – и на рисунке, и в формуле. Заметил?
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Хорда — под этим понятием понимается отрезок, который соединяет 2 любые точки, отмеченные на окружности.
Если хорда проходит через её центр, то она будет диаметром.
Для того, чтобы найти длину хорды l, можно воспользоваться следующей формулой:
l = 2R * sin(α/2).
Здесь: R — радиус окружности и α — центральный угол.
Кстати, диаметр как частный случай хорды, имеет самую максимальную длину.
Вообще, задача нахождения длины хорды нередко возникает перед инженерами, механиками или архитекторами.
Пример
Радиус окружности R равен 5 см.
Угол α равен 60 градусов.
Длина хорды будет равна: l = 2*5*sin(30°) = 2*5*0,5 = 5 см.