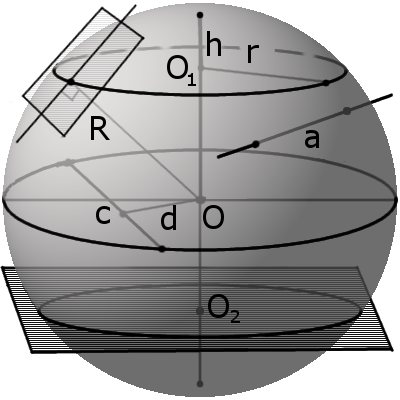
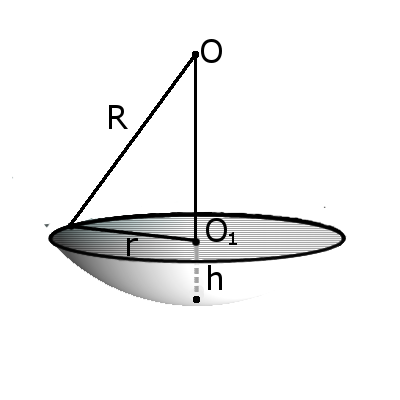
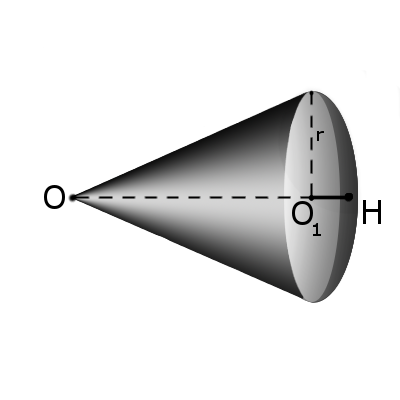
Как найти длину касательной к сфере - Исправление недочетов и поиск решений вместе с Examum.ru

§ 19. Шар и сфера

19.1. Определения шара, сферы и их элементов

С шаром и сферой мы уже знакомы. Напомним их определения.

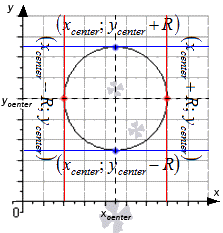
Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R (R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара.

Определение. Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.

Рис. 193

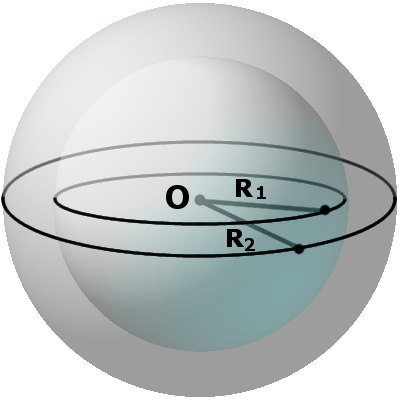
На рисунке 193 изображён шар с центром О и радиусом R = OА.

Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM < R (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R).

Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара (сферы). На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ, NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.

Рис. 194

Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F1 (рис. 194, б). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.

Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара (сферы). Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью; большая окружность является пересечением сферы и её диаметральной плоскости.

19.2. Изображение сферы

Рис. 195

Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором, а точки N и S — полюсами сферы. Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией.

Типичная ошибка (!) при изображении сферы (рис. 195, б) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V), а другую — профильной (обозначают W) плоскостями проекций.

Сферу расположим так, чтобы её ось N′S′ была параллельна профильной (W), но не параллельна фронтальной (V) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W; отрезки A1B1 и N1S1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C′D′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a; 196, a.

Рис. 196

Рис. 197

Обратите внимание! Полюсы N и S не лежат на абрисе, и экватор изображается эллипсом. При этом положение полюсов N и S и положение вершин А и В эллипса-экватора взаимосвязаны.

Действительно, из равенства △ОBF=△ЕNО (см.рис.196,а) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.

На рисунке 197, а — верное и наглядное изображение сферы, на рисунке 197, б — изображение сферы верное (почему?), но не наглядное; на рисунке 197, в — неверное изображение (почему?).

 ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.

Решение. Если ∠ АМВ = 90°, то точка М принадлежит окружности с диаметром АВ (рис. 198, a).

Рис. 198

Проведём произвольную плоскость α, содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB, есть сфера с диаметром AB. Точки А и В этому множеству точек-вершин не принадлежат.

19.3. Уравнение сферы

Составим уравнение сферы с центром А (a; b; с) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть М(x; у; z) — любая точка этой сферы (рис. 199). Тогда MA = R или MA2 = R2. Учитывая, что MA2 = (x – a)2 + (у – b)2 + (z – c)2, получаем искомое уравнение cферы

(x – a)2 + (у – b)2 + (z – c)2 = R2.

Если начало системы координат совпадает с центром A сферы, то a = b = c = 0, а сфера в такой системе координат имеет уравнение

x2 + y2 + z2 = R2.

Из полученных уравнений следует, что сфера — поверхность второго порядка.

Так как для любой точки М(х; у; z) шара с центром А (a; b; с) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством

(x – a)2 + (у – b)2 + (z – c)2 ⩽ R2.

При этом для всех внутренних точек М шара выполняется условие МА2 < R2, т. е.

Рис. 199

(х – a)2 + (у – b)2 + (z – c)2 < R2,

для точек М шаровой поверхности — условие

МА = R,

т. е. (х – a)2 + (у – b)2 + (z – c)2 = R2,

для точек М вне шара — условие

МА > R,

т. е. (х – a)2 + (у – b)2 + (z – c)2 > R2.

19.4. Пересечение шара и сферы с плоскостью

Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.

Теорема 30 (о пересечении шара и сферы с плоскостью). 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = , где R — радиус шара, a d — расстояние от центра шара до плоскости сечения. 2) Если расстояние от центра шара до данной плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку. 3) Если расстояние от центра шара до данной плоскости больше радиуса, то плоскость не имеет с шаром общих точек.

Доказательство. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α. Обозначим ρ(О; α) = | ОА | = d — расстояние от центра шара до плоскости α.

Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α.

Рис. 200

1) ρ(O; α) = d < R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = . Для этого достаточно убедиться, что любая точка пересечения шара и плоскости α есть точка круга с центром А и радиусом r = и, обратно, любая точка этого круга есть точка указанного пересечения.

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM2 = ОА2 + АМ2, откуда AM = . Так как точка М принадлежит шару, то ОМ ⩽ R, тогда OM2 – OA2 ⩽ R2 – d2, поэтому АМ ⩽ . Это означает, что точка М сечения шара плоскостью α находится от точки А на расстоянии, не большем , следовательно, она принадлежит кругу с центром А и радиусом .

Обратно, пусть М — произвольная точка плоскости α, принадлежащая кругу с центром А и радиусом r = . В прямоугольном треугольнике AOM по теореме Пифагора OM2 = ОA2 + AM2. Так как AM ⩽ r, то OM2 ⩽ OA2 + r2 = d2 + R2 – d2 = R2, откуда OM ⩽ R. Значит, точка М принадлежит данному шару. Учитывая, что точка М принадлежит и плоскости α, приходим к выводу: точка M принадлежит пересечению данного шара и плоскости α.

Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d < R пересечением сферы и плоскости является окружность с центром А и радиусом r = . Проделайте это самостоятельно.

Рис. 201

Если плоскость α проходит через центр O шара, то d = 0, значит, r = R, т. е. сечением шара такой плоскостью является большой круг, а сечением сферы — большая окружность (см. рис. 200).

2) ρ(O; α) = d = OA = R (рис. 201).

Так как ОА = ρ(O; α) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α, принадлежит шаровой поверхности, ограничивающей данный шар.

Рис. 202

Пусть M — произвольная точка плоскости α, отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α, удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.

3) ρ(О; α) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼

 ЗАДАЧА (3.161). Через середину радиуса шара проведена перпендикулярная к нему плоскость. Радиус шара равен R. Найти: а) площадь получившегося сечения; б) площади боковой и полной поверхностей конуса, основанием которого служит получившееся сечение шара, а вершиной — центр шара; в) площади боковой и полной поверхностей правильной треугольной пирамиды, вписанной в этот конус.

Решение. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD; α — секущая плоскость, проходящая через точку С перпендикулярно OD.

Рассмотрим сечение шара диаметральной плоскостью, проходящей через его радиус OD. Этим сечением является большой круг с центром О и радиусом R (рис. 203); АВ — диаметр круга — сечения данного шара плоскостью α.

Так как АВ ⟂ OD и точка С — середина радиуса OD, то отрезок AB равен стороне правильного треугольника, вписанного в окружность радиуса R, значит, АВ = R, откуда

Рис. 203

АС = r = , где r — радиус сечения шара плоскостью α. Тогда площадь этого сечения равна πr2 = .

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = .

Рис. 204

Образующая ОЕ конуса (рис. 204) равна радиусу R данного шара. Поэтому площадь боковой поверхности этого конуса равна

πr•R = π••R = ,

а площадь его полной поверхности — + = πR2•(2 + ).

в) Найдём площадь поверхности правильной треугольной пирамиды OEFK, вписанной в конус, радиус основания которого СK = r = , боковое ребро OE пирамиды равно радиусу R данного шара (см. рис. 204).

Так как △ ЕFK — правильный, вписанный в окружность радиуса r = , то сторона этого треугольника равна r , т. е. EF = . Тогда S△ EFK = = .

Площадь боковой поверхности пирамиды равна 3S△ EOF = EF•ОН, где OH — апофема пирамиды. В прямоугольном треугольнике OHF находим

ОН = = = .

Тогда EF•OH = — площадь боковой поверхности пирамиды.

Следовательно, площадь полной поверхности пирамиды равна

+ = R2( + ).

Ответ: a) ; б) π R2 (2 +); в) ; R2( +).

19.5. Плоскость, касательная к сфере и шару

Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.

Определение. Плоскость, имеющая только одну общую точку со сферой (с шаром), называется касательной плоскостью к сфере (шару), а их единственная общая точка называется точкой касания (рис. 205).

Рис. 205

Также говорят, что плоскость касается сферы (шара).

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Заметим, что если прямая a касается сферы в точке М, то эта прямая касается в точке М той окружности большого круга, которая является сечением сферы и диаметральной плоскости, проходящей через прямую a.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М, то эта прямая касается в точке М самой сферы.

Более того, так как прямая a, касающаяся сферы в точке М, имеет со сферой лишь одну общую точку — точку М, то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R, точка А — центр окружности радиуса r, по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R•cos ϕ (△ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).

Для плоскости, касательной к сфере, справедливы теоремы, аналогичные теоремам о прямой, касательной к окружности на плоскости.

Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.

Доказательство. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α, касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α.

Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α. Значит, расстояние от центра сферы до плоскости α, равное длине перпендикуляра, проведённого из центра О на плоскость α, меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α. Теорема доказана. ▼

Справедлива обратная теорема.

Теорема 32. Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведённому в эту точку, то она касается сферы.

Доказательство. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M). Теорема доказана.▼

Так как сечение шара плоскостью есть круг, то можно доказать, что для шара выполняются следующие метрические соотношения:

—диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;

—отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);

—произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R2 – a2, где R — радиус шара, a — расстояние от центра шара до данной точки);

—если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a2 – R2, где R — радиус шара, a — расстояние от центра шара до данной точки).

19.6. Вписанные и описанные шары и сферы

Определение. Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара (рис. 206).

Рис. 206

Рис. 207

Цилиндр в таком случае называется описанным около шара. В цилиндр можно вписать шар тогда и только тогда, когда он равносторонний.

Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).

Цилиндр при этом называют вписанным в шар. Около любого цилиндра можно описать шар. Центром шара служит середина оси цилиндра, а радиус шара равен радиусу круга, описанного около осевого сечения цилиндра.

Рис. 208

Рис. 209

Определение. Шар называется описанным около конуса, если основание конуса — сечение шара, а вершина конуса принадлежит поверхности шара (рис. 208).

Конус при этом называют вписанным в шар.

Центр шара, описанного около конуса, совпадает с центром круга, описанного около осевого сечения конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

Конус при этом называют описанным около шара (рис. 209). Центр вписанного в конус шара совпадает с центром круга, вписанного в осевое сечение конуса, а радиус шара равен радиусу этого круга.

Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.

Многогранник в таком случае называют описанным около шара (рис. 210).

Не во всякий многогранник можно вписать шар. Например, вписать шар можно в любую треугольную или правильную пирамиду. А в прямую призму, в основании которой лежит прямоугольник, не являющийся квадратом, шар вписать нельзя.

Рис. 210

При нахождении радиуса r вписанного в многогранник шара (если таковой существует) удобно пользоваться соотношением

Vмногогр = •r•Sполн. поверх.

Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m•sin . Этой формулой часто пользуются при решении задач.

Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m•sin , где r — радиус шара, вписанного в многогранный угол, m — расстояние от центра шара до ребра многогранного угла, α — величина двугранного угла при этом ребре.

Если все плоские углы трёхгранного угла равны по 60°, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3r; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r. Эти соотношения часто используют при решении задач, в которых рассматриваются те или иные комбинации шаров с правильными тетраэдрами или прямоугольными параллелепипедами.

Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211). Многогранник при этом называют вписанным в шар.

Рис. 211

Не около всякого многогранника можно описать шар. Например, около любой правильной или любой треугольной пирамиды шар описать можно, а около четырёхугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом, шар описать нельзя (около ромба нельзя описать окружность). Более того, нельзя описать шар около любой наклонной призмы.

Вообще, для того чтобы около многогранника можно было описать шар, необходимо, чтобы около любой его грани можно было описать круг. При этом центр описанного шара может лежать как внутри многогранника, так и вне его или на его поверхности (даже на ребре многогранника), и проектируется в центр описанного около любой грани круга. Кроме того, перпендикуляр, опущенный из центра описанного около многогранника шара на ребро многогранника, делит это ребро (как хорду шара) пополам.

Мы уже говорили о пирамидах, все рёбра которых одинаково наклонены к основанию. Около таких пирамид всегда можно описать шар, центр которого лежит на луче, содержащем высоту пирамиды.

Высота h пирамиды, радиус Rк описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:

(R – h)2 + = R2.

Приведём формулы для вычисления радиусов вписанных и описанных шаров для правильных многогранников с ребром a.

В задачах иногда ещё рассматривают шары, касающиеся всех рёбер данного многогранника. Для куба, например, такой шар существует и его радиус равен , где a — ребро куба.

19.7. Площади поверхностей шара и его частей

Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью: она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента (сегментной поверхности).

Рис. 212

Часть шара, заключённая между двумя параллельными секущими плоскостями, называется шаровым слоем (см. рис. 212, 214). Поверхность шарового слоя называется шаровым поясом. Шаровой пояс — часть шаровой поверхности, заключённая между двумя параллельными секущими плоскостями. Перпендикуляр, проведённый из точки одного основания к плоскости другого, называется высотой шарового слоя (шарового пояса).

Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA1D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA1 — шаровой пояс.

Тело, образованное при вращении кругового сектора с углом ϕ (ϕ < 180°) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором.

Рис. 213

Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а, б) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г).

На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).

Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.

Рис. 214

Рис. 215

а) Площадь сферы. Пусть ABCDEF — правильная ломаная линия, вписанная в данную полуокружность; a — длина её апофемы (рис. 215). При вращении полуокружности вокруг её диаметра AF образуется сфера, а при вращении ломаной ABCDEF вокруг этого же диаметра AF образуется некоторая поверхность Ф.

За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n-звенной ломаной линии, вписанной в полуокружность, при n → +∞ (число сторон неограниченно возрастает).

Поверхность Ф является объединением поверхностей, образованных вращением звеньев ломаной линии, вписанной в полуокружность, вокруг её диаметра. Этими поверхностями являются боковые поверхности либо конуса (для первого и последнего звеньев ломаной), либо цилиндра (для звеньев, параллельных оси вращения; их может и не быть), либо усечённого конуса (для всех остальных звеньев ломаной).

При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь Si (i = 1, 2, …, n) поверхности, образованной вращением любого звена, равна произведению 2π, расстояния bi от середины звена до центра сферы и длины mi проекции этого звена на ось вращения, т. е. Si вращ = 2π•bi•mi.

Так как ломаная — правильная, то все bi равны апофеме an данной n-звенной ломаной, а m1 + m2 + m3 + … + mn = 2R и S1 + S2 + S3 + … + Sn = 4π•an•R. Причём an = , где pn — периметр данной ломаной. Поскольку ограниченная переменная величина при n → +∞ становится бесконечно малой, то при n → ∞ апофема an стремится к радиусу R полуокружности.

Следовательно, предел площади поверхности Ф при n → ∞ равен 4πR•R = 4πR2. Этот предел и принимается за величину площади сферы радиуса R:

Sсферы = 4πR2.

б) Площади сегментной поверхности и шарового пояса. Если правильная ломаная вписана не в полуокружность, а в некоторую её часть, например в дугу AD (см. рис. 215), при вращении которой образуется сегментная поверхность, то рассуждения, аналогичные предыдущим, приводят к выводу:

Sсегм. поверх = 2πRh,

где h — высота сферического сегмента.

Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:

Sшар. пояса = 2πRh,

где h — высота шарового пояса.

Проделайте эти рассуждения самостоятельно.

в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г).

Рассмотрим частный случай (см. рис. 213, а, б). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R, и радиусом основания (докажите это) равна πR , а площадь сегментной поверхности равна 2πRh. Значит, для площади шарового сектора справедлива формула

Sшар. сект = πR(2h + ).

 ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС, сторона которого равна 4. Известно также, что AS = BS = , a SC = 3. Найти площадь сферы, описанной около этой пирамиды.

Рис. 216

Решение. Решим эту задачу двумя методами.

Первый метод (геометрический). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС; точка Е — середина отрезка АВ (рис. 216).

Центр О сферы равноудалён от всех вершин △ АBС, поэтому принадлежит прямой, проходящей через точку D перпендикулярно плоскости АВС.

Так как точка Е — середина отрезка АВ, то SE ⟂ АВ (AS = BS) и СЕ ⟂ АВ (△ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ (CSE), поэтому (CSE) ⟂ (ABC) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.

Точка D является центром окружности, описанной около △ АВС. (По этой окружности плоскость АВС пересекает сферу, описанную около данной пирамиды.) Если L — точка пересечения прямой СЕ и упомянутой окружности, то CL — её диаметр. Найдём длину диаметра CL.

В правильном △ AВС имеем: CE = = 2; CD = СЕ = . Тогда CL = 2CD = .

Далее △ BSE (∠ BES = 90°): SE2 = SB2 – BE2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):

cos C = = = ;

△ SLC (по теореме косинусов):

SL2 = SC2 + CL2 – 2SC•CL•cos C = ⇒ SL = .

Плоскость CSL проходит через центр О сферы, следовательно, пересекает сферу по большой окружности, которая описана около △ CSL. Значит, радиус R этой окружности равен радиусу сферы, описанной около данной пирамиды. Найдём длину радиуса R.

В треугольнике CSL имеем = 2R. Так как в этом треугольнике cos C = , то sin C = = . Тогда R = = : = .

Находим площадь Q сферы:

Q = 4πR2 = 4π• = π.

Второй метод (координатный). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).

В этой системе координат вершины основания пирамиды имеют координаты: А(0; 0; 0), B(2; 2 ; 0), C(4; 0; 0).

Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = , CS = 3.

Имеем

AS2 = x2 + y2 + z2 = 19,

ВS2 = (x – 2)2 + (y – 2 )2 + z2 = 19,

CS2 = (x – 4)2 + y2 + z2 = 9.

Решая систему уравнений

x² + y² + z² = 19,(x – 2)² + (y – 2 )² + z² = 19,(x – 4)² + y² + z² = 9,

находим: х = , у = , z = .

Рис. 217

Таким образом, вершина S имеет следующие координаты:

S .

Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA2 = OB2 = OC2 = OS2 = R2. Это соотношение в координатном виде равносильно системе уравнений

a² + b² + c² = R²,(a – 2)² + (b – 2)² + c² = R², + + = R²,(a – 4)² + b² + c² = R².

Вычитая из первого уравнения четвёртое, получаем a = 2, после чего, вычитая из первого уравнения второе, получаем b = .

После вычитания третьего уравнения системы из первого её уравнения получаем:

= 0.

Подставив в это уравнение вместо a и b найденные их значения, получаем с = . Отсюда: R2 = a2 + b2 + c2 = 4 + + = . Тогда искомая площадь Q сферы равна:

Q = 4πR2 = π.

Ответ: π (кв. ед.).

19.8. Объёмы шара и его частей

Рис. 218

Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а). Объём этой фигуры равен разности объёма цилиндра с высотой 2R, радиусом основания R и удвоенного объёма конуса высоты R, радиуса основания R:

V = π•R2•2R – 2•π•R2•R = π•R3.(*)

Шар радиуса R (рис. 218, б) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2R. Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N, на рисунке не изображена.)

Будем пересекать наши фигуры плоскостями, параллельными данным плоскостям и удалёнными от центра шара на расстояние x (0 ⩽ x ⩽ R).

При х = 0 площади сечений обеих фигур равны π•R2; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π•()2 = π•(R2 – x2), а площадь сечения другой фигуры (ею является кольцо) равна π•R2 – π•x2. Следовательно, площади равноудалённых от центра шара сечений рассматриваемых фигур равны (относятся, как 1 : 1). Поэтому на основании принципа Кавальери равны и объёмы этих тел. Тогда на основании (*):

Vшара = •π•R3,

гдe R — радиус шара.

Рис. 219

Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h < R) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h, т. е.

V = π•h•R2 – π•h•(R2 + R•(R – h) + (R – h)2) =

= π•h2•(3R – h).

При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2R – h (рис. 220): V = π•R3 – •π•(2R – h)2•(3R – (2R – h)) = π•h2(3R – h), т. е. получаем ту же самую формулу. Подставляя в эту формулу h = R, получим V = π•R2(3R – R) = π•R3, что соответствует объёму полушара.

Рис. 220

Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:

Vшар. сегм = π•h2•(3R – h),

или в другом виде

Vшар. сегм = π•h2•.

Рис. 221

Рис. 222

Рис. 223

Выведем теперь формулу для вычисления объёма шарового сектора.

Сначала рассмотрим шаровой сектор, состоящий из шарового сегмента высоты h и конуса высоты (R – h) с вершиной в центре шара радиуса R (рис. 221). Для него имеем:

Vшар. сект = Vсегм + Vкон = π•h2•(3R – h) +

+ π•(R – h•R2 – (R – h)2) = •π•R2•h.

Докажите самостоятельно, что и для других шаровых секторов (рис. 222, 223) их объём вычисляется по формуле:

Vшар. сект = π•R2•h.

Отметим, что объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле

Vшар. слоя = (3 + 3 + H2).

 ЗАДАЧА (3.457). Четыре шара радиуса R и четыре шара радиуса r расположены так, что каждый касается трёх шаров одного радиуса и трёх шаров другого радиуса. Найти отношение объёма шара радиуса R к объёму шара радиуса r (R > r).

Решение. Обозначим V1, V2 — объёмы шаров с радиусами соответственно R и r. Тогда V1 = πR3, V2 = πr 3, значит, = .

Пусть А, В, С, Р — центры шаров радиуса R; A1, B1, С1, P1 — центры шаров радиуса r. Тогда:

1) AB = BC = CA = AP = BP = CP = 2R ⇒ РАВС — правильный тетраэдр с ребром 2R;

2) A1B1 = B1C1 = C1A1 = A1P1 = B1P1 = C1P1 = 2r ⇒ Р1А1В1С1 — правильный тетраэдр с ребром 2r.

Рис. 224

Обозначим точки A2, B2, C2, P2 — центры граней тетраэдра РАВС (рис. 224) и докажем, что все четыре высоты АA2, BB2, CC2, PP2 пересекаются в одной точке и делятся этой точкой в отношении 3 : 1, считая от вершин.

В самом деле, если М = AА2 ∩ PP2, то из подобия треугольников НАР и НР2А2 следует HP : НA2 = AP : A2P2 = 3 : 1, тогда из подобия треугольников APM и A2P2M следует, что AP : A2P2 = PM : MP2 = AM : MA2 = 3 : 1, т. е. PM = PP2.

Аналогично доказывается, что высоты BB2 и CC2 делятся точкой M в отношении BM : MB2 = CM : MC2 = 3 : 1 и, таким образом, точки A2, B2, C2, P2 равноудалены от точки М.

Далее, так как шар с центром P1 и радиусом r касается шаров с центрами А, В, C и радиусами R, то P1А = P1B = P1С = R + r, т. е. точка P1 равноудалена от вершин А, В и С правильного тетраэдра РАВС. Так как (R + r) < 2R, то P1 принадлежит высоте РP2 этого тетраэдра: P1 ∈ PP2. Аналогично доказывается, что A1 ∈ АA2, B1 ∈ ВB2, C1 ∈ СC2.

Найдём дважды длину высоты РP2 тетраэдра РАВС: с одной стороны, как длину катета прямоугольного треугольника АPP2, с другой стороны, как сумму длин отрезков РМ, МР1 и P1P2.

В правильном △ AВС со стороной 2R имеем:

AP2 = AH = • = .

Тогда в прямоугольном △ AРP2 :

РР2 = = = .

Найдём длину отрезка PP2 иначе. В прямоугольном △ AP1P2 имеем:

Аналогично можно убедиться, что A1A2 = B1B2 = C1C2 = P1P2 = . Тогда, учитывая, что МА2 = МB2 = МC2 = MP2, приходим к выводу: MA1 = MB1 = MC1 = MP1. Это означает, что точка M — общий центр правильных тетраэдров РАВС и Р1А1B1C1 и РP2 = РM + МP1 + P1P2.

Так как в правильном тетраэдре РАВС с ребром 2R для расстояния РМ от вершины Р до центра М этого тетраэдра выполняется РМ = РР2 = • = , то в правильном тетраэдре P1A1B1C1 с ребром 2r для расстояния P1M от вершины P1 до его центра М выполняется Р1M = .

Подставляя в равенство PP2 = РM + MP1 + P1P2 найденные значения длин отрезков РР2, РM, МP1 и P1P2, получаем:

= + + ,

или после элементарных преобразований:

R2 – 6Rr + r2 = 0.

Разделив это уравнение на r2 и введя новую переменную t = , получаем уравнение t2 – 6t + 1 = 0, корнями которого являются t1 = 3 – 2 , t2 = 3 + 2 . Так как t1 < 0, то условию задачи удовлетворяет лишь значение t2 = 3 + 2 . Это означает, что = 3 + 2 . Тогда = = (3 + 2 )3.

Ответ: (3 + 2 )3.

Задания для работы с интернет-ресурсами

1. Посмотрите в Интернете и отберите рисунки по темам: «Тело вращения», «Поверхность вращения». Они помогут вам при построении рисунков к решению задач.

2. Сравните материалы Интернета и учебника по темам: «Цилиндр», «Конус», «Цилиндрическая и коническая поверхности вращения», «Касательная плоскость к цилиндру и конусу», «Формулы для вычисления площадей боковой и полной поверхностей цилиндра и конуса», «Формулы для вычисления объёма цилиндра и конуса», «Развёртки цилиндра и конуса», «Модели цилиндра и конуса». Что нового вы узнали из Интернета?

3. Вы узнаете много нового и интересного о замечательных кривых, сделав запрос в Интернете по темам: «Сечения цилиндра и конуса плоскостью», «Кривые второго порядка», «Конические сечения».

4. Найдите рисунки по темам: «Призма, вписанная в цилиндр и описанная около цилиндра», «Пирамиды, вписанные в конус и описанные около конуса». Удачные рисунки скопируйте в «Избранное» или в «Картотеку», чтобы можно было ими пользоваться при решении задач.

5. Найдите в Интернете теоремы о параллельных сечениях конуса. Посмотрите рисунки усечённых конусов. Найдите формулы для вычисления площадей боковой и полной поверхностей усечённого конуса и его объёма.

6. В Интернете посмотрите материал по темам: «Сфера», «Шар», «Изображение сферы», «Уравнение сферы», «Взаимное расположение сферы и плоскости», «Пересечение шара и сферы с плоскостью», «Плоскость, касательная к сфере и шару», «Шаровой сегмент, его основание и высота; сегментная поверхность», «Шаровой слой, его основания и высота», «Шаровой пояс», «Шаровой сектор и его поверхность».

7. Найдите в Интернете формулы для вычисления площадей сферы, сегментной поверхности, шарового пояса, поверхности шарового сектора, объёмов шара, шарового сегмента, шарового сектора, шарового слоя.

8. Обратите особое внимание на материал: «Шары и сферы, вписанные в двугранный угол и многогранный угол», «Шары и сферы, вписанные в многогранники (особенно в правильные многогранники) и описанные около них», «Шары и сферы, вписанные в цилиндр, конус и описанные около них».

9. Посмотрите рисунки и материалы по темам: «Комбинации геометрических тел», «Комбинации геометрических фигур в окружающем нас мире, в архитектуре». Тем, кто интересуется черчением и графикой, предлагаем найти статьи: «Техническое черчение: цилиндр и конус», «Пересечение двух цилиндров с перпендикулярными осями», «Резьбы и резьбовые соединения», «Цилиндрическая винтовая линия».

Вопросы для самооценки

1. Оцените результаты изучения этой главы. Довольны ли вы ими?

2.Что нового вы узнали в этой главе?

3.Как могут пригодиться вам эти знания в повседневной жизни?

4.Какие задания в этой главе были для вас самыми трудными? Почему?

5.Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?

6.Обращались ли вы за помощью к одноклассникам, родителям, учителю?

Источник

Геометрия

План урока:

Понятие сферы и шара

Люди постоянно сталкиваются с предметами, имеющими форму шара. В большинстве спортивных игр (баскетболе, большом и настольном теннисе, футболе) используются мячи, которые по форме как раз являются шарами. Такую же форму имеют многие фрукты – яблоки, апельсины, мандарины. Более того, известно, что Земля, другие планеты и звезды, большинство крупных спутников также представляют собой шары.

Важно отличать шар от сферы. Сферой называют только поверхность шара. Сам же шар является объемной фигурой, к нему относят всю часть пространства, ограниченную сферой.

Дадим строгие определения сферы и шара:

Отрезок, соединяющий точку на сфере с ее центром, именуется радиусом сферы. Он же называется и радиусом шара, заключенного внутри этой сферы.

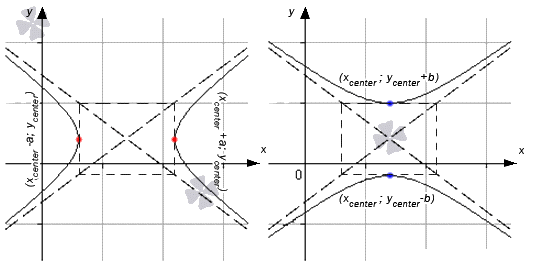
Проходящий через центр сферы отрезок, чьи концы принадлежат сфере, именуется диаметром сферы. Сама сфера считается частью шара, также как и окружность считается частью круга.Показывают шар или сферу на рисунке так:

Из определения сферы явно вытекает тот факт, что все ее радиусы одинаковы. Это в свою очередь означает, что центр сферы – это середина диаметра, и диаметр вдвое длиннее радиуса.

Заметим, что сфера является телом вращения. Она получается при повороте полуокружности вокруг ее диаметра:

Уравнение сферы

В планиметрии мы уже изучали уравнения линии. Так назывались ур-ния с двумя переменными, каждое решение которых соответствовало точке на координатной плос-ти, принадлежавшей заданной линии. Если же точка не принадлежала линии, то ее координаты решением соответствующего ур-ния не являлись. В частности, нам удалось получить уравнения прямой и окружности.

Аналогично в стереометрии вводится понятие уравнения поверхности. Так как в пространстве используются уже три координаты (х, у и z), то ур-ния поверхности содержат три переменных. Координаты всякой точки, принадлежащей поверхности, будут являться решениями ур-ния этой поверхности. И наоборот, координаты точки, не принадлежащей поверхности, будут обращать ур-ние поверхности в неверное равенство.

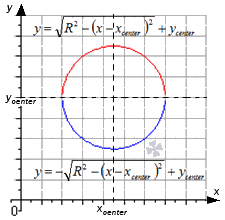
Выведем ур-ние сферы. Пусть ее центр располагается в точке С с координатами (х₀, у₀, z₀), а радиус обозначен как R. Возьмем произвольную точку А на сфере. По определению сферы расстояние между А и С должно составлять R:

Точки, координаты которых удовлетворяют этому неравенству, находятся от центра сферы на расстоянии меньше ее радиуса. Это значит, что они находятся внутри сферы, то есть принадлежат шару, чьей поверхностью является рассматриваемая сфера. Если же координаты точки удовлетворяют неравенству

то можно утверждать, что точка находится вне пределов сферы, то есть она не принадлежит ни сфере, ни шару.

Задание. Напишите уравнение сферы, центр которой располагается в точке (2; – 4; 7) и чей радиус равен 3.

Решение. Здесь мы просто подставляем координаты центра сферы и ее радиус в ур-ние сферы:

Задание. Есть сфера с радиусом 9, чей центр располагается в точке О(2; 3; 4). Определите, какие из следующих точек будут принадлежать этой сфере: А(1; 7; – 4), В(0; 6; 10), С(– 2; – 1; 11), D(5; 6; 8).

Решение. Сначала составляем уравнение сферы, описанной в условии:

Равенство неверное, значит, В не располагается на сфере (более того, раз 49 2 .

Задание. Некоторое тело представляет собой шар, внутри которого есть полость, также имеющая форму шара, причем центры этих шаров совпадают. Докажите, что площадь сечения этого тела, проходящего через центр шаров, совпадает с площадью сечения, являющегося касательной к внутреннему шару.

Решение. Обозначим радиус большей сферы как R, а радиус меньшей (внутренней сферы) как r. Площадь центрального сечения в виде кольца (показано синим цветом) представляет собой разницу между площадью большого круга с радиусом R и малого с радиусом r:

Задание. Сфера радиусом 5 см касается каждой стороны треугольника со сторонами 13, 14 и 15 см. Каково расстояние между центром этой сферы и плос-тью треугольника?

Решение. Обозначим вершины треугольника точками А, В и С. Пусть

Заметим, что плос-ть АВС – секущая, а само сечение имеет форму окруж-ти. Эта окруж-ть будет касаться сторон ∆АВС, то есть она является вписанной окруж-тью. Как вычислить ее радиус НK?

Площадь ∆АВС можно найти по формуле Герона. Предварительно найдем полупериметр ∆АВС:

Пересечение двух сфер

Пусть есть две пересекающиеся сферы с центрами в точках О₁ и О₂ с радиусами R₁ и R₂ соответственно. Какую форму будет иметь линия L, по которой они пересекаются?

Эта линия является множеством точек, которые принадлежат как первой, так и второй сфере. Обозначим две произвольные точки этой линии буквами А и В:

Проведем радиусы О₁А, О₁В, О₂А и О₂В. Теперь сравним ∆АО₁О₂ и ∆ВО₁О₂. Сторона О₁О₂ у них общая, а другие стороны попарно равны как радиусы сфер:

Получается, что ∆АО₁О₂ и ∆ВО₁О₂ равны. Теперь из точек А и В опустим высоты на прямую О₁О₂. Из равенства ∆АО₁О₂ и ∆ВО₁О₂ вытекает два факта:

эти высоты упадут в одну точку Н;
эти высоты будут одинаковы, то есть АН = НВ.

Другими словами, А и В равноудалены от Н. Получается, что точки А и В находятся на окруж-ти, центр которой – точка Н. Заметим, что О₁О₂ – перпендикуляр к плоскости окружности, ведь О₁О₂⊥АН и О₁О₂⊥ВН.

Точки А и В были выбраны произвольно, поэтому можно утверждать, что любые точки линии L будут находиться на одной окруж-ти. Докажем и обратное утверждение – любая точка, лежащая на этой окруж-ти, будет принадлежать линии L. Возьмем на окруж-ти какую-нибудь точку С и построим радиус НС:

Теперь сравним ∆О₁НС и ∆О₁НА. Они прямоугольные, ведь О₁Н – перпендикуляр к плос-ти окружности. Катет О₁Н у них общий, а катеты АН и НС одинаковы как радиусы окруж-ти. Значит, ∆О₁НС и ∆О₁НА равны, и потому

Это равенство означает, что С принадлежит сфере с центром в О₁. Аналогично рассмотрев ∆О₂НС и ∆О₂НА, можно показать, что С также принадлежит и второй сфере. Тогда С принадлежит пересечению этих сфер.

Итак, всякая точка линии L лежит на окруж-ти с центром Н, и наоборот, каждая точка этой окруж-ти лежит на линии L. Это означает, что L как раз и является этой окружностью.

Отметим ещё один факт: по неравенству треугольника отрезок О₁О₂ должен быть меньше суммы отрезков О₁А и О₂А, то есть суммы радиусов сфер.

Задание. Сферы имеют радиусы 25 см и 29 см, а расстояние между их центрами составляет 36 см. Вычислите радиус окруж-ти, по которой они пересекаются.

Решение. Пусть А – одна их точек сечения. Искомый радиус обозначим как АН. В итоге получим такую картинку:

Площадь сферы

Сферическая поверхность, как и всякая другая ограниченная поверхность, имеет какую-то площадь. Напомним, что для вычисления площадей цилиндрической и конической поверхности мы строили их плоские развертки и находили площади уже этих разверток, используя формулы из планиметрии. Оказывается, что для сферы построить такую развертку невозможно. Мы не будем доказывать строго этот факт, но он известен из географии – любая карта Земли, которая как раз и должна быть разверткой сферической поверхности нашей планеты, является неточной и сильно искажает форму и размеры континентов. Если бы существовал способ построить точную развертку, то и географические карты не имели бы таких искажений.

Однако вычислить площадь сферы всё же можно по известной формуле:

Сейчас мы не будем доказывать эту формулу. Отметим лишь, что для ее получения необходимо использовать интегралы.

Задание. Какова площадь сферы с радиусом 5 см?

Решение. Просто используем формулу:

Ответ: 100π см 2 .

Вписанные и описанные сферы

Если каждая точка многогранника лежит на поверхности сферы, то говорят, что многогранник вписан в сферу. Тогда сферу именуют описанной, а многогранник – вписанным.

Если же сфера касается каждой грани многогранника, то уже наоборот, сфера вписана в многогранник. Тогда уже сфера будет вписанной фигурой, а многогранник – описанной.

Заметим, что не в каждый многогранник может быть вписанным или описанным. Например, в куб вписать сферу можно, а в прямоугольный параллелепипед, измерения которого отличаются, уже вписать сферу не получится.

Надо отметить, что в сферу можно вписать не только в многогранник, но и другие геометрические фигуры, в частности конус и цилиндр. Здесь нужно уточнить (без доказательства), что если касание плос-ти и сферы происходит только в одной точке, то цилиндрическая и коническая поверхности касаются сферы уже по окруж-ти.

Задание. Правильная пирамида вписана в сферу. Докажите, высота этой пирамиды проходит через центр сферы.

Решение. Опустим из центра сферы О перпендикуляр ОН на основание пирамиды. Далее возьмем произвольную вершину Х основания пирамиды, и соединим ее с Н отрезком ХН. По теореме Пифагора можно вычислить длину ХН (радиус сферы ОХ обозначим, буквой R):

Получилось, что расстояние ХН не зависит от самой точки Х. То есть все вершины основания равноудалены от точки, то есть Н – центр описанной около основания окруж-ти. Это означает, что перпендикуляр ОН одновременно является высотой правильной пирамиды, ч. т. д.

Задание. Вычислите радиус описанной сферы, в которую вписан правильный тетраэдр со стороной а.

Решение. Правильный тетраэдр можно считать правильной треугольной пирамидой, поэтому (согласно предыдущей задаче) из центра сферы О можно опустить перпендикуляр на основание АВС, который упадет в точку Н – центр основания. Так как тетраэдр правильный, то ∆АВС – равносторонний, то есть Н – эта точка пересечения и медиан, и высот. Опустим из А высоту АК, она пройдет через Н. Так как АК – ещё и медиана, то

Далее найдем длину АН. Вспомним, что АН – медиана, а точка пересечения медиан Н делит их в отношении 2:1. Это значит, что

Буквой R здесь обозначен радиус описанной сферы. Осталось применить теорему Пифагора к ∆АНD:

Задание. Докажите что вокруг любого тетраэдра можно описать сферу.

Решение. Обозначим вершины произвольного тетраэдра буквами А, В, С и D. Далее на грани АВС отметим точку К – центр окруж-ти, описанной около ∆АВС. Аналогично на грани АВD отметим Н – центр окруж-ти, описанной около ∆АВD:

Напомним, что центры описанных окружностей располагаются в той точке, где пересекаются серединные перпендикуляры. Это значит, что если мы из К и Н опустим перпендикуляры на ребро АВ, то эти перпендикуляры будут серединными, то есть они попадут в одну точку М, являющуюся серединой ребра АВ.

Мы получили плос-ть НМК. Заметим, что НМК⊥АВ по признаку перпендикулярности прямой и плоскости, так как АВ⊥МН и АВ⊥МК. Но тогда АВС⊥МНК уже по признаку перпендикулярности плоскостей, ведь АВС проходит через АВ, являющийся перпендикуляром к НМК. По той же причине и АВD⊥НМК.

Далее проведем через К перпендикуляр m к АВС. Он должен будет принадлежать НМК, ведь НМК⊥АВD. Аналогично и через Н проведем перпендикуляр n к АВD, который также будет принадлежать НМК.

В плос-ти НМК есть две прямые, mи n. Они либо параллельны, либо пересекаются. Но перпендикуляры к двум плос-тям могут быть параллельны только в случае, если сами эти плос-ти параллельны (или совпадают). Но АВС и АВD непараллельны и не совпадают, поэтому m и n непаралелльны, то есть они пересекаются в какой-то точке О.

Покажем, что точка О равноудалена от всех вершин тетраэдра. Сравним ∆АОК и ∆СОК. Они прямоугольные, ведь ОК – перпендикуляр к АВС. ОК – общий катет, а катеты АК и СК одинаковы как радиусы описанной окруж-ти. Значит, ∆АОК и ∆СОК равны, ОА = ОС. Аналогично рассмотрев ∆АОК и ∆ВОК, приходим к выводу, что ОА = ОВ. Далее рассматриваем ∆ОНD и ∆ОНА и получаем, что ОА = ОD. Эти три равенства все вместе означают, что О равноудалена от точек А, В, С и D. А это значит, что на сфере с центром О и радиусом ОА будут лежать все вершины тетраэдра, то есть такая сфера окажется описанной, ч. т. д.

Примечание. Несложно доказать, что описанная сфера будет единственной. Действительно, если бы около тетраэдра можно было описать две различных сферы, то они пересекались бы в точках А, В, С и D. Сферы пересекаются по окруж-ти, то есть А, В, С и D должны лежать на одной окруж-ти, но это невозможно, ведь они не располагаются в одной плос-ти. Значит, двух описанных сфер существовать не может.

Доказанное в задаче утверждение можно сформулировать несколько иначе:

Сегодня мы изучили сферу – одну из важнейших геометрических фигур. Именно сферическую форму имеют звезды и планеты. Жидкость, оказавшаяся в невесомости, также принимает форму шара. Важно запомнить, что сечение сферы имеет форму окруж-ти, и касательные к сфере обладают почти такими ми же свойствами, как и касательные к окруж-ти в планиметрии.

Уравнение касательной к сфере в точке

19.1. Определения шара, сферы и их элементов

С шаром и сферой мы уже знакомы. Напомним их определения.

Определение. Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R ( R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара .

На рисунке 193 изображён шар с центром О и радиусом R = OА.

Из определений шара и сферы следует, что шар с центром О и радиусом R является объединением двух множеств точек: 1) множества точек M пространства, для которых OM (они называются внутренними точками шара и образуют его внутренность); 2) множества всех М, для которых ОМ = R (эти точки являются граничными точками шара, а их объединение составляет границу шара, которая называется шаровой поверхностью и является сферой c центром О и радиусом R ) .

Радиусом шара называют также всякий отрезок, соединяющий центр шара с точкой шаровой поверхности. Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара . Концы любого диаметра шара называются диаметрально nротивоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара ( сферы ) . На рисунке 193 отрезки ОА, ОВ, ON, OS — радиусы шара; отрезки АВ , NS — диаметры шара; A и B — диаметрально противоположные точки шара. Из определения диаметра шара следует, что он равен удвоенному радиусу шара.

Покажем, что шар — тело вращения. Для этого рассмотрим полукруг F с центром О и радиусом R (рис. 194, а ). При вращении полукруга F вокруг прямой, содержащей его диаметр NS, образуется некоторое тело F 1 (рис. 194, б ). Так как вращение вокруг прямой — движение и точка О принадлежит оси l вращения, то каждая точка тела F 1 удалена от точки O на расстояние, не большее R (движение сохраняет расстояния между точками). Это означает, что тело F 1 есть шар с центром О и радиусом R. Кроме того, при вращении границы полукруга — полуокружности — вокруг прямой l образуется сфера. Прямая, содержащая любой диаметр шара, может быть рассмотрена как ось вращения. Следовательно, сечением шара плоскостью, перпендикулярной его оси вращения l и пересекающей шар, является круг, а сечением сферы такой плоскостью — окружность этого круга; центр круга (окружности) есть точка пересечения секущей плоскости с осью l.

Плоскость, проходящая через центр шара (сферы), называется диаметральной плоскостью шара ( сферы ) . Сечением шара диаметральной плоскостью является круг, радиус которого равен радиусу шара. Такой круг называется большим кругом, а его окружность — большой окружностью ; большая окружность является пересечением сферы и её диаметральной плоскости.

19.2. Изображение сферы

Рассмотрим сферу, диаметр NS которой проведён вертикально (рис. 195, а ). Большая окружность, по которой сферу пересекает диаметральная плоскость, перпендикулярная диаметру (оси) NS, называется экватором , а точки N и S — полюсами сферы . Окружность, ограничивающая круг — изображение сферы, — называется абрисом или очерковой линией .

Типичная ошибка (!) при изображении сферы (рис. 195, б ) в том, что, изображая её экватор эллипсом, полюсы изображают расположенными на абрисе.

Для верного и наглядного изображения сферы вспомним, как в курсе черчения изображают фигуру на комплексном двухкартинном чертеже (эпюре) посредством ортогонального её проектирования на две взаимно перпендикулярные плоскости, одну из которых называют фронтальной (обозначают V ) , а другую — профильной (обозначают W ) плоскостями проекций.

Сферу расположим так, чтобы её ось N ′ S ′ была параллельна профильной ( W ), но не параллельна фронтальной ( V ) плоскостям проекций. Тогда ортогональные проекции сферы на плоскости V и W имеют вид, изображённый на рисунке 196. На нём: равные круги — проекции сферы на плоскости V и W ; отрезки A 1 B 1 и N 1 S 1 — профильные проекции соответственно экватора и оси сферы; точки N, S — фронтальные проекции полюсов (строятся с помощью линий связи); точки А, В — фронтальные проекции концов диаметра экватора, параллельного фронтальной плоскости (строятся с помощью линий связи); отрезок CD — фронтальная проекция диаметра C ′ D ′ сферы, перпендикулярного профильной плоскости; эллипс с осями АВ и CD — фронтальная проекция экватора. При таком расположении относительно плоскостей проекций сфера изображается так, как показано на рисунках 195, a ; 196, a.

Действительно, из равенства △ ОBF = △ ЕNО (см. рис. 196, а ) следует: OВ = EN, BF = NO. Это означает: а) если изображены полюсы N и S сферы, то вершины А и В эллипса — изображения экватора определяются из равенств OВ = ОА = NE, где NE || OD ; б) если изображён экватор (т. е. дана малая ось AB эллипса-экватора), то положение полюсов N и S определяется из равенств ON = OS = BF, где BF || OD.

 ЗАДАЧА (3.106). Найти в пространстве множество вершин всех прямых углов, опирающихся на данный отрезок АВ.

Решени е. Если ∠ АМВ = 90 ° , то точка М принадлежит окружности с диаметром АВ (рис. 198, a ).

Проведём произвольную плоскость α , содержащую отрезок АВ. В этой плоскости множество всех точек М, из которых отрезок AB виден под прямым углом, есть окружность, для которой отрезок AB — диаметр. Точки А и В этому множеству точек не принадлежат. (Почему?) Таким образом, искомое множество вершин прямых углов, опирающихся на отрезок AB , есть сфера с диаметром AB . Точки А и В этому множеству точек-вершин не принадлежат.

19.3. Уравнение сферы

Составим уравнение сферы с центром А ( a ; b ; с ) и радиусом R в декартовой прямоугольной системе координат Oxyz.

Пусть М ( x ; у ; z ) — любая точка этой сферы (рис. 199). Тогда MA = R или MA 2 = R 2 . Учитывая, что MA 2 = ( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 , получаем искомое уравнение cферы

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 .

Если начало системы координат совпадает с центром A сферы, то a = b = c = 0 , а сфера в такой системе координат имеет уравнение

x 2 + y 2 + z 2 = R 2 .

Из полученных уравнений следует, что сфера — поверхность второго порядка.

Так как для любой точки М ( х ; у ; z ) шара с центром А ( a ; b ; с ) и радиусом R выполняется МА ⩽ R, то этот шар может быть задан неравенством

( x – a ) 2 + ( у – b ) 2 + ( z – c ) 2 ⩽ R 2 .

При этом для всех внутренних точек М шара выполняется условие МА 2 R 2 , т. е.

( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 R 2 ,

для точек М шаровой поверхности — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 = R 2 ,

для точек М вне шара — условие

т. е. ( х – a ) 2 + ( у – b ) 2 + ( z – c ) 2 > R 2 .

19.4. Пересечение шара и сферы с плоскостью

Рассмотрим подробнее вопрос о пересечении шара и сферы с плоскостью. Имеет место следующая теорема.

Теорема 30 (о пересечении шара и сферы с плоскостью ) . 1) Если расстояние от центра шара до данной плоскости меньше радиуса шара, то пересечением шара с плоскостью является круг. Центром этого круга является основание перпендикуляра, проведённого из центра шара на плоскость, или сам центр шара, если плоскость проходит через этот центр. Пересечением сферы с плоскостью является окружность указанного круга. Радиус r сечения в этом случае равен r = , где R — радиус шара, a d — расстояние от центра шара до плоскости сечения. 2) Если расстояние от центра шара до данной плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку. 3) Если расстояние от центра шара до данной плоскости больше радиуса, то плоскость не имеет с шаром общих точек.

Доказательств о. Пусть точка О — центр шара, R — его радиус; α — данная плоскость, точка A — основание перпендикуляра, проведённого из центра O на плоскость α . Обозначим ρ ( О ; α ) = | ОА | = d — расстояние от центра шара до плоскости α .

Рассмотрим каждый из случаев взаимного расположения шара и данной плоскости α .

1) ρ ( O ; α ) = d R и плоскость α не проходит через центр О шара (рис. 200). Докажем, что пересечение шара и плоскости есть круг с центром А и радиусом r = . Для этого достаточно убедиться, что любая точка пересечения шара и плоскости α есть точка круга с центром А и радиусом r = и, обратно, любая точка этого круга есть точка указанного пересечения.

Действительно, пусть М — произвольная точка шара, принадлежащая плоскости α (см. рис. 200). В прямоугольном треугольнике AOM по теореме Пифагора ОM 2 = ОА 2 + АМ 2 , откуда AM = . Так как точка М принадлежит шару, то ОМ ⩽ R, тогда OM 2 – OA 2 ⩽ R 2 – d 2 , поэтому АМ ⩽ . Это означает, что точка М сечения шара плоскостью α находится от точки А на расстоянии, не большем , следовательно, она принадлежит кругу с центром А и радиусом .

Обратно, пусть М — произвольная точка плоскости α , принадлежащая кругу с центром А и радиусом r = . В прямоугольном треугольнике AOM по теореме Пифагора OM 2 = ОA 2 + AM 2 . Так как AM ⩽ r , то OM 2 ⩽ OA 2 + r 2 = d 2 + R 2 – d 2 = R 2 , откуда OM ⩽ R . Значит, точка М принадлежит данному шару. Учитывая, что точка М принадлежит и плоскости α , приходим к выводу: точка M принадлежит пересечению данного шара и плоскости α .

Если неравенства, которые использовались в предыдущем доказательстве, заменить равенствами, то, рассуждая аналогично, можно доказать, что при d R пересечением сферы и плоскости является окружность с центром А и радиусом r = . Проделайте это самостоятельно.

2) ρ ( O ; α ) = d = OA = R (рис. 201).

Так как ОА = ρ ( O ; α ) = R, то точка А, являющаяся основанием перпендикуляра из центра О шара на плоскость α , принадлежит шаровой поверхности, ограничивающей данный шар.

Пусть M — произвольная точка плоскости α , отличная от точки A (см. рис. 201). Тогда длины наклонной ОМ и перпендикуляра OA, проведённых из точки О к плоскости α , удовлетворяют неравенству OM > ОА = R. Значит, точка М не принадлежит шару. Следовательно, плоскость α имеет только одну общую точку с шаром — точку А.

3) ρ ( О ; α ) = ОА = d > R (рис. 202). Для любой точки М плоскости α выполняется (почему?) ОМ ⩾ d > R. Это означает, что на плоскости α нет точек шара. Теорема доказана. ▼

Решени е. а) Пусть точка O — центр шара, OD — его радиус, точка С — середина радиуса OD ; α — секущая плоскость, проходящая через точку С перпендикулярно OD.

АС = r = , где r — радиус сечения шара плоскостью α . Тогда площадь этого сечения равна π r 2 = .

б) Найдём площадь поверхности конуса с вершиной О и радиусом основания r = .

π r • R = π • • R = ,

а площадь его полной поверхности — + = π R 2 • (2 + ).

Площадь боковой поверхности пирамиды равна 3 S △ EOF = EF • ОН, где OH — апофема пирамиды. В прямоугольном треугольнике OHF находим

ОН = = = .

Тогда EF • OH = — площадь боковой поверхности пирамиды.

Следовательно, площадь полной поверхности пирамиды равна

+ = R 2 ( + ).

Ответ: a) ; б) π R 2 (2 + ); в) ; R 2 ( + ).

19.5. Плоскость, касательная к сфере и шару

Из теоремы 30 следует, что плоскость может иметь со сферой (с шаром) только одну общую точку.

Также говорят, что плоскость касается сферы (шара) .

Любая прямая, лежащая в касательной плоскости к сфере и проходящая через точку их касания, называется касательной прямой к сфере ; эта прямая имеет со сферой единственную общую точку — точку касания, и радиус сферы, проведённый в точку касания, перпендикулярен касательной прямой.

Заметим, что если прямая a касается сферы в точке М , то эта прямая касается в точке М той окружности большого круга, которая является сечением сферы и диаметральной плоскости, проходящей через прямую a.

Справедливо и обратное: если прямая a касается окружности большого круга сферы в точке М , то эта прямая касается в точке М самой сферы.

Более того, так как прямая a, касающаяся сферы в точке М , имеет со сферой лишь одну общую точку — точку М , то эта прямая касается любой окружности, по которой пересекаются данная сфера и любая (не только диаметральная) плоскость, проходящая через прямую a. А поскольку радиус, проведённый в точку касания прямой и окружности, перпендикулярен касательной прямой, то центры всех этих окружностей — полученных сечений сферы — лежат в плоскости, проходящей через точку М перпендикулярно касательной прямой a. При этом, если точка О — центр данной сферы радиуса R , точка А — центр окружности радиуса r , по которой пересекает сферу одна (любая) из плоскостей, проходящих через касательную в точке М прямую к данной сфере, ϕ — величина угла между этой секущей плоскостью и проходящей через точку М диаметральной плоскостью данной сферы, то справедливо равенство r = R • cos ϕ ( △ ОАМ — прямоугольный, так как отрезок ОА перпендикулярен секущей плоскости (почему?)).

Теорема 31. Если плоскость касается сферы, то она перпендикулярна радиусу, проведённому в точку касания.

Доказательств о. Пусть дана сфера с центром O и радиусом R. Рассмотрим плоскость α , касающуюся данной сферы в точке M (см. рис. 205) и докажем, что ОM ⟂ α .

Предположим, что радиус ОM — не перпендикуляр, а наклонная к плоскости α . Значит, расстояние от центра сферы до плоскости α , равное длине перпендикуляра, проведённого из центра О на плоскость α , меньше радиуса. Тогда по теореме 30 плоскость α пересекает сферу по окружности. Но по условию теоремы плоскость α касается сферы и имеет с ней единственную общую точку M. Пришли к противоречию, которое и доказывает, что OM ⟂ α . Теорема доказана. ▼

Справедлива обратная теорема.

Доказательств о. Пусть плоскость α проходит через точку M сферы и перпендикулярна радиусу ОM (см. рис. 205). Значит, расстояние от центра сферы до плоскости равно радиусу ОM. Тогда по теореме 30 плоскость α и сфера имеют единственную общую точку M, следовательно, плоскость α касается сферы (в точке M ). Теорема доказана. ▼

— диаметр шара, делящий его хорду пополам, перпендикулярен этой хорде;

— отрезки всех касательных прямых, проведённых к шару из одной расположенной вне шара точки, равны между собой (они образуют поверхность конуса с вершиной в данной точке, а точки касания этих прямых — окружность основания этого конуса);

— произведение длин отрезков хорд шара, проходящих через одну и ту же внутреннюю точку шара, есть величина постоянная (равная R 2 – a 2 , где R — радиус шара, a — расстояние от центра шара до данной точки);

— если из одной и той же точки вне шара проведены к нему секущая и касательная, то произведение длины отрезка всей секущей на длину отрезка её внешней части равно квадрату длины отрезка касательной (и равно a 2 – R 2 , где R — радиус шара, a — расстояние от центра шара до данной точки).

19.6. Вписанные и описанные шары и сферы

Определение. Шар называется описанным около цилиндра, если основания цилиндра служат сечениями шара (рис. 207).

Конус при этом называют вписанным в шар.

Определение. Шар называется вписанным в конус, если основание и все образующие конуса касаются шара.

Определение. Шар называется вписанным в многогранник, если он касается всех граней многогранника.

Многогранник в таком случае называют описанным около шара (рис. 210).

V многогр = • r • S полн. поверх .

Шар называется вписанным в двугранный угол, если он касается его граней. Центр вписанного в двугранный угол шара лежит на биссекторной плоскости этого двугранного угла. При этом для радиуса r шара, вписанного в двугранный угол, величины α этого угла и расстояния m от центра шара до ребра двугранного угла справедлива формула: r = m • sin . Этой формулой часто пользуются при решении задач.

Шар называется вписанным в многогранный угол, если он касается всех граней многогранного угла. При решении задач, в которых рассматриваются вписанные в многогранный угол шары, удобно пользоваться соотношением: r = m • sin , где r — радиус шара, вписанного в многогранный угол, m — расстояние от центра шара до ребра многогранного угла, α — величина двугранного угла при этом ребре.

Если все плоские углы трёхгранного угла равны по 60 ° , то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно 3 r ; если все плоские углы трёхгранного угла прямые, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса r равно r . Эти соотношения часто используют при решении задач, в которых рассматриваются те или иные комбинации шаров с правильными тетраэдрами или прямоугольными параллелепипедами.

Определение. Шар называется описанным около многогранника, если все вершины многогранника принадлежат поверхности шара (рис. 211) . Многогранник при этом называют вписанным в шар.

Высота h пирамиды, радиус R к описанного около основания пирамиды круга и радиус R описанного около этой пирамиды шара связаны соотношением:

( R – h ) 2 + = R 2 .

19.7. Площади поверхностей шара и его частей

Часть шара, заключённая между секущей плоскостью и одной из двух частей его сферической поверхности, называется шаровым сегментом (рис. 212 и 214). Поверхность шарового сегмента называется сегментной поверхностью : она представляет собой часть шаровой поверхности, отсекаемую какой-нибудь плоскостью. Круг АВ, по которому плоскость пересекает шар, называется основанием шарового сегмента, а окружность этого круга — основанием сегментной поверхности. Отрезок ОС радиуса, перпендикулярного секущей плоскости, называется высотой шарового сегмента ( сегментной поверхности ) .

Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности CAA 1 D (см. рис. 212) вокруг диаметра CD образуется шаровая поверхность (сфера), при вращении дуги СА этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги AA 1 — шаровой пояс.

Тело, образованное при вращении кругового сектора с углом ϕ ( ϕ ° ) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором .

Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса (рис. 213, а , б ) или из поверхности шарового пояса и боковых поверхностей двух конусов (рис. 213, в, г ).

На рисунке 214 изображены различные элементы шара и сферы (шаровой сектор имеет простейший вид).

Рассмотрим вопрос о вычислении площадей сферы, сегментной поверхности, шарового пояса и шарового сектора.

За площадь сферы, образованной вращением полуокружности вокруг её диаметра, принимают предел, к которому стремится площадь поверхности Ф, образованной вращением вокруг того же диаметра правильной n- звенной ломаной линии, вписанной в полуокружность, при n → + ∞ ( число сторон неограниченно возрастает ).

При вычислении площадей получившихся поверхностей воспользуемся следствиями из теорем 26, 27, 29. Площадь S i ( i = 1, 2, . n ) поверхности, образованной вращением любого звена, равна произведению 2 π , расстояния b i от середины звена до центра сферы и длины m i проекции этого звена на ось вращения, т. е. S i вращ = 2 π • b i • m i .

Так как ломаная — правильная, то все b i равны апофеме a n данной n- звенной ломаной, а m 1 + m 2 + m 3 + . + m n = 2 R и S 1 + S 2 + S 3 + . + S n = 4 π • a n • R . Причём a n = , где p n — периметр данной ломаной. Поскольку ограниченная переменная величина при n → + ∞ становится бесконечно малой, то при n → ∞ апофема a n стремится к радиусу R полуокружности.

Следовательно, предел площади поверхности Ф при n → ∞ равен 4 π R • R = 4 π R 2 . Этот предел и принимается за величину площади сферы радиуса R :

S сферы = 4 π R 2 .

S сегм. поверх = 2 π Rh ,

где h — высота сферического сегмента.

Если же ломаная вписана в дугу ВЕ (см. рис. 215), при вращении которой образуется шаровой пояс, то получим:

S шар. пояса = 2 π Rh ,

где h — высота шарового пояса.

Проделайте эти рассуждения самостоятельно.

в) Площадь поверхности шарового сектора. Эта площадь может быть получена как сумма площадей поверхности сферического сегмента и боковой поверхности одного конуса (см. рис. 213, а, б ) или как сумма площадей поверхности сферического слоя и боковых поверхностей двух конусов (см. рис. 213, в, г ).

Рассмотрим частный случай (см. рис. 213, а, б ). Если R — радиус сферы, h — высота шарового сегмента, то площадь боковой поверхности конуса с вершиной в центре сферы, образующей R , и радиусом основания (докажите это) равна π R , а площадь сегментной поверхности равна 2 π Rh. Значит, для площади шарового сектора справедлива формула

S шар. сект = π R (2 h + ) .

 ЗАДАЧА (3.418). Основанием треугольной пирамиды SABC является равносторонний треугольник АВС , сторона которого равна 4. Известно также, что AS = BS = , a SC = 3. Найти площадь сферы, описанной около этой пирамиды.

Решени е. Решим эту задачу двумя методами.

Первый метод ( геометрич е ски й). Пусть точка О — центр сферы, описанной около данной пирамиды; D — точка пересечения медиан правильного △ АВС ; точка Е — середина отрезка АВ (рис. 216).

Так как точка Е — середина отрезка АВ, то SE ⟂ АВ ( AS = BS ) и СЕ ⟂ АВ ( △ АВС — правильный). Значит, по признаку перпендикулярности прямой и плоскости AB ⟂ ( CSE ) , поэтому ( CSE ) ⟂ ( ABC ) (по признаку перпендикулярности двух плоскостей). Это означает, что прямая OD, а следовательно, и точка О — центр сферы — лежат в плоскости CSE.

В правильном △ AВС имеем: CE = = 2 ; CD = СЕ = . Тогда CL = 2 CD = .

Далее △ BSE ( ∠ BES = 90 ° ): SE 2 = SB 2 – BE 2 = 19 – 4 = 15 (по теореме Пифагора); △ SEC (по теореме косинусов):

cos C = = = ;

△ SLC (по теореме косинусов):

SL 2 = SC 2 + CL 2 – 2 SC • CL • cos C = ⇒ SL = .

В треугольнике CSL имеем = 2 R. Так как в этом треугольнике cos C = , то sin C = = . Тогда R = = : = .

Находим площадь Q сферы:

Q = 4 π R 2 = 4 π • = π .

Второй метод ( коо р динатны й). Введём в пространстве декартову прямоугольную систему координат так, чтобы её начало совпадало с вершиной А данной пирамиды, направление оси абсцисс — с направлением луча АС, ось аппликат была перпендикулярна плоскости основания АВС пирамиды (рис. 217).

В этой системе координат вершины основания пирамиды имеют координаты: А (0; 0; 0), B (2; 2 ; 0), C (4; 0; 0).

Обозначив через х, у, z координаты вершины S пирамиды, найдём их из условий: AS = BS = , CS = 3 .

AS 2 = x 2 + y 2 + z 2 = 19,
ВS 2 = ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19,
C S 2 = ( x – 4) 2 + y 2 + z 2 = 9.

Решая систему уравнений

x 2 + y 2 + z 2 = 19, ( x – 2) 2 + ( y – 2 ) 2 + z 2 = 19, ( x – 4) 2 + y 2 + z 2 = 9,

находим: х = , у = , z = .

Таким образом, вершина S имеет следующие координаты:

S .

Пусть центр O сферы имеет координаты a, b, с, а её радиус равен R. Так как сфера описана около пирамиды SABC, то OA 2 = OB 2 = OC 2 = OS 2 = R 2 . Это соотношение в координатном виде равносильно системе уравнений

a 2 + b 2 + c 2 = R 2 , ( a – 2) 2 + ( b – 2 ) 2 + c 2 = R 2 , + + = R 2 , ( a – 4) 2 + b 2 + c 2 = R 2 .

После вычитания третьего уравнения системы из первого её уравнения получаем:

= 0.

Подставив в это уравнение вместо a и b найденные их значения, получаем с = . Отсюда: R 2 = a 2 + b 2 + c 2 = 4 + + = . Тогда искомая площадь Q сферы равна:

Q = 4 π R 2 = π .

Ответ: π (кв. ед.).

19.8. Объёмы шара и его частей

Рассмотрим фигуру, образованную вращением равнобедренного прямоугольного треугольника с гипотенузой 2 R вокруг прямой, проходящей через вершину прямого угла параллельно гипотенузе (рис. 218, а ). Объём этой фигуры равен разности объёма цилиндра с высотой 2 R , радиусом основания R и удвоенного объёма конуса высоты R , радиуса основания R :

V = π • R 2 • 2 R – 2 • π • R 2 • R = π • R 3 . (*)

Шар радиуса R (рис. 218, б ) и образованную выше фигуру вращения расположим между двумя параллельными плоскостями, расстояние между которыми равно 2 R . Шар при этом будет касаться каждой из данных плоскостей, а фигуру вращения расположим так, чтобы её ось вращения была перпендикулярна этим плоскостям (см. рис. 218). (Плоскость, которая содержит верхнее основание цилиндра и касается сферы в точке N , на рисунке не изображена.)

При х = 0 площади сечений обеих фигур равны π • R 2 ; при х = R площади сечений равны нулю. В остальных случаях площадь сечения шара равна π • ( ) 2 = π • ( R 2 – x 2 ), а площадь сечения другой фигуры (ею является кольцо) равна π • R 2 – π • x 2 . Следовательно, площади равноудалённых от центра шара сечений рассматриваемых фигур равны (относятся, как 1 : 1). Поэтому на основании принципа Кавальери равны и объёмы этих тел. Тогда на основании (*):

V шара = • π • R 3 ,

гдe R — радиус шара.

Для получения объёма шарового сегмента высоты h рассмотрим предыдущую ситуацию для R – h ⩽ x ⩽ R (при h R ) (рис. 218, 219). Применяя принцип Кавальери, получим: объём шарового сегмента равен разности объёма цилиндра высоты h и радиуса основания R и объёма усечённого конуса высоты h и радиусов оснований R и R – h , т. е.

V = π • h • R 2 – π • h • ( R 2 + R • ( R – h ) + ( R – h ) 2 ) =
= π • h 2 • (3 R – h ) .

При h > R объём шарового сегмента можно найти как разность объёма шара и объёма шарового сегмента высоты 2 R – h (рис. 220): V = π • R 3 – • π • (2 R – h ) 2 • (3 R – (2 R – h )) = π • h 2 (3 R – h ) , т. е. получаем ту же самую формулу. Подставляя в эту формулу h = R , получим V = π • R 2 (3 R – R ) = π • R 3 , что соответствует объёму полушара.

Мы показали, что в шаре радиуса R объём любого шарового сегмента высоты h может быть вычислен по формуле:

V шар. сегм = π • h 2 • (3 R – h ) ,

или в другом виде

V шар. сегм = π • h 2 • .

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

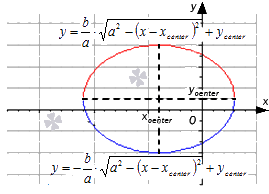
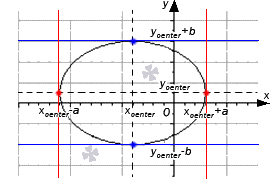
Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

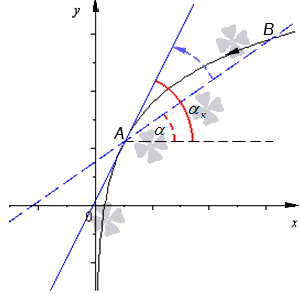
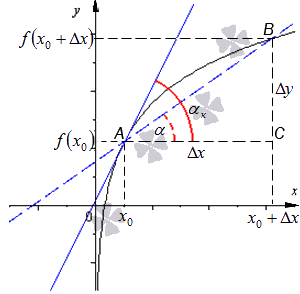
Определения и понятия

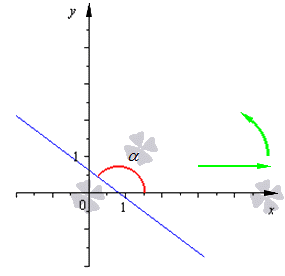
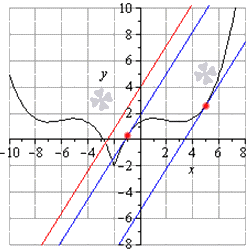
Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
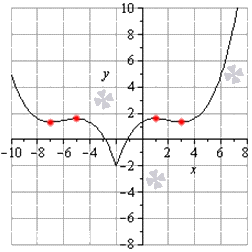
Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

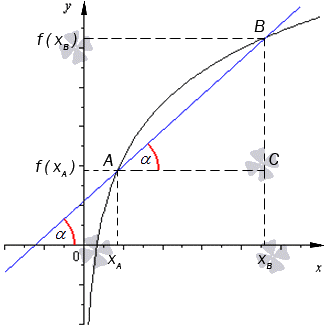
Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

Касательная не существует;
Касательная располагается параллельно о х ;
Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

источники:

http://reader.lecta.rosuchebnik.ru/demo/8285/data/chapter20.xhtml

http://zaochnik.com/spravochnik/matematika/proizvodnye/kasatelnaja-k-grafiku-funktsii-v-tochke/

Источник

Длина окружности на сфере

Сферическая геометрия – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.

По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.

Основные положения сферической геометрии

Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.

Рисунок 1 – Сферическая прямая

Прямые, отрезки, расстояния и углы на сфере

Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла α и радиус сферы R (рис. 2), по формуле длины дуги она равна R α. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. АОС + СОВ = АОВ. Для любой же точки D вне отрезка АВ имеет место сферическое неравенство треугольника : сумма сферических расстояний от D до А и от D до В больше АВ, т.е. AOD + DOB > AOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.

Рисунок 2 – Длина сферического отрезка

Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен π/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.

Рисунок 3 – Сферическая окружность

Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.

Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.

Рисунок 4 – Углы на сфере

Отметим так же, что угол ABC, образованный на сфере двумя дугами большого круга, измеряют углом A`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.

Рисунок 5 – Угол на сфере, образованный дугами большого круга

Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.

Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.

Рисунок 6 – Многогранный угол

Сферический треугольник

Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).

Рисунок 7 – Трехгранный угол

Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.

Рисунок 8 – Описанная окружность сферического треугольника

Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.

Рисунок 9 – Доказательство сферической теоремы о медианах

Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).

Рисунок 10 – Симметричные треугольники

Сумма углов всякого сферического треугольника всегда больше 180°. Разность А + В + С – π = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R 2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.

Если рассматривать двуугольник с углом a, то при 226 = 2π/n (n – целое число) сферу можно разрезать ровно на n копий такого двуугольника, а площадь сферы равна 4πR 2 = 4π при R = 1, поэтому площадь двуугольника равна 4π/n = 2α. Эта формула верна и при α = 2πm/n и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.

Координаты на сфере

Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).

Рисунок 11 – Координаты точки на сфере

В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – θ, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.

Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
3	6

S = 4 π R 2 = π D 2

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x ₀) 2 + ( y — y ₀) 2 + ( z — z ₀) 2 = R 2

Основные свойства сферы и шара

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Касательная, касательная плоскость к сфере и их свойства

Формула. Объём сегмента сферы с высотой h через радиус сферы R:

S = π R(2 h + √ 2 h R — h 2 )

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.