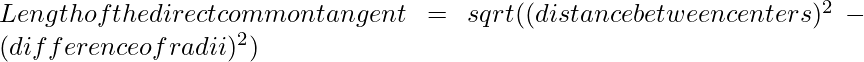Длина общей хорды двух окружностей вычисляется по формуле
Доказательства формул для длин общих касательных и общей хорды двух окружностей
Утверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать.
Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле
что и требовалось доказать.
Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле
Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3,
Простая задача про круги, которая выглядит сложной
Но на деле она точно простая.
Разберём свежую задачу с канала MindYourDecisions. Это не про программирование, но развивает логическое мышление.
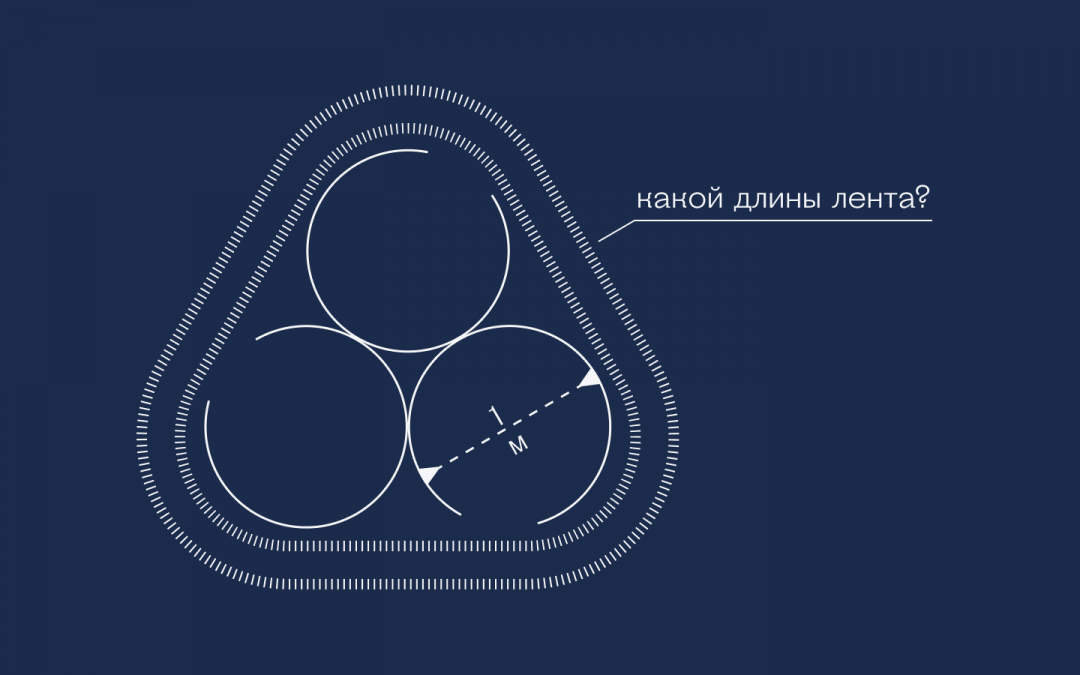
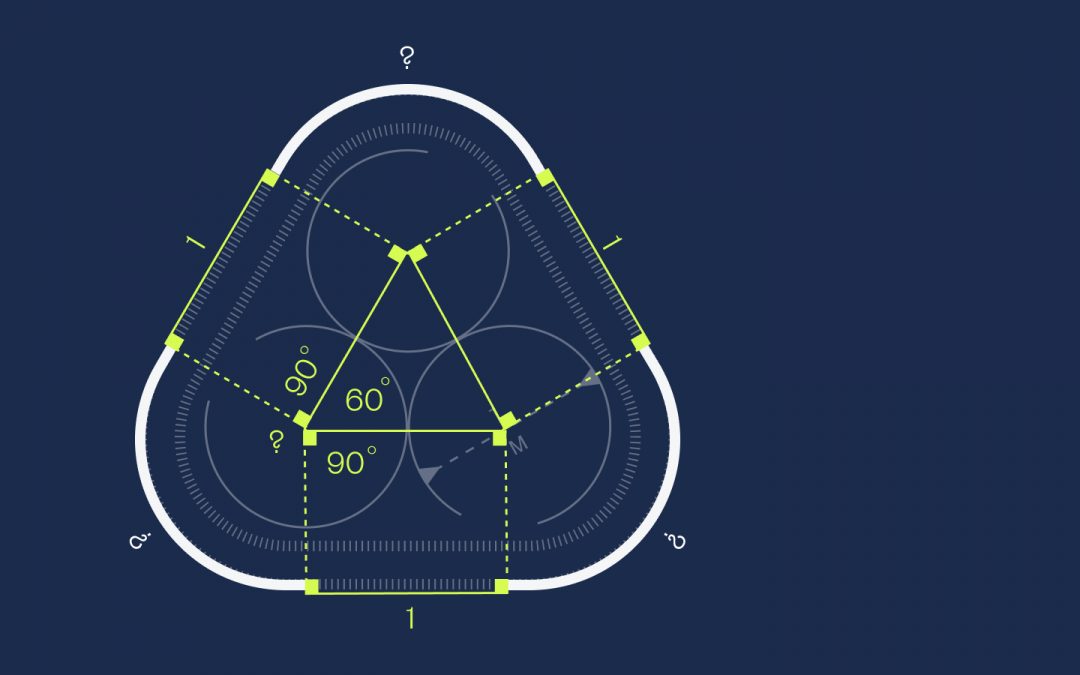
Дано: есть три одинаковых круга с диаметром в 1 метр. Круги соприкасаются друг с другом, а вокруг них натянута эластичная лента.
Что нужно: найти длину этой ленты.
Кажется, что это очень сложная задача, где нужно знать сложные формулы расчёта кривизны и точек натяжения, но на деле всё будет гораздо проще. Если знаете английский — посмотрите оригинальный ролик, там классная анимация:
Строим внутренний треугольник
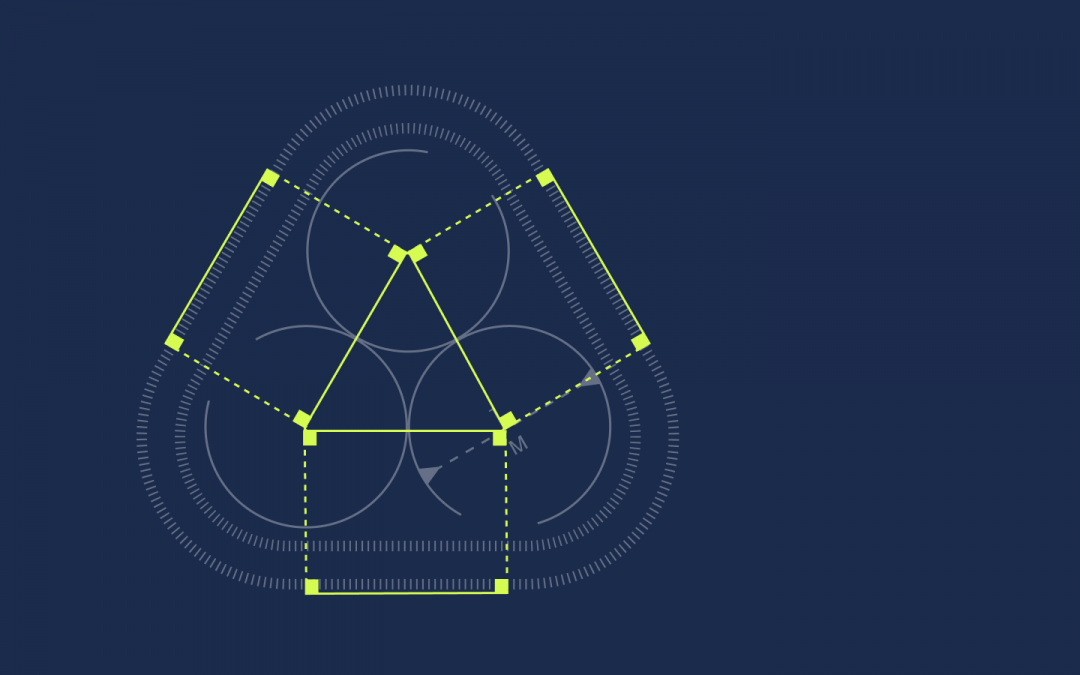
Первое, что мы сделаем, — соединим центры всех кругов в один треугольник:
В геометрии есть такое правило, что если круги касаются друг друга, то через их центры можно провести прямую линию, и точка касания кругов будет лежать на этой линии. Раз у нас диаметр равен 1, то радиус каждого круга равен 0,5. Обозначим это на рисунке:
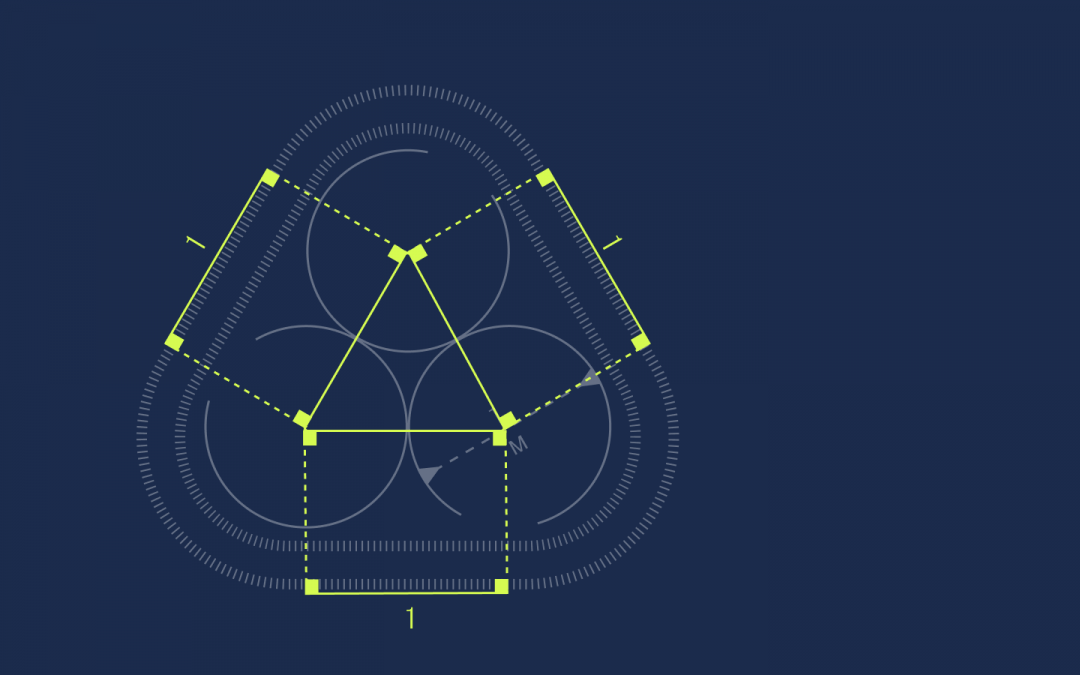
Получается, что длина каждой стороны треугольника равна 0,5 + 0,5 = 1. Запомним это и идём дальше.
Строим проекцию
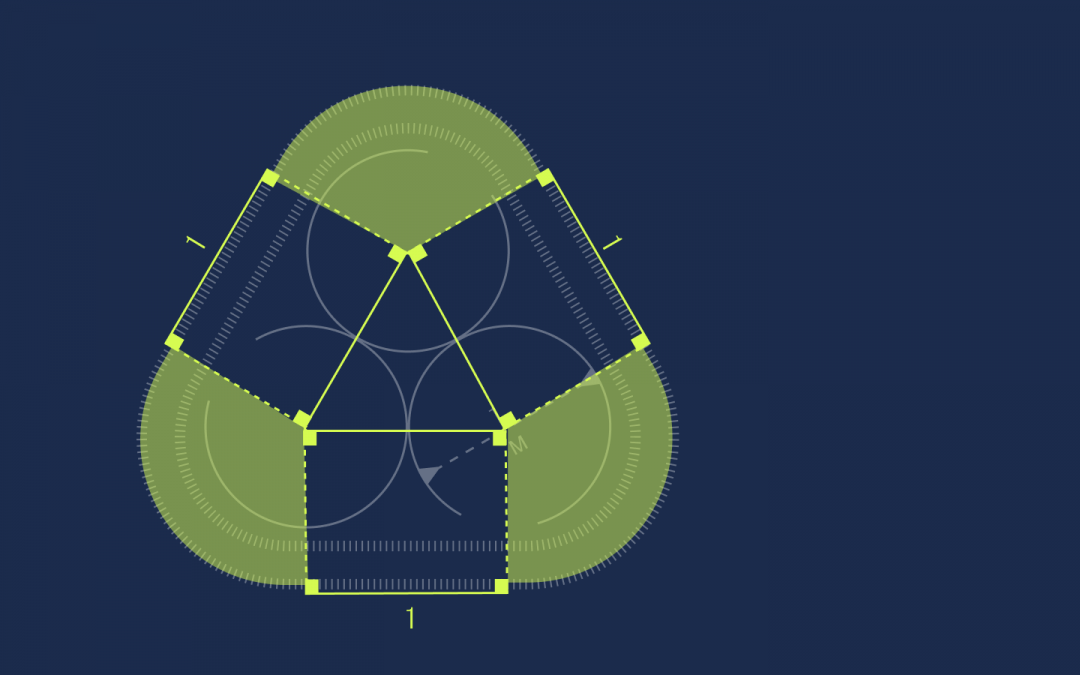
От каждой вершины треугольника проведём под прямым углом линии к ленте:
Получились прямоугольники. У прямоугольников противоположные стороны равны, поэтому раз стороны треугольника равны единице, то и эти отрезки на ленте тоже будут равны единице:
Осталось найти длину оставшихся секций:
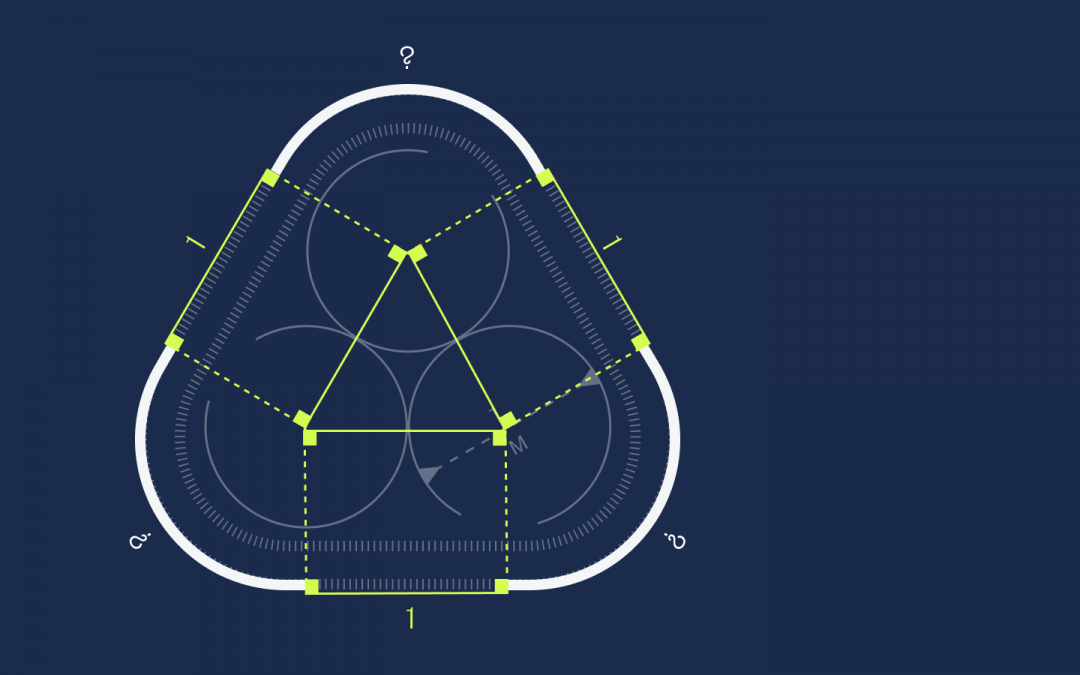
Вычисляем длину секций
Здесь нам поможет знание о том, что полный оборот внутри круга — это 360 градусов.
Так как во внутреннем треугольнике все стороны равны, то это равносторонний треугольник. А раз так, то углы в нём равны 60 градусов. Добавим сюда по два прямых угла по 90 градусов из прямоугольников:
Решаем уравнение: 90 + 60 + 90 + X = 360 → X = 120 градусов.
Но 120 градусов — это ровно треть круга, а у нас таких частей как раз три:
Это значит, что из них можно составить один целый круг. При этом мы знаем, что у этого круга радиус 0,5, а диаметр тогда равен единице. Этого достаточно, чтобы посчитать длину окружности: L = π × d → L = 3,14.
Складываем это число с длинами трёх отрезков и получаем полную длину: 3 + π
Касательная к окружности
О чем эта статья:
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ — ВС = 16 — 12 = 4 (см)
МА 2 = МВ × МС = 16 х 4 = 64
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
(у + R) 2 : 4 = (у + R) × (у — R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°
http://skysmart.ru/articles/mathematic/kasatelnaya-k-okruzhnosti
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given two circles, of given radii, have their centres a given distance apart, such that the circles intersect each other at two points. The task is to find the length of the direct common tangent between the circles.
Examples:
Input: r1 = 4, r2 = 6, d = 3 Output: 2.23607 Input: r1 = 14, r2 = 43, d = 35 Output: 19.5959
Approach:
- Let the radii of the circles be r1 & r2 respectively.
- Let the distance between the centers be d units.
- Draw a line OR parallel to PQ
- angle OPQ = 90 deg
angle O’QP = 90 deg
{ line joining the centre of the circle to the point of contact makes an angle of 90 degrees with the tangent }
- angle OPQ + angle O’QP = 180 deg
OP || QR
- Since opposite sides are parallel and interior angles are 90, therefore OPQR is a rectangle.
- So OP = QR = r1 and PQ = OR = d
- In triangle OO’R
angle ORO’ = 90
By Pythagoras theorem
OR^2 + O’R^2 = (OO’^2)
OR^2 + (r1-r2)^2 = d^2
- so, OR^2= d^2-(r1-r2)^2
OR = √{d^2-(r1-r2)^2}
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void lengtang(double r1, double r2, double d)
{
cout << "The length of the direct"
<<" common tangent is "
<< sqrt(pow(d, 2) - pow((r1 - r2), 2))
<< endl;
}
int main()
{
double r1 = 4, r2 = 6, d = 3;
lengtang(r1, r2, d);
return 0;
}
Java
class GFG
{
static void lengtang(double r1, double r2, double d)
{
System.out.println("The length of the direct"
+ " common tangent is "
+ (Math.sqrt(Math.pow(d, 2) -
Math.pow((r1 - r2), 2))));
}
public static void main(String[] args)
{
double r1 = 4, r2 = 6, d = 3;
lengtang(r1, r2, d);
}
}
Python3
def lengtang(r1, r2, d):
print("The length of the direct common tangent is "
,((d** 2) - ((r1 - r2)** 2))**(1/2));
r1 = 4; r2 = 6; d = 3;
lengtang(r1, r2, d);
C#
using System;
class GFG
{
static void lengtang(double r1, double r2, double d)
{
Console.WriteLine("The length of the direct"
+ " common tangent is "
+ (Math.Sqrt(Math.Pow(d, 2) -
Math.Pow((r1 - r2), 2))));
}
public static void Main(String[] args)
{
double r1 = 4, r2 = 6, d = 3;
lengtang(r1, r2, d);
}
}
PHP
<?php
function lengtang($r1, $r2, $d)
{
echo "The length of the direct common tangent is "
,sqrt(pow($d, 2) - pow(($r1 - $r2), 2)) ;
}
$r1 = 4; $r2 = 6; $d = 3;
lengtang($r1, $r2, $d);
?>
Javascript
<script>
function lengtang(r1 , r2 , d)
{
document.write("The length of the direct"
+ " common tangent is "
+ (Math.sqrt(Math.pow(d, 2) -
Math.pow((r1 - r2), 2))).toFixed(5));
}
var r1 = 4, r2 = 6, d = 3;
lengtang(r1, r2, d);
</script>
Output:
The length of the direct common tangent is 2.23607
Time Complexity: O(logn) because using inbuilt sqrt and pow function
Auxiliary Space: O(1)
Last Updated :
14 Mar, 2023
Like Article
Save Article
Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 23 и 7, а расстояние между центрами окружностей равно 34.
Спрятать решение
Решение.
Пусть центры окружностей — точки O1 и O2, а A и B — точки касания. Проведем через точку B прямую, параллельную O1O2. Точку пересечения этой прямой с O1A обозначим K. Треугольник KAB — прямоугольный.
Возможны два случая расположения окружностей и общей касательной.
Случай 1. Окружности лежат по одну сторону от касательной.
Случай 2. Окружности лежат по разные стороны от касательной.
Обозначим радиусы окружностей R и r, расстояние между центрами окружностей l. В первом случае AK = R − r, во втором случае AK = R + r. Из прямоугольного треугольника KAB находим:
в первом случае
во втором случае
Ответ: 30 или 16.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Рассмотрены все возможные геометрические конфигурации, и получен правильный ответ | 3 |
| Рассмотрена хотя бы одна возможная конфигурация, в которой получено правильное значение искомой величины | 2 |
| Рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неправильное из-за геометрической ошибки | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
06
Сен 2019
Категория: 16 (С5) Планиметр. задачиПланиметрияСправочные материалы
Теорема о длине внешней общей касательной к окружностям
2019-09-06
2019-09-08
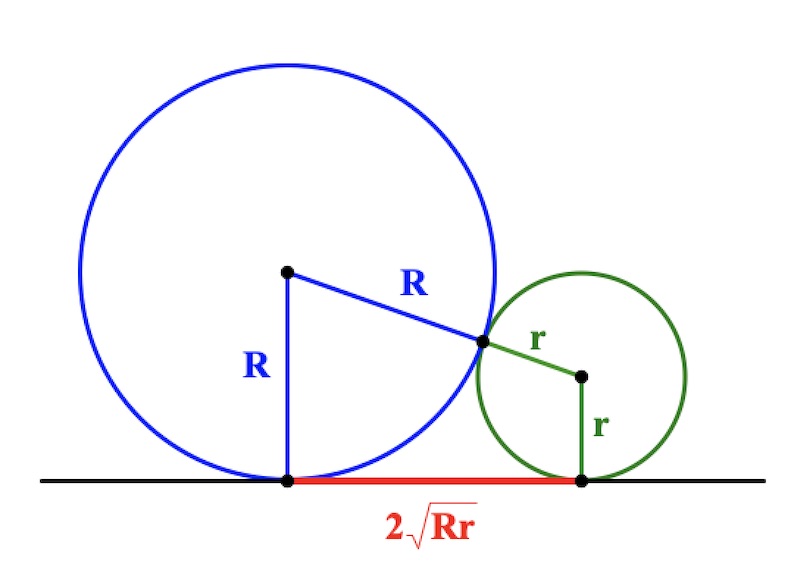
Данное утверждение может быть очень полезно при решении задач на внешне касающиеся окружности.
Теорема Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.
Доказательство смотрите на Youtube канале
Применение теоремы при решении указанной задачи Видео*
О кругах Форда слышали?
Также смотрите применение теоремы при решении задачи
Автор: egeMax |
Нет комментариев
План урока:
Понятие окружности и круга
Касательная к окружности
Взаимное расположение двух окружностей
Понятие окружности и круга
Тарелки, шины, колеса и монеты – все эти предметы имеют одинаковую форму, их называют круглыми. Этот термин понятен каждому, однако в геометрии каждое понятие надо строго определять. Дадим строгое определение понятию окружности:
Та точка, от которой равноудалены все точки, образующие окруж-ть, именуется центром окружности. Обратите внимание, что сам центр частью окружности НЕ считается. Расстояние, отделяющее точки окруж-ти от ее центра, именуют радиусом окружности. Получается, что для построения окруж-ти достаточно знать только ее радиус и центр. Выглядит она так:
Для построения окруж-ти используется специальный инструмент – циркуль. Он представляет собой два длинных стрежня, которые соединены шарниром. На конце одного стержня находится иголка, на конце другого – грифель карандаша или иной пишущий предмет. Сначала необходимо выставить расстояние между концами стержней – оно будет равно радиусу окруж-ти. Потом иголку ставят в центр будущей окруж-ти, после чего поворачивают циркуль так, что его пишущий конец оставил на бумаге след:
Отрезок, соединяющий две точки окруж-ти, именуется хордой. Хорда, проходящая через центр окруж-ти, именуется диаметром окружности.
Особо отметим, что сам диаметр также считается хордой.
Непосредственно из определения окруж-ти вытекает первое важное её свойство – все радиусы, построенные в одной окруж-ти, равны друг другу.
Так как центр окруж-ти делит ее диаметр на два отрезка, каждый из которых – это радиус, то диаметр окружности равен двум ее радиусам:
Традиционно диаметр обозначается буквой D, а радиус – буквой R. Получается, что справедлива формула:
D = 2R
Очевидно, что диаметр длиннее, чем любая другая хорда окружности, не являющаяся диаметром. Докажем это. Пусть хорда AВ не проходит через О, центр окруж-ти (он почти всегда обозначается именно этой буквой). Тогда можно построить ∆AВО:
Мы знаем про неравенство треугольника, согласно которому любая сторона треугольника меньше суммы двух других. В данном случае можно записать, что
AB < OA + OB
ОА и ОВ – радиусы. Обозначив их буквой R, получим, что
AB < R + R
AB < 2R
Величина 2R как раз равна диаметру, то есть
AB < D
ч. т. д.
Ещё раз сформулируем простейшие свойства окруж-ти:
Задание. AВ и СD – диаметры окружности. Верно ли, что BD = АС?
Решение. Выполним построение по условию задачи:
Заметим, что отрезки ОА, ОВ, ОС и ОD одинаковы, ведь они являются радиусами одной окруж-ти:
В итоге получается, что у ∆АОС и ∆ВОD одинаковы две стороны образованный ими угол. Тогда по первому признаку равенства треуг-ков они равны:
Отсюда вытекает, что одинаковы и отрезки АС и BD.
Ответ: верно.
Задание. AВ и CD – диаметры, проходящие через точку О. Длина ВС составляет 13, а АВ – 16. Вычислите периметр ∆АОD.
Решение.
Чтобы вычислить периметр, нужно узнать длины всех сторон треугольника, то есть AD, OD и ОА. Как и в предыдущей задаче, хорды ВС и AD оказываются одинаковыми, так как ∆ОВС и ∆ОАD равны:
AB = DC = 13
Нам известен отрезок AВ, который является диаметром. Поделив его на два, узнаем и радиус:
Задание. Точки А и В на окруж-ти выбраны так, что радиусы АО и ВО пересекаются под углом 40°. Найдите ∠ОВА.
Решение.
Заметим, что в ∆ОAВ есть две одинаковые стороны. Это ОА и ОВ, которые являются радиусами и потому одинаковы. Значит, ∆ОAВ равнобедренный, причем AВ – это его основание. Но тогда углы при основании должны быть одинаковы:
Задание. Угол между радиусом ОА и хордой AВ составляет 60°. AВ имеет длину 29. Каков радиус окруж-ти?
Решение. Исследуем ∆ОAВ. ОВ и ОА являются радиусами одной длины, поэтому он равнобедренный. Тогда ∠ОAВ и ∠ОВА одинаковы:
В итоге получили, что у ∆ОAВ все углы составляют по 60°. Из этого вытекает, что он равносторонний, то есть все его стороны, в частности AВ и ОВ, одинаковы:
OB = AB = 29
Ответ: 29.
Выделяют ещё несколько элементов окруж-ти. Всякие две точки окруж-ти разбивают ее на две кривые линии, которые именуются дугами окружности. Для обозначения дуг используется символ ⋃, после которого пишутся три буквы. Первая и третья буквы указывают на концы дуги, а вторая буква – на какую-либо точку между ними:
Но иногда дугу обозначают только двумя буквами, указывая только ее концы: ⋃AВ. Так поступают, когда ясно, о какой именно из двух дуг идет речь.
Часть плоскости, ограниченная окруж-тью, именуется кругом. То есть окруж-ть – это лишь линия, граница круга, имеющая длину, не имеющая площади. Круг же, наоборот, обладает какой-то площадью, но не имеет длины. На рисунке точка А принадлежит кругу, но НЕ принадлежит окруж-ти:
Очевидно, что любая точка внутри окруж-ти ближе к ее центру, чем точки на самой окруж-ти. Действительно, через центр O и точку A внутри окруж-ти можно построить прямую, которая пересечет окруж-ть в некоторой точке B:
Ясно, что
OB = OA + AB
Значит, отрезок ОВ длиннее ОА. Точки на самой окруж-ти обычно также считают частью круга. Таким образом, круг представляет собой множество точек, удаленных от некоторого центра не более чем на величину заданного радиуса.
Круг можно разделить на две части, либо проведя хорду, либо построив два радиуса. В первом случае образуется фигура, которую называют сегментом. Во втором случае образуется сектор окружности:
Касательная к окружности
Возможно три варианта расположения прямой и окруж-ти относительно друг друга. Если расстояние между центром окруж-тии прямой меньше радиуса, то у них обязательно будут две общие точки. В таком ситуации прямую именуют секущей:
Если же расстояние между прямой и центром окруж-ти больше радиуса, то тогда никаких точек пересечения не будет:
Наконец, возможен особый случай, когда расстояние между прямой и центром окруж-ти в точности равно радиусу. Тогда окруж-ть и прямая будут иметь только одну общую точку. Прямую же в такой ситуации называют касательной к окружности:
Общая точка касательной и окруж-ти именуется точкой касания. Сформулируем одну важную теорему, которая представляет собой основное свойство касательной:
Действительно, предположим, что это утверждение ошибочно, и радиус может образовать с касательной угол, отличный от 90°. Тогда из центра окруж-ти опустим перпендикуляр на прямую, и он упадет на нее в точке B, не совпадающую с точкой касания A. Далее от В на прямой AВ отложим отрезок ВA1, который будет равен AВ.
Получается, что в ∆АОА1 ОВ одновременно высота (ведь ОВ – это перпендикуляр) и медиана (ведь AВ = ВА1). Но это возможно лишь в том случае, если ∆АОА1 – равнобедренный, то есть АО = А1О. Отсюда вытекает, что точка А1 находится на том же расстоянии от О, что и точка А, поэтому она также должна принадлежать окруж-ти. Но тогда прямая имеет уже 2 общие точки с окруж-тью, А и А1, а потому по определению она уже не касательная, ч. т. д.
Оказывается, верна и обратная теорема, которая представляет собой признак касательной.
Действительно, пусть прямая, описанная в теореме, не является касательной. Тогда она имеет не одну, а 2 общие точки с окруж-тью, которые можно обозначить буквами А и А1:
Заметим, что ∆АОА1 равнобедренный, так как две его стороны, ОА и ОА1, представляют собой одинаковые радиусы. Тогда и углы при его основании одинаковы. Если один из них составляет 90°, то и другой также будет составлять 90°. Однако треугольник с двумя прямыми углами не может существовать. Полученное противоречие показывает, что прямая должна быть не секущей, а касательной, ч. т. д.
Из каждой точки плоскости, не принадлежащей кругу, можно провести не одну, а сразу 2 касательных к окруж-ти:
Докажем, что образовавшиеся отрезки AВ и АС (их называют отрезками касательных) одинаковы. Посмотрим на ∆АОС и ∆АОВ. Они прямоугольные, ведь
по свойству касательной. Также у них общая гипотенуза АО и одинаковые катеты ОС и ОВ, которые одинаковы как радиусы одной окруж-ти. Получается, что ∆АOС и ∆АOВ равны, AВ = АС. Также можно запомнить, что и ∠OАС = ∠OAВ, то есть OА оказывается биссектрисой ∠СAВ.
Задание. Угол между двумя касательными к одной окруж-ти составляет 39°.Каков угол между радиусами, построенными к точкам касания?
Решение. Обозначим точки касания буквами С и B, а точку их пересечения буквой А:
Теперь посмотрим на четырехугольник AВОС. Сумма углов в нем, как и во всяком выпуклом четырехугольнике, составляет 360°. По условию известен ∠A, а ∠B и ∠C составляют по 90°. Зная три угла, легко найдем и четвертый:
Задание. Радиус окруж-ти ОМ делит хорду AB пополам. Докажите, что эта хорда будет параллельна касательной к окружности в точке С.
Решение: Обозначим точку касания как С, а середину хорды буквой Н:
Проведем из центра радиусы к точкам А и В. В результате мы получим ∆ОAВ, который оказывается равнобедренным, ведь радиусы ОА и ОВ одинаковы. Так как радиус ОС делит AВ пополам, то он является медианой. Но в равнобедренном треуг-ке медиана, проведенная к основанию, ещё и высота, поэтому прямые ОС и AВ перпендикулярны. В свою очередь касательная также перпендикулярна радиусу. Получается, что хорда и касательная одновременно перпендикулярны третьей прямой, значит, они параллельны, ч. т. д.
Задание. Касательная проходит через точку А окруж-ти. Хорда AВ равна радиусу окруж-ти. Какой угол образуют хорда и касательная?
Решение. Соединим точки А и В с центром окруж-ти:
Хорда по условию имеет такую же длину, как и радиусы, поэтому в ∆ОAВ оказывается три одинаковых стороны. Следовательно, он равносторонний, а у него все углы составляют по 60°. В частности,
∠BAO = 60°
Нам надо найти ∠СAВ. ∠САО должен быть прямым как угол между радиусом и касательной, но ∠САО также является суммой ∠СAВ и ∠ВАО, что позволяет найти ∠СAВ:
Задание. В окруж-ти проведены радиус ОВ длиной 5 и перпендикулярная ему хорда АС, которая отсекает от радиуса отрезок BD длиной 1. Какова длина этой хорды?
Решение:
Сначала можно найти длину OD:
OD = OB — BD = 5 -1 = 4
Теперь исследуем ∆АОD. Он прямоугольный, при этом мы знаем длину его гипотенузы ОА и катет OD. Значит, по теореме Пифагора можно найти и второй катет:
Так как ∆ОАС – равнобедренный, то высота OD– это также и медиана, поэтому DC = AВ = 3. (Примечание: вообще всегда хорда, перпендикулярная диаметру, делится им на одинаковых отрезка). Тогда
AC = DC + AB = 3 + 3 = 6
Ответ: 6.
Задание. Через центр окруж-ти О проходит секущая ОА, а AВ – касательная. Найдите величину радиуса ОВ, если AВ = 12, АО = 13.
Решение. Выполним построение:
Ясно, что угол между отрезками AВ и ОВ должен быть прямым по свойству касательной. Тогда ∆АОВ оказывается прямоугольным, и для него справедлива теорема Пифагора. С ее помощью легко найдем неизвестный нам катет ОВ:
Задание. Длина хорды окружности составляет 72, и находится эта хорда на расстоянии 27 от центра окруж-ти. Каков диаметр этой окруж-ти?
Решение. Ещё раз напомним, что расстояние между точкой и некоторым отрезком – это длина перпендикуляра, опущенного из этой точки на отрезок. С учетом этого построим рисунок:
Здесь отрезок ОН – это как раз перпендикуляр к хорде AВ. Так как ОА и ОВ – радиусы, то ∆ОAВ – равнобедренный, и ОН в нем – это высота, проведенная к основанию. Значит, она является и медианой тоже, то есть делит AВ пополам. Это позволяет найти АН:
AH = AB/2 = 72/2 = 36
∆АОН – прямоугольный, и в нем нам известны оба катета. По теореме Пифагора можно найти и гипотенузу ОА:
Отрезок АО является радиусом. Нам надо в ответе указать диаметр. Диаметр вдвое длиннее радиуса, то есть он равен 45•2 = 90.
Ответ:90.
Задание. Хорда МК образует с касательной КH угол 83°. Найдите угол между этой хордой и радиусом ОМ.
Решение.
Заметим, что ∠ОКН составляет 90°, так как он образован касательной НК и радиусом ОК. Но он состоит из двух углов, ∠МКН и ∠МКО. Так как ∠МКН известен, то можно найти и ∠МКО:
Задание. Точка А находится на расстоянии 8 от центра окруж-ти. Если из точки А провести касательные к окруж-ти, то они образуют угол в 60°. Каков радиус окруж-ти?
Решение:
По условию ∠ВАС = 60°. ОА разбивает этот угол пополам, то есть
∠OAB = ∠OАС = 30°
Посмотрим на ∆AВО. Он прямоугольный, и ∠ОAВ = 30°. Известно, что в прямоугольном треугольнике с углом 30° напротив этого угла находится катет, который вдвое короче гипотенузы. Но гипотенуза в ∆AВО – это ОА, значит, катет ОВ в 2 раза меньше:
OB = OA/2 = 8/2 = 4
ОВ – это и есть искомый нами радиус окруж-ти.
Ответ: 4.
Взаимное расположение двух окружностей
Касаться друг друга могут не только прямая и окруж-ть, но и две окруж-ти. Это значит, что у них есть ровно одна общая точка. Докажем важное утверждение:
Действительно, предположим обратное, что окруж-ти с центрами в точках О1 и О2 касаются в точке К, но точки О1, О2 и К НЕ лежат на одной прямой. Тогда можно построить ∆О1КО2, причем отрезки О1К и О2К будут радиусами соответствующих окруж-тей:
Отложим от точки О1 луч так, чтобы он образовывал с О1О2 угол, равный ∠О2О1K, но не совпадал с лучом ОК. Аналогично отложим луч и от О2 так, чтобы он образовал с О2О1 угол, равный ∠О1О2К. Эти лучи пересекутся в некоторой точке M:
У ∆О1О2К и ∆О1О2М есть общая сторона О1О2, а прилегающие к ней углы одинаковы. По 2-ому признаку равенства треугольников они оказываются равными. То есть
O1K = O1M = R1
O2K = O2M = R2
Выходит, что точка М лежит на том же расстоянии от О1, что и K. Значит, по определению окруж-ти, она принадлежит окруж-ти с центром в О1 и радиусом R1. Аналогично М лежит на том же расстоянии от О2, что и К. Значит, она также принадлежит и второй окруж-ти, с центром в О2. То есть М принадлежит обеим окруж-тям, а значит, является их общей точкой. Но тогда оказывается, что у окруж-тей уже есть сразу две общие точки, М и К, а изначально мы предположили, что они только касаются, то есть имеют 1 общую точку. Противоречие означает, что точки О1, О2 и K обязательно должны лежать на одной прямой, ч. т. д.
Очевидно, что когда три точки лежат на прямой, то каждая из низ либо лежит между двумя другими, либо находится «с краю», то есть по одну сторону от двух других точек. В связи с этим возможны два принципиально различных случая касания окружностей. В первом случае точка касания находится между центрами окруж-тей. Тогда говорят, что окруж-ти касаются внешним образом:
Важно заметить, что при внешнем касании двух окружностей расстояние между их центрами равно сумме их радиусов:
O1O2 = O1K + O2K
Во втором случае одна из окруж-тей находится внутри другой, в таком случае говорят, что окруж-ти касаются внутренним образом. Такое расположение окруж-тей означает, что точка касания находится «с краю»:
При внутреннем касании двух окружностей расстояние между их центрами – это уже разность их радиусов:
O1O2 = O1K — O2K
Заметим, что если в точке касания двух окружностей провести ещё и касательную прямую, то она, во-первых, окажется общей касательной для обоих окруж-тей, а во-вторых, будет перпендикулярна линии, соединяющей их центра:
Однако окруж-ти (не обязательно касающиеся друг друга) могут иметь и другие общие касательные, которые соприкасаются с ними в различных точках. Важно отличать внешние и внутренние касательные. Если обе окруж-ти лежат по одну сторону от касающейся их прямой, то эту прямую именуют внешней касательной. Обычно можно построить сразу две таких внешних касательных:
Однако касательную можно провести и так, что окруж-ти окажутся по разные стороны от нее. В этом случае ее называют уже внутренней касательной:
Задание. Две окруж-ти соприкасаются в точке К. Построена общая касательная к этим окруж-тям, которая касается первой окруж-ти в точке А, а второй – в точке В. Длины хорд АК и ВК равны 15 и 8. Найдите длину отрезка AВ.
Решение:
Решение. Выполним дополнительное построение – проведем общую касательную к окруж-тям через точку К:
Получается, что АМ и КМ – это отрезки касательных, проведенные из одной точки. Мы знаем, что они должны быть одинаковыми:
AM = KM
По той же логике одинаковую длину имеют и отрезки ВМ и КВ, ведь это также касательные к одной окруж-ти, проведенные из одной точки:
BM = KM
В итоге получается, что на рисунке есть два равнобедренных треугольника, ∆АМК и ∆КМВ. Значит, углы при их основании одинаковы. Вместе же они образуют ∆AВК. Попытаемся найти в нем ∠АКВ. Пусть ∠МАК = α, а ∠AВК = β. Тогда можно записать, что
Заметим, что сумма углов в ∆AВК должна составлять 180°, то есть можно записать уравнение:
Задание. Центры окруж-тей, радиусы которых составляют 3 и 10, находятся на расстоянии 25 друг от друга. К ним построена внешняя касательная, касающаяся их в точках А и В. Какова длина отрезка AВ?
Решение. Построим к точкам касания окружностей радиусы, а также проведем через центр меньшей окруж-ти прямую О2Н, параллельную касательной:
Радиусы перпендикулярны касательным. Так как О2Н параллельна AВ, то она также должна быть перпендикулярна радиусам. Получается, что в четырехугольнике AВО2Н все углы прямые, то есть это прямоугольник. Его противоположные стороны одинаковы, поэтому нам достаточно найти длину НО2. Также заметим, что одинаковы и стороны АН и ВО2:
AH = BO2 = 3
Тогда можно найти и длину НО1:
HO1 = AO1 — AH = 10 — 3 = 7
Заметим, что ∆НО1О2 прямоугольный, поэтому длину его катета НО2 можно найти по теореме Пифагора:
Ответ: 24.
Задание. В окруж-ти на радиусе О1А (его длина составляет 10) отмечена точка К на расстоянии 4 от центра окруж-ти О1. Построена ещё одна окруж-ть, которая касается как исходной окруж-ти, так и отрезка О1А в точке К. Какой у неё радиус?
Решение: Соединим центры обоих окруж-тей прямой, которая также пройдет через их точку касания. Также построим радиус О2К:
Обозначим искомый нами радиус буквой R. Теперь посмотрим на отрезок О1О2. С одной стороны, его можно найти как разность радиусов окруж-тей:
Задание на построение. Постройте три окруж-ти, которые касаются друг друга внешним образом. Известны радиусы окруж-тей, они составляют 2, 3 и 4 см.
Решение. Для построения окруж-тей надо лишь знать их центры и величины их радиусов. Радиусы уже известны. Если окруж-ти касаются внешним образом, то расстояние между их центрами равно сумме их радиусов. Значит, в данном случае эти расстояния составят:
2 + 3 = 5 см
2 + 4 = 6 см
3 + 4 = 7 см
Но если расстояния между центрами составляют 5, 6 и 7 см, то это значит, что они образуют треугольник, стороны которого имеют такую же длину. Значит, нам надо просто построить треугольник со сторонами 5, 6 и 7 см, а строить треугольник по известным сторонам мы уже научились в 7 классе:
Сегодня мы узнали многие свойства окруж-ти, а также касательных к ней. Однако это только малая часть геометрических знаний об окруж-ти. В будущих уроках мы узнаем об соотношениях между углами, которые можно в ней провести, вписанных и описанных многоугольниках, вычислениях площадей окруж-ти и способах ее построения.