Площаль прямоугольного треугольника равна половине произведения его катетов — это следует из простого факта, что катеты перпендикулярны друг другу, и запросто можно считать один из них высотой треугольника, а второй — его основанием.
С другой стороны, для угла в 60 градусов соотношение катетов равно 1 к корню из 3: один из катетов ровно в корень из 3 раз больше другого. Конкретно — тот, который лежит напротив этого угла. Итак, имеем, что произведение катетов равно 100 корней из 3, а отношение катетов равно корню из 3. Два уравнения и два неизвестных. В принципе, эта системка решается буквально в уме, и длины катетов оказываются равными 10 и 10 корней из 3.
Как найти стороны прямоугольного треугольника, зная площадь
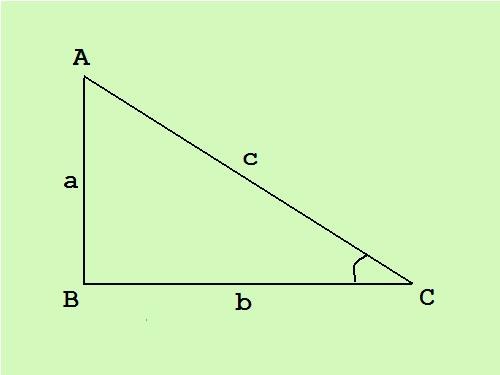
В прямоугольном треугольнике один угол прямой, другие два — острые. Сторона, противостоящая прямому углу, называется гипотенузой, другие две стороны — катеты. Зная площадь прямоугольного треугольника, можно вычислить стороны по известной формуле.
Инструкция
В прямоугольном треугольнике катеты перпендикулярны друг другу, следовательно, общая формула площади треугольника S = (c*h)/2 (где с — основание, а h — высота, проведенная к этому основанию) превращается в половину произведения длин катетов S = (a*b)/2.
Задача 1.
Найдите длины всех сторон прямоугольного треугольника, если известно, что длина одного катета превышает длину другого на 1 см, а площадь треугольника равна 28 см.
Решение.
Запишите основную формулу площади S = (a*b)/2 = 28. Известно, что b = a + 1, подставьте это значение в формулу: 28 = (a*(a+1))/2.
Раскройте скобки, получите квадратное уравнение с одной неизвестной a^2 + a — 56 = 0.
Найдите корни этого уравнения, для чего посчитайте дискриминант D = 1 + 224 = 225. Уравнение имеет два решения: a_1 = (-1 + √225)/2 = (-1 + 15)/2 = 7 и a_2 = (-1 — √225)/2 = (-1 — 15)/2 = -8.
Второй корень не имеет смысла, поскольку длина отрезка не может быть отрицательной величиной, так что a = 7 (см).
Найдите длину второго катета b = a + 1 = 8 (см).
Осталось найти длину третьей стороны. По теореме Пифагора для прямоугольного треугольника c^2 = a^2 + b^2 = 49 + 64, отсюда c = √(49 + 64) = √113 ≈ 10.6 (см).
Задача 2.
Найдите длины всех сторон прямоугольного треугольника, если известно, что его площадь равна 14 см, а угол ACB равен 30°.
Решение.
Запишите основную формулу S = (a*b)/2 = 14.
Теперь выразите длины катетов через произведение гипотенузы и тригонометрических функций по свойству прямоугольного треугольника:
a = c*cos(ACB) = c*cos(30°) = c*(√3/2) ≈ 0.87*c.
b = c*sin(ACB) = c*sin(30°) = c*(1/2) = 0.5*c.
Подставьте полученные значения в формулу площади:
14 = (0.87*0.5*c^2)/2, откуда:
28 ≈ 0.435*c^2 → c = √64.4 ≈ 8 (см).
Вы нашли длину гипотенузы, теперь найдите длины двух других сторон:
a = 0.87*c = 0.87*8 ≈ 7 (см), b = 0.5*c = 0.5*8 = 4 (см).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
В некоторых задачах по геометрии требуется найти площадь прямоугольного треугольника, если известны длины его сторон. Так как длины сторон прямоугольного треугольника связаны теоремой Пифагора, а его площадь равна половине произведения длин катетов, то для решения этой задачи достаточно знать длины двух его любых сторон. Если же нужно решить обратную задачу – найти стороны прямоугольного треугольника по его площади, то потребуется дополнительная информация.
Чтобы найти стороны равнобедренного прямоугольного треугольника по его площади, воспользуйтесь следующими формулами:К = √(2*Пл) или К = √2*√Пл и
Д = 2*√Пл, где
Пл – площадь треугольника,
К – длина катета треугольника,
Д – длина его гипотенузы.Длины сторон при этом будут выражаться в соответствующих площади линейных единицах измерения. Так, например, если площадь задана в квадратных сантиметрах (см²), то длины сторон будут измеряться в сантиметрах (см).Обоснование формул.
Площадь равнобедренного прямоугольного треугольника:
Пл = ½ * К², значит К² = 2 * Пл.
Теорема Пифагора для равнобедренного прямоугольного треугольника:
Д²=2 * К², значит Д = √2 * К.Пусть, например, площадь равнобедренного прямоугольного треугольника равняется 25 см². В этом случае, длина его катетов будет равняться:
К = √2 * √25 = 5√2, а длина гипотенузы:
Д = 2 * √25 = 10.
Чтобы найти длину сторон прямоугольного треугольника по его площади в общем случае, уточните значение какого-либо из дополнительных параметров. Это может быть соотношение катетов или соотношение катета и гипотенузы, один из острых углов треугольника, длина одной из сторон или его периметр.
Для расчета длин сторон треугольника в каждом конкретном случае воспользуйтесь теоремой Пифагора (Д² = К1² + К2²) и следующим равенством:Пл = ½ * К1 * К2, где
К1 и К2 – длины катетов.
Отсюда вытекает, что: К1 = 2Пл / К2 и, наоборот, К2 = 2Пл / К1.
Так, например, если соотношение катетов прямоугольного треугольника (К1/К2) равно Скк,
то К1 = Скк * К2 = Скк * 2Пл / К1, значит,К1 = √(2 * Скк * Пл)
К2 = √(2 * Скк * Пл) / Скк
Д = √((2 * Скк * Пл) + ((2 * Скк * Пл) / Скк))Пусть площадь прямоугольного треугольника – 25 см², а соотношение его катетов (К1/К2) равно 2, тогда по вышеприведенной формуле получается:К1 = √(2*2*25) = 10,
К2 = 10/2 = 5,
Д = √(10²+5²) = √125
Аналогично вычисляются длины сторон и в остальных случаях. Пусть, например, известны площадь (Пл) и периметр (Пе) прямоугольного треугольника.
Так как Пе = К1 + К2 + Д, а Д² = К1² + К2², то получается система из трех уравнений:К1 + К2 + Д = Пе
К1² + К2² = Д²
К1 * К2 = 2Пл,при решении которой в каждом конкретном случае определяются длины сторон треугольника.
Пусть, например, площадь прямоугольного треугольника 6, а периметр – 12 (соответствующих единиц).
В этом случае получается следующая система:К1+К2+Д = 12
К1² + К² = Д²
К1 * К2 = 12,
решив которую, можно узнать, что длины сторон треугольника равны 3, 4, 5.
2
1 ответ:
0
0
Площадь прямоугольного треугольника равна половине произведения его катетов. Поэтому ab=2S(a и b — катеты(пусть b — катет с прилежащим к нему углом 30 градусов)). Воспользуемся тангенсом угла 60 градусов.. Подставляем вместо b это выражение в формулу ab=2S
. Теперь находим b
. Подставляй вместо S значение и получишь ответ:)
Читайте также
рассматриваем каждый раз два прямоугольных треугольника, где катеты равны, а значит равны и гипотенузы. Катеты равны, так как один общий, а второй АО=ОВ. Гипотенуза — расстояние от точки на перпендикуляре до точки А или В.
№ 7. S=Sквадрата — Sпрямоугольника
Sквадрата = 7*7=49; Sпрямоугольника=4*3=12, отсюда, S=49-12=37
№ 8.
SΔ=Высота * Основание : 2 = 80*57:2=2280
Если ты имеешь ввиду , треугольник со сторонами 1 см , 2 см , 3 см то нет , не существует
<span>решение в картинке, ответ: 7,5 </span>
Биссектриса-это луч с началом в вершине угла, делящий угол на два равных угла.
Учитель по математике, просто заглянула вперёд и немного нам рассказала.
