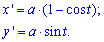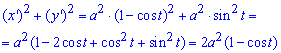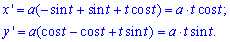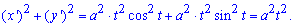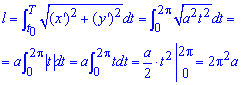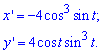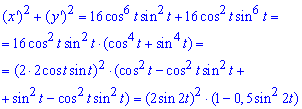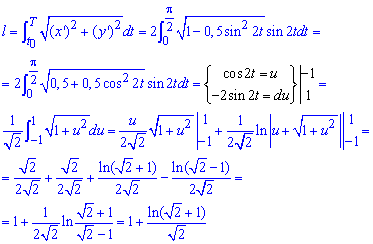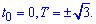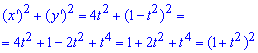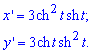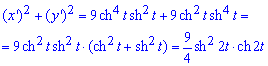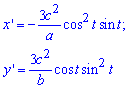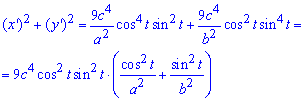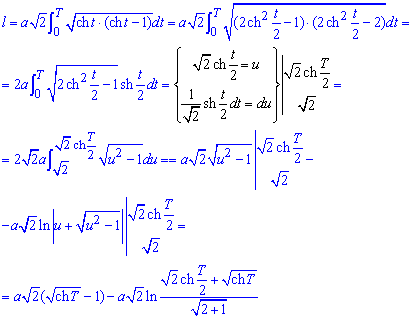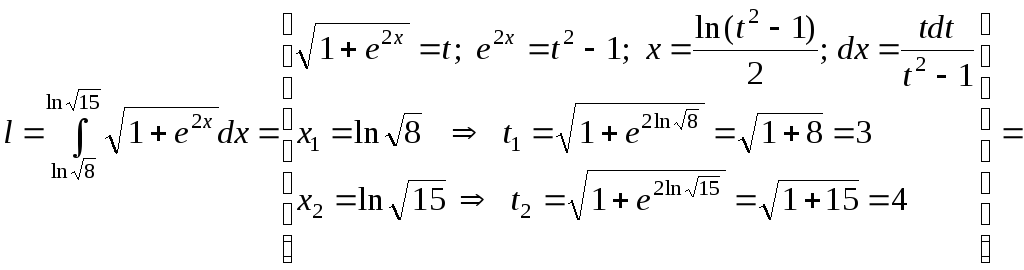При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда
,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
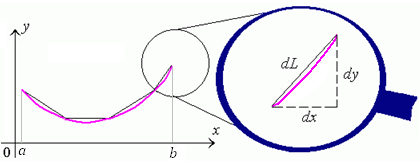
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
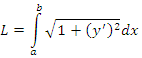 . . |
Пример 5.
Если кривая C задана уравнениями x=x(t), y=y(t) (t[t0;T]), где x(t) и y(t) непрерывные на [t0;T] функции, то длина дуги кривой С равняется определенному интегралу
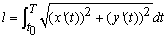
Примеры подобрано из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления дуги кривой, заданной в параметрической форме будут повторяться из примера в пример.
Часть заданий обязательно проиллюстрируем графиками кривых.
Как найти длину дуги, заданной в параметрическом виде?
Пример 2.127-2443 Найти длину дуги кривой, заданной в параметрическом виде
x=a(t-sin(t)), y=a(1-cos (t)), tє[0;2pi].
(См. 2.100)
Вычисление: Найдем производные по переменной t функций:
Пределы интегрирования берем из условия: [0;2pi].
Выражаем подинтегральную функцию:
Интегрированием находим длину дуги кривой на заданном отрезке:
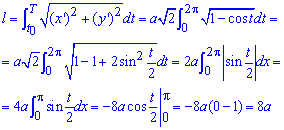
Для выведения формулы использовали известные тригонометрические формулы.
Длина дуги равна 8a единиц.
Пример 2.128 (2444) Найти длину дуги кривой, заданной параметрически
x=a(cos(t)+t*sin(t)), y=a(sin(t)-t*cos(t)), tє[0;2*Pi]. (См. 2.103)
Вычисление: Вычисляем производную по переменной t от параметрических уравнений координат функции:
Пределы интегрирования записываем из начального условия: [0;2*Pi].
Складываем подинтегральную функцию:
Ее вид чрезвычайно прост, а длина дуги параметрической кривой через интеграл вычисляется быстро:
Пример 2.129 (2442) Найти длину дуги кривой, заданной параметрически
x=cos4(t), y=sin4(t).
Вычисление: Найдем производные по переменной t от параметрически заданных координат:
Имеем пределы интегрирования:
[0;Pi/2], поскольку функция принимает только положительные значения.
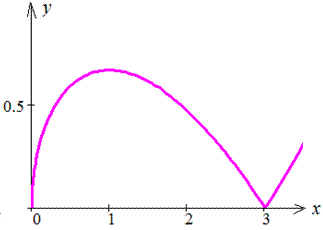
График кривой приведен на рисунку
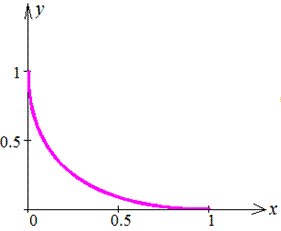
Складываем уравнение подинтегральной функции:
Однократно применив замену переменных и метод интегрирования частями находим длину дуги кривой:
Интеграл достаточно распространен для такого сорта примеров, поэтому вспомните все формулы интегрирования, которые в результате дают логарифм.
Пример 2.130 Найти длину дуги кривой, заданной параметрически
x=t2,y=t-t3,
Вычисление: Первым делом находим производные параметрически заданных координат по переменной t:
x’=2t; y’=1-t2.
Крайние точки известны: 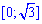
из условия y=0 определяем
Функция симметрична относительно оси Ox, поэтому принимаем 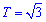
График кривой на положительной части оси абсцисс изображен ниже
Составим уравнение подинтегральной функции:
Последним шагом находим длину дуги кривой на заданном отрезке:
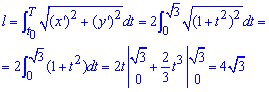
Интеграл достаточно быстро вычисляется.
Пример 2.131 (2445.1) Найти длину дуги кривой, заданной в параметрическом виде
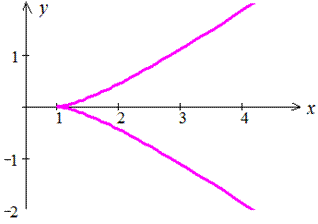
x=ch3(t), y=sh3(t), [0;T]
Вычисление: Найдем производные от гиперболичного косинуса и синуса по t:
Пределы интегрирования известны: [0;T].
График кривой приведен на рисунке
Вычислим подинтегральную функцию:
Учитывая формулы для гиперболичных функций при вычислении интеграла синус гиперболический от двойного угла вносим под дифференциал.
В результате придем к формуле, которую и без замены переменных можем проинтегрировать.
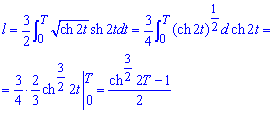
Пример 2441 Найти длину дуги эволюты эллипса, заданной параметрически 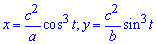
Вычисление: Найдем производные параметрически заданных координат эволюты эллипса:
Пределы интегрирования: [0;Pi/2] (оси координат являются осями симметрии).
График эволюты эллипса имеет вид
Складываем уравнение подинтегральной функции:
Чтобы найти длину дуги эволюты эллипса придется превратить подинтегральную функцию, потом свести ее под известные интегралы.
Чтобы облегчить чтение формул на середине вычислений выполняем замену переменных и, соответственно, пересчет пределов интегрирования.
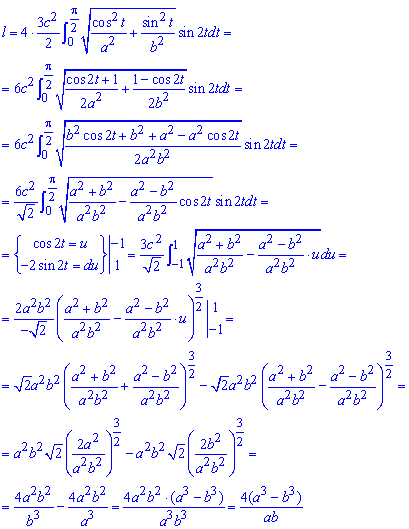
Также последние строки показывают, что умение работать с дробями Вам тоже пригодятся.
Если не упрощать, то получим тяжелую для чтения формулу с иррациональными слагаемыми.
Пример 2445 Найти длину дуги кривой, заданной параметрически
x=a(sh(t)-t), x=a(ch(t)-1, tє[0;T].
Вычисление: Вычислим производные от параметрических координат кривой:
x’=a(ch(t)-1;
y’=a*sh(t).
Пределы интегрирования заданы: [0;T].
Подносим к квадрату производные параметрических координат линии:
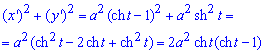
За формулой находим длину дуги кривой:
для этого превращаем подынтегральную функцию, а дальше методом замены переменных вычисляем интеграл:
Конечная формула длины дуги кривой содержит зависимости от косинуса гиперболического.
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:
В более общем случае, если у нас задана функция
в декартовых координатах и стоит задача найти длину дуги этой кривой между точками
и
,
нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение
означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.
Вычисление длины дуги кривой
Если
функция
и ее производная
непрерывны на отрезке
,
то длина дуги кривой на отрезке
определяется по формуле:
.
Пример 45.
Вычислить
длину дуги кривой
от
до
.
Решение.
Найдем
производную заданной функции:
.
Подставим производную в формулу для
вычисления дуги кривой. Границы промежутка
интегрирования равны:;
.
(ед.).
3.2.6. Вопросы для самоконтроля
-
Что
называется интегральной суммой? -
Что
называется определенным интегралом
функции на отрезке? -
Каков
геометрический смысл определенного
интеграла? -
Перечислите
основные свойства определенного
интеграла. -
Запишите
формулу Ньютона-Лейбница. -
В
чем заключается интегрирование методом
подстановки определенного интеграла? -
В
чем заключается метод интегрирования
по частям определенного интеграла? -
Запишите
формулу интегрирования по частям. -
Что
называется несобственными интегралами? -
Какие
бывают виды несобственных интегралов? -
Какие
существуют геометрические приложения
определенного интеграла? -
Как
вычислить площадь плоской фигуры,
ограниченной заданными линиями? -
Как
вычислить объем тела вращения фигуры,
ограниченной линиями, вокруг координатной
оси? -
Как
вычислить длину дуги плоской кривой?
Литература
Основная:
-
Вища
математика: Навчальний посібник: У 2
ч./ Ф.М. Ліман, В.Ф. Власенко, С.В. Петренко
та інші, За заг. ред. Ф.М. Лимана. – Суми;
ВТД „Університетська книга”, 2006. –
614 с. -
Кудрявцев
В.А., Демидович Б.П. Краткий курс высшей
математики. – 6-е изд. – М.: Наука, 1986. –
576 с. -
Шипачев
В.С. Высшая математика: Учебник для
ВУЗов – 6-е изд. – М.: Высш. шк., 2003. – 479
с. -
Высшая
математика для экономистов: Учебник
для ВУЗов / Н.Ш. Кремер, Б.А. Путко, И.М.
Тришин, М.Н. Фридман; Под ред. проф. Н.Ш.
Кремера. – 2-е изд. – М., ЮНИТИ, 2002. – 471
с. -
Минорский
В.П. Сборник задач по высшей математике.
– 10-е изд. – М.: Наука, 1969. – 352 с. -
Шипачёв
В.С. Задачник по высшей математике:
Учебн. пособие для ВУЗов – 3-е изд. –
М.: Высш. шк., 2002. – 304 с.
Дополнительная:
-
Пискунов
Н.С. Дифференциальное и интегральное
исчисления для втузов. Т. 1, 2. – 7-е изд.
– М.: Наука, 1966. – т.1 – 552 с., т.2 – 312 с. -
Бермант
А.Ф., Араманович И.Г. Краткий курс
математического анализа для втузов.
– 7-е изд. – М.: Наука, 1971. – 736 с. -
Шипачёв
В.С. Основы высшей математики: Учебн.
пособие для ВУЗов – 5-е изд. – М.: Высш.
шк., 2003. – 479 с. -
Соболь
Б.В., Мишняков Н.Т., Поркшеян В.М.
Практикум по высшей математике. –
Ростов н/Д: Изд-во «Феникс», 2004. – 640
с.
Индивидуальные задания для расчетно-графической работы
ЗАДАНИЕ
1. Вычислить пределы.
1.
а)
;
б);
в);
г)
; д)
.
2.
а)
;
б);
в);
г)
;
д).
3.
а)
;
б);
в);
г)
;
д).
4.
а)
;
б);
в);
г)
;
д).
5.
а)
; б)
;
в);
г)
;
д).
6.
а)
;
б);
в);
г)
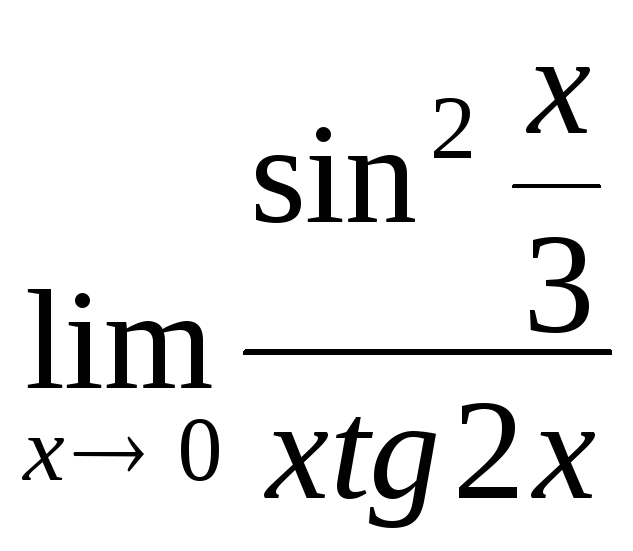
.
7.
а)
;
б);
в);
г)
;
д).
8.
а)
;
б);
в);
г)
;
д).
9.
а)
;
б);
в);
г)
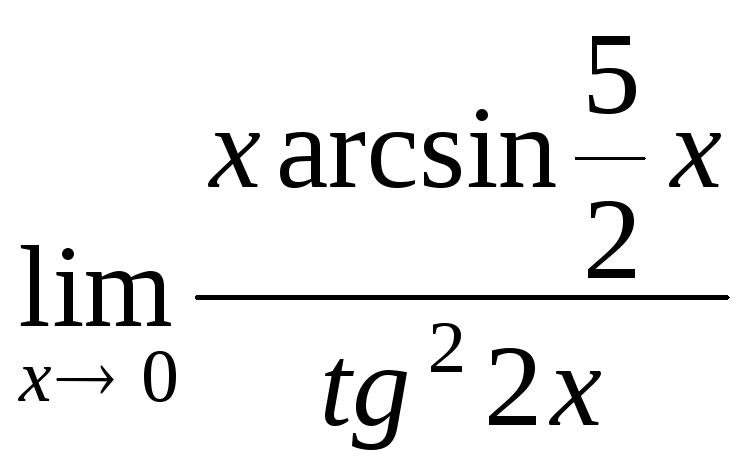
д).
10.
а)
;
б);
в);
г)
;
д).
11.
а)
;
б);
в);
г)
;
д).
12.
а)
;
б);
в);
г)
;
д).
13.
а)
;
б);
в);
г)
;
д).
14.
а)
;
б);
в);
г);
д).
15.
а)
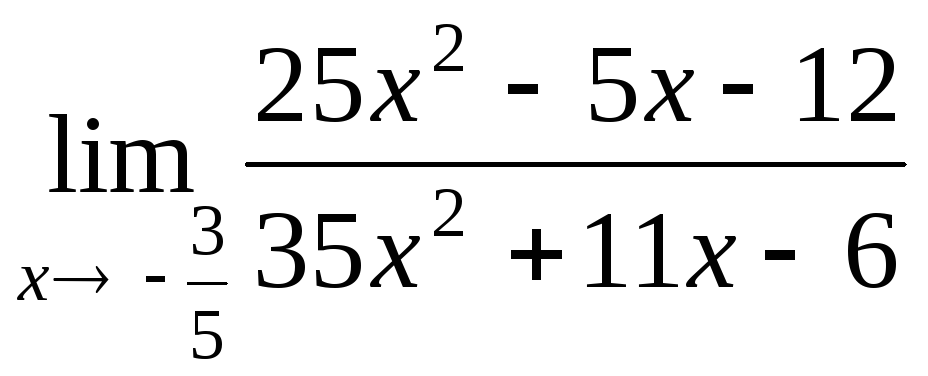
б);
в);
г)
;
д).
16.
а)
;
б);
в);
г);
д).
17.
а)
;
б);
в);
г); д)
.
18.
а)
;
б);
в);
г)
;
д).
19.
а)
;
б);
в);
г)
;
д).
20.
а)
;
б);
в);
г)
;
д).
21.
а)
;
б);
в);
г)
;
д).
22.
а)
;
б);
в);
г)
;
д).
23.
а)
;
б);
в);
г);
д).
24.
а)
;
б);
в);
г);
д).
25.
а)
;
б);
в);
г);
д).
26.
а)
;
б);
в);
г);
д).
27.
а);
б);
в);
г)
;
д).
28.
а)
;
б);
в);
г)
;
д).
29.
а)
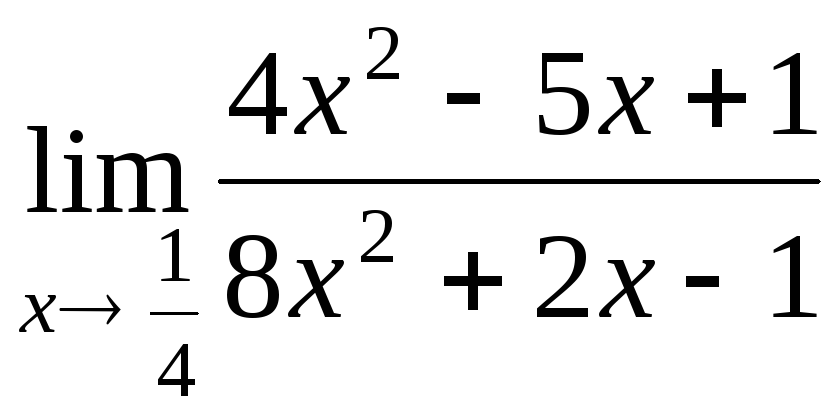
б);
в);
г)
;
д).
30.
а)
;
б);
в);
г)
; д)
.
ЗАДАНИЕ
2. Найти производные данных функций,
используя формулы дифференцирования
в произвольной точке.
1.
а)
б)у
= ln arctg x2; в)
;
г)
; д)
; е)х2
+ cos xу2
– 2у
= 0.
2.
а)
б)у
= 5ln ctg 2; в)
;
г)
; д)
;
е) sinx
– arctg y
+ ху
= 0.
3.
а)
; б)
у
= ln arctg2
x2; в)
;
г)
; д)
; е)
ех
– cosху
– y3
= 0.
4.
а)
б)у
= arctg3; в)
г)
д)
; е)х
sin у
– у cos x
– 2 = 0.
5.
а); б)
; в)
;
г); д)
; е)
ex
– x2
+ yex
– e y
= 0.
6.
а)
б)у
= ln4
cos; в)
;
г)
д)
; е)
2x –
sin 2x
– х2y2
= 0.
7.
а)
; б)
;
в);
г)
; д)
; е)
exy
– x2
+ y2
= 0.
8.
а)
б)у
= sin3
еtg 3x; в)
;
г)
; д)
; е)y
sin x
+ cos y
= 0.
9.
а)
; б)
; в)
;
г)
; д)
; е)
cos (x
– y)
– 2x
+ 4y
= 0.
10.
а)
; б)у
=
; в)
;
г)
; д)
; е)
.
11.
а)
; б)у
=
; в)
;
г); д)
; е)xy
+ ln y
+ cos 2x =
0.
12.
а)
; б)у
= ln arcsin x2; в)
;
г)
; д)
; е)
.
13.
а)
; б)у
= arccos; в)
;
г)
; д)
; е)
(x
+ y)2
= x
– y.
14.
а)
; б)у
= log5sin(x2
+
2x
+
2); в);
г)
; д)
; е)y
ln x
– x
ln y
= x
+ y.
15.
а)
;
б); в)
;
г)
; д)
; е)x3
y3
– 2 x y
+ 3 = 0.
16.
а)
; б)у
= tg3arcsin;
в);
г)
; д)
; е)x2
y2
– cos (x
+ у2)
= 0.
17.
а)
; б)у
= arctg3;
в);
г)
; д)
; е)
cos (x y)
– 2x
+ 3у2
= 0.
18.
а)
; б)
;
в);
г)
; д)
; е)
.
19.
а)
; б)
; в)
;
г); д)
; е)
5x2
y2
– 7y
+ 9 = 0.
20.
а)
; б)у
= arctg3(x5
– 3x); в)
;
г)
; д)
; е)x3
y3
– 2 x y
– 3 = 0.
21.
а)
; б)у
= ln tg2;
в)
;
г)
; д)
; е)x2
+ x4
y2
+ у4
= 3.
22.
а);
б)у
= ln();
в);
г); д)
; е)x2
+ sin y2
– x
y = 0.
23.
а)
;
б);
в);
г); д)
; е)x3
+ y3
– 3 x2
y = 0.
24.
а)
; б)у
= sin; в)
;
г)
д)
; е)x4
+ y4
– x2
y2
= 0.
25.
а)
; б)у
= log3arcsin3x;
в);
г)
; д)
; е)y
– x
еу
– sin ху
+ 3 = 0.
26.
а)
; б)у
= ln2arcsin; в)
;
г)д)
; е)y3
+ еху
+ x3
– 4 = 0.
27.
а)
; б)у
=
;
в);
г)
; д)
; е)x y
+ 2еу
– 4 = 0.
28.
а)
; б)у
=
;
в);
г)
; д)
; е)x3
y3
– sin y
+ 3 = 0.
29.
а)
; б)у
= arcsin;
в);
г)
; д)
;
е) 2sinx
+
cos xy
2
= 0.
30.
а)
; б)у
= tg sin2cos4x; в);
г)
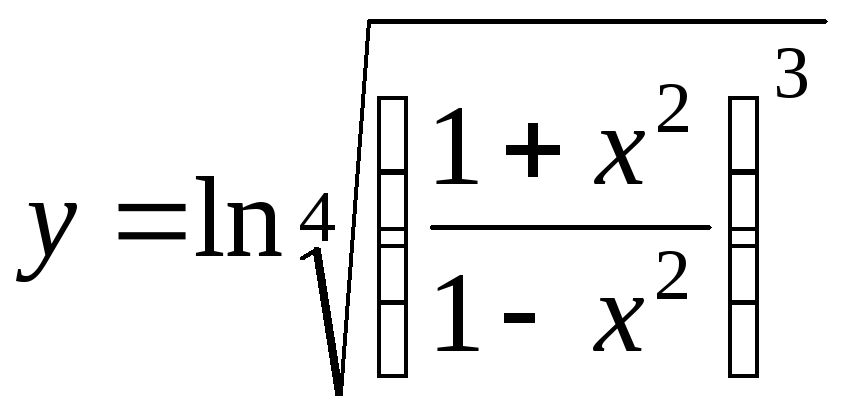
; е)x3
y2
– cos y
+ 4 = 0.
ЗАДАНИЕ 3. Провести
полное исследование функций по схеме:
-
Область
определения функции. -
Непрерывность
функции, вертикальные асимптоты. -
Точки
пересечения функции с осями координат. -
Четность,
нечетность. -
Периодичность.
-
Промежутки
возрастания, убывания, экстремумы
функции. -
Промежутки
выпуклости, вогнутости, точки перегиба. -
Наклонные
асимптоты. -
Построение
графика.
1.
а) y
=
;2.
а) y
=
;
б)
у
= х;
б) y
= x
lnx;
3.
а) y
=
;4.
а) y
=
б)
y
= x
– lnx;
б) y
=
;
5.
а) y
=
;6.
а) y
=
;
б)
y
= exe–x;
б) y =
xe–x;
7.
а) y
=
;8.
а) y
=
;
б)
y
=
;
б) y
=
;
9.
а) у
=
;10.
а) у
=
;
б)
у =
;
б)у
=
;
11.
а) у
=
;12.
а) у
=
;
б)
у
=
;
б)у
=
;
13.
а) у
=
;14.
а) у
=
;
б)
у
=
;
б)у
=
;
15.
а) у
=
;16.
а) у
= х
+
;
б)
у
=
;
б)у
=
;
17.
а) у
=
;18.
а) у
=
;
б)
у
= ln(x2
+ 4x);
б) y
=
;
19.
а) у
=
;20.
а) у
=
;
б)
у
=;
б)у
= х2е–х;
21.
а) у
=
;22.
а) у
=
;
б)
у
= х
– 2lnx;
б) у
=
;
23.
а) у
=
;24.
а) у
=
;
б)
у
=
;
б)у
=
;
25.
а) у
=
;26.
а) у
=
;
б)
у
=
;
б)у
=
;
27.
а) у
=
;28.
а) у
=
;
б)
у
= х2
lnx;
б) у
=
;
29.
а) у
=
;30.
а) у
=
;
б)
у
=
;
б)у
=
.
ЗАДАНИЕ
4. Вычислить неопределенные интегралы.
1. 1); 2)
; 3)
;
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как вычислить длину дуги кривой?
Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий
Каршинский филиал
Аннотация: Такое впечатление, что сборник Кузнецова — очень популярный поставщик задач по приложениям определённого интеграла в контрольные работы. И в разделе IV-Интегралы вы можете найти порядка сотни прорешанных примеров по теме (Задачи 17-19). Решение: аналитические условия задают левую верхнюю дугу астроиды. Причём параметрические уравнения «прорисовывают» эту кривую справа налево, но, как я только что отметил, сейчас нас это не волнует, и асфальтный каток едет дальше. Пусть
некоторая функция непрерывна на отрезке и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой : Другой хорошей новостью является тот факт, что в практических примерах, как правило, не нужно строить чертежа. Это была единственная иллюстрация в статье, чтобы вы быстрее поняли, о чём вообще идёт речь.
Ключевые слова: Другой хорошей новостью является тот факт, что в практических примерах, как правило, не нужно строить чертежа, как вычислить длину дуги кривой.
How to calculate the arc length of a curve?
Mahsud Tulgin oglu Usmonov maqsudu32@gmail.com Tashkent University of Information Technologies
Karshi branch
Abstract: It seems that Kuznetsov’s collection is a very popular supplier of tasks for applications of a certain integral to control papers. And in section IV-Integrals you can find about a hundred solved examples on the topic (Problems 17-19). Solution: analytical conditions set the upper left arc of the astroid. Moreover, the parametric equations «draw» this curve from right to left, but, as I just noted, now we do not care about this, and the asphalt roller goes on. Let some function be continuous on a segment, and its graph on this interval is a curve or, equivalently, an arc of a curve: Another good news is the fact that in practical examples, as a rule, you
do not need to build a drawing. This was the only illustration in the article, so that you quickly understand what it is all about.
Keywords: Another good news is the fact that in practical examples, as a rule, you do not need to build a drawing, how to calculate the arc length of a curve.
Помимо нахождения площади и объёма тела вращения, вездесущий определённый интеграл позволяет рассчитать и другие показатели, в частности длину дуги кривой.
И в данной статье мы узнаем, как вычислить данную величину, если линия
задана функцией у ~ , либо параметрически ~ или же уравнением
r ~ в полярной системе координат. Для каждого случая будут разобраны практические примеры с подробными комментариями о типичных особенностях решения этой задачи. Более того, по ходу изложения материала вас ждёт специальное предложение, которое должно понравиться 
Пусть некоторая функция непрерывна на отрезке l-13, и её график на данном промежутке представляет собой кривую или, что то же самое, дугу кривой АВ ;
Y
В предположении о непрерывности производной ^ ^ на ^ длина
кривой АВ выражается формулой:
г __ь
12 или компактнее: й
Согласно геометрическому смыслу, длина не может быть отрицательной, и это заведомо гарантируется неотрицательностью подынтегральной функции
|| II
(при разумеющемся условии а <ъ ). Таким образом, в данной задаче не возникает дополнительных хлопот по поводу того, как и где «петляет» график (выше оси, ниже оси и т.д.).
Другой хорошей новостью является тот факт, что в практических примерах, как правило, не нужно строить чертежа. Это была единственная иллюстрация в статье, чтобы вы быстрее поняли, о чём вообще идёт речь. Впрочем, начнём с кривой, которую всем вбили в голову ещё в далёком детстве
=)
Пример 1
Вычислить длину дуги параболы у~х от точки ^ до точки Решение: принимая во внимание «иксовые» координаты точек, определяем
пределы интегрирования а ~ ^ ^ ~~ 2
и используем формулу:
А вот и первый камень преткновения. Интеграл данного вида детально разобран в Примере № 5 урока Сложные интегралы, он интегрируется по частям и сводится к себе. Сначала удобно найти первообразную:
Интегрируем по частям:
Таким образом:
Открываем одиночной «звёздочкой» основное решение и используем формулу Ньютона-Лейбница:
S Г4+-Л7
Vr7 — —— + —In
2 + S
sd. « 3,17 ed.
Ответ:
Скрупулёзно не проверял, но если взглянуть на параболу, то очень и очень похоже на правду. Громоздких и страшных результатов бояться не нужно, равно, как и длинных решений!
Следующие разминочные задачи для самостоятельного решения Пример 2
Вычислить длину дуги полукубической параболы
до точки
Интеграл здесь будет значительно проще, чем в предыдущем примере. Однако за кажущейся простотой нередко скрывается коварство. Так, вроде бы
похожее условие «Вычислить длину дуги полукубической параболы ? = ^ на
отточки
промежутке 1 ‘ А» далеко не эквивалентно и приводит к совершенно другому ответу.
Да, в рассматриваемом типе задач обычно не требуется выполнять чертёж, но всегда полезно, а иногда и очень важно знать, что это за линия и КАК выглядит её график 
Пример 3
Вычислить длину дуги кривой х ~111С0Е у, 3
Это более распространённый вариант формулировки — когда промежуток интегрирования указан в виде двойного неравенства.
А что тут смущает? Люди без комплексов давно интегрируют по любой переменной, и я ещё в статье Объем тела вращения предлагал вам расширить свои взгляды.
Обратная функция и её производная непрерывны на отрезке
1 = 1+(*;<>))>
поэтому применима зеркальная формула а .
естественно, уже «игрековые» пределы интегрирования.
где а и ^
Кстати, в первом примере можно рассмотреть правую ветвь параболы
‘= Лу 1 < у <4
^ с пределами интегрирования ~ — ~
правда, хрен редьки не слаще. Хотя любители оценят, интеграл получается трудный, но вполне реалистичный.
В следующем параграфе рассмотрим критически важную вещь, касающуюся всех задач урока:
Как найти длину дуги кривой, если линия задана параметрически?
Если линия задана параметрическими уравнениями х ~ у ~ , то при выполнении некоторых условий, на которых я не буду останавливаться, длина
АВ
дуги кривои
L <1 <1
которая прочерчивается при изменении параметра в пределах 1 ~1″1, рассчитывается по формуле:
где ^ — значения, определяющие точки А и ^. В начале урока о площади и объёме при линиях, заданных параметрически, я обратил ваше внимание на тот факт, что параметрические уравнения могут «прорисовывать» кривую АВ как слева направо, так и справа налево, из-за чего во втором случае «вылезает минус» и возникают небольшие технические затруднения. В рассматриваемой задаче мы от этого избавлены! Так как подынтегральная функция, как и в первом пункте, неотрицательна
/(-ДО) + (>’?(0) > 0 то заранее можно утверждать, что результата со знаком
«минус» получиться не ДОЛЖНО (ПОНЯТНО, при условии ^ ~£ ).
Однако вместо «вопроса прорисовки дуги» у нас появляется другая почётная обязанность — беречь неотрицательность подынтегральной функции, как зеницу ока:
Пример 4
х = 7cos t я
■ = 1
— <t<n
sm t
Вычислить длину дуги кривой Решение: аналитические условия задают левую верхнюю дугу астроиды. Причём параметрические уравнения «прорисовывают» эту кривую справа налево, но, как я только что отметил, сейчас нас это не волнует, и асфальтный каток едет дальше.
Используем формулу Сначала найдём производные:
и упростим сумму их квадратов:
Это оптимальная во многих случаях техника решения, позволяющая не «таскать за собой» значки корня и интеграла с пределами интегрирования. Тем самым минимизируется риск что-нибудь потерять в громоздкой записи. Гораздо удобнее «зарядить» в формулу готовую сумму:
А вот теперь самый важный момент. Здесь нельзя «машинально» избавляться от корня и необходимо придерживаться следующего правила:
-Ju2(0 =u(t)
,¡u2(t) =-li(t)
, если функция u<¿’} на промежутке ^’t2
или
, если — 0 на данном промежутке.
Эта «развилка» сохраняет неотрицательность подынтегральной функции что соответствует геометрическому смыслу задачи.
7Г
На отрезке
-; л»
sin í> 0, cosí <0
, следовательно, их произведение ^/(sin í cosí)2 = — sin £ cosí
Не понимаете, почему sm 1 ~ cosí ~ 0 ? Посмотрите на их графики. Продолжаем, а точнее, заканчиваем решение:
и(С = sin ■ cosí i 0
неположительное: v} и поэтому
1 = — ед.=,5ед. Ответ: 2
Приятно, когда знаешь график функции, но вдвойне приятнее, когда можно эффективно проверить или даже заранее узнать ответ. Длина астроиды
равна . В нашей задаче ^_ 7 и мы рассчитали длину «четвертинки»:
4 4 , что и требовалось проверить.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Тренируемся самостоятельно: Пример 5
Вычислить длину дуги кривой с точностью до двух знаков после запятой
Примерный образец оформления задачи и в конце урока. Продолжаем динамично закатывать асфальт:
Как найти длину дуги кривой, если линия задана в полярной системе координат?
Пусть кривая -АВ задана в полярных координатах уравнением г ^ где и ПрИ этом значение (Р~а определяет точку а значение $ —
точку £. Если на промежутке ^ ^ функция имеет непрерывную
г'(<Р)
производную г , то длина кривой -&В выражается следующей формулой:
Условие ‘ логично и незыблемо. Это третья, похожая на
предыдущую формула, которую мы незамедлительно оприходуем: Пример 6
Вычислить длину дуги кривой, заданную в полярной системе координат Порядок и принципы решения точно такие же.
Используем формулу Найдём производную по «фи»:
Составим и максимально упростим подкоренное выражение: Заливаем топливо:
презабавно, всё время понижали-понижали степень, а теперь её надо
повысить. Используем формулу двойного угла
и
■ 2 Ф 2<P
1= SHI — +COS —
основное тригонометрическое тождество самым заветный квадрат:
выцыганив тем
Теперь нужно разобраться с функцией 2 2 на отрезке
чтобы правильно избавиться от корня. Я мысленно представляю график и вижу, что функция здесь положительна, но это очевидно далеко не всем, и в этой ситуации можно использовать нечто похожее на метод интервалов. Вычислим значение функции в какой-нибудь промежуточной точке, например,
посерединке в точке
любой точке интервала ^ 0 » . К слову, и на концах тоже.
Примечание: строго говоря, надо ещё добавить, что уравнение
2 2 не имеет корней на данном интервале. Таким образом, вынесение из-под корня проходит без всяких последствий. …Не хотел вам рассказывать об одном нехорошем методе решения, но таки поделюсь — всё равно догадаетесь, по себе знаю =) На черновике считаем
интеграл 6 и если получился отрицательный результат, то
на чистовике ставим перед интегралом «минус». И никаких запарок с рассуждениями.
L = 6-У2 ■ [ cos — + sin — -11 ей. и 1,9 ед.
я
Ответ:
12
12
Я решил эту задачу много лет назад именно таким способом и недавно, подбирая примеры к уроку, нашёл более симпатичное решение, идея которого
состоит в использовании формулы приведения ^2 ^ и
дальнейшего повышения степени по избитой формуле 1-со£2^=2зттам получается ответ в другом виде, но численно результаты совпадают. Такое тоже бывает.
Затем я углубился в свой архив и нашёл ещё много чего знакомого. Такое впечатление, что сборник Кузнецова — очень популярный поставщик задач по приложениям определённого интеграла в контрольные работы. И в разделе IV-Интегралы вы можете найти порядка сотни прорешанных примеров по теме (Задачи 17-19), велика вероятность, что найдётся и ваш пример!
Успокоительная миниатюра для самостоятельного решения:
Пример 7
Вычислить длину дуги кривой, заданную в полярной системе координат
Решения и ответы:
Пример 2: Решение: пределы интегрирования: Из условия
следует, что требуется вычислить длину дуги верхней ветви у ~ .
Найдём производную: По формуле:
Ответ:
Пример 3: Решение: найдём производную: I , /н I 1 ,■ I sm у
Ху{.У) — (Ь cosjb —(cosу) — — -tgy
cos у
cos у
Таким образом:
(1) Используем тригонометрическую формулу cos y
(2) При вынесении из-под корня необходимо, чтобы подынтегральная
j^-UL -1
|| QQg у л л л %1
функция осталась положительной: ‘ 1
СОЗ.У
>0
Так как cos^ на отрезке
интегрирования, то: статьи Сложные интегралы
Ответ:
. (3) Данный интеграл разобран в Примере 18
Пример 5: Решение: используем формулу Найдём производные:
Таким образом:
Примечание: — 0 при любом значении 1. Ответ:
Пример 7: Решение: используем формулу:
Ответ’ £ = 2) ед. и 9,21 ед.
Использованная литература
1. Киселёв, Андрей Петрович // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969-1978.
2. Андронов И. К., А. П. Киселев. [Некролог], «Математика в школе», 1941, № 2
3. Маргулис А. Я., Андрей Петрович Киселев, «Математика в школе», 1948, № 4
4. Депман И. Я., История арифметики, М., 1959.
5. Моргулис А. Я., Тростников В. Законодатель школьной математики // Наука и жизнь. 1968. № 1
6. Пыльнев-Рогачёв, Лунёва М. И. Служитель «царицы-наук» // Кольцовский сквер. 2002. № 3
References
1. Kiselev, Andrey Petrovich // Great Soviet Encyclopedia: [in 30 volumes] / Ch. ed. A.M. Prokhorov. — 3rd ed. — M.: Soviet Encyclopedia, 1969-1978.
2. Andronov I.K., A.P. Kiselev. [Obituary], «Mathematics at School», 1941, no.
2
3. Margulis A. Ya., Andrey Petrovich Kiselev, «Mathematics at school», 1948,
no. 4
4. Depman I. Ya., History of arithmetic, M., 1959.
5. Morgulis A. Ya., Trostnikov V. Legislator of school mathematics // Science and life. 1968. No. 1
6. Pylnev-Rogachev, Luneva MI Servant of the «queen of sciences» // Koltsovsky square. 2002. No. 3

![1_5254fef39271a5254fef392758[1] 1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png)