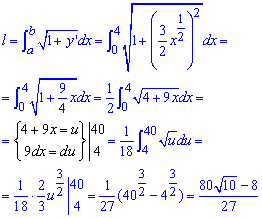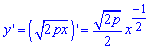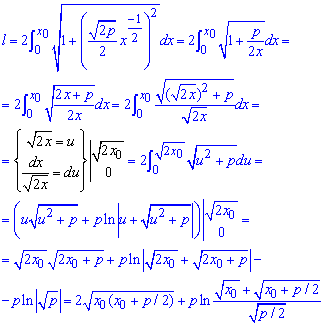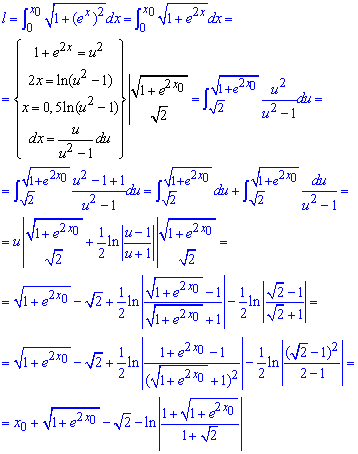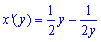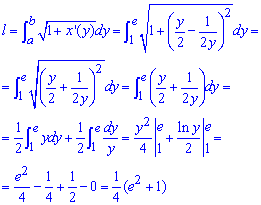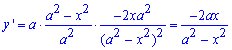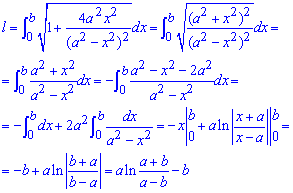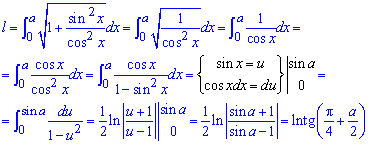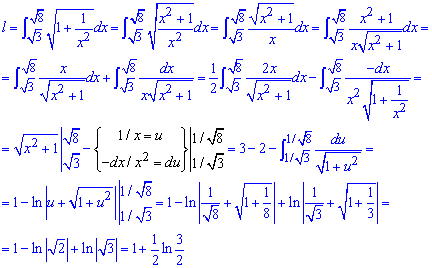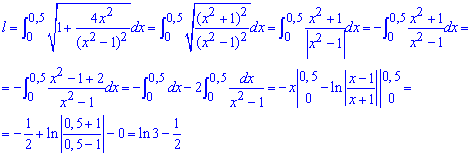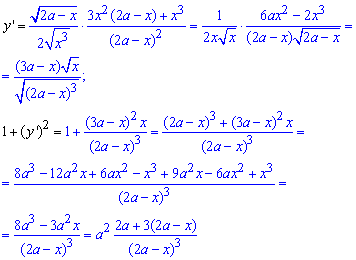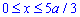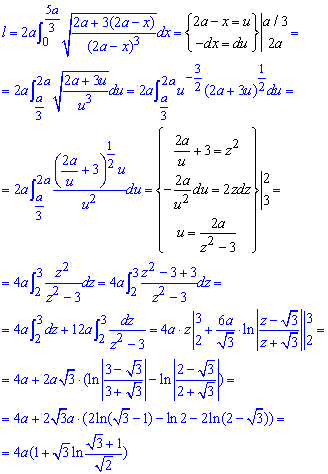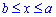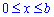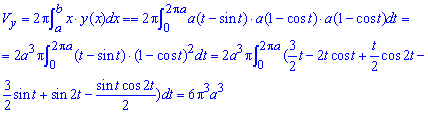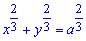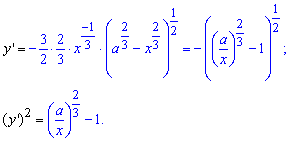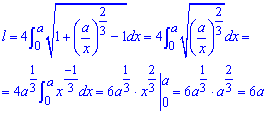Как найти длину кривой по функции

При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.

Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.

Как вычислить длину кривой

Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).

Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).

Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).

Примеры:

Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.

Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную

Применим схему I (метод сумм).

1. Точками х₀ = а, х₁…, х_n = b (х₀ < x₁ < …< х_n) разобьем отрезок [а; b] на n частей (см. рис. 183).  Пустьэтим точкам соответствуют точки М₀ = А, M₁,…,M_n =В на кривой АВ. Проведем хорды М₀M₁, M₁M₂,…, М_n-1М_n, длины которых обозначим соответственно через ΔL₁, AL₂,…, ΔL_n. Получим ломаную M₀M₁M₂ … M_n-ιM_n, длина которой равна L_n=ΔL₁ + ΔL₂+…+ ΔL_n =

2. Длину хорды (или звена ломаной) ΔL₁ можно найти по теореме Пифагора из треугольника с катетами Δx_i и Δу_i:

По теореме Лагранжа о конечном приращении функции Δу_i=ƒ'(с_i)•Δх_i, где ci є (x_i-1;x_i). Поэтому

а длина всей ломаной M₀M₁… М_n равна

3.Длина l кривой АВ, по определению, равна

.

Заметим, что при ΔL_i→0 также и Δx_i →0 ΔLi =и, следовательно, |Δx_i|<ΔL_i).

Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δx_i→ 0:

Таким образом,или в сокращенной записи l =

Если уравнение кривой АВ задано в параметрической форме

где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,

Пример 2. Определить длину окружности x² + y² = r². Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда,следовательно,

Длина всей окружности L = 2πr.

Пример 3. Найти длину дуги кривой y² = x³ от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x^1/2, откуда

Пример 4.     Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).

     Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).

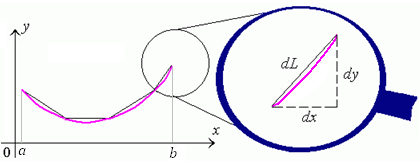
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.

      Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:

(1)

где y ‘  – производная функции y = f(x)  по переменной x.

      Длина дуги равна сумме длин составляющих ее элементов:

.

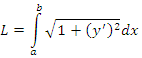Пример 5.

Вычисление
длины дуги кривой в декартовых координатах.Введем понятие длины дуги. Пусть на
плоскости введена кривая, являющаяся
графиком непрерывной функциина отрезке.
Разобьем отрезокточками наnчастей.
Из каждой точкивосстановим перпендикуляр к осиOx;
тогда дугаABразобьется
наnчастей точками(рис.4). Заменим каждый участок дугиучастком прямой.

Определение.Длиной дуги называется пределL,
к которому стремится длина ломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон,
а значит, и при,
т.е.

(8)

Рис. 4 Рис.5

Пусть
функция
и ее производнаянепрерывны на отрезке.
Согласно теореме Пифагора имеем.
Обозначим.
Так каки,
то на основании теоремы Лагранжа получим

.

Тогда
.
В следствие непрерывности производнойсуществует предел (8) интегральной суммы.
Таким образом,

(9)

По
определению предел (9) равен определенному
интегралу от функции
на отрезке:

.
(10)

Это и
есть формула для вычисления длины дуги.

Пример
4. Найти длину дуги кривой
,
отсеченной прямой(рис.5).

Решение.
Найдем производную функции y=f(x),
заданной неявно соотношением;
имеем,
откудаВ силу симметрии достаточно вычислить
длину половины кривой.
По формуле (10) получим

,
при.

Вычисление
дуги плоской кривой, заданной в
параметрической форме. Рассмотрим
параметрически заданную кривуюгде— непрерывные и имеющие непрерывные
производные функции, причем.
Пусть.
В интеграле (10) произведем подстановку;
так как,
то получим

.
(11)

Пример
5. Найти длину окружности радиуса R.

Решение.
Уравнения окружности в параметрической
форме имеют вид
Найдем четвертую часть длины окружности.
По формуле (11) имеем

Что
согласуется с общеизвестным результатом.

Вычисление
длины дуги плоской кривой в полярных
координатах.Воспользуемся формулами
перехода от полярных координат к
декартовым:(учли,
что радиусrесть функция
полярного угла). Эти уравнения можно
рассматривать, как параметрические
уравнения кривой при изменении параметрав пределах.
Тогда по формуле (11) находим

.
(12)

3. Вычисление объемов и площадей поверхностей вращения.

Пусть
криволинейная трапеция, ограниченная
графиком непрерывной функции y=f(x),
осьюOxи прямымиx=a,x=b, вращается
вокруг осиOx.

(рис.6)

Найдем
объем Vполученного тела
вращения. Ясно, что произвольное
поперечное сечение этого тела представляет
собой круг. Площадь круга, образованного
при сечении тела вращения плоскостьюx=x, есть.
Тогда используя формулу,
получим

(13)

Если
криволинейная трапеция, ограниченная
непрерывной функцией
,
осьюOyи прямымиy=aиy=b, вращается
вокруг осиOy, то объем
полученного тела вычисляется по формуле

(14)

Пример
6. Найти объем конуса с радиусом основания
Rи высотойh.

Решение.
Конус можно считать телом, полученным
вращением прямоугольного треугольника
с катетами hиRотносительно осиOx. Найдем
уравнение гипотенузы этого треугольника.
Имеемy=kx,
где.
По формуле (13) получим

Вычисление
площади поверхности тела вращения.

Определение.Площадью поверхности
тела, полученного при вращении дугиABвокруг осиOxназывается
предел,
к которому стремится площадь поверхности,
образованной вращением вокруг осиOxломаной,
вписанной в дугуAB, при
стремлении к нулю наибольшей из ее
сторон,
а значит, и при,
т.е..

Формула для вычисления площади поверхности
вращения вокруг оси Ox

(15)

Если
кривая вращается вокруг оси Oy,
то формула имеет вид

(16)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  02.04.2015132.61 Кб1013.doc

• #
• #

  02.04.2015310.78 Кб6014.doc

• #
• #
• #

  02.04.2015390.66 Кб2316.doc

• #
• #
• #
• #
• #

Длина дуги кривой

Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича). 

Для запоминания основных моментов схема интегрирования и вычисление дуги кривой из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы графиками кривых.

Найти длины дуг кривых в прямоугольной системе координат

Пример 2.117 (2431) Вычислить длину дуги кривой y=x^3/2 (полукубическая парабола Нейля) xє[0;4] .
Вычисление: Найдем производную заданной функции по переменной x:

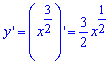
График полукубической параболы Нейля имеет вид

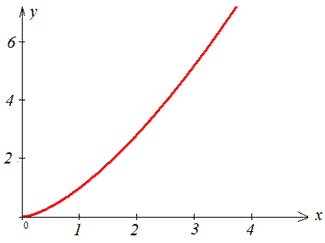
Выписываем пределы интегрирования:
a=0, b=4 (известны из начального условия).
По формуле находим длину дуги на заданном отрезке:

Во время интегрирования для приведения подынтегральной функции к табличному виду выполнили замену переменных.
При этом нужно перечислять пределы интегрирования.
В результате пришлось интегрировать корневую функцию, а длина дуги после вычислений приблизительно равна l=9,07.
Помните, что все длины измеряются в единицах (од.) !!!

Пример 2.118 (2432) Найти длину дуги кривой y²=2px (парабола) xє[0;x₀].
Вычисление: Поскольку отрезок дуги параболы задан в пределах [0;x₀], то заданная функция будет иметь вид положительной ветки корневой функции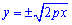  
Вычислим производную функции по переменной x:

Запишем пределы интегрирования:
a=0, b=x₀ . 

График параболы приведен ниже

Вычислим длину дуги через определенный интеграл:
для сведения к простым формулам интегрирования применяем замену переменных, при этом не забываем перечислить изменение пределов интегрирования:

В конце вычислений применено интегрирование частями.

Пример 2.119 (2434) Найти длину дуги кривой y=e^x, [0;x₀].
Вычисление: Для интегрирования находим производную (по переменной x) экспоненты :
y’=(e^x)’=e^x.
Поскольку показатель не содержит никаких коэффициентов при переменной, то производная равна самой экспоненте.
Из начального условия выписываем пределы интегрирования:
a=0, b=x₀.
График экспоненты имеет вид

Чтобы вычислить длину дуги экспоненты переходим к новой переменной.
Это ведет к изменению и пределов интегрирования и самого дифференциала:

Напоследок расчетов приходим к формуле дуги, которая содержит корневую и логарифмическую зависимости от бегущей координаты.

Пример 2.120 ( 2435) Найти длину дуги кривой x=1/4y²-ln(y)/2, yє[1;e].
Вычисление: Вычислим производную (по переменной y ) заданной функции:

Приведенная формула работает и для обратных функций x=x(y), особенно если функция изменяется как показано на графике

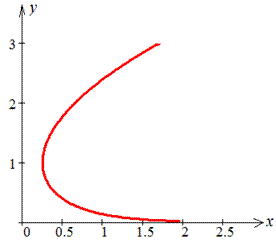
Пределы интегрирования: a=1, b=e .
Находим длину дуги кривой на заданном отрезке:

При возведении к квадрату производной получим простую для интегрирования функцию, которая в результате дает l=(e²+1)/4.

Пример 2.121 (2436) Вычислить длину дуги кривой

Вычисление: Найдем производную по переменной x функции:

Пределы интегрирования для этой дуги равны [0;b].
График исследуемого логарифма имеет вид

Интегрированием находим длину дуги кривой:

Со всеми превращениями подинтегральной функции попробуйте разобраться самостоятельно.

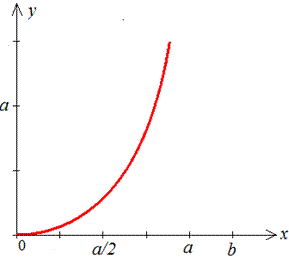
Пример 2.122 (2437) Вычислить длину дуги кривой y=ln(cos(x)), 0<x<a<Pi/2.
Вычисление: Найдем производную (по переменной x) заданной функции :

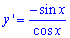
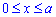
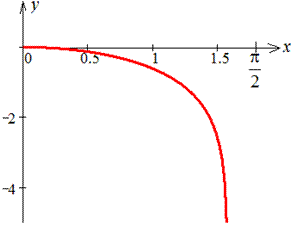
Запишем пределы интегрирования: (известны за условием).

Вычислим длину дуги кривой на заданном отрезке:

Если воспользоваться тригонометрическими формулами то перейдем к тангенсу, а сама длина дуги равна
l=ln(tg (Pi/4+a/2)).

Пример 2.123 Найти длину дуги кривой y=ln(x),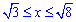
Вычисление: Вычисляем производную от логарифма:
y’=1/x.
Пределы интегрирования переписываем из условия: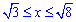
 
График логарифма имеет вид

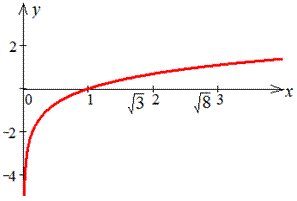
Интегрирование по длине дуги достаточно непростое, требует добрых умений.
Расписав подынтегральную функцию, и применив замену переменных к одному из интегралов, приходим к логарифмам, которые при указанных пределах интегрирования несколько упрощаются.

Невзирая на трехэтажные выражения конечное значение длины дуги выраженно простой зависимостью.

Пример 2.124 Найти длину дуги кривой y=ln(1-x₂), x[0;0,5].
Вычисление: Найдем производную (по переменной x) заданной функции :

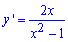
Из начального условия имеем такие пределы интегрирования: [0;0,5].
График исследуемого логарифма имеет вид

Вычисляем длину дуги логарифма:

Если округлить конечное значение, то будем иметь l=0,5986.

Пример 2.125 (2439) Вычислить длину дуги кривой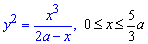  
Вычисление: Поскольку график заданной функции симметричен относительно оси Ox, то вычислим длину дуги для положительной части функции

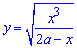
и результат умножим на 2.
Найдем производную функции и саму подинтегральную функцию:

Пределы интегрирования известны:

График веток в декартовой плоскости имеет вид.

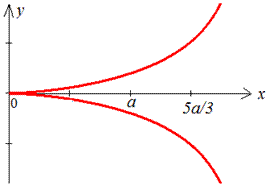
При нахождении длины дуги дважды выполняем замену переменных.
Как и в предыдущих примерах ответ получаем через логарифмы

Кому в учебе придется вычислять подобное задание, просьба разобраться с превращениями.
А еще лучше — придумать и решить подобный пример.

Пример 2.126 (2438) Найти длину дуги кривой 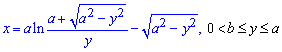(трактриса).
Вычисление: Запишем производную по переменной y трактрисы (см. 2408):

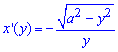
Пределы интегрирования:

График трактрисы имеет вид

По формуле дуги кривой интегрируем и находим длину трактрисы:

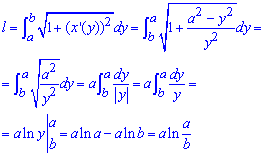
Конечная формула достаточно простая для расчетов.
От края следует несколько отойти, в ином случае длина трактрисы направляется к безконечности.

Пример 2433 Найти длину дуги кривой 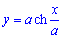(цепная линия) от точки A(0;a) к точке B(b;h) .
Вычисление: Цепная линия — это кривая, форму которой принимает цепь (нить) под действием силы притяжения, которая подвешена за оба конца.
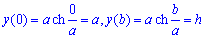
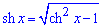
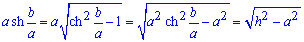
Поскольку и , то

Найдем производную трактрисы:

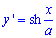
Пределы интегрирования по аргументу следующие:

Рисунок цепной линии приведен ниже

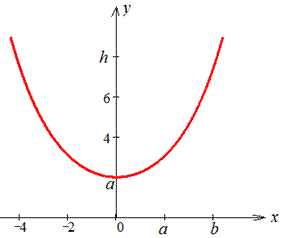
Вычислим длину дуги кривой на заданном отрезке:

Пример 2440 Найти длину дуги астроиды
Вычисление: Для астроиды оси прямоугольной системы координат делят линию на 4 части (смотри 2429), поэтому длину будем искать для чверти и результат умножим на 4.
Выражаем функцию для чверти астроиды

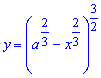
Найдем производную от полученной зависимости и подинтегральную функцию:

Пределы интегрирования: [0;a] (для чверти астроиды).
Вычислить длину дуги астроиды на практике достаточно легко:

Дело в том, что единицы сокращаются и получаем простой табличный интеграл.
В результате длина астроиды равна l=6a.

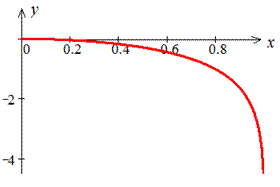
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции
:

Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо
вычислить определенный интеграл:

В более общем случае, если у нас задана функция

в декартовых координатах и стоит задача найти длину дуги этой кривой между точками

и
,
нам необходимо вычислить интеграл:

В приведенной выше формуле, выражение

означает, что сначала нужно вычислить производную функции
,
а затем полученное выражение возвести в квадрат.

Наш онлайн калькулятор позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.