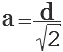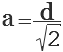/
/
/ Длина стороны квадрата
Длина стороны квадрата
Установить Длина стороны квадрата на мобильный
Найти длину стороны квадрата
зная площадь
|
||
| Площадь квадрата S | ||
|
|
||
| Результат |
Вычислить длину стороны квадрата
зная диагональ
|
||
| Диагональ квадрата d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.5 (Голосов 24)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного | Стороны равнобедренного | Стороны равностороннего |
| Стороны прямоугольника | Стороны ромба | Стороны параллелограмма | Ребро куба |
Александра
532 дн. назад
Клас клас клас!!! Не могла понять (сломала голову
- reply
Наталья
829 дн. назад
Класс!!! Не люблю считать. Вообще… Спасибо!!!
- reply
Николай
1028 дн. назад
Супер. И быстро. Мне нравится.
- reply
Добавить комментарий:
Я не робот
Где d — диагональ квадрата.
Где S — площадь квадрата
Где r — радиус вписанной окружности
Где R — радиус описанной окружности
Где P — периметр квадрата.
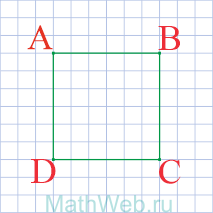
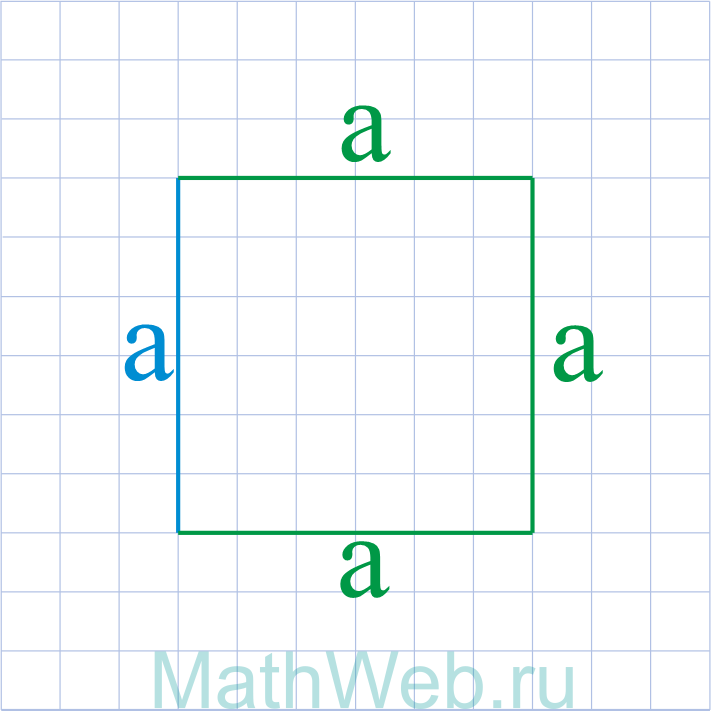
- Квадрат — это четырехугольник у которого все стороны равны AB = BC = CD = DA.
- Противоположные стороны квадрата параллельны, а смежные — перпендикулярны.
- Все квадраты отличаются между собой только длиной стороны.
Как найти длину стороны квадрата?
Сторона квадрата может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = |
 |
a = √S |
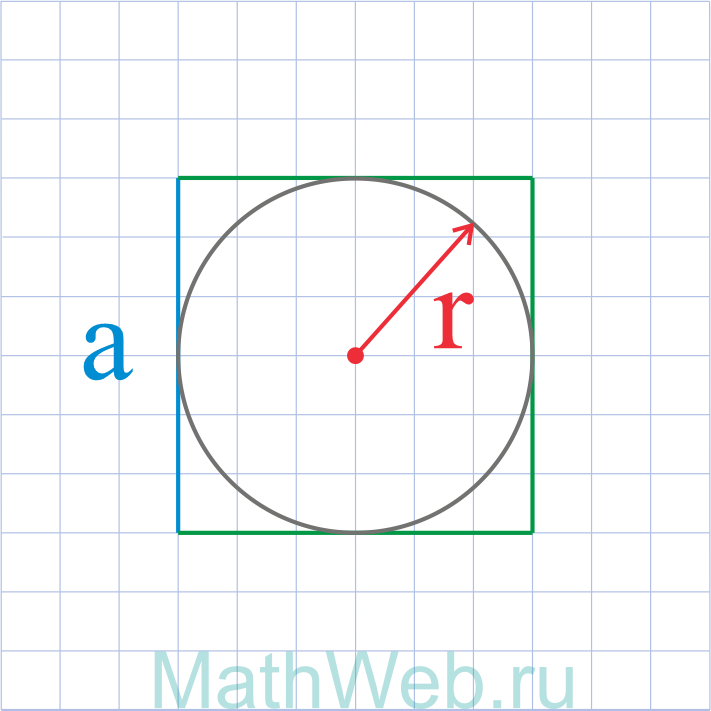 |
a = 2r |
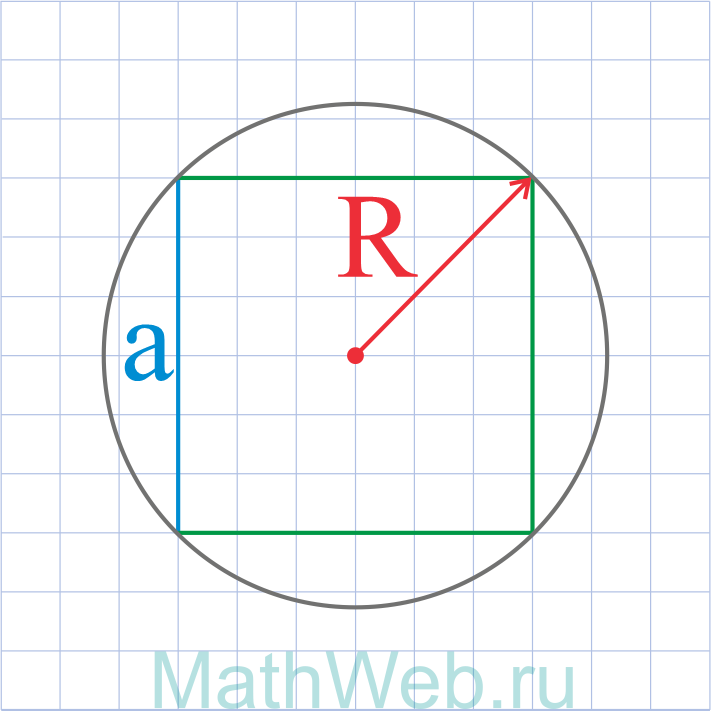 |
a = R√2 |
 |
a = |



Найти длину стороны квадрата зная площадь или диагональ
Калькулятор производит расчёт длины стороны квадрата зная площадь или диагональ.
Найти длину стороны квадрата зная площадь
Формула расчёта длины стороны квадрата зная его площадь Вам необходимо указать площадь квадрата (S). Расчёт происходит по формуле a=[квадратный корень](S).
Извлекаем квадратный корень из площади.
| Площадь квадрата (S) |
Найти длину стороны квадрата зная диагональ
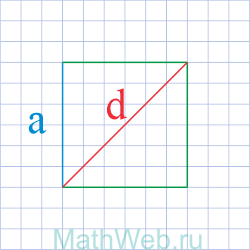
Формула расчёта длины стороны квадрата зная его диагональ Вам необходимо указать диагональ (d). Расчёт происходит по формуле a=d/[квадратный корень](2).
Диагональ делим на квадратный корень из двух.
| Диагональ квадрата (d) |
Периметр прямоугольника (квадрата)
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
Как найти сторону квадрата?
Часто в геометрии необходимо найти длину стороны квадрата, при этом известны такие его параметры: периметр, площадь, длина диагонали.
Квадрат — это ромб или прямоугольник, стороны которого равны между собой. Углы квадрата также равны между собой и имеют по 90° каждый. Рассмотрим, как найти сторону квадрата имея один из вышеперечисленных параметров.
Нахождение стороны квадрата по его периметру
В этом случае, чтобы найти длину стороны квадрата, необходимо число значения периметра квадрата разделить на 4 (поскольку квадрат имеет 4 стороны, равные между собой): z = P/4, где z — это длина стороны квадрата; P — это периметр квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его периметра. Например, если задан периметр квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задан периметр квадрата 40 метров. При решении этой задачи мы получим: z = 40/4 = 10. Длина стороны квадрата — 10 метров.
Нахождение стороны квадрата по его площади
В этом случае, чтобы найти длину стороны, необходимо добыть квадратный корень числа значения площади (поскольку площадь квадрата равна квадрату его стороны): z = vS, где z — это длина стороны квадрата; S — это площадь квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его площади. Например, если задана площадь квадрата в миллиметрах квадратных — длина его стороны будет просто в миллиметрах.
Например: Задана площадь квадрата 16 квадратных метров. При решении этой задачи мы получим: z = v9 = 3. Длина стороны квадрата — 4 метра.
Нахождение стороны квадрата по его диагонали
В этом случае длина стороны квадрата будет равна длине диагонали квадрата, разделенной на корень квадратный из 2 (за теоремой Пифагора, поскольку смежные стороны квадрата и его диагональ составляют равнобедренный прямоугольный треугольник). Чтобы найти сторону квадрата по диагонали необходимо: z = d/v2 (так как z 2 + z 2 = d 2 ), где: z — это длина стороны квадрата; d — это длина диагонали квадрата.
Единицей измерения одной стороны квадрата будет та же самая единица измерения длины, как у его диагонали. Например, если задана диагональ квадрата в миллиметрах, то также длина его стороны будет в миллиметрах.
Например: Задана диагональ квадрата 20 метров. При решении этой задачи мы получим: z = 20/v2, это приблизительно равно 20/1,4142. Длина стороны квадрата — 20/v2 метров, или, приблизительно, 14,142 метров.
Теперь Вы знаете, как найти длину стороны квадрата, если заданы его периметр, площадь или длина диагонали.
Сторона квадрата
Квадрат, наряду с кругом, считается идеальной геометрической фигурой. Квадрат является не только параллелограммом, но и ромбом, и прямоугольником одновременно, так как у него все стороны равны и все углы прямые. Более того, квадрат является представителем ряда правильных многоугольников, поэтому к нему относятся и их свойства тоже. Вычислить сторону квадрата можно несколькими различными способами: через периметр квадрата, через площадь квадрата или через диагональ квадрата, а также радиусы вписанной и описанной окружностей.
Поскольку все стороны квадрата между собой равны, а периметр многоугольника – это сумма всех его сторон, то найти сторону можно, разделив периметр на четыре (количество равных сторон):
Площадь квадрата – это его сторона, возведенная во вторую степень, следовательно, если нам нужно найти сторону через площадь, то необходимо извлечь из нее квадратный корень:
Если дана диагональ квадрата, то исходя из теоремы Пифагора в прямоугольном треугольнике, который образует диагональ, сторона будет равна диагонали, деленной на корень из двух:
a 2 +a 2 =d 2
2a 2 =d 2
Сторона квадрата
Четырехугольник, у которого все четыре стороны равны, противоположные — параллельны, а углы — прямые, называется квадратом. Диагональ квадрата (d) делит его на 2 одинаковых прямоугольных треугольника, у которых гипотенузой является диагональ (d) квадрата, а катетами — две одинаковых стороны квадрата (а). Как известно по теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Т.е. d 2 = а 2 + а 2 = 2а 2 .
Отсюда, сторона квадрата (а) равна диагонали квадрата (d) деленной на корень квадратный из двух.
Как найти сторону квадрата, если известна его площадь
При решении геометрических задач приходится находить одни величины, если известны другие. Так, например, если заданы три стороны треугольника, то по ним можно вычислить все его остальные характеристики. Однако, зная площадь треугольника, посчитать длину его сторон (в общем случае) невозможно. А вот если известна площадь квадрата, найти его сторону очень легко.
Вам понадобится
- калькулятор или компьютер
Инструкция
Чтобы найти сторону квадрата, если известна его площадь, извлеките из числового значения площади квадратный корень. То есть найдите такое число, квадрат (вторая степень) которого равняется площади квадрата. В виде формулы данное правило записывается следующим образом:а = √S, где:а – длина стороны квадрата,
S – площадь квадрата.Длина стороны квадрата будет измеряться в соответствующих линейных единицах. Так, например, если площадь квадрата равняется 16 квадратным сантиметрам (см²), то длина его стороны будет равняться 4 сантиметрам (см).
Для того чтобы посчитать корень квадратный из числа, возьмите инженерный калькулятор (такой, где имеются обозначения математических функций). Наберите на клавиатуре калькулятора числовое значение площади квадрата. Затем нажмите на кнопку, обозначенную как «√». Числовое значение длины стороны квадрата появится на индикаторе калькулятора.
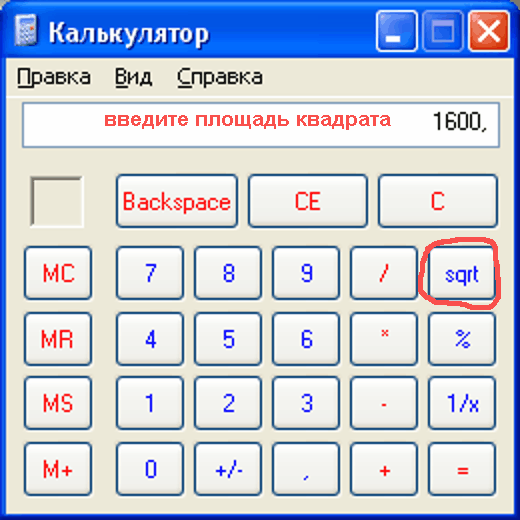
Для расчета квадратного корня на компьютере запустите стандартный калькулятор Windows. Переключите его в «обычный» (не инженерный!) вид. Затем наберите значение площади. Нажмите на кнопку, обозначенную как «sqrt».
Чтобы найти сторону квадрата с заданной площадью можно воспользоваться программой MS Excel. Для этого запустите саму программу Excel, укажите курсором на произвольную клетку таблицы и нажмите кнопку «=». Затем нажмите на появившийся значок выбора функции (fx) Выберите из предложенного списка функцию «КОРЕНЬ». После чего введите в появившееся окошко числовое значение площади квадрата и нажмите кнопку «Ок» (или клавишу «Enter»). Значение корня квадратного, а соответственно и длины стороны квадрата тут же появится в данной клетке.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.