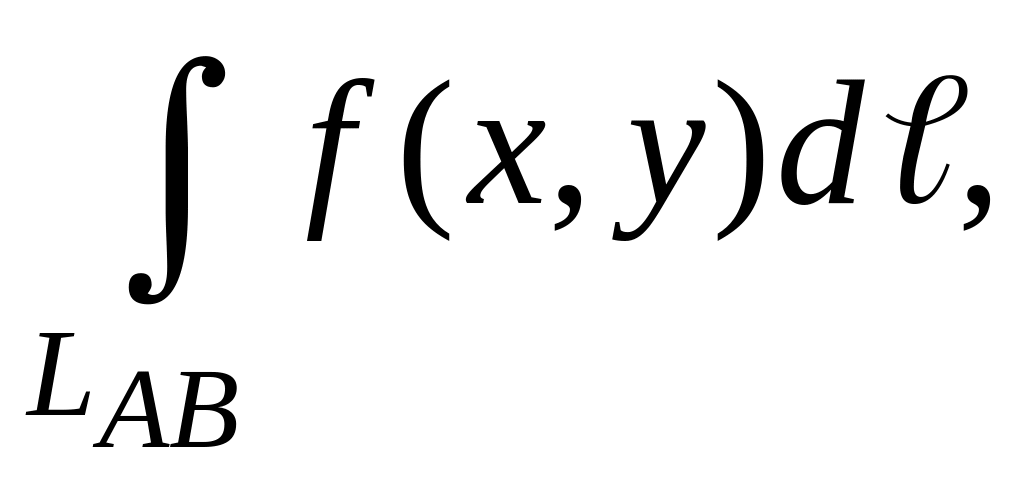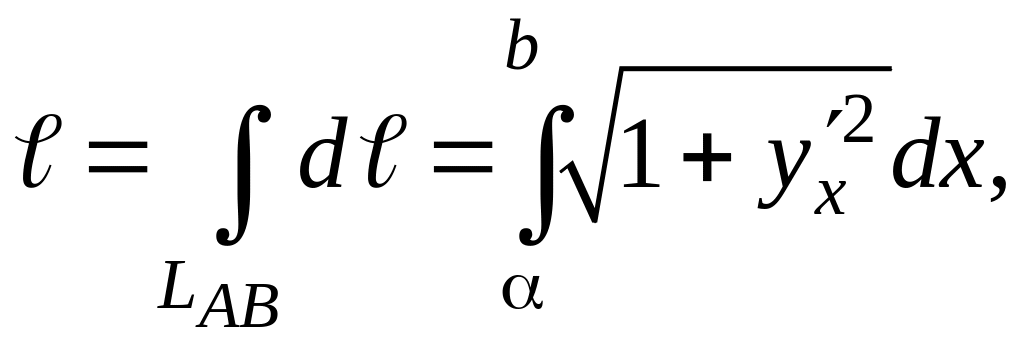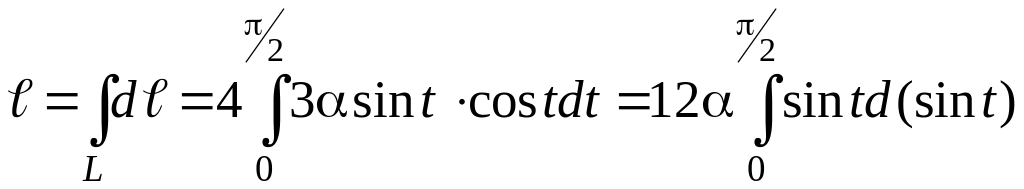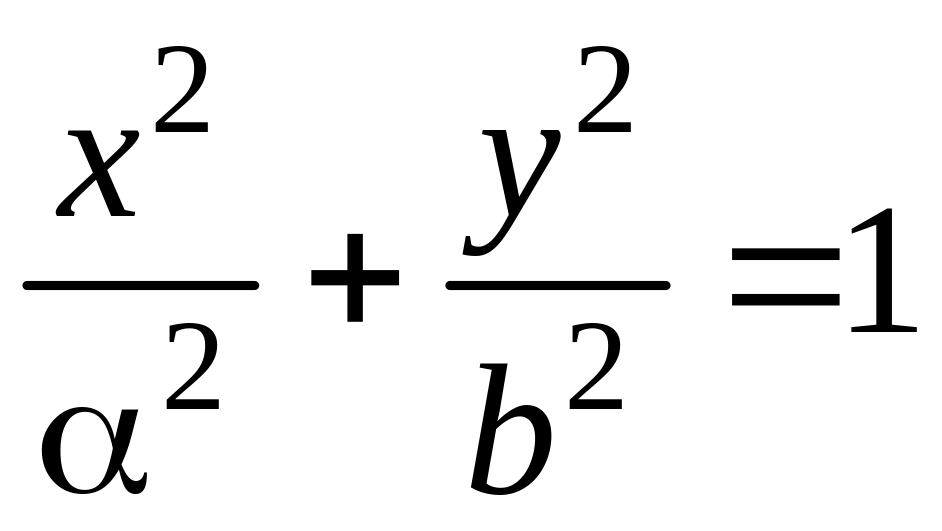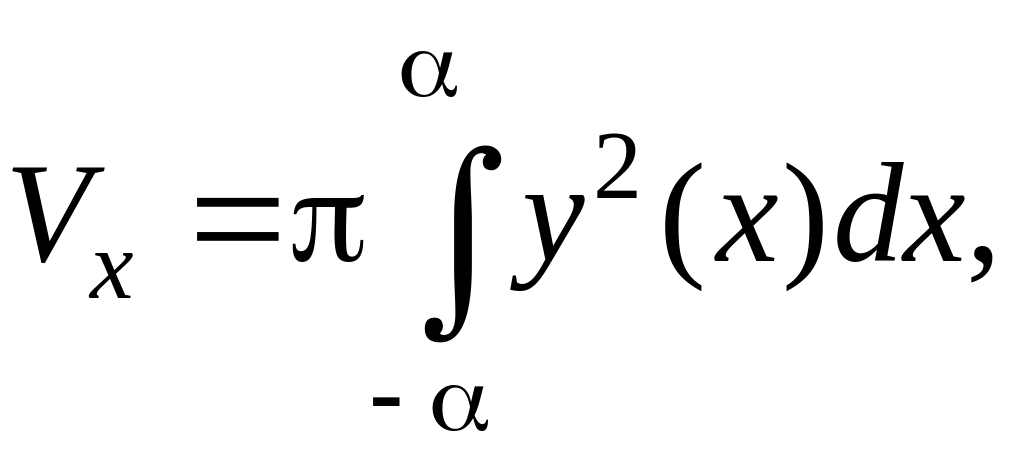Как найти длину линии через угол - Исправление недочетов и поиск решений вместе с Examum.ru

Длину
плоских кривых, заключенных между двумя
точками А
и В,
можно найти с помощью криволинейного
интеграла

если положить f(x,y)
≡ 1. В этом случае криволинейный интеграл,
также как и двойной, будет равен размерам
области интегрирования, т.е. длине части
линии L_AB.

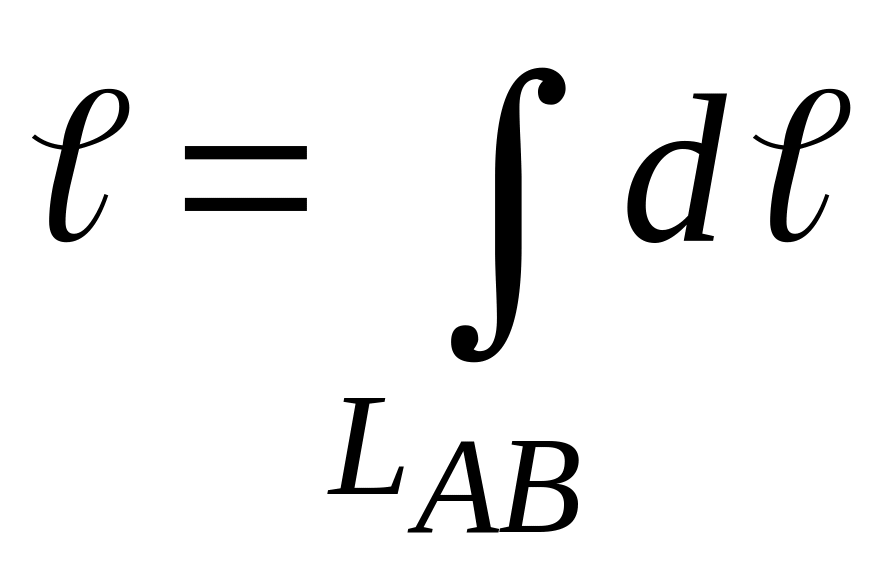
Меру
элементарной части (дифференциал длины)
— dℓ
выражают через уравнение данной линии
L_AB
и переходят к линейному интегралу. Если
кривая L_AB
задана в декартовой системе координат
непрерывной и дифференцируемой функцией
y
= y(x),
то вычисление ее длины сводят к вычислению
линейного интеграла вида:

где

Пределы
в линейном интеграле α
и b
– являются проекциями на ось Oх
точек линии А
и В
соответственно.

Длину
дуги АВ
кривой, заданной параметрическими
уравнениями x
= x(t);
y
= y(t),
находят по формуле

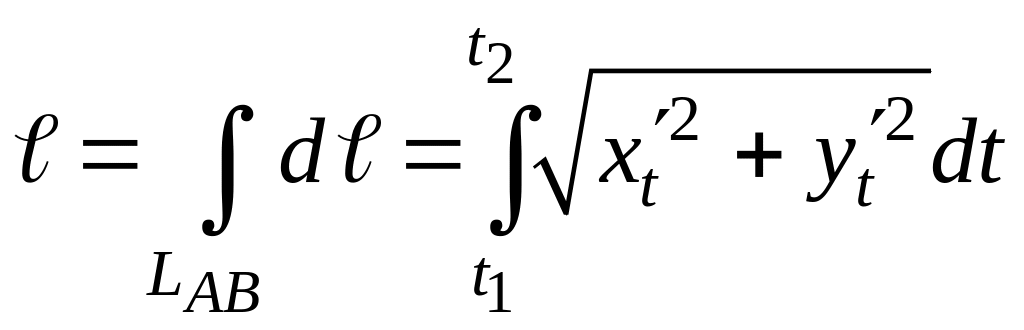
где
t₁
и t₂
значения параметра t
в точках А
и В.

И
наконец, длина линии L_AB,
уравнение которой r
= r(φ)
задано в полярной системе координат,
равна линейному интегралу

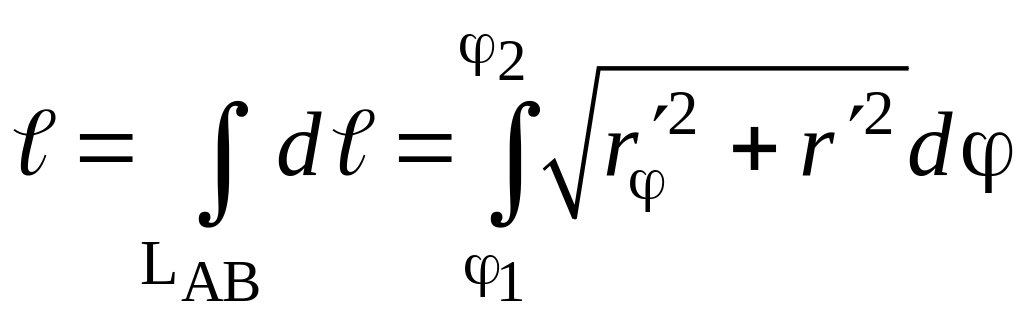
где
φ₁
и φ₂
полярные углы точек А
и В.

Пример
5. Найти длину
полукубической параболы y²
= x³
от точки А(0,0)
до точки В(4;8).

Решение.
Длина отрезка полукубической параболы
между точками А
и В
равна криволинейному интегралу

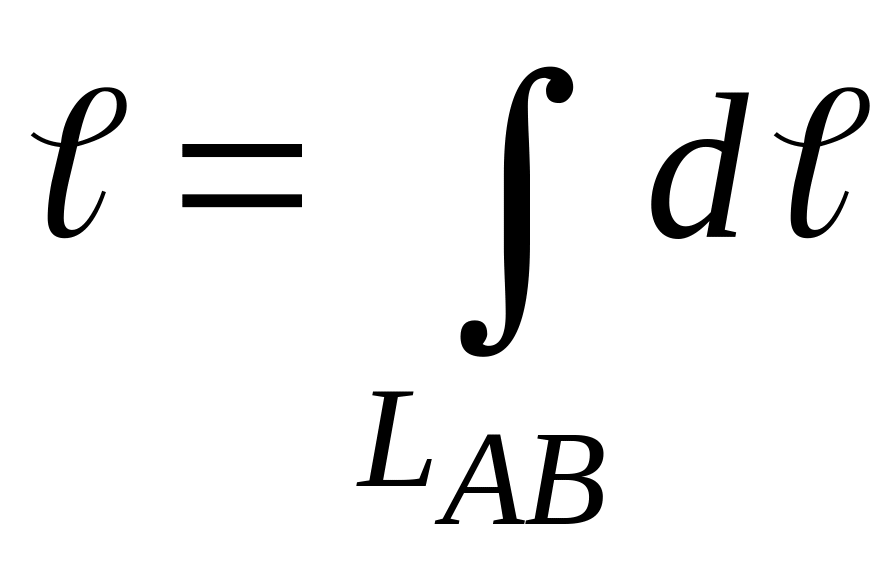
Дифференциал
длины кривой в
декартовой системе координат
выражают через ее уравнение y
= y(x)
по формуле

Найдем
его для данной линии

Переход
от криволинейного интеграла к линейному
и вычисление последнего дает искомую
длину:

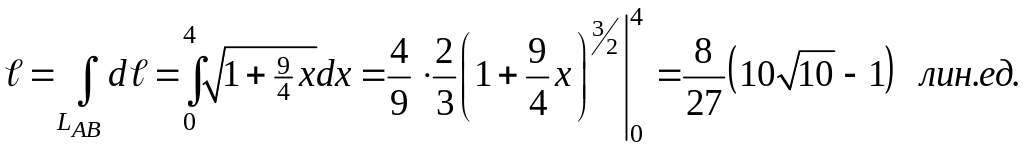
Пример
6. Найти длину
астроиды, заданную
параметрическими уравнениями

Решение.

Длину астроиды
также найдем с помощью криволинейного
интеграла

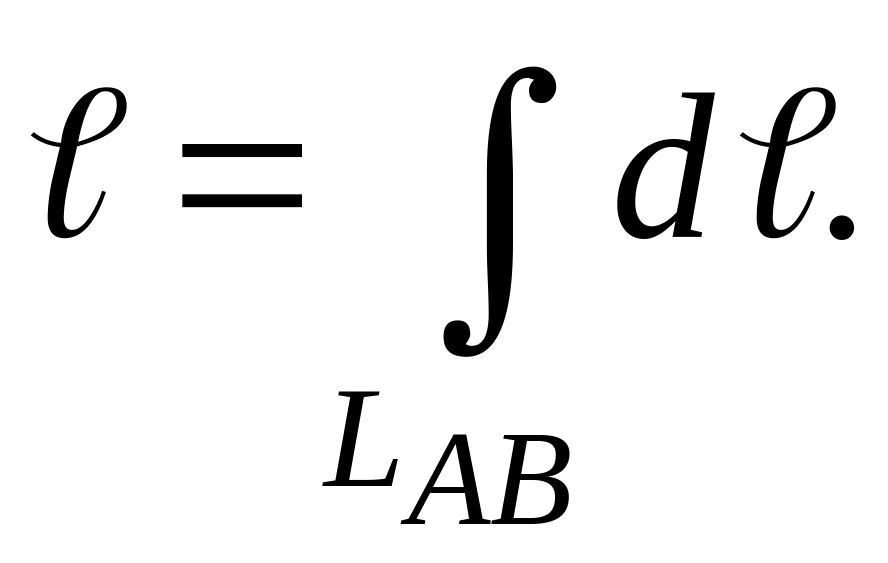
Дифференциал
длины кривой, заданной параметрически,
выражают через ее уравнение по формуле

Найдем его для
астроиды

Подставляя
найденное выражение для dℓ
в криволинейный интеграл и переходя к
линейному, получим:

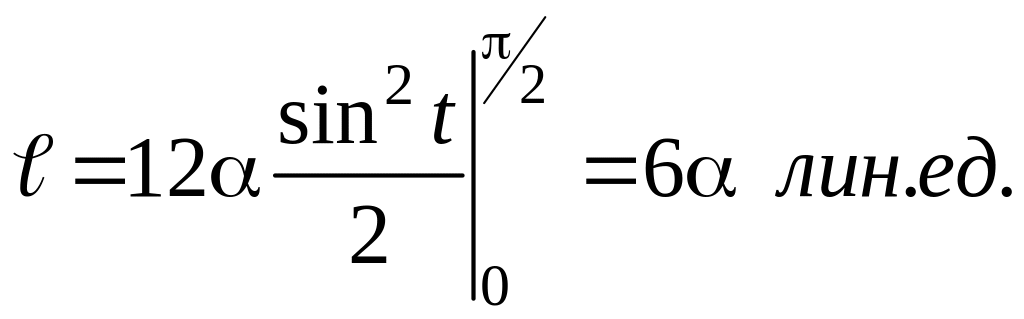
3.11.3.Вычисление объемов тел

Объем
тел, в зависимости от их формы и условий
задачи, можно находить различными
способами.В частом случае, когда известна
площадь поперечных сечений тела, его
объем вычисляют с помощью линейного
интеграла
по формуле:

где
S(x)
– площадь сечения тела плоскостью,
перпендикулярной оси Ox,
α
и b
– проекции его крайних точек на ту же
ось.

Исходя
из этой формулы, находят объем тел
вращения.

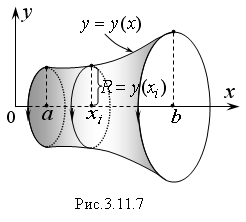
П
усть
криволинейная трапеция, ограниченная
сверху графиком непрерывной функции y
= y(x)
и прямыми x
= α,

x
= b,
вращается вокруг оси Oх
(Рис. 3.11.7).

В
результате ее вращения образуется тело.
Его плоскими сечениями, перпендикулярными
оси Oх,
являются круги с различными радиусами

R
= y(x),
площадь которых равна:

Следовательно,
объем полученного тела можно найти по
формуле

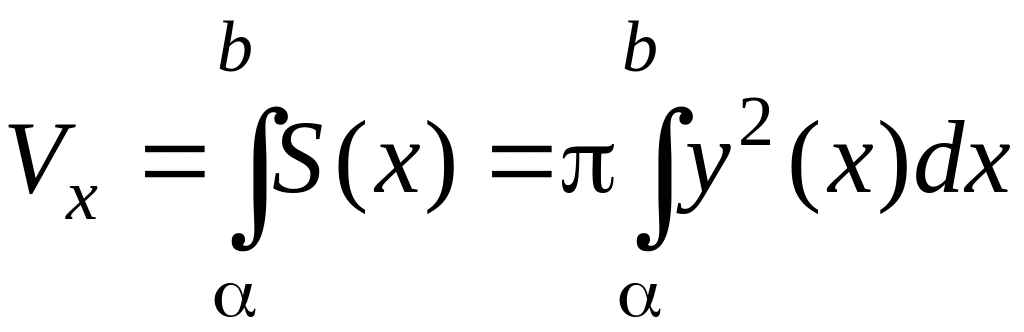
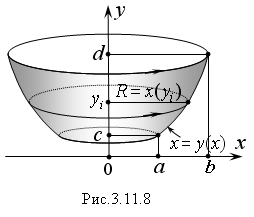
П
ри
вращении линии, ограничивающей
криволинейную трапецию, вокруг оси Oy
(Рис. 3.11.8) объем полученного тела равен:

где
x(y)
– уравнение вращающейся линии решенное
относительно переменной x.

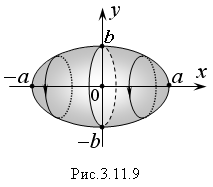
Пример
7. Найти объем
тела, полученного при вращении эллипса
относительно осей Ox
и Oy.

Р
ешение.
График эллипса

изображен на рисунке 3.11.9.

Координаты
его крайних точек по оси Oх:

x₁
= –α,
x₂
= α,
по оси Oy:
y₁
= –b,
y₂
= b.

Объем
тела, образованного вращением эллипса
относительно оси Oх,
найдем по формуле:

где

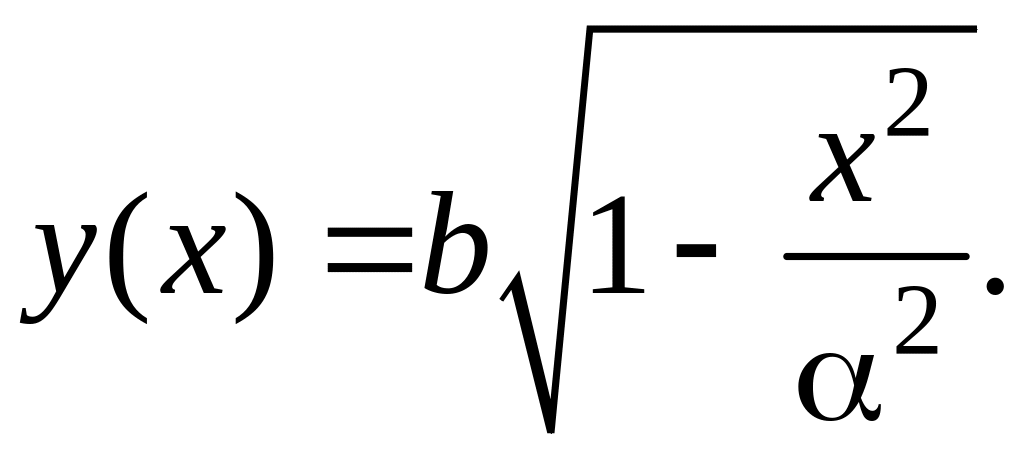
С учетом симметрии

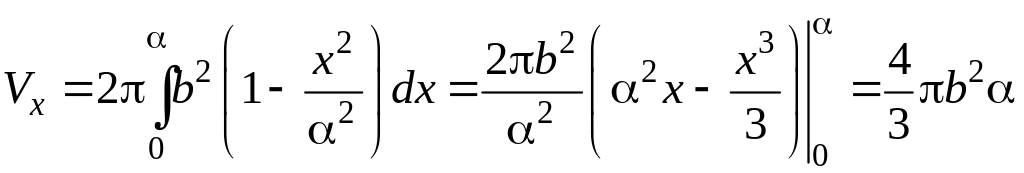
Аналогично,
вычислим объем Vy

где

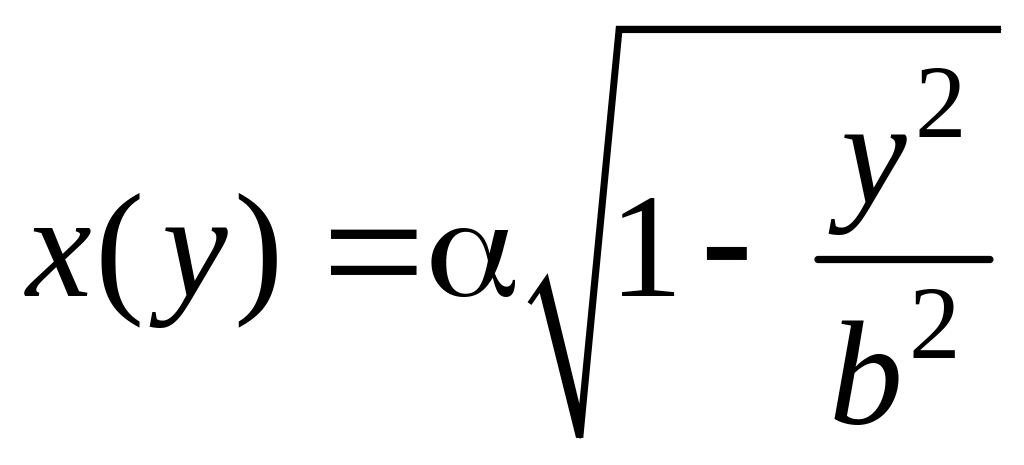
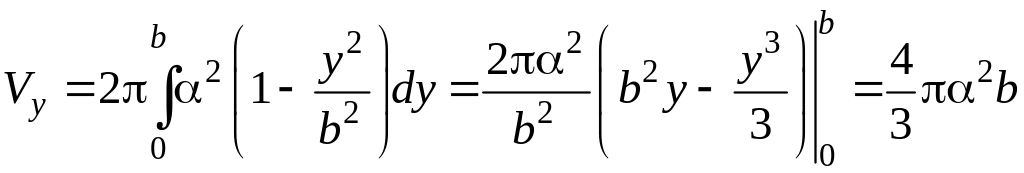
Если
α
= b,
то тела вращения относительно осей Oх
и Oy
становятся шаром, объем которого равен

.

Р
ассмотрим
теперь общий случай вычисления объемов
тел с помощью кратныx
интегралов.

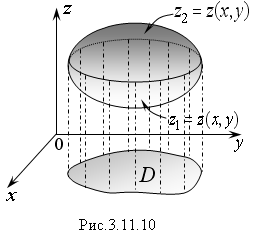
Пусть
тело произвольной формы ограничено
двумя поверхностями, уравнения которых
известны:

Проекцией данного тела на плоскость
xOy
является область D
(Рис. 3.11.10). Двойной интеграл по области
D
геометрически равен объему цилиндра,
построенного на этой области и
ограниченного сверху графиком
подынтегральной функции. Поэтому объем
тела, изображенного на рисунке 3.11.10,
можно представить как разность объемов
двух цилиндрических тел, или как разность
двух двойных интегралов:

В
самом общем случае объем тел произвольной
формы находят с помощью тройного
интеграла,
в котором подынтегральная функция равна
единице

Легко
заметить, что предыдущая формула является
следствием последней, в самом деле:

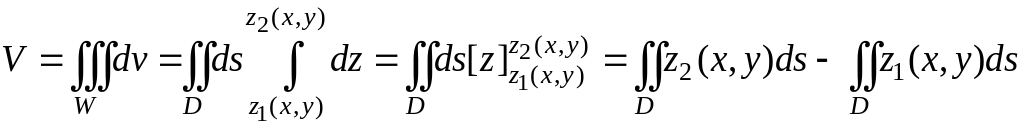
Пример
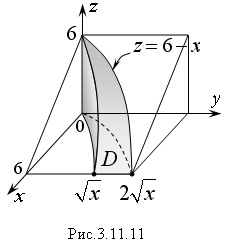
8. Найти
объем, ограниченный поверхностями:

z
= 0, z
+ x
= 6

Р
ешение.
Тело ограничено двумя цилиндрическими
поверхностями

с образующими, параллельными оси Oz,
и двумя плоскостями z
= 0, z
= 6 – x.
Искомый объем равен объему цилиндрического
тела, построенного на области D
и ограниченного сверху плоскостью z
= 6 – x
(Рис. 3.11.11). Найдем его с помощью двойного
интеграла

Переменная
x
внутри области D
изменяется от 0 до 6, а переменная y
от ее значений на линии

до значений на линии

.
Перейдем к двукратному интегрированию:

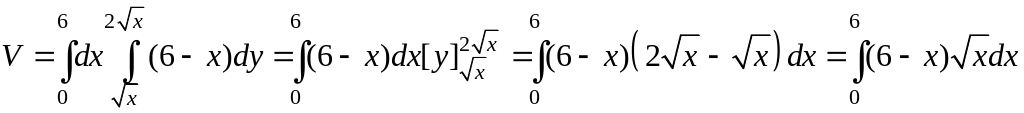
Вычисляя последний
интеграл, получим

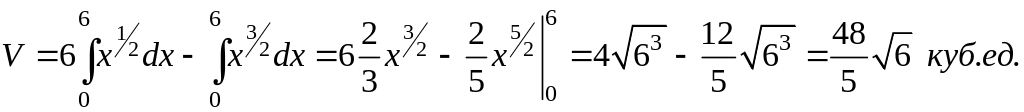
Для сравнения
найдем этот же объем с помощью тройного
интеграла

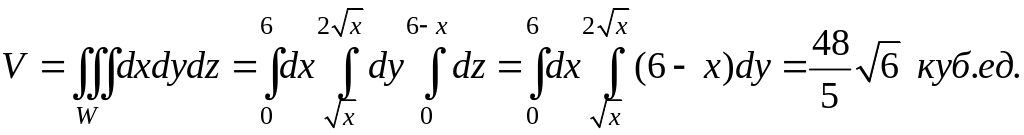
После
подстановки пределов для переменной z
мы приходим к такому же двойному
интегралу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.

Решение обратной геодезической задачи онлайн

Обратная геодезическая задача заключается в том, что при известных координатах точек А( X_A, Y_A ) и В( X_B, Y_B ) необходимо найти длину S_AB и направление линии АВ: румб r_AB и дирекционный угол α_AB

Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.

Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.

Сначала находим приращения координат:

ΔX = X_B – X_A ;

ΔY = Y_B – Y_A .

Величину угла r_AB определяем из отношения

По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим α_AB.

Для контроля расстояние S_AB дважды вычисляют по формулам:

Источник

Загрузить PDF

Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.^[1] С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.

1

Запишите формулу для вычисления длины. Формула: $d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}$ , где — длина отрезка, $(x_{{1}},y_{{1}})$ — координаты начальной точки отрезка, $(x_{{2}},y_{{2}})$ — координаты конечной точки отрезка.^[2]
2

Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.^[3]
3

Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты должны находится внутри первой пары скобок, а две координаты — внутри второй пары скобок.^[4]

Реклама

1

Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.^[5]
2

Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.^[6]
3

Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.
4

Вычислите длину отрезка . Для этого извлеките корень из полученной суммы чисел.

Реклама

Советы

Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.

Об этой статье

Эту страницу просматривали 24 603 раза.

Была ли эта статья полезной?

Источник

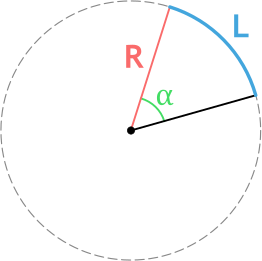
{L = dfrac{pi R alpha}{180degree}}

Длина дуги окружности — важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между радиусами и по формуле Гюйгенса. Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.

Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.

Содержание:

калькулятор длины дуги окружности
формула длины дуги окружности через радиус и угол
формула длины дуги окружности по формуле Гюйгенса
примеры задач

Если обобщить, то дуга окружности — это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:

Полная окружность — это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле L = 2πr, где r — радиус окружности.
Полуокружность — это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.
Сектор окружности — это область, ограниченная дугой окружности и двумя ее радиусами.

Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.

Формула длины дуги окружности через радиус и угол

{L = dfrac{pi R alpha}{180degree}}

R — радиус окружности

α — центральный угол (угол между радиусами) в градусах

{L = R alpha}

R — радиус окружности

α — центральный угол (угол между радиусами) в радианах

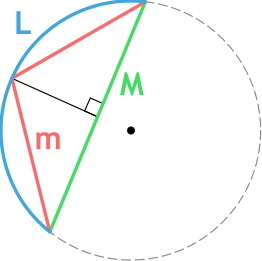
Формула длины дуги окружности по формуле Гюйгенса

{L approxeq 2m + dfrac{2m-M}{3}}

m — длина хорды m

M — длина хорды M

Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак «равно или почти равно», который записывается так — «approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.

Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.

Примеры задач на нахождение длины дуги

Задача 1

Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.

Решение

Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:

L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 6 cdot 30degree}{180degree} = dfrac{pi cdot 180degree}{180degree} = pi : см approx 3.14 : см.

Ответ: {pi : см approx 3.14 : см.}

Введем известные значения в калькулятор для проверки полученного ответа.

Задача 2

Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.

Решение

Задача аналогична предыдущей. Также воспользуемся первой формулой.

L = dfrac{pi R alpha}{180degree} = dfrac{pi cdot 3 cdot 150degree}{180degree} = dfrac{pi cdot 3 cdot 5}{6} = dfrac{pi cdot 5}{2} = dfrac{5}{2} pi : см = 2.5 pi : см approx 7.85398 : см.

Ответ: {2.5 pi : см approx 7.85398 : см.}

В проверке ответа нам снова поможет калькулятор .

Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.

Источник

Экзотические единицы длины

Следующий уникальный калькулятор служит для перевода экзотических единиц длины в…

Чей фунт тяжелее?

Следующий онлайн калькулятор о фунтах. Ранее он был очень популярен,…

Уровень жидкости в наклоненном цилиндрическом баке

Следующий онлайн калькулятор может вычислить уровень жидкости в цилиндрической таре…

Температурные шкалы

Следующий онлайн калькулятор переводит температуры между разными шкалами.
Помните калькулятор…

Старинные русские деньги

Следующий калькулятор интересен тем, что он переводит древние российские денежные…

Соответствие размеров обуви

Следующий калькулятор будет очень полезен тем, кто решил купить или…

Системы измерения плоских углов

Следующий калькулятор работает очень просто, вам нужно ввести всего одно…

Рост в русской системе мер

Следующий онлайн калькулятор считает рост человека благодаря русской системе мер…

Размер экрана

Следующий онлайн калькулятор может вычислить габариты экрана телевизоров, компьютеров, проекторов,…

Размер снимка в пикселях и формат фотографии

Перед вами 2 калькулятора: один поможет вам подобрать формат снимков…

Перевод числа плиток в единицы площади и обратно

Следующие 2 калькуляторы переводят заданное число плиток в квадратные метры…

Перевод мер площади из метрической в английскую систему и обратно

Перед вами 2 онлайн-калькулятора. Они переводят меры площади из метрической…

Перевод мер длины из русской системы в метрическую и обратно

Следующий необычный калькулятор переводит меры длины из русской системы в…

Перевод мер длины из метрической в имперскую систему и обратно

Перед вами 2 калькулятора, которые предназначены для перевода мер длины…

Перевод кельвинов в градусы цельсия

Следующий простенький калькулятор переводит введенную вами toC из кельвинов в…

Перевод из фунтов в килограммы и обратно

Следующий калькулятор предназначен для перевода кг в фунты. Также есть…

Перевод из фунтов в дюймы

Следующий онлайн калькулятор переводит калибр древних артиллерийских орудий из фунтов…

Перевод из градусов Фаренгейта в градусы Цельсия

Давайте вспомним калькулятор, который переводит градусы Цельсия в градусы Фаренгейта:…

Перевод дробных чисел из одной системы счисления в другую

Как вы уже могли заметить на нашем сайте есть несколько…

Перевод градусов Цельсия в градусы Фаренгейта

Следующий уникальный калькулятор переводит градусы Цельсия в градусы Фаренгейта. Наверное,…

Перевод градусов минут и секунд в десятичные градусы и обратно

Следующий калькулятор умеет переводить значение угла, которое задано в градусах,…

Перевод градусов в радианы

Следующий калькулятор делает перевод единиц измерения углов из градусов, минут,…

Объем сегмента цилиндра

Следующий калькулятор делает расчет объема сегмента цилиндра. Давайте посмотрим каким…

Объем жидкости в наклоненном цилиндрическом баке

Следующий онлайн-калькулятор считает объем жидкости в бочке, которая имеет цилиндрическую…

Общее время наработки аппарата

Следующий калькулятор служит для детального подсчета суммарной работы аппарата.
Вам…

Сочетание цветов

Перед вами отличный помощник для IT специалистов. С помощью данного…

О римских цифрах

Следующий калькулятор переводит числа, записанные римскими цифрами в простые десятичные…

Метров в секунду и километров в час

Следующий калькулятор переводит скорость из м/с в км/час. Часто при…

Конвертер единиц давления

Начнем с истории. В 17 веке итальянским ученым Торричелли было…

Калькулятор горловины для цилиндрического бака

Следующий онлайн-калькулятор рассчитывает параметры горловины для цилиндрического бочки.
Все работает…

Источник