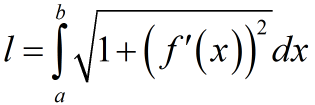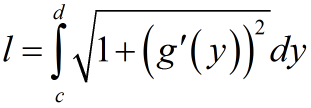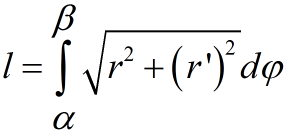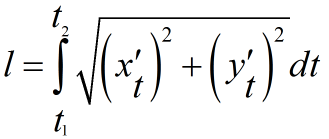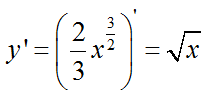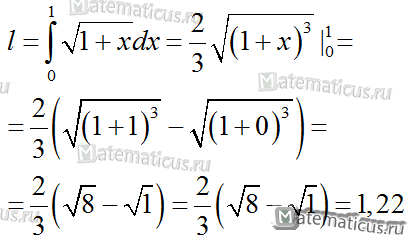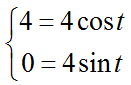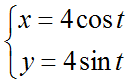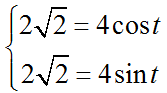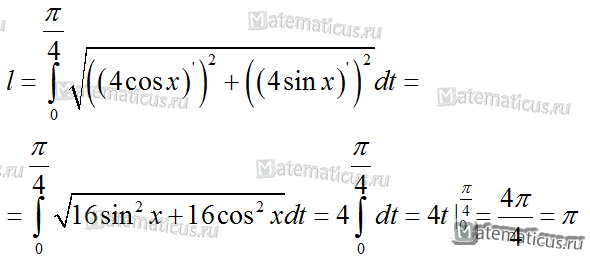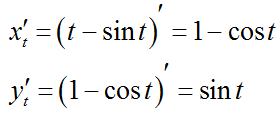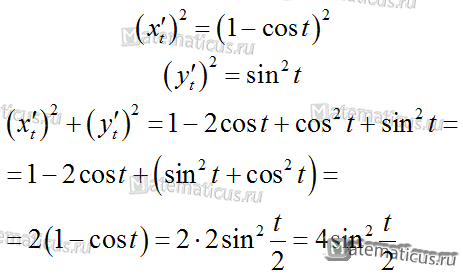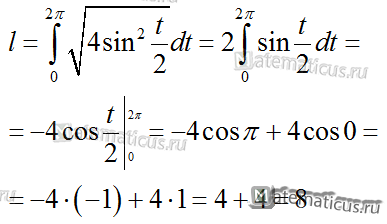Отсюда находим S
= 3S1=
.
Линия (L)
в пространстве называется гладкой, если
в каждой точке (L)
можно провести касательную к этой линии.
Если линия без самопересечений задана
параметрическими уравнениями
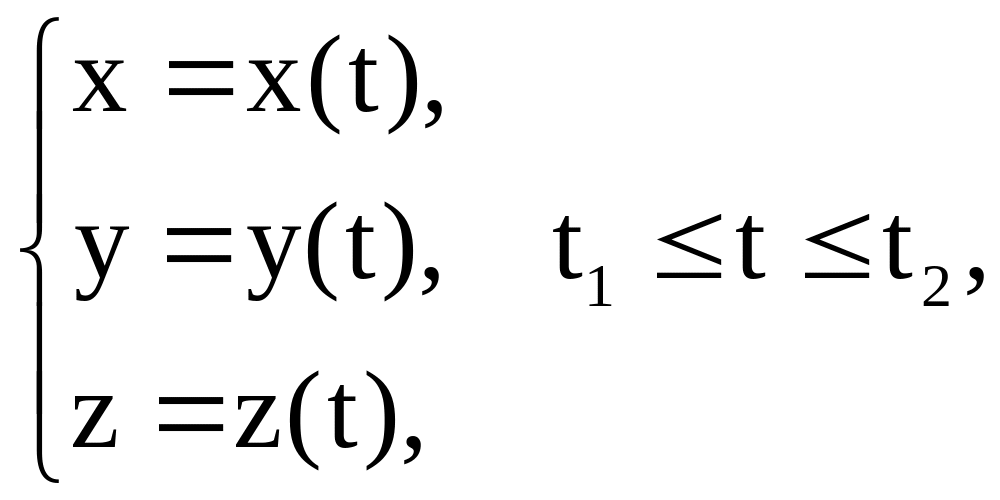
то
дифференцируемость x(t),
y(t),
z(t)
гарантирует гладкость линии; аналогичное
утверждение справедливо для плоской
линии. Если линия без самопересечений
на плоскости с заданной полярной системой
координат определена полярным уравнением
,
то и в этом случае дифференцируемость
влечёт гладкость этой линии.
Если гладкая линия
(L) на плоскости (в пространстве) задана
параметрическими уравнениями
,
(и вдобавок к этому
для линии в пространстве),
,
то длина
линии (L) находится по формуле
(
).
Если гладкая линия
(L) задана явным уравнением
,
,
то
.
Для гладкой линии
(L), заданной полярными уравнениями,
,
.
Пример 26.
Найти длину
линии, заданной уравнением
,
,
.
Решение.
Имеем
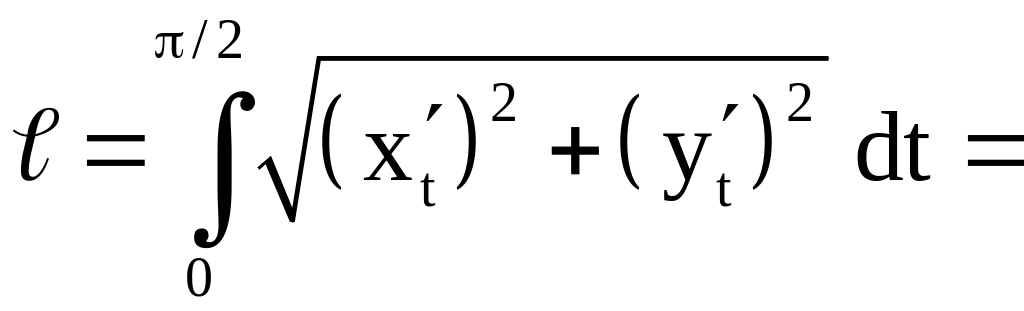
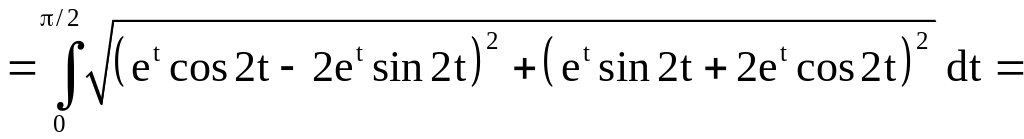
.
Пример 27.
Найти длину дуги логарифмической
спирали
,
находящейся внутри окружности
.
Решение. Дуге
спирали, лежащей внутри окружности
,
соответствуют значения
.
Поэтому
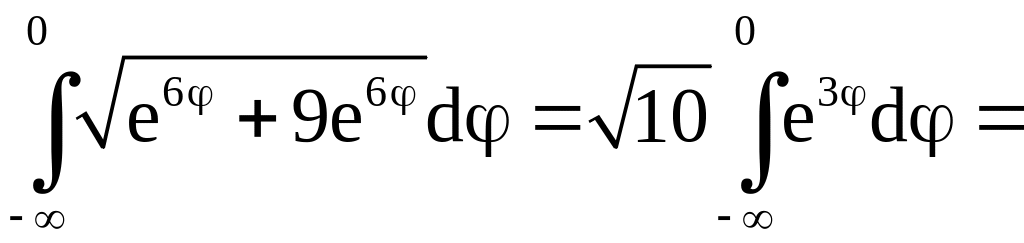
.
13. Вычисление объёмов тел
Если в пространстве
заданы ось 0х, тело (Т), проекцией которого
на 0х является отрезок [a; b] , и для любого
x
[a; b] известна площадь S(x) поперечного
сечения S(x), то объём V тела (Т) находится
по формуле
.
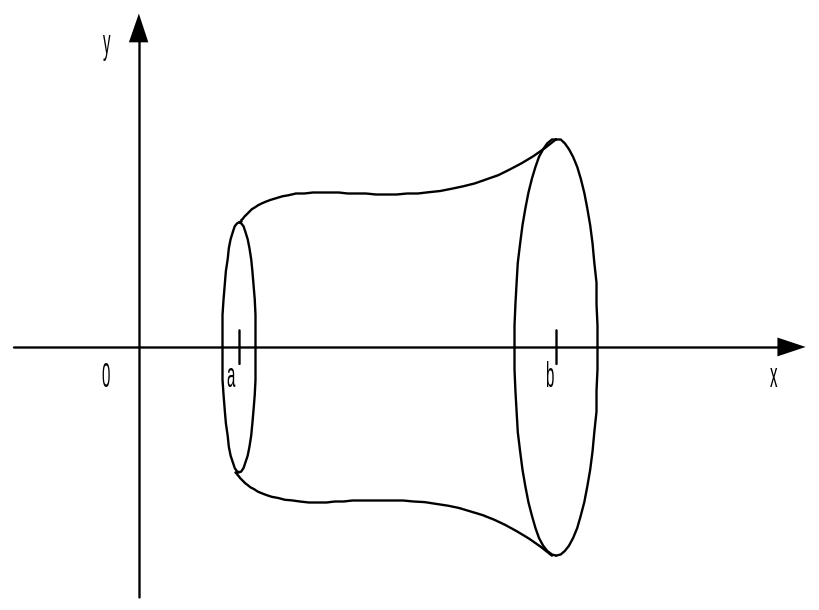
В
частности, если тело (Т) получено путём
вращения графика функции
,
вокруг оси 0х, то объём тела вращения
равен
.
При вращении
графика функции f(x) вокруг оси 0у формула
объёма принимает вид
.
Пример 28. Найти
объём V тела (Т), ограниченного эллипсоидом
.
Решение.
Проекцией тела (Т) на ось 0х является
отрезок [–a; a]. Найдём формулу площади
S(x) поперечного сечения,
x
[a; b]. Перепишем
уравнение эллипсоида в виде
.
Это есть уравнение
поперечного сечения эллипсоида
плоскостью, проходящей через точку x и
перпендикулярной оси 0х. А мы уже знаем
(задача 22), что площадь фигуры, заключённой
внутри этого эллипса, равна
.
Следовательно,
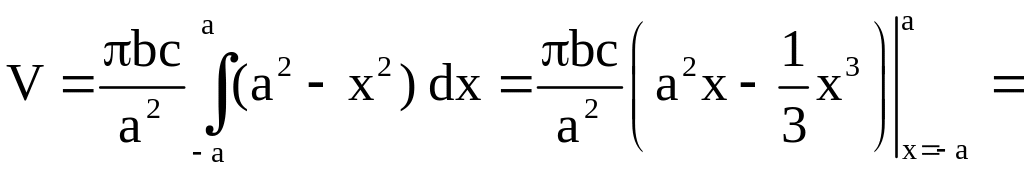
.
14. Приближённое вычисление определённых интегралов
Формула
Ньютона–Лейбница является хорошим
средством для вычисления определённого
интеграла. Однако возможности применения
этой формулы сильно ограничены тем, что
далеко не для всякой элементарной
функции первообразная к ней является
элементарной функцией. Другими словами,
если f(x) является элементарной функцией,
то
могут оказаться неэлементарными
функциями (более того, если f(x) образовать
наобум как суперпозицию элементарных
функций, то, скорее всего,
будут неэлементарными функциями). В
таком случае говорят, что
является неберущимся интегралом.
Приведём несколько таких примеров:
,
,
,
.
Дело обстоит так, что в большинстве
случаев решение прикладных задач требует
вычисления определённых интегралов от
функций, первообразные которых выходят
за рамки класса элементарных функций,
что делает невозможным применение
формулы Ньютона–Лейбница. В таких
случаях довольствуются приближённым
вычислением определённого интеграла,
или, как говорят, применяют методы
численного интегрирования. К простейшим
методам численного интегрирования
относятся методы прямоугольников,
трапеций и парабол (Симпсона).
Разобьём отрезок
[a;b] на n равных частей точками
;
называется шагом разбиения.
Обозначим
,
,
.
По методу
прямоугольников
;
;
.
Все эти три формулы
называются формулами прямоугольников.
Метод трапеций
состоит в применении формулы (при тех
же обозначениях)
.
В методе парабол
(Симпсона) отрезок [a; b] разбивается на
чётное число 2n отрезков равной длины
точками a1
= x0
< x1
< x2
< …< x2n
= b. Согласно формуле Симпсона (при тех
же обозначениях)
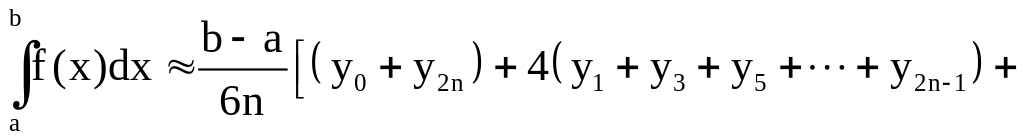
.
Точность вычисления
растёт с ростом n. Погрешность Rn[f]
приведённых выше формул оценивается
величинами:
для формулы
прямоугольников
,
для формулы трапеций
,
для формулы Симпсона
,
где
,
.
Пример 29. Вычислите
приближённо
методами:
а) прямоугольников,
б) трапеций, в) Симпсона, взяв
.
В методах прямоугольников и трапеций
оценить погрешность вычисления.
Решение.
а) Составим таблицу
.
|
xк |
2 |
2,2 |
2,4 |
2,6 |
2,8 |
|
yк |
0,8326 |
0,8880 |
0,9357 |
0,9775 |
1,0147 |
|
xк |
3 |
3,2 |
3,4 |
3,6 |
3,8 |
|
yк |
1,0481 |
1,0785 |
1,1062 |
1,1318 |
1,1554 |
Воспользуемся
первой из формул прямоугольников
0,2(0,8326
+ 0,8880 + 0,9357 + 0,9775 + 1,0147 + 1,0481 + + 1,0785 + 1,1062
+ 1,1318 + 1,1554) = 0,210,1685
= 2,0337.
Оценим погрешность
.
Нетрудно видеть, что
.
Отсюда
и погрешность не превышает
.
б) Для применения
формулы трапеций дополним выше
составленную таблицу ещё одним значением:
.
Имеем
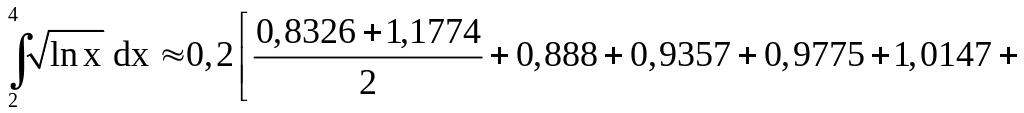
.
Погрешность
вычисления равна
.
в) Рассмотрим нашу
таблицу (h
= 0,1).
|
xк |
2 |
2,1 |
2,2 |
2,3 |
2,4 |
|
yк |
0,832555 |
0,861358 |
0,887951 |
0,912639 |
0,935665 |
|
xк |
2,5 |
2,6 |
2,7 |
2,8 |
2,9 |
|
yк |
0,957231 |
0,977503 |
0,996620 |
1,014702 |
1,031848 |
|
xк |
3 |
3,1 |
3,2 |
3,3 |
3,4 |
|
yк |
1,048147 |
1,063674 |
1,078495 |
1,092668 |
1,106244 |
|
xк |
3,5 |
3,6 |
3,7 |
3,8 |
3,9 |
|
yк |
1,119269 |
1,131784 |
1,143824 |
1,1554224 |
1,166609 |
|
xк |
4 |
||||
|
yк |
1,177410 |
Отсюда находим
[(0,832555
+ 1,17741) + 4(0,861358 + 0,912639 +
+0,957231 + 0,99662 + 1,031848
+ 1,063674 + 1,092668 + 1,119269 + +1,143824 + 1,166609) + 2(0,887951
+ 0,935665 + 0,977503 + 1,014702 + +1,048147 +1,078495 +1,106244 +
1,131784 +1,155422)] =
62,064751
2,068825
2,0688.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При вычислении любой длины следует помнить, что это величина конечная, то есть просто число. Если имеется в виду длина дуги кривой, то такая задача решается с помощью определенного интеграла (в плоском случае) или криволинейного интеграла первого рода (по длине дуги). Дуга АВ будет обозначаться UАВ.
Первый случай (плоский). Пусть UАВ задана плоской кривой y = f(x). Аргумент функции изменятся в пределах от а до b и она непрерывно дифференцируема этом отрезке. Найдем длину L дуги UАВ (см. рис. 1а). Для решения этой задачи разбейте рассматриваемый отрезок на элементарные отрезки ∆xi, i=1,2,…,n. В результате UАВ разобьется на элементарные дуги ∆Ui, участков графика функции y=f(x) на каждом из элементарных отрезков. Найдете длину ∆Li элементарной дуги приближенно, заменив ее соответствующей хордой. При этом можно приращения заменить дифференциалами и использовать теорему Пифагора. После вынесения из квадратного корня дифференциала dx получите результат, приведенный на рисунке 1b.
Как вычислить длину кривой
Второй случай (дуга UАВ задана параметрически). x=x(t), y=y(t), tє[α,β]. Функции x(t) и y(t) имеют непрерывные производные на отрезке этом отрезке. Найдите их дифференциалы. dx=f’(t)dt, dy=f’(t)dt. Подставьте эти дифференциалы в формулу для вычисления длины дуги в первом случае. Вынесите dt из квадратного корня под интегралом, положите х(α)=а, x(β)=b и придете к формуле для вычисления длины дуги в данном случае (см. рис. 2а).
Третий случай. Дуга UАВ графика функции задана в полярных координатах ρ=ρ(φ) Полярный угол φ при прохождении дуги изменяется от α до β. Функция ρ(φ)) имеет непрерывную производную на отрезке ее рассмотрения. В такой ситуации проще всего использовать данные, полученные на предыдущем шаге. Выберите φ в качестве параметра и подставьте в уравнения связи полярных и декартовых координат x=ρcosφ y=ρsinφ. Продифференцируйте эти формулы и подставьте квадраты производных в выражение на рис. 2а. После небольших тождественных преобразований, основанных в основном, на применении тригонометрического тождества (cosφ)^2+(sinφ)^2=1, получите формулу для вычисления длины дуги в полярных координатах (см. рис.2b).
Четвертый случай (пространственная кривая, заданная параметрически). x=x(t), y=y(t), z=z(t) tє[α,β]. Строго говоря, здесь следует применить криволинейный интеграл первого рода (по длине дуги). Криволинейные интегралы вычисляют переводом их в обычные определенные. В результате ответ останется практическим таким же как и случае два, с тем лишь отличием, что под корнем появится добавочное слагаемое – квадрат производной z’(t) (см рис. 2с).
Примеры:
Пример 1. Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у’ = ƒ'(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную
Применим схему I (метод сумм).
1. Точками х0 = а, х1…, хn = b (х0 < x1 < …< хn) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М0 = А, M1,…,Mn =В на кривой АВ. Проведем хорды М0M1, M1M2,…, Мn-1Мn, длины которых обозначим соответственно через ΔL1, AL2,…, ΔLn. Получим ломаную M0M1M2 … Mn-ιMn, длина которой равна Ln=ΔL1 + ΔL2+…+ ΔLn =
2. Длину хорды (или звена ломаной) ΔL1 можно найти по теореме Пифагора из треугольника с катетами Δxi и Δуi:
По теореме Лагранжа о конечном приращении функции Δуi=ƒ'(сi)•Δхi, где ci є (xi-1;xi). Поэтому
а длина всей ломаной M0M1… Мn равна
3.Длина l кривой АВ, по определению, равна
.
Заметим, что при ΔLi→0 также и Δxi →0 ΔLi =и, следовательно, |Δxi|<ΔLi).
Функция непрерывна на отрезке [а; b], так как, по условию, непрерывна функция ƒ'(х). Следовательно, существует предел интегральной суммы (41.4), когда max Δxi→ 0:
Таким образом,или в сокращенной записи l =
Если уравнение кривой АВ задано в параметрической форме
где x(t) и y(t) — непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле
Формула (41.5) может быть получена из формулы (41.3) подстановкой x = x(t),dx = x'(t)dt,
Пример 2. Определить длину окружности x2 + y2 = r2. Решение. Вычислим сначала длину четвертой части окружности, лежащей в первом квадранте. Тогда уравнение дуги AB будет, откуда
,следовательно,
Длина всей окружности L = 2πr.
Пример 3. Найти длину дуги кривой y2 = x3 от x = 0 до x = 1 (y > 0). Решение. Дифференцируя уравнение кривой, найдем y’ = (3/2)x1/2, откуда
Пример 4. Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x).
Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимируовать прямолинейным участком (см. рисунок 1).
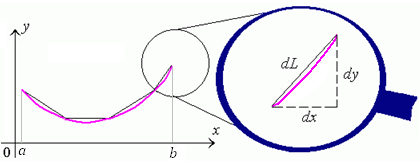
Рис. 1. Аппроксимация элемента дуги кривой прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
 |
(1) |
где y ‘ – производная функции y = f(x) по переменной x.
Длина дуги равна сумме длин составляющих ее элементов:
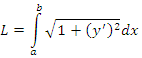 . . |
Пример 5.
Калькулятор длины дуги кривой линии в декартовых координатах
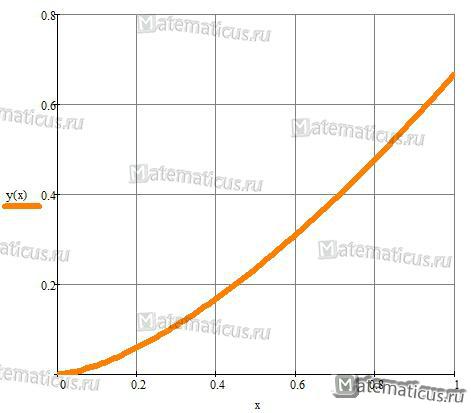
Одним из приложений определенного интеграла является вычисление длины дуги плоской кривой. На рисунке изображен график функции :
Для того, чтобы узнать длину дуги кривой линии изображенной на рисунке, необходимо вычислить определенный интеграл:
В более общем случае, если у нас задана функция в декартовых координатах и стоит задача найти длину дуги этой кривой между точками и , нам необходимо вычислить интеграл:
В приведенной выше формуле, выражение означает, что сначала нужно вычислить производную функции , а затем полученное выражение возвести в квадрат.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, позволяет вычислить длину кривой, заданной в декартовых координатах для любой, даже очень сложной функции.
Как найти длину дуги кривой с помощью интеграла
Задачи на вычисление длины дуги кривой — однотипные. Существуют чёткие схемы для решения таких задач по формулам, которые отличаются в зависимости от того, какими и сколькими уравнениями задана кривая. Формулы представляют собой интегралы от корня, под которым в тех или иных сочетаниях присутствуют производные функций, которыми задана кривая. Следовательно, для того, чтобы вычислять длину дуги кривой, требуется уметь вычислять производные и интегралы. При вычислении интегралов возможны типичные трудности, связанные, например, с выбором подходящей подстановки. Эти задачи будем решать в примерах к данному уроку.
Вычисление длины дуги кривой, заданной в прямоугольных координатах
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.
Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).
Возьмём на дуге AB точки A, M 1 , M 2 , . M i , . B с абсциссами x 0 = a, x 1 , x 2 , . x i , . b = x n и проведём хорды AM 1 , M 1 M 2 , . M n-1 B , длины которых обозначим соответственно через Δs 1 , Δs 2 , . Δs n . Тогда получим ломаную AM 1 M 2 . M n-1 B , вписанную в дугу AB. Длина ломаной равна

Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

Этот предел интегральной суммы равен определённому интегралу

Формула выше и есть формула для вычисления дуги кривой.
Пример 1. Найти длину дуги кривой 

Решение. Находим производную данной функции:
Используем формулу (1), подставляя найденную производную:
Ответ: длина дуги кривой равна 74.
Пример 2. Найти длину окружности 
Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

откуда находим производную функции:
Используем формулу (1) подставляя в неё производную, получаем:
Ответ: длина всей окружности равна 
Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

Вычисление длины дуги кривой, заданной параметрически
Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:
В этом случае длину дуги кривой следует находить по формуле

Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями
если 
Решение. Рассчитаем интервал, в котором будет меняться значение t, если 
Вычислим производные функций x и y:
Используем формулу (3):

Ответ: длина дуги кривой равна 26.
Если параметрическими уравнениями
задана пространственная кривая, то длина её дуги вычисляется по формуле:

Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями
Решение. Вычислим производные функций x, y и z:
Используем формулу (4):
Вычисление длины дуги кривой, заданной в полярных координатах
Пусть кривая задана в полярных координатах:
Длина её дуги вычисляется по формуле:

Пример 5. Найти длину дуги кривой, заданной в полярных координатах 
Решение. Вычислим производную функции:

Заданная кривая — кардиоида (рисунок выше). Так как она симметрична, вычислим только ту часть длины дуги, у которой 

Вычисление длины дуги
Формула для вычисления длины дуги кривой заданной уравнением у=f(x) в прямоугольной системе координат:
a — начала дуги по оси OX;
b — конец дуги по оси OX a
Если плоская кривая задана уравнением x=g(y) то формула имеет вид:
c — начала дуги по оси OY;
d — конец дуги по оси OY a
Если кривая задана в полярных координатах r=r(φ), α≤φ≤β, то длина дуги вычисляется по формуле:
Если кривая задана параметрическим уравнением вида x=x(t) и y=y(t), то длина дуги определяется по формуле
t2, t1 — значения параметров, которые соответствуют концам дуги t1
Найти длину дуги функции на промежутке от 0 до 1.
Найдем производную функции:
Возведём в квадрат функцию:
Подставляя в формулу, найдем длину дуги:
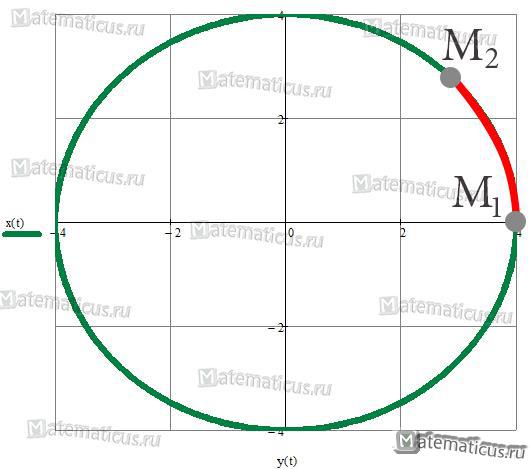
Найти длину дуги окружности от точки $left( <4;0>right)$ до точки $left( <2sqrt 2 ;2sqrt 2 >right)$. Уравнение окружности задано в параметрическом виде.
Найдем параметр t в точках M1 и M2, решим системы уравнений.
Здесь t1=0
Подставляя в формулу, найдем длину дуги окружности.
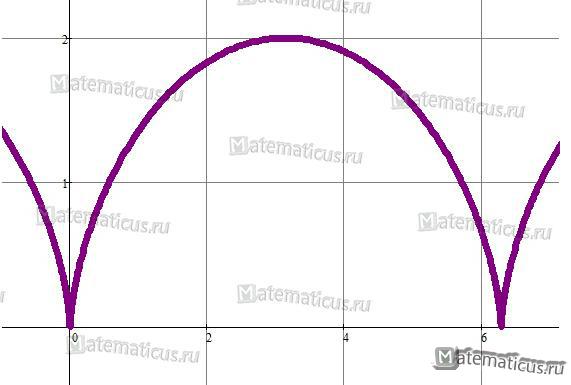
Вычислить длину дуги одного лепестка циклоиды. Уравнение циклоиды задано параметрическим уравнением.
Продифференцируем по t параметрические уравнения циклоиды:
Подставляя в формулу, получаем
One comment
Была бы оценка 5, если бы не дурак, который не от большого ума изукрасил весь текст, особенно формулы и ответы, серыми узорами! Сколько времени и усилий ушло на расшифровку ответов! Так что 3,5 балла — это ещё слишком много! Так и передайте идеологу этой мазни!
источники:
http://function-x.ru/integral502.html
http://www.matematicus.ru/vysshaya-matematika/integralnoe-ischislenie/vychislenie-dliny-dugi
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
длина:дуги:x,:0,:1
-
длина:дуги:sqrt{1-x^{2}}
-
длина:дуги:ln(sec(x)),:[0,:frac{pi}{4}]
-
длина:дуги:y=2x^{2}+3,:0le xle 1
- Показать больше
Описание
Найдите длину дуги функций между интервалами шаг за шагом
arc-length-calculator
длина дуги y=2x^{2}+3, 0le xle 1
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice Makes Perfect
Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…
Read More
Введите Задачу
Сохранить в блокнот!
Войти

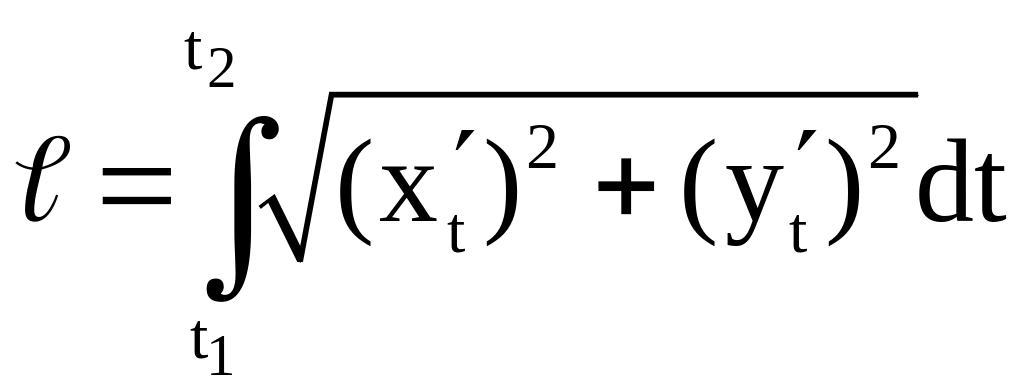
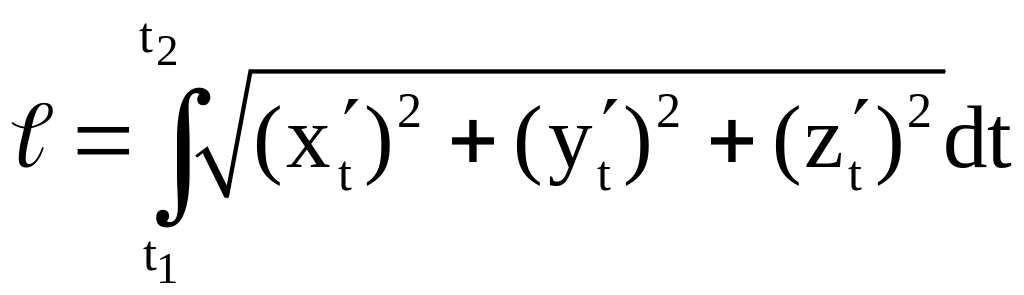
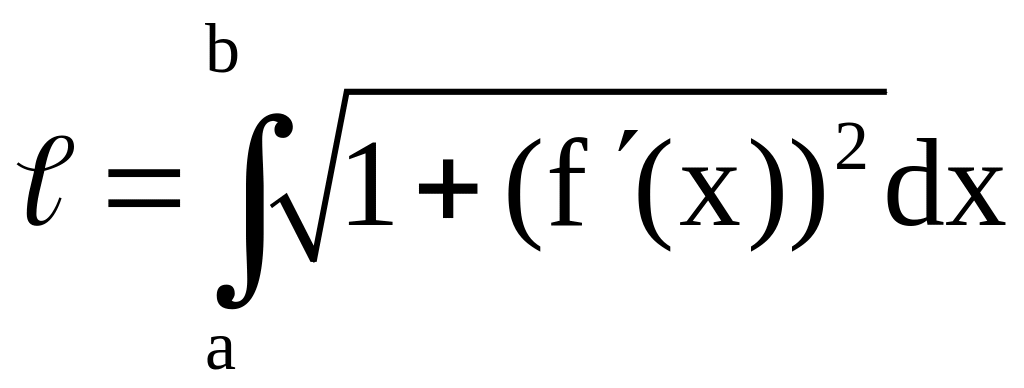

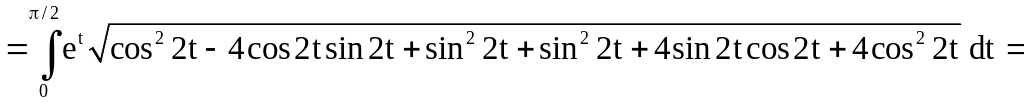
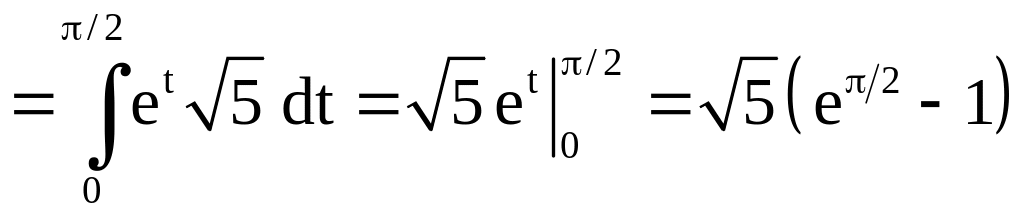
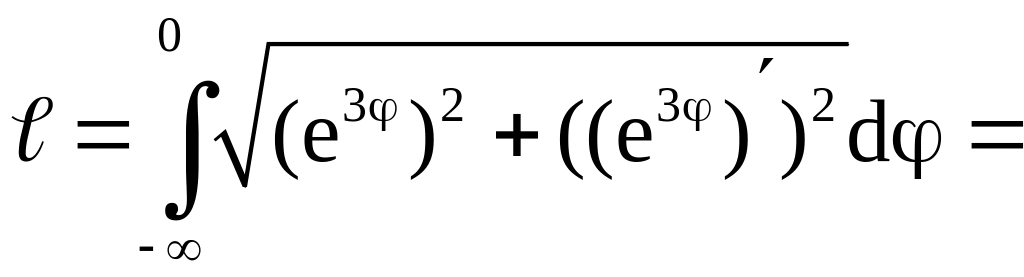
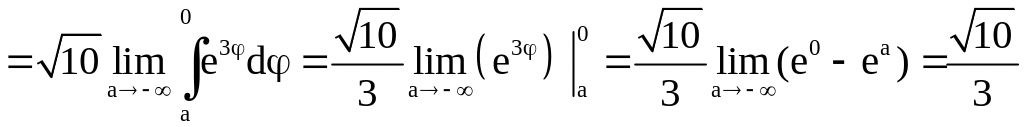
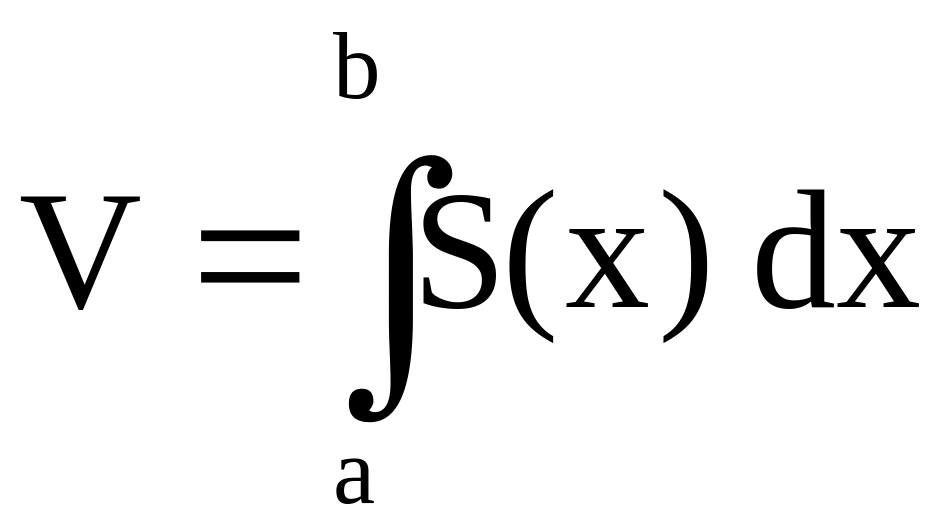
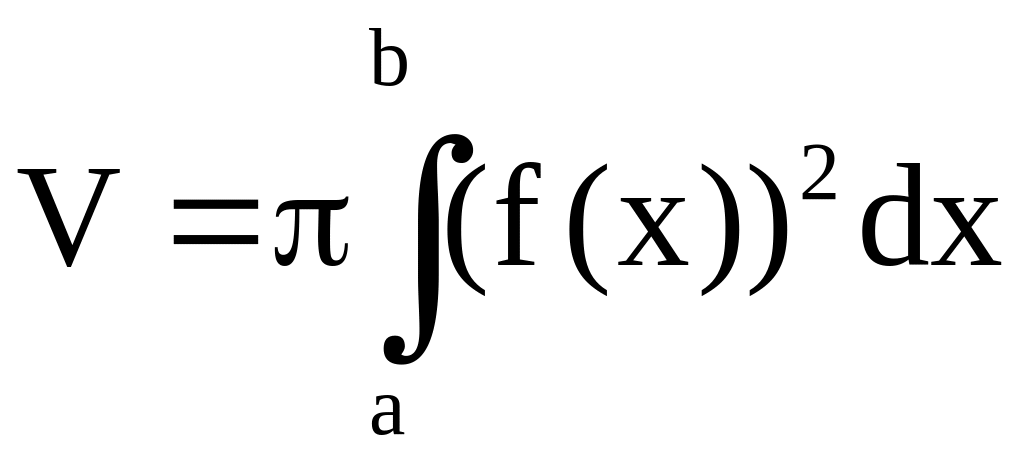
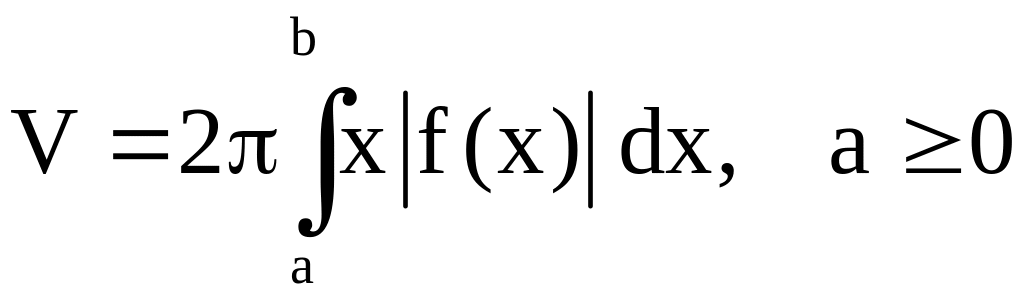

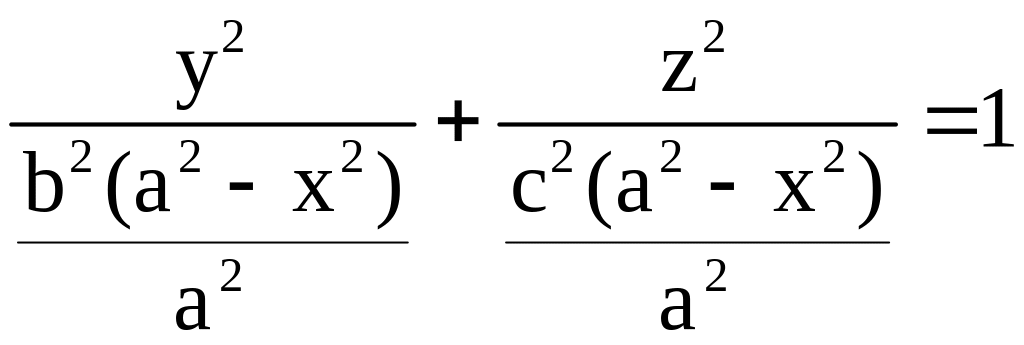
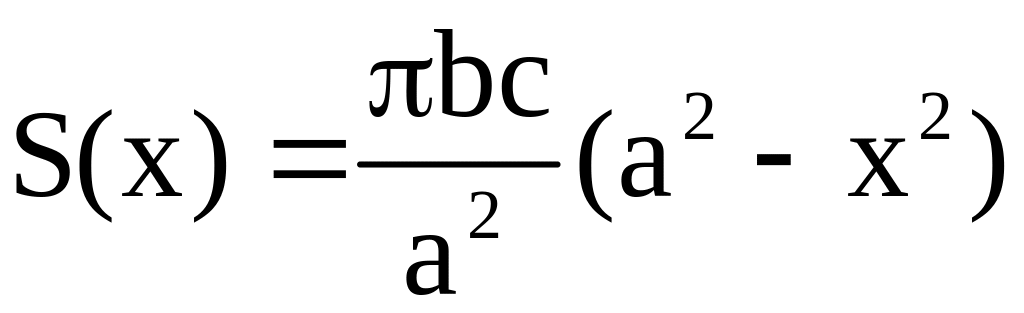
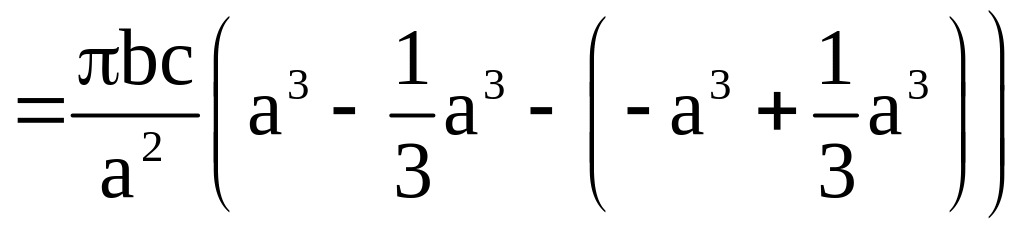
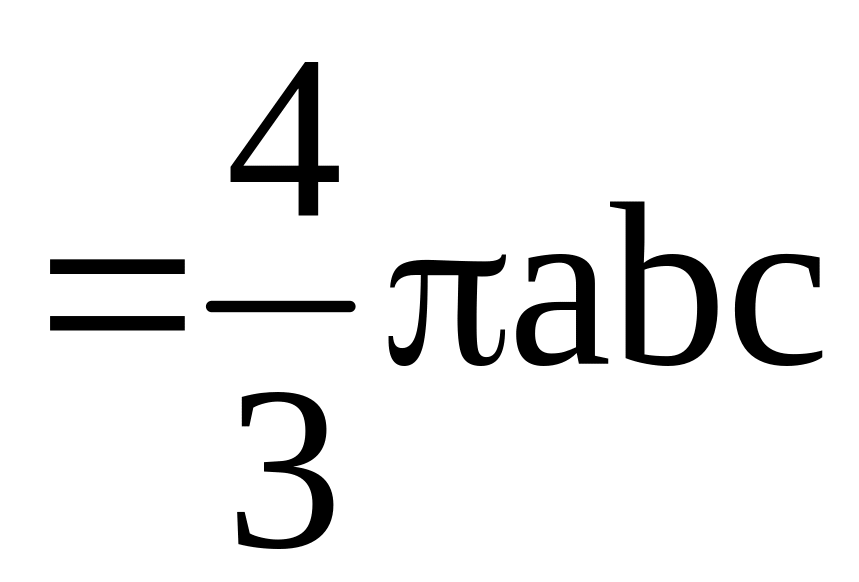
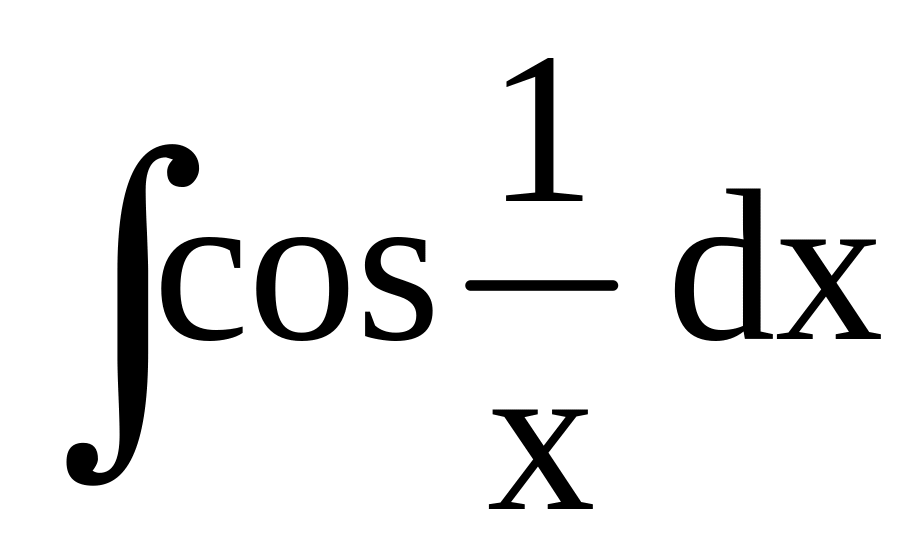
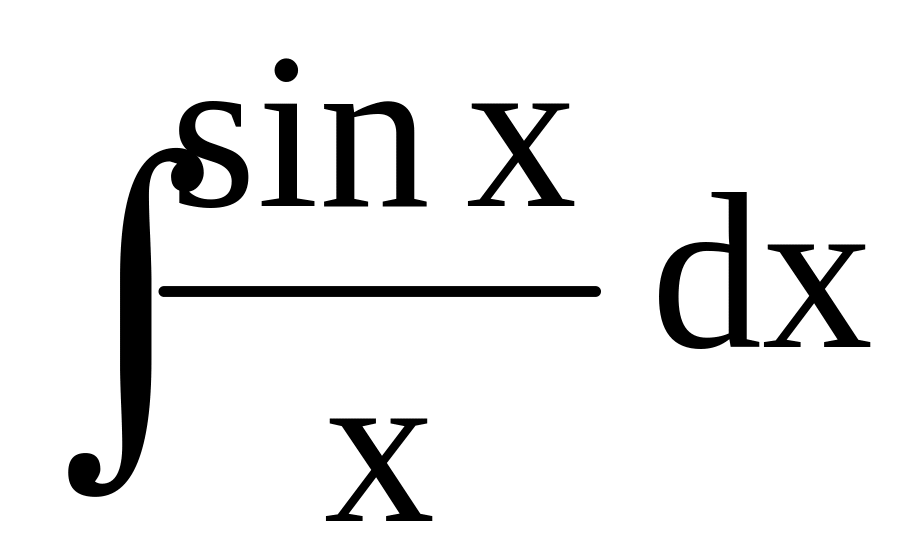
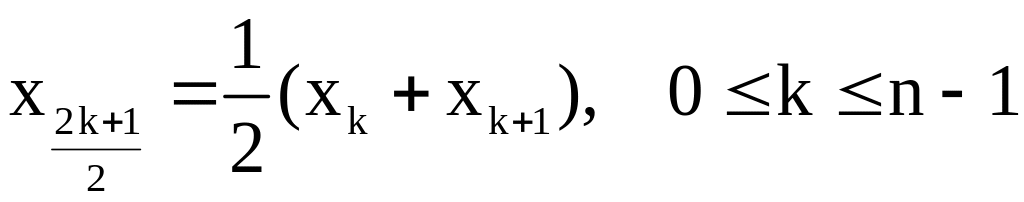
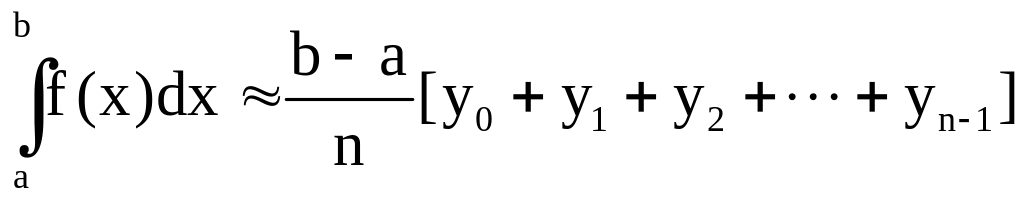
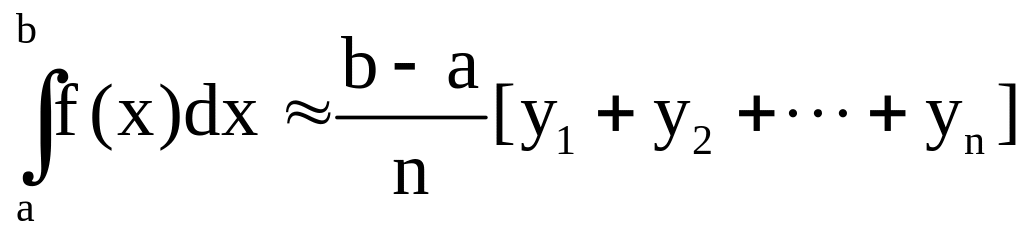
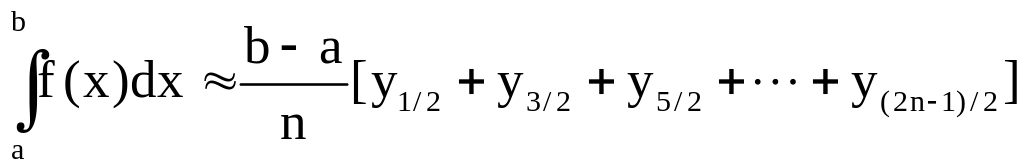
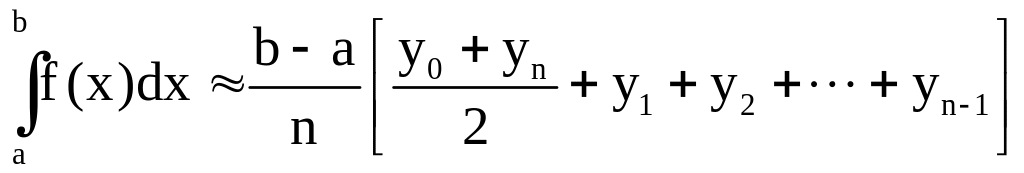
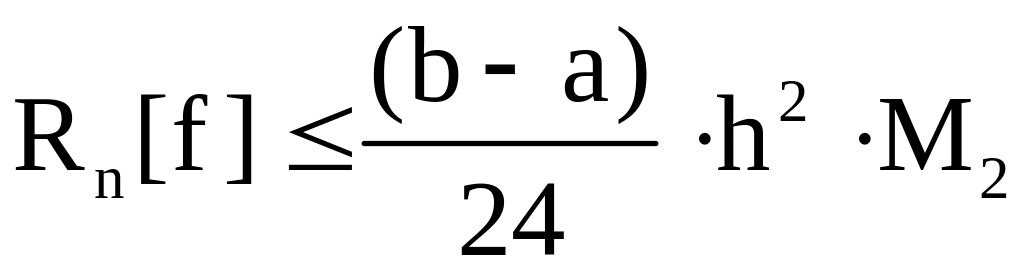
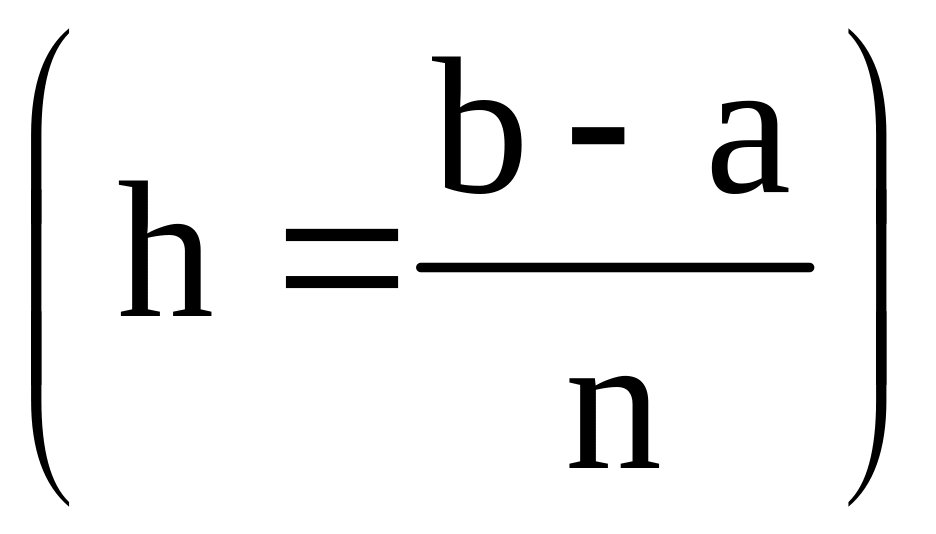
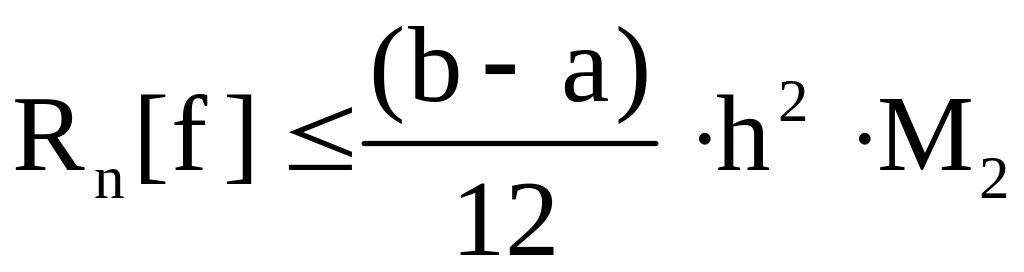
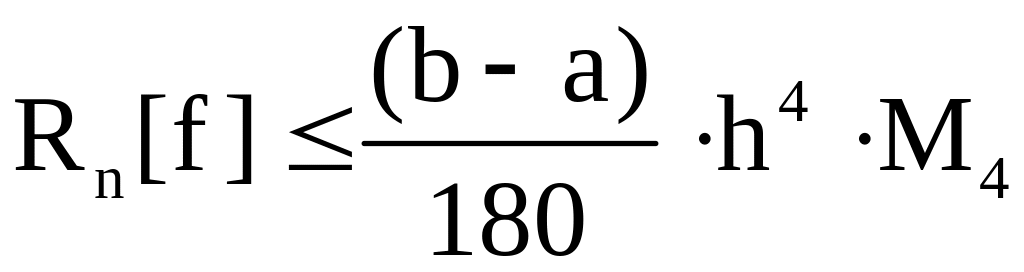
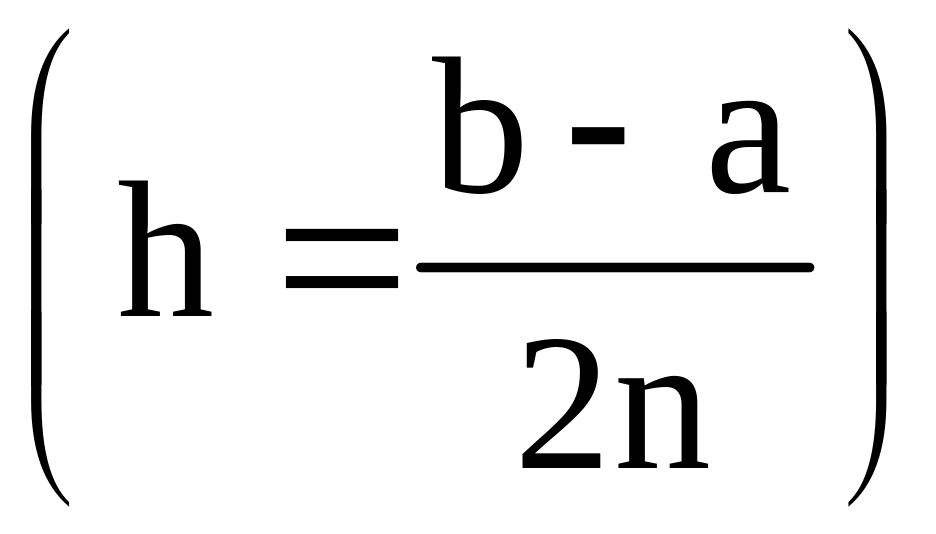
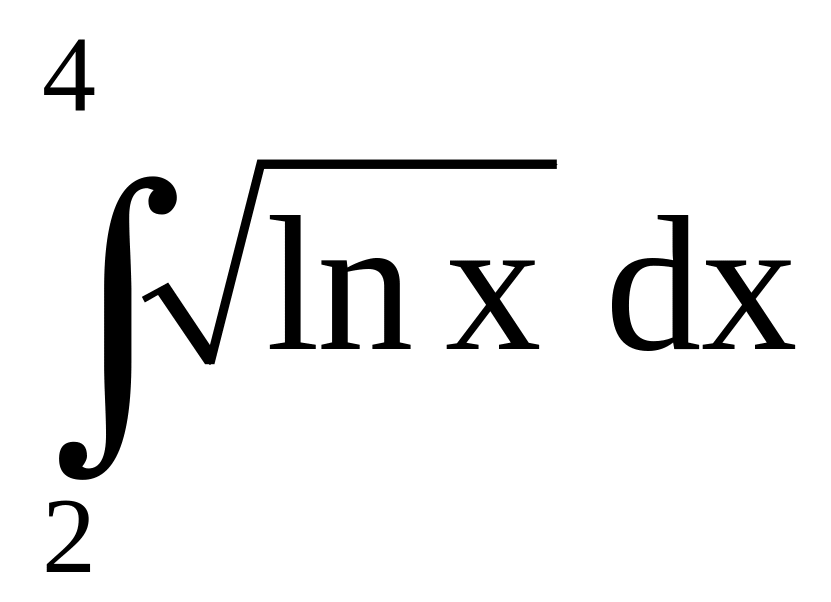

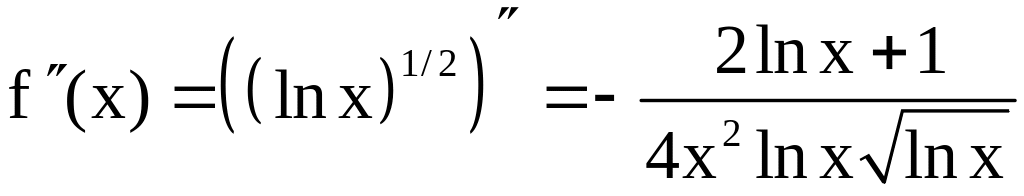
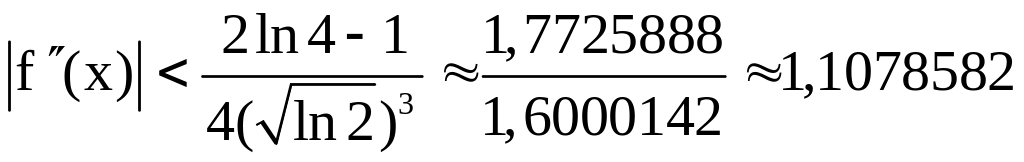
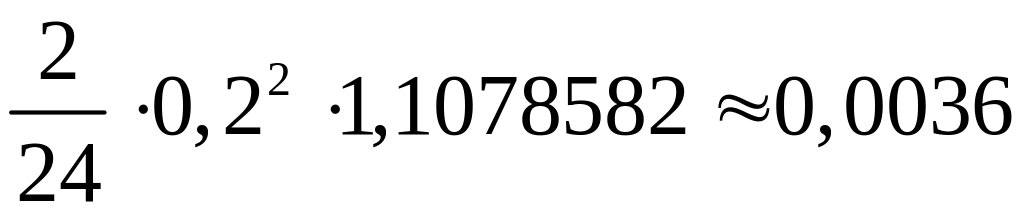
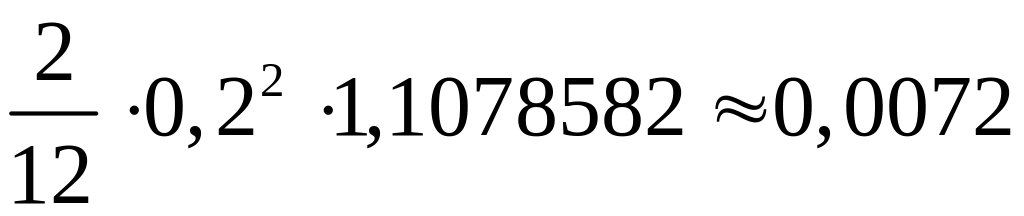
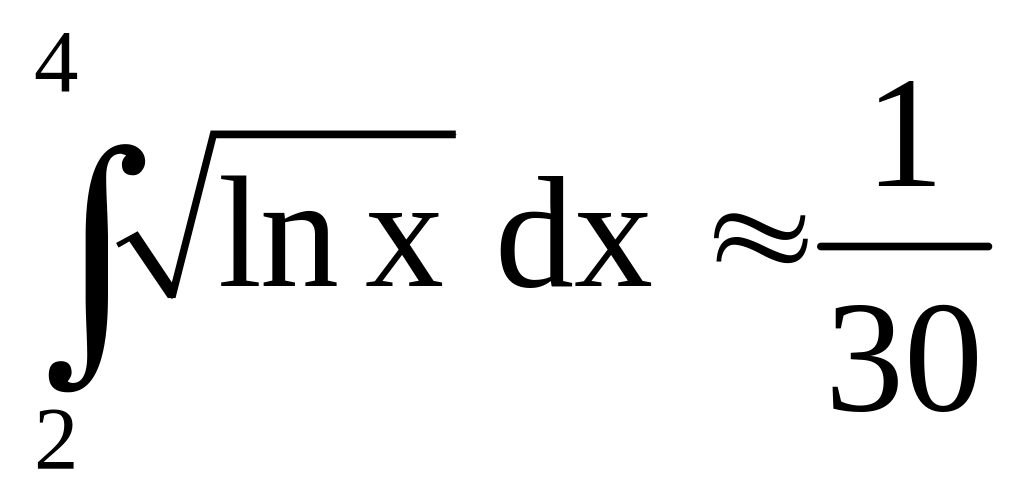
![1_5254fef39271a5254fef392758[1] 1_5254fef39271a5254fef392758[1]](https://ic.pics.livejournal.com/wrtorr/66163308/11897/11897_900.png)