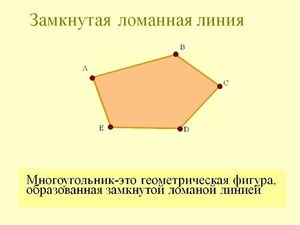
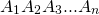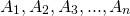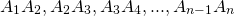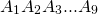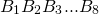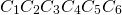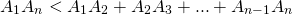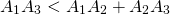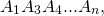Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA .
Замкнутая и незамкнутая ломаная
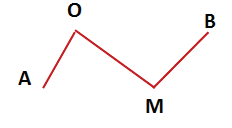
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
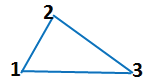
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
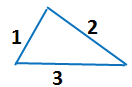
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ломаная линия
Ломаная линия состоит из отрезков — звеньев.
Конец одного отрезка — начало другого. Никакие два соседние звена не лежат на одной прямой.
Концы каждого звена — это вершины. Их можно обозначать буквами.
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
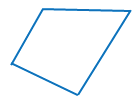
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Считается ли треугольник ломаной
- Что такое ломаная
- Что такое многоугольник
- Что такое прямоугольник
Ломаная линия состоит из вершин и отрезков, соединяющих эти вершины. При этом основное требование – любые два последовательных отрезка не лежат на одной прямой.
Составные отрезки ломаной называются ее сторонами или звеньями, а их концы – вершинами ломаной. Наименьшее возможное количество звеньев ломаной – два. Конечные вершины ломаной называются черными точками.
Графически линию обозначают по названиям ее вершин, например, ломаная ABCDEFG. Ломаная линия может быть замкнутой, т.е. ее конечные вершины совпадают. Разновидностями такой линии являются многоугольники. Многоугольник – это плоская замкнутая ломаная, которая не имеет самопересечений. Вершины ломаной называются вершинами многоугольника, а ее звенья – сторонами многоугольника.
Многоугольник с тремя сторонами и вершинами называется треугольником. Замкнутая ломаная с четырьмя сторонами может быть квадратом, прямоугольником, ромбом, параллелограммом, трапецией. Фигура с пятью и более сторонами называется n-угольником, где n – число вершин.
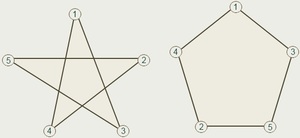
Ломаная линия может иметь самопересечения. Классическим примером замкнутой ломаной с самопересечениями является пятиконечная звезда.
Разновидностью ломаной линии является зигзаг, в котором отрезки параллельны друг другу через один, а последовательные образуют одинаковый угол. Зигзаги используются в швейном деле, а также при декоративном оформлении предметов обихода (посуды, мебели, книг) в качестве орнамента.
Ломаная линия имеет широкое применение в картографии (построение маршрутов и схематичное изображение улиц), архитектуре (линии зданий и домой), ландшафтном дизайне (расположение дорожек, декоративное оформление), химии (молекулярные структуры и соединения), медицине (медицинские мониторы для наблюдения за сердечным ритмом) и в других областях.
Ломаная
— это фигура, состоящая из точек
и последовательно соединяющих эти точки отрезков.
— вершины ломаной, отрезки
Ломаная называется простой, если она не имеет самопересечений.
не является простой (это ломаная с самопересечением).
Ломаная, начало которой совпадает с её концом, называется замкнутой.
Длиной ломаной называется сумма длин всех её звеньев.
Длина ломаной не меньше длины отрезка, соединяющего её концы.
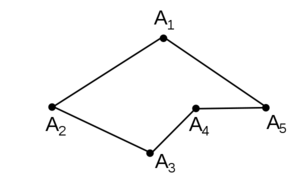
Дано :
Проведём отрезок A1A2.
в которой два звена A1A2 и A2A3 заменили одним звеном A1A3 имеет длину, не большую длины исходной ломаной.
Аналогично в новой ломаной заменим звенья A1A3 и A3A4 на A1A4. Эта новая ломаная также имеет длину, не большую длины исходной ломаной.
На последнем шаге мы придём к отрезку A1An который также имеет длину, не большую длины исходной ломаной, то есть
Ломаной линией в геометрии принято называть геометрическую фигуру, которая состоит из двух или нескольких отрезков. Конец одного отрезка является началом другого. Обязательное условие, которому подчиняется любая ломаная, — соседние отрезки не должны располагаться на одной прямой.
Эти геометрические фигуры находят самое широкое применение в разных областях науки и практики:
- Картография — для построения изображений улиц и схем маршрутов.
- Архитектура — очертания зданий и строений.
- Ландшафтный дизайн — декоративное оформление и расположение тропинок.
- Химия — молекулярная структура сложных полимерных соединений.
- Медицина — мониторы для контроля функционального состояния органов и систем.
Типы ломаных линий
Рассматриваемые геометрические фигуры могут быть выстроены самыми разнообразными способами — они могут быть незамкнутыми и замкнутыми, пересекающимися и непересекающимися.
Замкнутая ломаная соответствует определенной геометрической фигуре — многоугольнику.
Если отрезки одной такой фигуры имеют точки пересечения друг с другом — эта линия называется самопересекающейся.
Всего существует 4 типа подобных линий по своей структуре:
- Замкнутые, которые не имеют пересечений.
- Незамкнутые, которые не имеют пересечений.
- Незамкнутые самопересекающиеся.
- Замкнутые, имеющие самопересечения.
Разновидностью такой геометрической фигуры может считаться зигзаг, у которого последовательные отрезки образуют прямой угол и параллельны друг другу через один. Зигзагами широко пользуются в обиходе — в портновском мастерстве, декоративном искусстве, оформлении предметов обихода.
Особенности замкнутых линий
Рассмотрим подробнее составляющие части этой геометрической фигуры.
- Один отрезок из тех, что составляют описываемую фигуру, называется ее звеном. Ломаной может считаться такая линия, которую составляют как минимум два отрезка — звена. Если звено одно — это просто единичный отрезок.
- Существует также понятие вершины ломаной. Этим термином принято называть точку, в которой соединяются концы двух звеньев. Такие точки в геометрии принято обозначать с помощью заглавных латинских букв. Сама ломаная называется сочетанием обозначений этих вершин. Например, названием такой линии может послужить сочетание ABCDEF.
- Если концы крайних звеньев этого геометрического объекта соединяются в одной точке, такая линия называется замкнутой.
- Ломаная линия может пересекать саму себя.
- Конечные вершины такой фигуры в геометрии принято называть черными точками.
Как уже было сказано выше, эта разновидность линий может иметь самопересечения. Наиболее популярным примером замкнутой линии, имеющей самопересечения, является пятиконечная звезда.
Многоугольник как разновидность замкнутой ломаной
Разновидностью описываемой геометрической фигуры является многоугольник. Точками в многоугольнике являются его вершины, а отрезки называются сторонами.
- Если вершины принадлежат одной и той же стороне многоугольника — они носят название смежных.
- Если отрезок соединяет две любых вершины, не являющиеся смежными, он называется диагональю.
- Если у многоугольника имеется n вершин — он называется n-угольником. У такой фигуры имеется количество сторон, равное n.
- Такая ломаная делит плоскость на 2 части — внешнюю и внутреннюю.
- Если точки многоугольника лежат по одну сторону от прямой и проходят через 2 соседние вершины — его принято называть выпуклым.
- Угол выпуклого многоугольника при данной вершине — это угол, который образован двумя его сторонами, для которых эта вершина является общей.
- Внешний угол выпуклого многоугольника при определенной вершине — это угол, смежный с внутренним углом многоугольника при этой же самой вершине.
Примерами многоугольников являются четырехугольники, треугольники, пятиугольники. Рассмотрим подробнее отличительные черты этих фигур.
Треугольник — это геометрическая фигура, которая состоит из трех точек, расположенных не на одной прямой. Эти точки попарно соединяются между собой отрезками.
Четырехугольником в геометрии называется фигура, которая имеет четыре угла и четыре стороны. Четырехугольники встречаются самые разнообразные — это могут быть трапеции, квадраты, параллелограммы, ромбы.
У трапеции параллельны две стороны, которые называются основаниями. Остальные две стороны не параллельны. У параллелограмма между собой параллельны две противоположные стороны.
Отличительной чертой прямоугольника является то, что все его углы прямые. У квадрата являются равными все четыре стороны. Кроме того, все углы у квадрата являются прямыми.
Если у многоугольника все стороны и углы равны, он называется правильным. Такой многоугольник всегда будет выпуклым.
http://budu5.com/manual/chapter/1134
http://4apple.org/schitaetsja-li-treugolnik-lomanoj/
Ломаная линия
- Замкнутая и незамкнутая ломаная
- Самопересекающаяся ломаная
- Длина ломаной
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE
или ломаная EDCBA
.
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
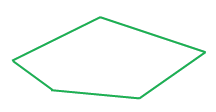
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:
многоугольник ABCDE.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
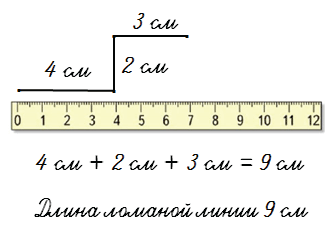
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ответ: 17 см.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Виды линий
- Ломаная линия
Ломаная линия состоит из отрезков — звеньев.
Конец одного отрезка — начало другого. Никакие два соседние звена не лежат на одной прямой.
Концы каждого звена — это вершины. Их можно обозначать буквами.
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Например,
Советуем посмотреть:
Точка. Кривая. Прямая линия
Отрезок. Луч
Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине
Виды линий
Правило встречается в следующих упражнениях:
1 класс
Страница 45,
Моро, Волкова, Степанова, Учебник, часть 1
Страница 93,
Моро, Волкова, Степанова, Учебник, часть 1
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 12. ПР 3. Вариант 1,
Волкова, Проверочные работы
Страница 13. ПР 3. Вариант 2,
Волкова, Проверочные работы
Страница 5,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 107,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 23. Урок 12,
Петерсон, Учебник, часть 2
2 класс
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 38,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 20. ПР 3. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 25. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 16,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 3. Урок 1,
Петерсон, Учебник, часть 2
Страница 112. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 6. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 75,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 109,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33. Урок 13,
Петерсон, Учебник, часть 2
4 класс
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27. Урок 9,
Петерсон, Учебник, часть 1
Длину ломаной можно определить различными способами.
(1) способ.
1. Измерить длину каждого звена с помощью линейки и найти их сумму.
2. На рисунке длина первого звена — (4) см, а длина второго звена — (3) см.
(4 + 3 = 7) см.
Длина ломаной равна (7) см.
(2) способ.
1. Начертить прямую.
2. Отметить точку на прямой.
3. От точки с помощью циркуля отложить последовательно отрезки, равные звеньям ломаной.
4. Измерить длину всего отрезка. Получим, что длина ломаной равна (7) см.
(3) способ.
1. Измерить длину каждого звена с помощью циркуля и линейки:
перенести отрезок, равный длине звена ломаной, на линейку.
2. Найти сумму всех звеньев.
(4 + 3 = 7) см.
Источники:
Рисунки: циркуль, © ЯКласс.
Математика, 2 класс. Урок №13.
Длина ломаной. Закрепление
Перечень вопросов, рассматриваемых в теме:
— Как найти длину ломаной?
Глоссарий по теме:
Ломаная — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего.
Звенья — отрезки, из которых состоит ломаная.
Отрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
Длина ломаной – это сумма длин всех её звеньев.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.32-35
2. Математика. Проверочные работы. 2 кл.: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017 — с.20, 21
3. Математика. Тесты. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017 — с.20, 21, 25
Теоретический материал для самостоятельного изучения
На рисунке мы видим ломаную линию, состоящую из трёх звеньев.
Как найти длину ломаной линии? Это можно сделать двумя способами.
Первый способ. Сначала узнаем длину каждого звена с помощью линейки
Длина первого звена 4 см.
Длина второго звена 6 см.
Длина третьего звена 5 см.
Найдем сумму этих длин.
4+6+5=15 (см)
Найдем длину ломаной вторым способом.
Отложим на прямой один за другим отрезки, равные по длине звеньям ломаной. Это можно сделать с помощью циркуля. Накладываем циркуль на первый отрезок, переносим его на прямую.
Накладываем циркуль на второй отрезок, переносим его на прямую.
Накладываем циркуль на третий отрезок, переносим его на прямую.
Теперь узнаем длину ломаной. Длина ломаной 15 см. В этом случае узнавать длину каждого звена ломаной не надо.
Выводы: длину ломаной можно находить двумя способами.
Первый способ: узнаем длину каждого звена с помощью линейки и найдем сумму этих длин.
Второй способ: с помощью циркуля откладываем на прямой один за другим отрезки, равные по длине звеньям ломаной. Затем измеряем длину всего отрезка. Это и будет длина всей ломаной.
Тренировочные задания.
1. Подчеркните длину ломаной, составленной из трёх звеньев такой длины: 2 см, 3 см и 5 см
Варианты ответов:
10 см 8 см 7 см
Правильный вариант:
10 см 8 см 7 см
2. Расположите ломаные линии по порядку: от самой короткой до самой длинной
Правильный вариант: Найдем длину каждой ломаной
6 + 2 + 2 = 10 см
7 + 5 = 12 см
2 + 1 + 3 +2 = 8 см
3 + 1 + 5 = 9 см
Расставим в порядке возрастания:
2 + 1 + 3 + 2 = 8 см
3 + 1 + 5 = 9 см
6 + 2 + 2 = 10 см
7 + 5 = 12 см