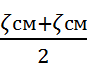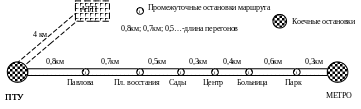Математический расчет пути: как вычислить длину маршрута
Математический расчет пути — это процесс определения длины пути между двумя точками на карте. Этот процесс является важным инструментом в различных областях, от путешествий и географии до инженерии и строительства. В этой статье мы рассмотрим, как можно вычислить длину маршрута с помощью математических методов.
Формула гаверсинусов
Одним из наиболее распространенных методов вычисления длины пути между двумя точками является использование формулы гаверсинусов. Эта формула основана на географических координатах начальной и конечной точек, которые измеряются в градусах.
Формула гаверсинусов выглядит следующим образом:
d = 2r * arcsin(sqrt(sin²((lat2 - lat1)/2) + cos(lat1) * cos(lat2) * sin²((lon2 - lon1)/2)))
где d — расстояние между точками в км, r — радиус Земли в км, lat1 и lat2 — широта начальной и конечной точек соответственно, lon1 и lon2 — долгота начальной и конечной точек соответственно.
Пример использования формулы гаверсинусов: пусть у нас есть две точки с координатами (55.7558° N, 37.6173° E) и (51.5074° N, 0.1278° W). Используем формулу гаверсинусов для определения расстояния между этими точками:
d = 2*6371km*arcsin(sqrt(sin²((51.5074-55.7558)/2) + cos(55.7558) * cos(51.5074) * sin²((-0.1278-37.6173)/2)))
Получаем результат 2 443.67 км.
Формула Винсента
Еще одним методом вычисления длины пути между точками является формула Винсента. Эта формула также основана на географических координатах начальной и конечной точек, но работает с углами в радианах.
Формула Винсента выглядит следующим образом:
d = r * acos( sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2)*cos(lon2-lon1) )
где d — расстояние между точками в км, r — радиус Земли в км, lat1 и lat2 — широта начальной и конечной точек соответственно в радианах, lon1 и lon2 — долгота начальной и конечной точек соответственно в радианах.
Пример использования формулы Винсента: пусть у нас есть две точки с координатами (55.7558° N, 37.6173° E) и (51.5074° N, 0.1278° W). Преобразуем эти координаты в радианы и используем формулу Винсента для определения расстояния между этими точками:
d = 6371km * acos( sin(55.7558*pi/180)*sin(51.5074*pi/180) + cos(55.7558*pi/180)*cos(51.5074*pi/180)*cos((-0.1278-37.6173)*pi/180) )
Получаем результат 2 441.25 км.
Заключение
В этой статье мы рассмотрели два метода вычисления длины пути между двумя точками на карте — формулу гаверсинусов и формулу Винсента. Оба метода используют географические координаты начальной и конечной точек, но имеют различные формулы для вычисления расстояния между ними. Выбор метода зависит от конкретной задачи и требуемой точности.
Пассажирские
перевозки
Вариант№4
Исходные данные:
υтех =
26-0,4 техническая скорость движения.
υтех =
25,6км/час переведём в метры в секунды, υтех=7,1м/с
Номинальная вместимость
автобуса:
gн
= 42-4 = 38 пассажиров.
Определения
длины маршрута по формуле:
Lмар
= υтех*∑tдв;
где: Lмар –
длина маршрута
υтех
– техническая скорость движения
∑tдв –
суммарное время движения по маршруту суммарное время
движения в прямом направлении:
∑tдв =
1787 секунд;
Lмар =
7,1*1787 = 12687,7 метров.
Определим длину и время
в обратном направлении.
∑tдв =1756
секунд;
Lмар =
7,1*1756 = 12467,6 метров
Определим
скорость сообщения.
υсооб
=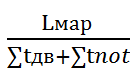
где: ∑tnot
– время промежуточной остановки.
∑tnot
=
234 секунды в прямом направлении
∑tnot
=
212 секунд в обратном направлении
υсооб
= 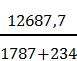
6,2
м/с в прямом направлении
υсооб =
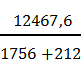
6,3
м/с в обратном направлении
Определим
время стоянки на конечной остановки.
∑tко = 0,1*∑tдв;
∑tко
= 0,1* 1787 = 178,7 секунд для прямого направления
∑tко = 0,1*
1756 = 175,6 секунд для обратного направления
Определим средние время
остановок в прямом и обратном направлении.
t
срnot
=
;
где: n
– количество остановок.
t
срnot
=
=
13,7 секунд для прямого направления
t
срnot
=
=
11,15 секунд для обратного направления
Определим
среднею длину перегона ℓ ср.
ℓ
ср = ;
где: hпер –
число перегонов
ℓ ср
= 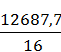
метров для
прямого направления
ℓ
ср = 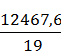
метров для
обратного направления
Определим
коэффициент наполняемости автобуса.
γстt
=
— для
перегона между остановками где: п – количество
перевезенных пассажиров
γстt
= 8,68 для прямого направления
γстt
= 10,52 для обратного направления
γст
= –
для маршрута
γст =
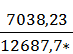
0,55 для прямого направления
γст =
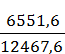
0,52 для обратного направления
Определим коэффициент
сменности пассажиров см
см
= ;
где: Qфак
–
сумма количество перевезенных пассажиров
см
= =
8,76 для прямого направления
см
= =
10,9 для
обратного направления
Определим
среднею длину поездки пассажира ℓпас
ℓпас
=
ℓпас
= 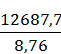
1448 метров в прямом направлении
ℓпас = 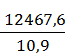
1143 метра в обратном направлении
Определим
время оборота tобр
tобр
= ∑tдв + ∑tдв + ∑tnot
+
∑tnot + ∑tко
tобр
= 1787 + 1756 + 234 + 212 + 354,3 = 4343,3 секунд
Определим
количество рейсов nр
nр
= ;
где: Тмар
время маршрута.
Тмар =
18часов или 64800 секунд
nр
= 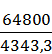
15 рейсов;
Определим
общие количество пассажиров за время маршрута.
Q
= nр *
gн *
*
γстср
γстср
=
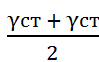
γстср
=
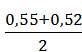
0,53
=
=
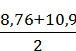
9,83
Q
= 15 * 38 * 9,83 * 0,53 = 2969,6
Производительность
автобуса.
W
= Q * Lмар;
W
= 2969,6 * 25,155 = 74700
Общая
прибыль получаемая с одного автобуса в сутки.
С
= Q *14;
C
= 2969,6 *14 = 41574.4 руб
Общая
прибыль на одно место в сутки.
С
=
;
С = 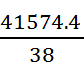
1094 рублей.
Интервал
движения (мин)
Частота
движения (авт./ч)
,
или
Количество
автобусов на маршруте (ед.)
,
или
Время
одного оборота (ч или мин)
Количество
оборотов за день
Подвижность
населения .
Типовая задача
Протяженность
городского диаметрального маршрута 8
км; nпо=16;
t
по=
30 с; t
ко
= 2 мин; маршрут обслуживают 10 автобусов
МАЗ 103;
υт
=24
км/ч. Определить I
и Ч
автобусов на маршруте.
Решение
Время
одного рейса автобуса на маршруте:
Время
одного оборота равно удвоенному времени
рейса:
T0=2×tp
T0
=
2×30
мин = 60 мин, или 1 ч.
Интервал
движения автобусов
I=
60:10 = 6 мин.
Частота
движения:
Ч=
10:1
= 10 авт./ч.
Задачи
41.
Учитывая
пожелания населения, диаметральный
маршрут длиной
8 км продлили еще на 2 км. Таким образом,
на маршруте вместо
20 промежуточных остановок стало
23; tпо
=18
с;
tко
=
4 мин; υт
= 24 км/ч.
1)
Сколько
автобусов надо добавить на маршрут,
чтобы сохранить
I
= 6 мин?
2)
Сколько автобусов потребуется добавить
на маршрут в часы
пик при показателях табл. 18?
42.
На радиальном маршруте протяженностью
10 км
работают
восемь
автобусов
υт
= 25 км/ч; nпo
= 20; tпо
= 30 с; tко
= 6 мин.
Таблица 18
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Первоначальная
Длина |
6 |
7,2 |
8,6 |
9,2 |
10 |
11 |
13 |
12 |
10,5 |
11,5 |
6 |
7,2 |
8,6 |
9,2 |
|
υт |
20 |
21,8 |
22,6 |
23 |
25 |
26 |
27 |
28 |
27,5 |
26,5 |
25 |
26 |
27 |
28 |
|
I |
5 |
7 |
8 |
10 |
6 |
4 |
9 |
10 |
8 |
7 |
8 |
10 |
6 |
4 |
1)
Определить интервал и частоту движения
автобусов на маршруте.
2)
Используя условие задачи 42, рассчитать
I
и Ч
по показателям табл. 19.
Таблица 19
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ам |
4 |
5 |
6 |
7 |
9 |
10 |
3 |
8 |
5 |
4 |
4 |
5 |
6 |
7 |
|
υт |
20 |
21,8 |
22,6 |
23 |
25 |
26 |
27 |
28 |
27,5 |
26,5 |
25 |
26 |
27 |
28 |
|
nпo |
15 |
18 |
22 |
24 |
23 |
21 |
20 |
19 |
17 |
16 |
18 |
22 |
24 |
23 |
43.
На
тангенциальном маршруте работают 15
автобусов; I
=10 мин; υс
= 20 км/ч;
tко
= 3 мин.
1)
Найти длину
маршрута.
2)
Используя
условие задачи, рассчитать длину маршрута
по показателям
табл. 20
Таблица 20
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ам |
4 |
5 |
6 |
7 |
8 |
10 |
12 |
8 |
5 |
4 |
5 |
6 |
7 |
8 |
|
I |
5 |
8 |
6 |
4 |
7 |
4 |
8 |
10 |
5 |
3 |
7 |
4 |
8 |
10 |
|
υс |
22 |
23 |
24 |
25 |
22 |
23 |
24 |
25 |
26 |
23 |
22 |
23 |
24 |
25 |
44.
LM
= 25 км;
υт
=
20 км/ч;
I
=
30 мин.
1) Рассчитать
необходимое количество автобусов на
данном маршруте.
2) Используя
условие задачи рассчитать количество
автобусов на маршруте по показателям
табл. 21.
Таблица 21
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Lм |
15 |
18 |
20 |
28 |
30 |
32 |
35 |
34 |
19 |
33 |
16 |
18 |
19 |
28 |
|
vэ |
16 |
18 |
20 |
21 |
22 |
17 |
19 |
16 |
18 |
19 |
21 |
22 |
17 |
19 |
|
I |
20 |
40 |
45 |
50 |
32 |
34 |
36 |
38 |
22 |
24 |
40 |
45 |
50 |
32 |
45.
Через
остановку
«Автовокзал»
по
маршруту
№ 2 проходит
восемь
автобусов
в 1 ч.
1)
Сколько автобусов работает на маршруте,
если LM
=11 км,
υт
= 22 км/час, nпo
= 22, tпо
= 30 с.,
tко
=
4 мин?
2)
Рассчитать по условию задачи количество
автобусов на маршруте по показателям
табл. 22.
46.
На городском экспрессном маршруте
работают шесть автобусов ЛиАЗ-5256, которые
за день перевозят 12 288 пассажиров; I
=10 мин.
1)
Определить LM
и количество рейсов, если υэ—22
км/ч, γвм
= 0,80, qн
= 110 пассажиров.
2)
Используя условия задачи, рассчитать
LM
и Zр
по показателям табл. 23.
Таблица 22
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
LM |
8 |
10 |
12 |
14 |
6 |
15 |
16 |
13 |
11 |
9 |
10 |
12 |
14 |
6 |
|
nпo |
18 |
20 |
24 |
28 |
15 |
29 |
27 |
26 |
21 |
19 |
24 |
28 |
15 |
29 |
|
υт |
23 |
25 |
26 |
28 |
28 |
29 |
27 |
24 |
29 |
25 |
28 |
28 |
29 |
27 |
Таблица 23
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ам |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
8 |
6 |
9 |
4 |
5 |
7 |
8 |
|
I |
5 |
6 |
7 |
4 |
8 |
9 |
8 |
10 |
5 |
3 |
7 |
4 |
8 |
9 |
|
γвм |
0,76 |
0,82 |
0,88 |
0,92 |
0,8 |
0,9 |
0,79 |
0,87 |
0,85 |
0,75 |
0,92 |
0,8 |
0,9 |
0,79 |
47.
На
городском кольцевом маршруте (рис. 2)
Ч=10
авт./ч;
υт
= 20 км/ч.; tпо=1
мин; tко
=
7
мин.
1) Определить
I
и Ам—
2) Рассчитать
I
и
Ам
по
показателям табл. 24.
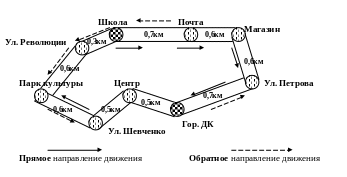
Рис. 2 Схема
городского
кольцевого автобусного
маршрута
Таблица 24
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ч |
8 |
6 |
12 |
7 |
14 |
9 |
11 |
5 |
4 |
10 |
6 |
12 |
7 |
14 |
|
υт |
20,5 |
21,0 |
22,0 |
22,8 |
21,6 |
19,8 |
18,9 |
21,5 |
22,5 |
24 |
22,0 |
22,8 |
21,6 |
19,8 |
|
tко(мин) |
3 |
5 |
8 |
10 |
6 |
7 |
9 |
4 |
3 |
5 |
10 |
6 |
7 |
9 |
48.
Решением
администрации на всех остановках
городского радиального
маршрута
оборудованы соответствующим образом
посадочные площадки,
в результате
чего время tnо
за
один рейс сократилось с 20 до 14 мин.
-
На
сколько увеличатся υс
и
Zр
совершаемые
одним автобусом
за день, если tко
= 6 мин, Lm
=
16 км, υт
= 24 км/час; Тм
=
16,8 ч? -
По
условию задачи рассчитать, на сколько
увеличатся υc
и
Zр
по
показателям табл. 25
Таблица 25
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
LM |
6 |
8 |
10 |
12 |
14 |
5 |
11 |
9 |
10,5 |
11,5 |
8 |
10 |
12 |
14 |
|
υт |
20,5 |
22,8 |
22,8 |
23,2 |
25,4 |
26,2 |
24,9 |
29 |
27 |
26 |
22,8 |
23,2 |
25,4 |
26,2 |
|
Тм |
12 |
14 |
15 |
16 |
13 |
14,5 |
15,5 |
16,5 |
13,8 |
14,2 |
16 |
13 |
14,5 |
15,5 |
49.
Учитывая пожелания пассажиров, интервал
(I)
на городском тангенциальном маршруте
уменьшили с 8 до 6 мин. На маршруте при I
= 8 мин работают 10 автобусов при I
=6 мин – 13 автобусов той же марки, которые
за день перевозят 62 тыс. пассажиров; qн
=
55 пассажиров; ηсм
= 3,8; Тм
= 16 час.
1)
Определить, как изменится увм
автобуса?
2) По условию задачи
рассчитать, как изменится увм
по
показателям табл.26
Таблица 26
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ам |
4 |
5 |
6 |
6 |
8 |
7 |
9 |
12 |
11 |
10 |
6 |
8 |
7 |
9 |
|
Тм |
12,1 |
14,6 |
15,3 |
16,8 |
18,1 |
13,2 |
11,8 |
10,9 |
14,1 |
17 |
12,1 |
14,6 |
15,3 |
16,8 |
|
ηсм |
3,1 |
4,3 |
3,25 |
4,4 |
2,8 |
5,0 |
4,9 |
3,9 |
3,33 |
4,2 |
4,3 |
3,25 |
4,4 |
2,8 |
50.
Пригородный маршрут протяженностью 40
км обслуживают
восемь автобусов, которые движутся с I
= 30 мин; nпo
= 8; tпо=
2 мин; tко
= 6 мин. Определить
υт
,
υэ
и
υc.
51.
Междугородный
маршрут обслуживают 10 автобусов,
которые работают с I
=1 час.
1) Сколько
оборотных Zр
будет
сделано,
если
известно, что Тм
= 20 час.?
2) Используя
условия задачи, рассчитать, сколько Zр
будет
выполнено показателям
табл.
27
Таблица 27
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Тм |
14 |
16 |
16,8 |
19,5 |
21 |
22 |
20,6 |
14,5 |
16,5 |
21,5 |
16 |
16,8 |
19,5 |
21 |
|
I |
0,5 |
0,8 |
1,2 |
0,6 |
1,1 |
0,4 |
0,7 |
0,9 |
0,8 |
0,5 |
1,2 |
0,6 |
1,1 |
0,4 |
|
Ам |
5 |
6 |
8 |
7 |
8 |
4 |
6 |
4 |
6 |
5 |
7 |
8 |
4 |
6 |
52.
Среднее расстояние перевозки пассажиров
уменьшилось с 5,7 до 4,8 км.
1) Насколько
увеличится количество перевезенных за
день пассажиров,
если LM=10
км, маршрут обслуживают автобусы с qн
= 62 пассажира, каждый
автобус делает на маршруте за день 25
рейсов,
при увм
= 0,80?
2) Используя
условия задачи, рассчитать, насколько
увеличится
количество перевозимых за день на
маршруте пассажиров по показателям
табл. 28?
53.
Восемь
автобусов обслуживают междугородный
маршрут протяженностью 80 км, Ч—
2авт/ч,
ТМ=16
ч, средняя
длина ездки одного пассажира 20,8 км, γвм
= 0,86, qBM
=
34
пассажира.
1)
Определить
количество пассажиров, которые будут
перевезено этими автобусами за день
2)
Рассчитать
количество пассажиров,
перевезенных на маршруте за день, по
показателям табл.29.
Таблица 28
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Zp |
10 |
12 |
15 |
18 |
20 |
22 |
24 |
21 |
19 |
17 |
12 |
15 |
18 |
20 |
|
LM |
8 |
12 |
15 |
18 |
7 |
11 |
14 |
13 |
16 |
17 |
15 |
18 |
7 |
11 |
|
γвм |
0,76 |
0,78 |
0,8 |
0,86 |
0,9 |
0,85 |
0,75 |
0,69 |
0,77 |
0,87 |
0,86 |
0,9 |
0,85 |
0,75 |
Таблица 29
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Ч |
3 |
3,5 |
3,8 |
2,2 |
2,6 |
2,8 |
2,5 |
3,6 |
3,7 |
2,7 |
3,5 |
3,8 |
2,2 |
2,6 |
|
lср |
8 |
10 |
16 |
20 |
5 |
11 |
14 |
13 |
16 |
17 |
16 |
20 |
5 |
11 |
|
Ам |
5 |
6 |
7 |
10 |
8 |
9 |
11 |
12 |
5 |
10 |
10 |
8 |
9 |
11 |
Рис. 3 Схема
городского
тангенциального автобусного
маршрута
54.
Городской тангенциальный маршрут
обслуживают пять автобусов
qн
= 62
пассажира;
γвм
= 0,70; Тм
=12
ч; I
=
8 мин. За это время они перевозят 12 500
пассажиров
(рис. 3)
-
Определить
среднее расстояние перевозки пассажиров?
-
Используя
условие задачи, рассчитать среднее
расстояние перевозки
пассажиров на маршруте по показателям
табл. 30
55.
Учитывая
пожелания трудящихся, время работы
автобусов
на городском маршруте продлили с 15,84 до
18 ч.
-
На
сколько рейсов больше стали делать
автобусы за день, еслиυэ
=18
км/ч, Lм
= 8 км, на маршруте работают шесть
автобусов? -
Рассчитать,
используя условия задачи, насколько
рейсов больше
стали делать автобусы за день по
показателям табл. 31.
Таблица
30
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
I |
4 |
5 |
6 |
7 |
9 |
10 |
12 |
8 |
9 |
7 |
5 |
6 |
7 |
9 |
|
Тм |
14 |
16 |
13 |
11 |
15 |
16,5 |
14,5 |
13,5 |
11,8 |
12 |
13 |
11 |
15 |
16,5 |
|
γвм |
0,78 |
0,82 |
0,68 |
0,72 |
0,84 |
0,88 |
0,65 |
0,75 |
0,79 |
0,77 |
0,72 |
0,84 |
0,88 |
0,65 |
Таблица 31.
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Lм |
3 |
4 |
4,5 |
5 |
6 |
6,5 |
5,5 |
3,5 |
7 |
7,5 |
4 |
4,5 |
5 |
6 |
|
υэ |
18,5 |
20 |
20,8 |
19,3 |
21,4 |
20,5 |
19,8 |
20,1 |
19,6 |
18,8 |
20,8 |
19,3 |
21,4 |
20,5 |
|
Ам |
4 |
5 |
7 |
8 |
10 |
9 |
11 |
12 |
5 |
10 |
10 |
9 |
11 |
12 |
56.
Для лучшего обслуживания пассажиров
на городском тангенциальном маршруте
протяженностью 14 км ввели экспрессное
сообщение автобусов.
1) На сколько
сократится tр
экспрессных автобусов, если υт
= 28 км/ч,
nnо
= 20, среднее
tnо
=1 мин, tко
= 4 мин?
2) Используя условия
задачи, рассчитать, на сколько сократится
время рейса (tр
)по показателям табл. 32.
Таблица 32
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Lм |
5 |
4 |
3,8 |
6,5 |
7 |
8 |
10 |
9 |
8,5 |
9,5 |
4 |
3,8 |
6,5 |
7 |
|
υт |
22 |
22,8 |
23,5 |
24 |
24,6 |
22,5 |
24,1 |
25 |
23,8 |
24,1 |
23,5 |
24 |
24,6 |
22,5 |
|
nnо |
4 |
5 |
7 |
8 |
10 |
9 |
11 |
12 |
5 |
10 |
8 |
10 |
9 |
11 |
57.
Интервал автобусов на
пригородном маршруте –
I
= 20 мин.
1)
1Сколько nnо
на маршруте, если υт
=25 км/час.;
tnо
=1 мин; tко
= 3 мин.
Маршрут обслуживают шесть автобусов;
Lm
—20
км.
2)
Используя
условия задачи 57, рассчитать, сколько
nnо
на маршруте
по показателям табл. 33.
Таблица 33
|
Показатели |
Варианты |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
Lм |
15 |
22 |
18 |
24 |
28 |
30 |
32 |
23 |
25 |
27 |
22 |
18 |
24 |
28 |
|
I |
30 |
40 |
45 |
36 |
25 |
35 |
45 |
24 |
38 |
32 |
45 |
36 |
25 |
35 |
|
υт |
21 |
24 |
28 |
30 |
22 |
23 |
32 |
33 |
35 |
25 |
30 |
22 |
23 |
32 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени
от t1 до t2.
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d x}{d t}right)^{2}+left(frac{d y}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}} d t(1)$$
В цилиндрических координатах длина пути может быть выражена как:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d rho}{d t}right)^{2}+left(rho frac{d varphi}{d t}right)^{2}+left(frac{d z}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}} d t(2)$$
В сферических координатах формулу длины пути запишем:
$$s=int_{t_{1}}^{t_{2}} sqrt{left(frac{d r}{d t}right)^{2}+left(r frac{d theta}{d t}right)^{2}+left(r sin theta frac{d varphi}{d t}right)^{2}} d t=int_{t_{1}}^{t_{2}} sqrt{(dot{r})^{2}+(r dot{theta})^{2}+(r varphi sin theta)^{2}} d t(3)$$
Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением.
Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t rightarrow 0$ материальная точка проходит путь ds,
который называют элементарным. При этом:
$$d s=|d bar{r}|=v d t$$
где $bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=vleft(t_{2}-t_{1}right)(5)$$
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути
$Delta s$ на отрезке времени от
$t$ до
$t + Delta t$ находят как:
$$Delta s=langle vrangle Delta t(6)$$
где $langle vrangle$ – средняя путевая скорость. При равномерном движении
$langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+frac{a t^{2}}{2}(7)$$
где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
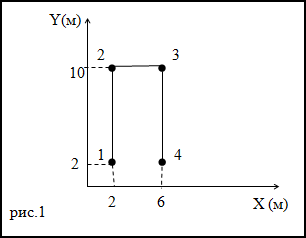
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой,
чему равно перемещение, если точка двигалась 1-2-3-4.
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 — 2 = 4 (m)$$
Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$
Ответ. Путь равен 20 м, перемещение равно 4 м.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией:
x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения
задачи примем формулу пути в виде:
$$s=int_{t_{1}}^{t_{2}} sqrt{(dot{x})^{2}} d t(2.1)$$
Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c leq t leq 5 c$ имеем:
$$s=int_{0}^{5} sqrt{left(-0,2 frac{dleft(t^{2}right)}{d t}right)^{2}} d t=0,left.4 cdot frac{t^{2}}{2}right|_{0} ^{5}=5(m)$$
Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.
Расчёт расстояния по времени и скорости
Определение расстояния
Расстояние это длина от одного объекта до другого. Измеряется в км, м, дм, см и.т.д.
Формула расстояния
S=V×t
где V — скорость движения на протяжении всего пути,
t — время за которое этот путь был пройден
Выберите что хотите посчитать
Введите скорость V
Введите время
Ед. измерения ответа
Правила ввода
Вводить в поля калькулятора можно целые числа и десятичные дроби — 1, 2, 3, 4, 5, 0.1, 2.5 и.т.д.
В калькуляторе можно задать единицы измерения вводных данных и единицы измерения ответа.
Похожие калькуляторы