Задания
Версия для печати и копирования в MS Word
Тип 12 № 311544 
i
Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле 
где 
— длина нити (в метрах). Пользуясь данной формулой, найдите длину нити маятника, период колебаний которого составляет 7 с.
Спрятать решение
Решение.
Выразим длину маятника:
Подставляя, получаем:
Ответ: 12,25.
Аналоги к заданию № 46: 311544 337952 338064 … Все
Источник: ГИА-2012. Математика. Контрольная работа.(1 вар)
Спрятать решение
·
Прототип задания
·
Помощь
1
габбас
[215K]
4 года назад
Если известен период колебаний математического маятника, то длину маятника можно подсчитать по известной формуле периода математического маятника Т=2*пи*корень квадратный из( L/g), где g=9,8 м/с2 — ускорение свободного падения на Земле (приблизительно). Оттуда длина маятника L = (Т^2*g)/(4*пи^2) = (1*9,8)/(4*3,14*3,14) = 9,8/39,48 = 0,248 м или примерно 25 см.
Ответ: 25 см.
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Главная
»
Самолетостроение
»
Физика
»
Колебания математического и физического маятника
Колебания математического и физического маятника
Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.
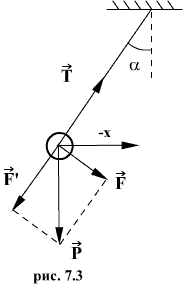
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 
, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 
и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
Момент силы относительно точки О: 
, и момент инерции:
M = FL .
Момент инерции J в данном случае
Угловое ускорение:
С учетом этих величин имеем:
или
 |
(7.8) |
Его решение
,
Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.
Физический маятник.
Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения
. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:
 |
(7.10) |
 |
(7.11) |
Решение этого уравнения
Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 
или
.
Из этого соотношения определяем
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
1. Математический
маятник – модель состоит из материальной
точки подвешенной не длине невесомой
и нерастяжимой нити совершающей колебания
в вертикальной плоскости под действием
силы тяжести.
При
движении материальной точки совершается
вращательное
движение относительно
оси проходящей через точку подвеса О.
Так как линия
действующего натяжения нити проходит
через ось
вращения то ее
момент относительно оси равен 0.
На Ох:
.
При малых углах отклонения от
вертикали,можно считать чтоsinα≈α.
Решением этого
уравнения является функция вида:
—
математический маятник совершает
колебания по гармоническому закону.
-период
колебания математического маятника не
зависит от массы маятника, а зависит от
его длины и ускорения свободного падения
в том месте где подвешен маятник.
2. Физическим
маятником называется твердое тело,
закрепленное на неподвижной горизонтальной
ocи (оси подвеса), не проходящей через
центр тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести. В отличие от математического
маятника массу такого тела нельзя
считать точечной.
Считая
колебания малыми положим чтоsinφ=φ,
тогда
—
дифференциальное уравнение гармонических
колебаний решением которого является
.Период
физического маятника
.Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического маятника,
т.е. 
или
Из этого соотношения
определяем
.
Данная формула определяет приведенную
длину физического маятника, т.е. длину
такого математического маятника, период
колебаний которого равен периоду
колебаний данного физического маятника.
Вопрос 43. Затухающие
колебания. Дифференциальное уравнение
затух колеб и его решение. Логарифмический
дискремент и коэффициет затухания.
Затухающие
колебания – это колебания, амплитуда
которых из-за потерь энергии реальной
колебательной системы с течением времени
уменьшается.
Дифференциальное
уравнение свободно затухающих колебаний
линейной системы задаётся в виде:
,
где х – колеблющаяся величина, описывающая
тот или иной физический процесс,
β=b/2m=const
– коэффициент затухания, ω0
– циклическая частота свободных
незатухающих колебаний той же колебательной
системы, т.е. при β =0 (при отсутствии
потерь энергии) называется собственной
частотой колебательной системы. Решение
дифференциального уравнения затухающих
элементов:
Сделаем
Подставляем
найденное вместе с выражением для х и
после сокращения на
. 1)Если
то решение этого Д/У имеет вид
.
Начальная амплитуда колебаний А и
начальная фаза φ зависит от способа
возбуждения колебаний. Решением этого
уравнения являются затухающие колебания
.
Периодом затухающих колебаний называется
промежуток времени между двумя последними
выражениями колебательной системы от
положения равновесия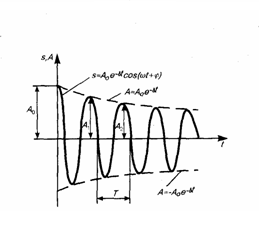
.
ЕслиA(t)
и A(t+T)
– амплитуды двух последовательных
колебаний, соответствующих моментам
времени, отличающимся на период, то
отношение:
называется декрементом затухания, а
его логарифм
— логарифмическим
декрементом затухания; Ne
– число колебаний, совершаемых за время
уменьшения амплитуды в e
раз. Логарифмический декремент затухания
– постоянная для каждой колебательной
системы величина. 2) если
—
в этом случае понятие периода теряет
смысл- апериодический характер.