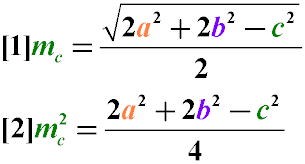Как найти длину медианы зная стороны треугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

Задача.

Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

Дано: ∆ ABC,

BC=a, AC=b, AB=c,

сторона AC — наибольшая,

BO- медиана.

Найти: BO.

Решение:

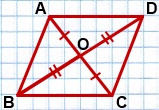
1) На луче BO отложим отрезок OD, OD=BO.

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

4) По свойству диагоналей параллелограмма,

$[A{C^2} + B{D^2} = 2(A{B^2} + A{D^2})]$

$[{b^2} + B{D^2} = 2({a^2} + {c^2})]$

$[B{D^2} = 2({a^2} + {c^2}) - {b^2}]$

$[BD = sqrt {2({a^2} + {c^2}) - {b^2}} ]$

так как BO=1/2 BD (по построению),

$[underline {BO = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} .} ]$

Если ввести обозначение

$[BO = {m_b},]$

формула для нахождения медианы треугольника по его сторонам примет вид:

$[{{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} }]$

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

$[{m_a} = frac{1}{2}sqrt {2({b^2} + {c^2}) - {a^2}} ]$

$[{m_c} = frac{1}{2}sqrt {2({a^2} + {b^2}) - {c^2}} ]$

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Чтобы по сторонам треугольника найти медиану, не обязательно запоминать дополнительную формулу. Достаточно знать алгоритм решения.

Для начала рассмотрим задачу в общем виде.

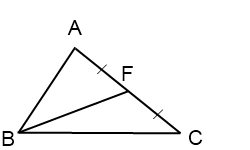
Дан треугольник со сторонами a, b, c. Найти длину медианы, проведенной к стороне b.

AB=a, AC=b, BC=c.

Решение.

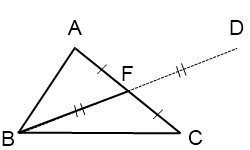
На луче BF отложим отрезок FD, FD=BF.

Соединим точку D с точками A и C.

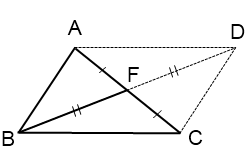
Четырехугольник ABCD — параллелограмм (по признаку), так как у него диагонали в точке пересечения делятся пополам.

Свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

Отсюда: AC²+BD²=2(AB²+BC²), значит, b²+BD²=2(a²+c²),

BD²=2(a²+c²)-b². По построению, BF — половина BD, следовательно,

$[BD = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]$

Это — формула нахождения медианы треугольника по его сторонам. Обычно ее записывают так:

$[{m_b} = frac{1}{2}sqrt {2({a^2} + {c^2}) - {b^2}} ]$

Переходим к рассмотрению конкретной задачи.

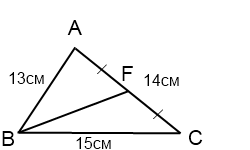
Стороны треугольника равны 13 см, 14 см и 15 см. Найти медиану треугольника, проведенную к его средней по длине стороне.

Решение:

Применяя аналогичные рассуждения, получаем:

AC²+BD²=2(AB²+BC²).

Отсюда

14²+BD²=2(13²+15²)

BD²=2(169+225)-196=592

$[BF = frac{1}{2}DD = frac{1}{2} cdot 4sqrt {37} = 2sqrt {37} (cm)]$

Ответ:

Источник

Из какой вершины треугольника опустить медиану:

Из вершины A

Из вершины B

Из вершины C

Укажите размеры:

AB
AC
BC

A
B
C

Сторона AB

Сторона AC

Сторона BC

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Так как каждая вершина треугольника имеет свою медиану, то всего в треугольнике может быть три медианы.

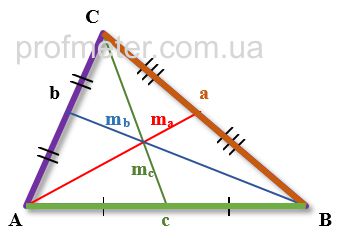
Длину медианы треугольника ABC если известны все стороны треугольника можно расчитать по одной из нижепреведённых формуле:

Формула медианы

m
a
b
c

A
B
C

m_a = sqrt{ dfrac{2b^2 + 2c^2 -a^2}{4} }

A, B, C — вершины треугольники
a, b, c — стороны треугольника
m_a — медиана треугольника опущенная из вершины A

a
b
c

A
B
C

m_b = sqrt{ dfrac{2a^2 + 2c^2 -b^2}{4} }

m_b — медиана из вершины B

a
b
c

A
B
C

m_c = sqrt{ dfrac{2a^2 + 2b^2 -c^2}{4} }

m_c — медиана из вершины C

Так же данные формулы можно встретить в такой записи, что по сути является тем же самым что формулы выше:

m_a = 0.5 cdot sqrt{ 2b^2 + 2c^2 — a^2 }

m_b = 0.5 cdot sqrt{ 2a^2 + 2c^2 — b^2 }

m_c = 0.5 cdot sqrt{ 2a^2 + 2b^2 — c^2 }

Длина медианы треугольника

Воскресенье, 20 октября, 2019

Очень часто в ЕГЭ, ОГЭ и других экзаменах по математике встречаются задачи, в которых требуется найти длину медианы треугольника, если известны его стороны. Это действительно возможно, ведь длины трёх сторон треугольника полностью его определяют. В данной статье профессиональный репетитор по математике и физике объясняет, как это можно сделать.

Вопрос о том, как найти длину медианы треугольника, если известны все стороны треугольника, действительно имеет смысл. Ведь треугольник определяется длинами его сторон. То есть нет двух разных треугольников с одинаковыми сторонами. По третьему признаку равенства треугольников это должны быть два равных треугольника. Это означает, что если мы знаем все стороны в треугольнике, то мы можем найти в нём все основные элементы. В том числе и длины всех медиан. Разберёмся, как находится длина медианы треугольника.

Изобразим треугольник ABC. Обозначим его стороны маленькими буквами , и , причём сторона пусть лежит напротив угла A, сторона — напротив угла B и сторона — напротив угла C. Это стандартное обозначение, которое часть используется в учебниках по геометрии. Проведём также медиану AM, которая разделит сторону BC на два равных отрезка, длины которых составляют по $dfrac{1}{2}a$ . Обозначим длину этой медианы , имея в виду, что эта медиана проведена именно к стороне :

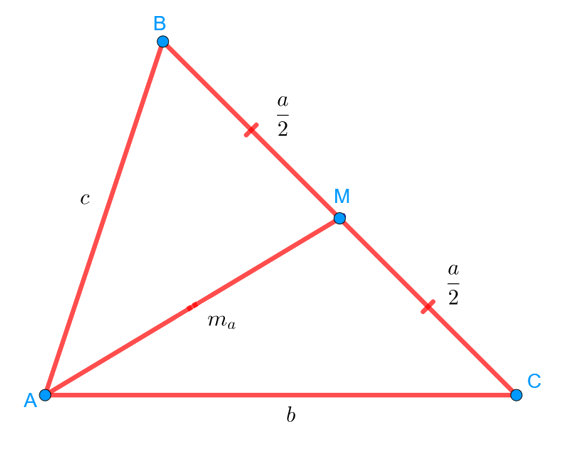
То есть — это длина медианы треугольника, которую нам нужно найти. Наша задача состоит в том, чтобы выразить её через длины сторон треугольника , и .

Ну и идея состоит в том, чтобы использовать стандартное в таких случаях дополнительное построение, которое условно называют «удвоением медианы». Продлим медиану AM за точку M на отрезок MD, равный по длине медиане AM. То есть длина отрезка MD тоже равна . Как это нам поможет? Дело в том, что, соединив точку D c точками B и C, мы получаем четырёхугольник ABDC, который в действительности является параллелограммом:

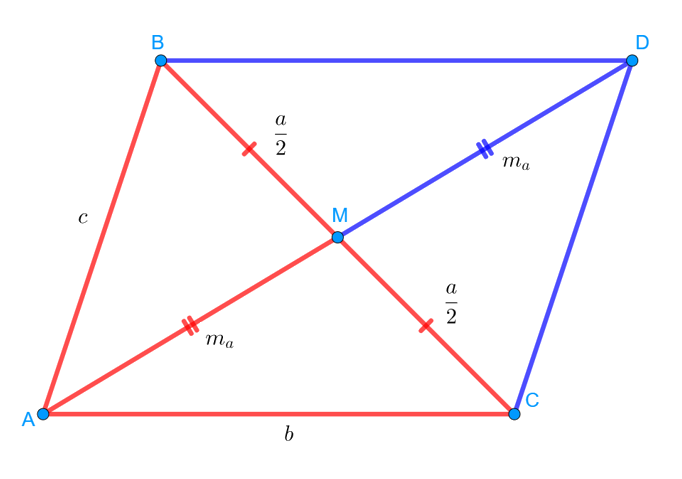
Удвоение медианы в треугольнике ABC, которое приводит к достраиванию его до параллелограмма

Естественно! Ведь есть такой признак. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. Здесь у нас получается ровно эта ситуация. M — середина AD, и одновременно — середина BC. Значит, ABDC — параллелограмм. Это означает, в частности, что BD = b, а DC = c, так как противоположные стороны параллелограмма равны.

Ну а дальше действовать можно по-разному. Но поскольку у всех всегда разный уровень знаний по геометрии, то я постараюсь обойтись в дальнейшем самыми известными фактами из геометрии. Я имею в виду теорему Пифагора. Я думаю, что вы все прекрасно её знаете. Ну или хотя бы про неё слышали.

Итак, проведём высоты нашего параллелограмма BF и DH. Обозначим длины этих высот буквой . А вот отрезочки AF и CH обозначим за . Они будут одинаковые по длине, потому что равны прямоугольные треугольники ABF и CDH. Они, конечно же, равны, ведь у них равны гипотенузы AB и CD, а также катеты BF и DH:

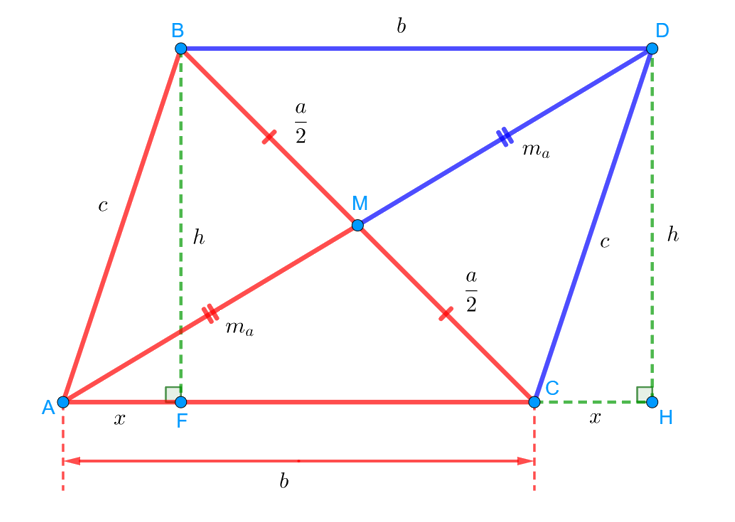
Нахождение длины медианы треугольника по известным длинам его сторон

Ну а теперь рассмотрим прямоугольный треугольник BFC. Запишем для него теорему Пифагора:

(1) $begin{equation*} BC^2 = BF^2+FC^2 = a^2 = h^2+(b-x)^2 end{equation*}$

Аналогично для прямоугольного треугольника ADH получаем по теореме Пифагора:

(2) $begin{equation*} AD^2 = DH^2+AH^2 = 4m_a^2=h^2+(b+x)^2 end{equation*}$

Ну и для прямоугольного треугольника ABF по теореме Пифагора получаем:

(3) $begin{equation*} AB^2 = BF^2+AF^2 = c^2=h^2+x^2 end{equation*}$

То есть получается три уравнения. Нужно их использовать, чтобы найти . Как же это сделать? Во-первых, сложим вместе уравнения (1) и (2), раскроем скобки и приведём подобные слагаемые. В результате получаем следующее выражение:

Ну и теперь осталось использовать уравнение (3), только сперва нужно умножить обе части этого уравнения на 2. Тогда получим, что . Ну и тогда мы получаем выражение , из которого получаем окончательно:

$[ m_a = dfrac{1}{2}sqrt{2c^2+2b^2-a^2} ]$

Вот искомая формула, которую мы не просто записали, но ещё и доказали. Но ирония заключается в том, что запоминать её совсем не обязательно. Лучше просто знать, как её вывести, и получать её каждый раз при решении каждой конкретной задачи.

Задавайте свои вопросы по математике и физике в комментариях. Здесь на сайте и на моём Youtube-канале. На самые часто задаваемые вопросы я отвечу в следующих видео и статьях. Всего доброго!

Репетитор по математике и физике Сергей Валерьевич

Источник

Примечание. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Почти наверняка курс будет дополнен.

Задача. Найти длину медианы треугольника через его стороны

Стороны треугольника равны 8, 9 и 13 сантиметров. К наибольшей стороне треугольника проведена медиана. Определите медиану треугольника исходя из размеров его сторон.

Решение.

Задача имеет два способа решения. Первый, который не нравится учителям средней школы, но является наиболее универсальным.

Способ 1.

Применим Теорему Стюарта, согласно которой квадрат медианы равен одной четвертой от суммы удвоенных квадратов сторон из которой вычли квадрат стороны, к которой проведена медиана.

m_c² = ( 2a² + 2b² — c² ) / 4

Соответственно

m_c² = ( 2 * 8² + 2 * 9² — 13²) / 4
m_c² = 30,25
m_c = 5,5 см

Способ 2.

Второй способ решения, который преподаватели в школе любят — это дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.

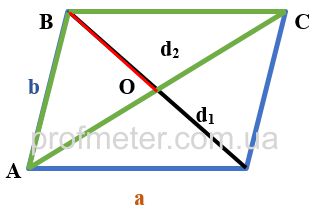
Продлим стороны треугольника и медиану достроив их до параллелограмма. В этом случае медиана BO треугольника ABC будет равна половине диагонали получившегося параллелограмма, а две стороны треугольника AB, BC — его боковым сторонам. Третья сторона треугольника AC, к которой была проведена медиана, является второй диагональю получившегося параллелограмма.

Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.

2(a²+b²)=d₁²+d₂²

Обозначим диагональ параллелограмма, которая образована продолжением медианы исходного треугольника как х, получим:

2( 8² + 9² ) = 13² + x²
290 = 169 + x²
x² = 290 — 169
x² = 121
х = 11

Поскольку искомая медиана равна половине диагонали параллелограмма, то величина медианы треугольника составит 11 / 2 = 5,5 см

Ответ: 5,5 см

Медиана треугольника |

Описание курса

| Нахождение площади через медианы

Источник

Формула медианы

Похожие калькуляторы:

Длина медианы треугольника

Задача. Найти длину медианы треугольника через его стороны