Геометрия является разделом математики, изучающим структуры в пространстве и отношение между ними. В свою очередь она также состоит из разделов, и одним из них является стереометрия. Она предусматривает изучение свойств объемных фигур, находящихся в пространстве: куба, пирамиды, шара, конуса, цилиндра и др.
Конус – это тело в евклидовом пространстве, которое ограничивает коническая поверхность и плоскость, на которой лежат концы ее образующих. Его образование происходит в процессе вращения прямоугольного треугольника вокруг любого из его катетов, поэтому он относится к телам вращения.
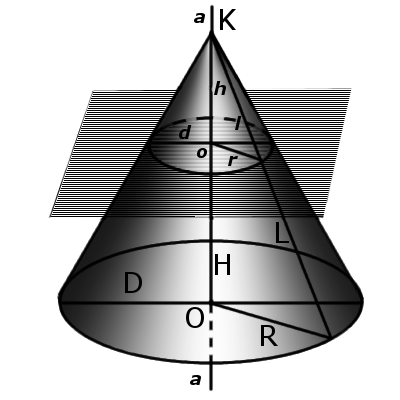
Составляющие конуса
Различают следующие виды конусов: косой (или наклонный) и прямой. Косым называется тот, ось которого пересекается с центром его основания не под прямым углом. По этой причине высота в таком конусе не совпадает с осью, так как она является отрезком, который опущен из вершины тела на плоскость его основания под углом 90°.

Тот конус, ось которого расположена перпендикулярно к его основанию, называется прямым. Ось и высота в таком геометрическом теле совпадают по причине того, что вершина в нем расположена над центром диаметра основания.
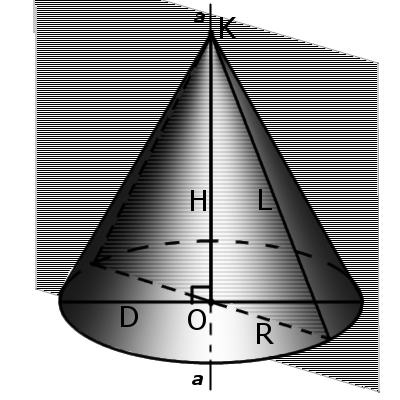
Конус состоит из следующих элементов:
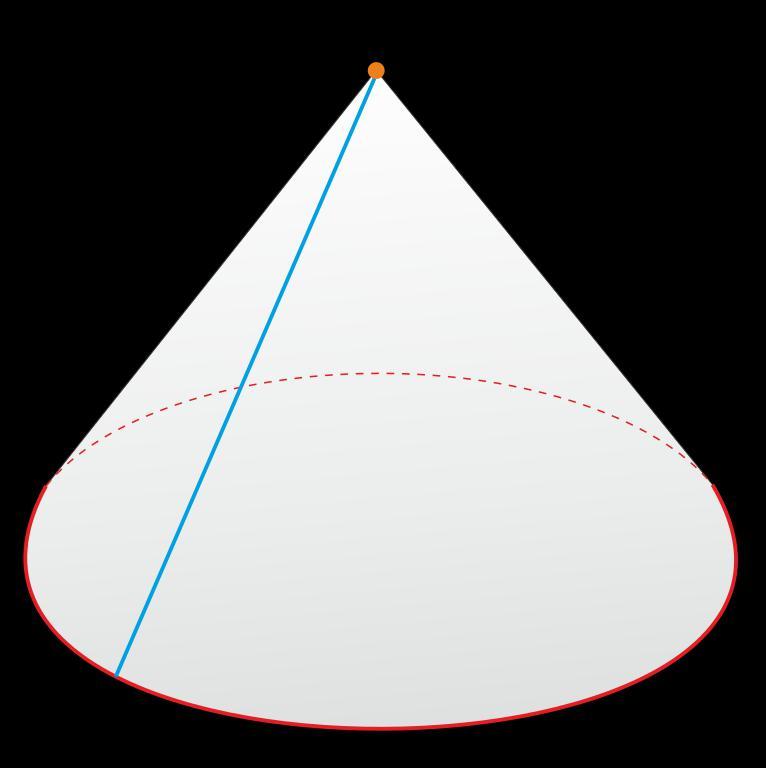
Все эти отрезки являются образующими конуса. Они наклонные к основанию геометрического тела, и в случае прямого конуса их проекции равны, так как вершина равноотдалена от точек круга основания. Таким образом, можно сделать вывод, что в правильном (прямом) конусе образующие равны, то есть имеют одинаковую длину и образуют одинаковые углы с осью (или высотой) и основанием.

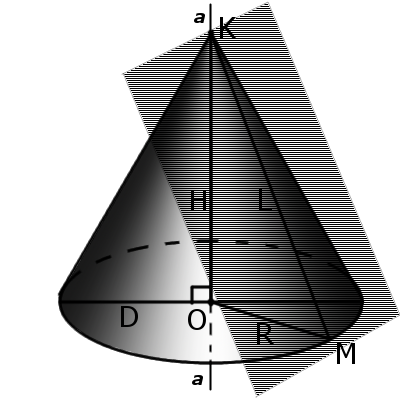
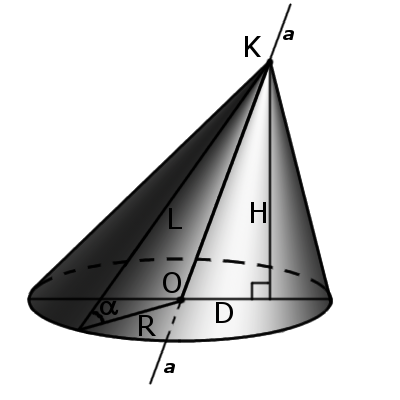
Так как в косом (или наклонном) теле вращения вершина смещена по отношению к центру плоскости основания, образующие в таком теле имеют разную длину и проекцию, поскольку каждая из них находится на разном расстоянии от двух любых точек круга основания. Кроме того, углы между ними и высотой конуса также будут отличаться.
Длина образующих в прямом конусе
Как написано ранее, высота в прямом геометрическом теле вращения перпендикулярна плоскости основания. Таким образом, образующая, высота и радиус основания создают в конусе прямоугольный треугольник.
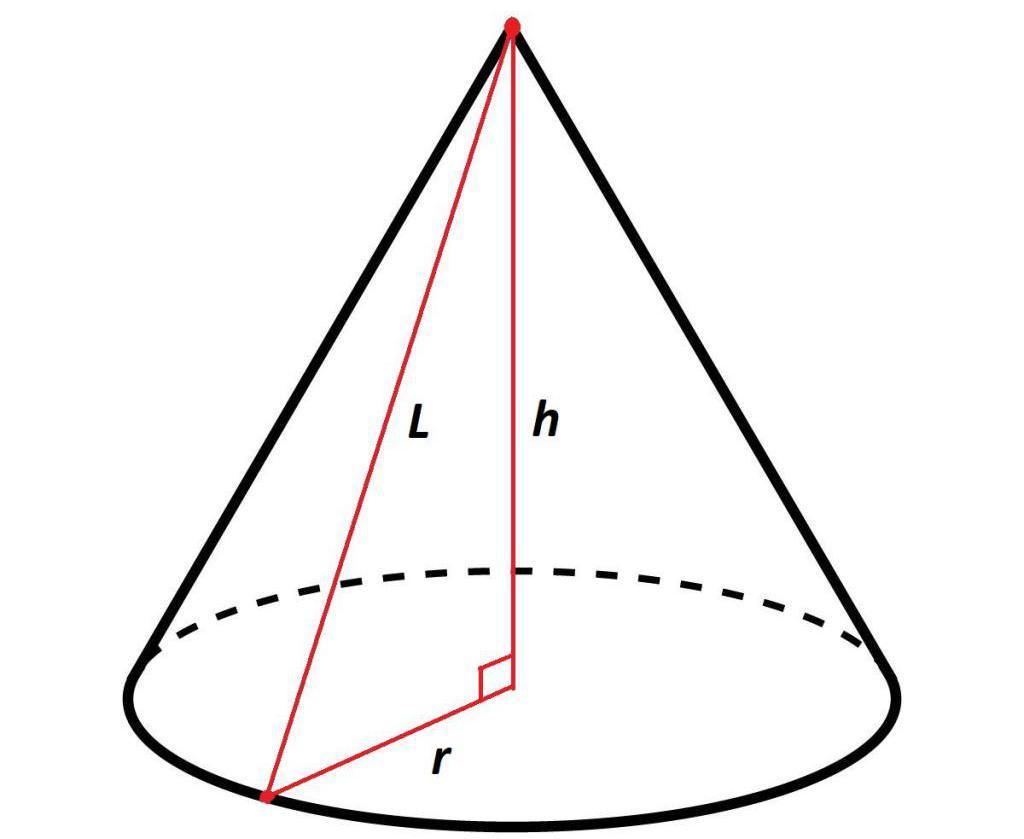
То есть, зная радиус основания и высоту, при помощи формулы из теоремы Пифагора, можно вычислить длину образующей, которая будет равна сумме квадратов радиуса основания и высоты:
l2 = r2+ h2 или l = √r2 + h2
где l – образующая;
r – радиус;
h – высота.
Образующая в наклонном конусе
Исходя из того, что в косом, или наклонном конусе образующие имеют не одинаковую длину, рассчитать их без дополнительных построений и вычислений не получится.
Прежде всего необходимо знать высоту, длину оси и радиус основания.
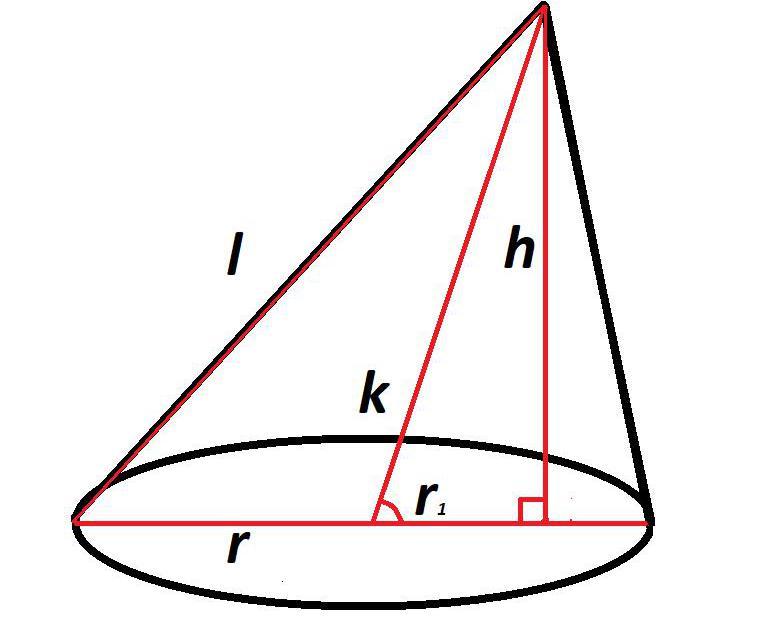
Имея эти данные, можно рассчитать часть радиуса, лежащую между осью и высотой, по формуле из теоремы Пифагора:
r1= √k2 — h2
где r1 – это часть радиуса между осью и высотой;
k – длина оси;
h – высота.
В результате сложения радиуса (r) и его части, лежащей между осью и высотой (r1), можно узнать полную сторону прямоугольного треугольника, сформированного образующей конуса, его высотой и частью диаметра:
R = r + r1
где R – катет треугольника, образованного высотой, образующей и частью диаметра основания;
r – радиус основания;
r1 – часть радиуса между осью и высотой.
Пользуясь все той же формулой из теоремы Пифагора, можно найти длину образующей конуса:
l = √h2+ R2
или, не производя отдельно расчет R, объединить две формулы в одну:
l = √h2 + (r + r1)2.
Несмотря на то, прямой или косой конус и какие вводные данные, все способы нахождения длины образующей всегда сводятся к одному итогу — использованию теоремы Пифагора.
Сечение конуса
Осевым сечением конуса называется плоскость, проходящая по его оси либо высоте. В прямом конусе такое сечение представляет собой равнобедренный треугольник, в котором высотой треугольника является высота тела, его сторонами выступают образующие, а основание – это диаметр основания. В равностороннем геометрическом теле осевое сечение является равносторонним треугольником, так как в этом конусе диаметр основания и образующие равны.
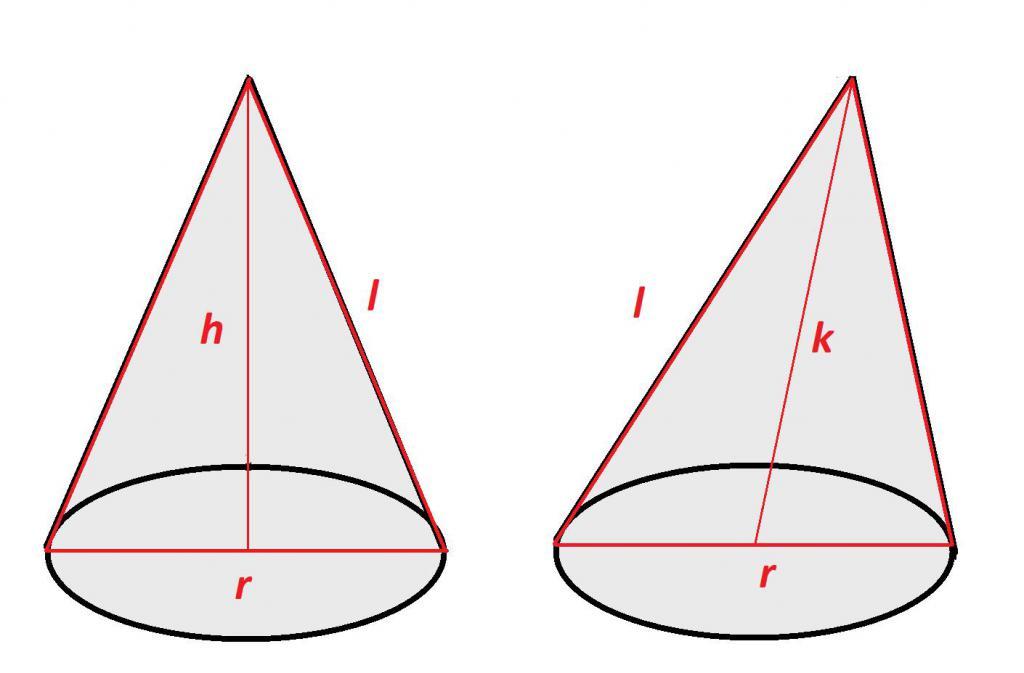
Плоскость осевого сечения в прямом конусе является плоскостью его симметрии. Причиной этому служит то, что его вершина находится над центром его основания, то есть плоскость осевого сечения делит конус на две одинаковые части.
Так как в наклонном объемном теле высота и ось не совпадают, плоскость осевого сечения может не включать в себя высоту. Если осевых сечений в таком конусе можно построить множество, так как для этого необходимо соблюдать лишь одно условие — оно должно проходить только через ось, то осевое сечение плоскости, которому будет принадлежать высота этого конуса, можно провести лишь одно, потому что количество условий увеличивается, а, как известно, две прямые (вместе) могут принадлежать только одной плоскости.
Площадь сечения
Упомянутое ранее осевое сечение конуса представляет собой треугольник. Исходя из этого, его площадь можно рассчитать по формуле площади треугольника:
S = 1/2 * d * h или S = 1/2 * 2r * h
где S – это площадь сечения;
d – диаметр основания;
r – радиус;
h – высота.
В косом, или наклонном конусе сечение по оси также является треугольником, поэтому в нем площадь сечения рассчитывается аналогично.
Объем
Поскольку конус является объемной фигурой в трехмерном пространстве, то можно вычислить его объем. Объемом конуса называется число, которое характеризует это тело в единице измерения объема, то есть в м3. Расчет не зависит от того, прямой он или косой (наклонный), так как формулы для двух этих видов тел не отличаются.
Как указано ранее, образование прямого конуса происходит вследствие вращения прямоугольного треугольника по одному из его катетов. Наклонный же, или косой конус образуется иначе, поскольку его высота смещена в сторону от центра плоскости основания тела. Тем не менее такие отличия в строении не влияют на методику расчета его объема.
Расчет объема
Формула объема любого конуса выглядит следующим образом:
V = 1/3 * π * h * r2
где V – это объем конуса;
h – высота;
r – радиус;
π — константа, равная 3,14.
Для того чтобы рассчитать обьем конуса, необходимо иметь данные о высоте и радиусе основания тела.

Для расчета высоты тела необходимо знать радиус основания и длину его образующей. Поскольку радиус, высота и образующая объединяются в прямоугольный треугольник, то высоту можно рассчитать по формуле из теоремы Пифагора (a2+ b2= c2 или в нашем случае h2+ r2= l2, где l – образующая). Высота при этом будет рассчитываться путем извлечения квадратного корня из разности квадратов гипотенузы и другого катета:
a = √c2- b2
То есть высота конуса будет равна величине, полученной после извлечения квадратного корня из разности квадрата длины образующей и квадрата радиуса основания:
h = √l2 — r2
Рассчитав таким методом высоту и зная радиус его основания, можно вычислить объем конуса. Образующая при этом играет важную роль, так как служит вспомогательным элементом в расчетах.
Аналогичным образом, если известна высота тела и длина его образующей, можно узнать радиус его основания, извлекая квадратный корень из разности квадрата образующей и квадрата высоты:
r = √l2 — h2
После чего по той же формуле, что указана выше, рассчитать объем конуса.
Объем наклонного конуса
Так как формула объема конуса одинакова для всех видов тела вращения, отличие в его расчете составляет поиск высоты.
Для того чтобы узнать высоту наклонного конуса, вводные данные должны включать длину образующей, радиус основания и расстояние между центром основания и местом пересечения высоты тела с плоскостью его основания. Зная это, можно с легкостью рассчитать ту часть диаметра основания, которая будет являться основанием прямоугольного треугольника (образованного высотой, образующей и плоскостью основания). После чего, снова используя теорему Пифагора, произвести расчет высоты конуса, а впоследствии и его объема.
Поскольку радиус конуса характеризует размер его основания, то зная его, можно найти диаметр, длину окружности и площадь круга, лежащего в основании. Диаметр представляет собой удвоенный радиус, длина окружности – удвоенный радиус, умноженный на число π, а площадь круга – квадрат радиуса, умноженный на число π.
d=2r
P=2πr
S_(осн.)=πr^2
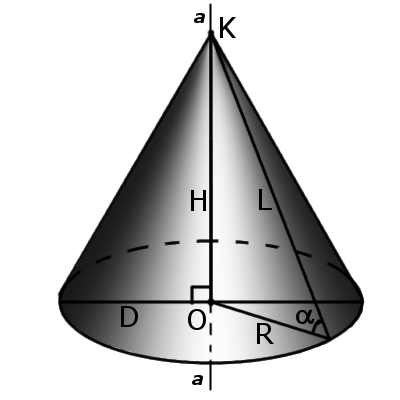
Зная радиус и образующую конуса, можно уже найти его высоту, угол между образующей и основанием, угол раствора конуса. Высота конуса через радиус и образующую ищется по теореме Пифагора в прямоугольном треугольнике, оттуда же можно вычислить и угол β через тригонометрические отношения сторон. Угол α можно найти из равнобедренного треугольника, образованного двумя образующими и диаметром, отняв из 180 градусов два угла β. (рис.40.1, 40.2)
h=√(l^2-r^2 )
cosβ=r/l
α=180°-2β
Площадь боковой поверхности конуса равна произведению полупериметра основания на образующую или произведению числа π на радиус и образующую. Чтобы найти площадь полной поверхности, зная радиус и образующую конуса, необходимо прибавить к площади боковой поверхности произведение числа π на квадрат радиуса, что является площадью основания конуса.
S_(б.п.)=πrl
S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)
Объем конуса, также как и объем пирамиды рассчитывается как одна треть основания, умноженная на высоту.
V=1/3 S_(осн.) h=(πr^2 h)/3
Радиус сферы, вписанной в конус, вычисляется как произведение высоты на радиус конуса, деленное на сумму радиуса и образующей. Радиус сферы, описанной вокруг конуса, представляет собой отношение квадрата образующей к удвоенной высоте. (рис.40.3, 40.4)
r_1=hr/(l+r)=(r√(l^2-r^2 ))/(l+r)
R=l^2/2h
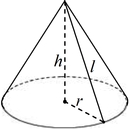
Конус – это геометрическая фигура, полученная вращением прямоугольного треугольника вокруг одного из катетов. У каждого конуса есть основание и боковая поверхность.
Любой конус характеризуется высотой h (осевой линией), радиусом r и образующей l (см. рисунок). Именно эти характеристики используются в формулах конуса при вычислении объема, площади поверхности и площади боковой поверхности.
Высота конуса (осевая линия) – это перпендикуляр, проведенный из вершины конуса к основанию.
Радиус конуса – это радиус его основания.
Образующая конуса – это отрезок, который соединяет вершину конуса с любой точкой, лежащей на линии окружности основания.
Формула образующей конуса
Образующую конуса можно найти, зная ее высоту H и радиус R:
L = √H2 + R2
Формула площади боковой поверхности конуса
Площадь боковой поверхности конуса можно получить, зная его радиус R и образующую L:
Sбок.пов = πRL
Формула площади основания конуса
Площадь основания конуса можно вычислить по его радиусу R:
Sосн = πR2
Формула площади конуса
Площадь поверхности конуса можно получить, сложив площадь боковой поверхности и площадь основания конуса:
S = Sбок.пов + Sосн = πRL + πR2
Формула объема конуса
Объем конуса можно вычислить, зная его высоту H и площадь основания:
V = 1/3 ⋅ Sосн ⋅ H = 1/3πR2H
Элементы конуса
Определение. Вершина конуса — это точка (K), из которой исходят лучи.
Определение. Основание конуса — это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.
Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.
Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):
L2 = R2 + H2
Определение. Направляющая конуса — это кривая, которая описывает контур основания конуса.
Определение. Боковая поверхность конуса — это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.
Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.
Определение. Высота конуса (H) — это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.
Определение. Ось конуса (a) — это прямая, проходящая через вершину конуса и центр основания конуса.
Определение. Конусность (С) конуса — это отношение диаметра основания конуса к его высоте. В случае усеченного конуса — это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:
где C — конусность, D — диаметр основания, d — диаметр меньшего основания и h — расстояние между основаниями.
Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:
где R — радиус основы, а H — высота конуса.
Определение. Осевое сечение конуса — это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника — это диаметр основания конуса.
Определение. Касательная плоскость к конусу — это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.
Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).
Определение. Прямой конус — это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.
Формула. Объём кругового конуса:
где R — радиус основы, а H — высота конуса.
Формула. Площадь боковой поверхности (Sb) прямого конуса через радиус R и длину образующей L:
Sb = πRL
Формула. Общая площадь поверхности (Sp) прямого кругового конуса через радиус R и длину образующей L:
Sp = πRL + πR2
Определение. Косой (наклонный) конус — это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.
Формула. Объём любого конуса:
где S — площадь основы, а H — высота конуса.
Определение. Усеченный конус — это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.
Формула. Объём усеченного конуса:
где S1 и S2 — площади меньшей и большей основы соответственно, а H и h — расстояние от вершины конуса до центра нижней и верхней основы соответственно.
Уравнение конуса
1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | — | z2 | = 0 |
| a2 | a2 | c2 |
2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):
| x2 | + | y2 | = | z2 |
| a2 | b2 | c2 |
Основные свойства кругового конуса
1. Все образующие прямого кругового конуса равны между собой.
2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.
3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.
4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).
6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).
7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).
8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.
Конус является объемной фигурой вращения, которая часто появляется в геометрических задачах. Как и всякая фигура, он обладает рядом линейных характеристик, площадью поверхности и объемом. В данной статье рассмотрим, что представляет собой конус, а также приведем формулу образующей конуса.
Конус в геометрии
Многие ели в жаркий летний день мороженое-рожок. Вафельный стаканчик этого мороженого имеет форму конуса. В геометрии более строгое определение этой фигуры следующее: конус представляет собой поверхность, которая получается в результате соединения с помощью прямых отрезков всех точек некоторой плоской кривой с фиксированной точкой пространства, не лежащей в плоскости упомянутой кривой. Если кривая является эллипсом, то конус будет эллиптическим, если окружностью — то круглым и так далее.
Данное выше геометрическое определение соответствует фигуре на рисунке ниже.
Здесь кривой, на которую опирается коническая поверхность, является окружность, центр которой лежит на вертикальной оси. Как видно из рисунка, хотя фигура является пространственной, но ее объем равен нулю. Если вместо окружности взять круг, тогда ограниченный этим кругом и конической поверхностью объем пространства будет объемом конуса.
Элементы фигуры
Перед тем как привести формулу образующей конуса, следует пояснить, из каких элементов состоит рассматриваемая пространственная фигура, и какие геометрические понятия используются для ее описания.
Ориентируясь на предыдущий рисунок, можно сказать, что конус образован двумя поверхностями:
- конической, которая называется также боковой;
- плоской фигурой (круг на рисунке), которая называется основанием конуса.
В отличие от полиэдров, конус не имеет граней и ребер, однако у него имеется одна единственная вершина, которая сверху ограничивает коническую поверхность. На предыдущем рисунке вершина находится в начале координат.
Для рассматриваемой фигуры также используют понятия образующей и направляющей. Что такое образующая конуса, и что такое его направляющая. Начнем с определения последней. Направляющей является кривая, ограничивающая основание фигуры. Названа она так, поскольку вдоль нее движется образующая, описывая коническую поверхность. Направляющая часто называется директрисой.
Образующая — это прямой отрезок, который соединяет вершину фигуры и любую точку направляющей. Образующих у конуса бесконечное множество. Их совокупность определяет коническую поверхность. Образующую также называют генератрисой.
Круглый прямой конус
Как отмечалось выше, основание конуса может быть ограничено любой плоской кривой. Тем не менее на практике и в геометрических задачах часто встречается круглый конус. Его и будем рассматривать далее в статье.
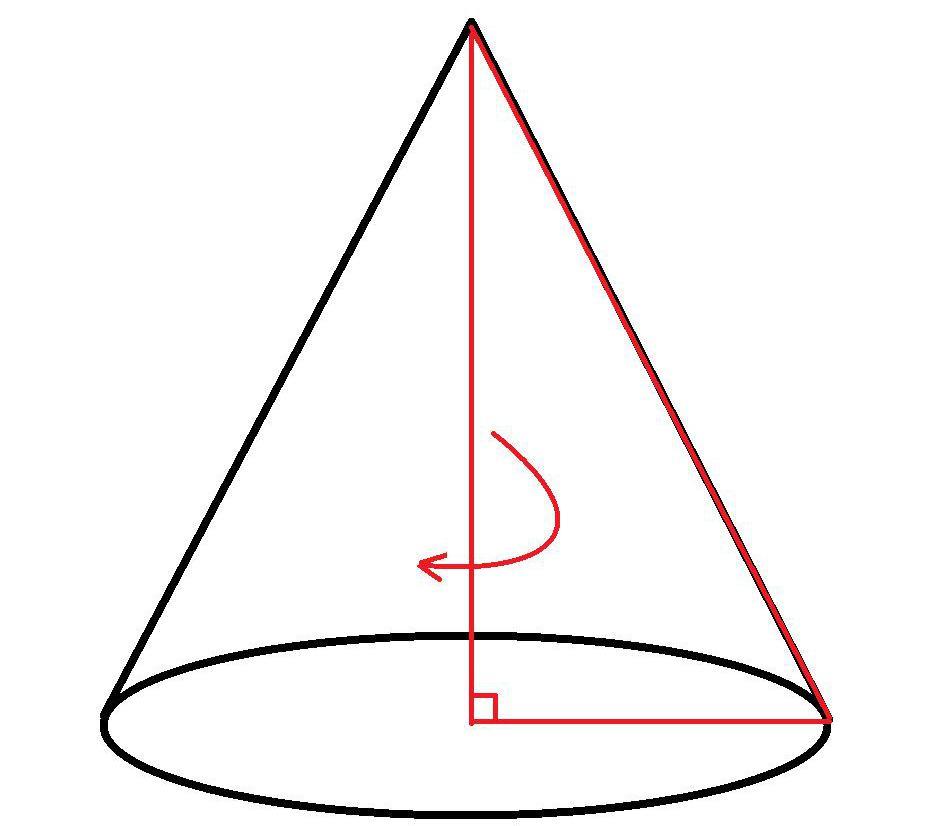
Круглый конус может быть прямым или наклонным. В первом случае перпендикуляр, проведенный из его вершины к основанию, пересекает последнее в центре круга. Прямой круглый конус является симметричной фигурой вращения, которую можно получить с помощью прямоугольного треугольника. Рисунок ниже показывает, как это делается.
На рисунке показан прямоугольный треугольник, который стоит на одном из своих катетов. Вокруг другого катета, являющегося осью, происходит вращение плоской фигуры. Во время вращения гипотенуза треугольника описывает коническую поверхность.
Линейные характеристики круглого прямого конуса
Ниже показан чертеж круглого конуса, на котором введены обозначения. Величина h — это высота фигуры, r — круглого основания радиус, который называется радиусом конуса, s — длина образующей.
Очевидно, что все образующие s рассматриваемой фигуры имеют одинаковую длину. Это важное свойство присуще только прямому круглому конусу. Угол между любой образующей и осью вращения конуса является постоянной величиной при известных значениях r и h.
Как видим из рисунка, стороны r, h и s ограничивают прямоугольный треугольник. Этот факт позволяет применить теорему Пифагора для записи математического равенства, связывающего названные линейные характеристики конуса. Равенство имеет форму:
s2 = r2 + h2
Это равенство содержит ответ на вопрос о том, как найти длину образующей конуса. Если известны радиус фигуры и ее высота, тогда:
s = √(r2 + h2)
Далее, на примерах решения задач покажем, как пользоваться формулой образующей конуса.
Задача с площадью конической поверхности и длиной окружности основания
Дан прямой конус с круглым основанием. Известно, что площадь его боковой поверхности равна 120 см2, а длина окружности основания составляет 30 см. Чему равна образующая конуса?
Решение этой задачи предполагает использование двух дополнительных формул, которые не были рассмотрены в статье. Приведем их ниже:
Sb = pi × r × s;
L = 2 × pi × r
Первое выражение — это формула для вычисления площади конической поверхности Sb. Второе выражение знакомо каждому школьнику, это формула для определения длины окружности L.
Выражаем радиус r из второго выражения, подставляем его в первое:
r = L / (2 × pi);
Sb = pi × L / (2 × pi) × s
Тогда искомая формула длины образующей конуса примет вид:
s = 2 × Sb / L
Подставляем данные площади Sb и длины L в эту формулу, получаем ответ: s = 8 см.
Задача с площадью основания и высотой
Известно, что круглое основание конуса имеет площадь 40 см2. Высота фигуры в 2 раза больше диаметра этого основания. Необходимо найти длину генератрисы конуса.
Как и в предыдущем случае, запишем два уравнения, опираясь на условие задачи:
So = pi × r2;
h = 4 × r
Первая формула — это известное выражение для площади круга. Второе равенство следует из того факта, что высота больше в 2 раза диаметра, а значит, в 4 раза радиуса r.
Оба выражения позволяют через So выразить r и h:
r = √(So / pi);
h = 4 × √(So / pi)
Теперь воспользуемся формулой образующей конуса через h и r. Получаем:
s = √(So / pi + 16 × So / pi) = √(17 × So / pi)
Подставляем величину So в равенство и записываем ответ: s ≈ 14,72 см.
Просмотры: 19