Как найти длину образующей усеченного конуса равна

План урока:

Понятие цилиндра

Понятие конуса

Усеченный конус

Понятие цилиндра

Построим на некоторой плоскости α окружность L, центр которой находится в точке О, а ее радиус обозначим как r. Далее через каждую точку этой окруж-ти проведем прямую, которая будет перпендикулярна к α. Все вместе эти прямые образуют поверхность, которую принято называть цилиндрической поверхностью (может использоваться сокращение поверх-ть). Введем несколько понятий:

• Окружность, построенная в плос-ти α, именуется основанием цилиндрической поверх-ти;
• Каждая прямая, проходящая через эту окруж-ть L и перпендикулярная α – это образующая цилиндрической поверх-ти;
• Прямая, проходящая через точку О и также перпендикулярная α, именуется осью цилиндрической поверх-ти.

Примечание. Заметьте, что в стереометрии при изображении окружности на плос-ти она выглядит как эллипс (овал).

Заметим, что так как все образующие и ось цилиндрической поверх-ти перпендикулярны одной и той же плос-ти α, то они будут параллельны друг другу.

Далее проведем плос-ть β, параллельную α. Так как образующие и ось пересекали α, то они должны пересекать и β. В результате они образуют в плос-ти β какую-то плоскую линию L₁. Докажем, что L₁ – это также окружность.

Действительно, пусть ось цилиндрической поверх-ти пересекает плос-ти α и β в точках О и О₁ соответственно. Произвольная образующая пересекает эти же плос-ти в точках А и А₁:

Так как ОО₁||АА₁, то ОО₁А₁А – это плоский четырехугольник. ОО₁⊥α и ОО₁⊥β, поэтому углы ∠АОО₁ и ∠А₁О₁О – прямые. АА₁⊥α и АА₁⊥β, поэтому прямыми будут и углы ∠ОАА₁ и ∠О₁А₁А. Получается, что ОО₁А₁А – это прямоугольник, и поэтому отрезки ОА и О₁А₁ одинаковы:

Итак, точка А₁ находится на расстоянии r от О₁. Аналогично и для любой другой точки на линии L₁ можно показать, что она находится на расстоянии r от О₁. То есть все точки L₁ равноудалены от О₁, и поэтому L₁ – это окруж-ть с центром в точке О₁, ч. т. д.

Обратите внимание, что окруж-ти L и L₁ имеют одинаковые радиусы, то есть это одинаковые окруж-ти.

Объемная фигура, образованная окруж-тями L и L₁, именуется цилиндром. Рассмотрим его основные элементы:

• круги L₁ и L – это основания цилиндра;
• отрезок ОО₁ – ось цилиндра;
• отрезки образующих, заключенные между основаниями, именуются образующими цилиндра;
• часть цилиндрической поверх-ти, заключенную между основаниями цилиндра, именуют боковой поверхностью цилиндра.

Напомним, что отрезки параллельных прямых, заключенные между параллельными плос-тями, имеют одинаковую длину. Отсюда вытекает тот факт, что образующие цилиндра одинаковы.

Введем ещё два термина:

• длина образующей именуется высотой цилиндра;
• радиус оснований цилиндра именуется радиусом цилиндра.

Отметим, что на самом деле мы рассмотрели только частный случай цилиндра – так называемый прямой круговой цилиндр. Его основания – это круги (поэтому он именуется круговым), а его образующие образуют с основаниями прямой угол(поэтому он именуется прямым). Можно построить наклонный цилиндр (его также называют косым), у которого образующие не перпендикулярны основанию. Также существуют и цилиндры, у которых основаниями являются не окруж-ти, а другие фигуры, например параболы:

В принципе любую призму (а значит и любой параллелепипед) можно считать цилиндром. Однако в дальнейшем в курсе школьной стереометрии под цилиндром будет подразумеваться исключительно прямой круговой цилиндр, если специально не оговорено иное.

В реальной жизни очень многие предметы имеют форму цилиндра. Колонны в зданиях, ножки стульев, бочки, рулоны бумаги представляют собой цилиндры. Даже дерево можно условно считать цилиндром.

Рассмотрим сечение цилиндра плос-тью, перпендикулярной его основаниям.

Пусть сечение пересекает нижнее основание цилиндра в точках А₁ и В₁. Тогда перпендикуляры к основанию, проходящие через эти точки, будут принадлежать этому сечению. Но эти перпендикуляры – одновременно и образующие цилиндра А₁А и В₁В. Значит, сечение проходит и через точки А и В. Раз АА₁ и ВВ₁ – перпендикуляры к обоим основаниям цилиндра, то

Итак, в четырехугольнике АВВ₁А₁ все углы прямые, то есть он представляет собой прямоугольник. Более того, можно утверждать, что любое сечение, проходящее через образующую цилиндра, будет прямоугольником, ведь такое сечение будет перпендикулярно основаниям, так как оно содержит перпендикуляр к ним. Сечение, проходящее через цилиндрическую ось, именуется осевым сечением. Оно также имеет форму прямоугольника.

Далее рассмотрим сечение цилиндра плос-тью, параллельной основаниям:

Пусть секущей будет плос-ть γ, а нижнее основание располагается в плос-ти α. Тогда по определению фигура, «зажатая» между этими двумя плос-тями – это цилиндр, а потому сечение должно иметь форму круга. Получается, что сечение γ разбивает цилиндр на два цилиндра.

Рассмотрим боковую поверх-ть цилиндра. Она представляет собой замкнутую поверхность. Если ее условно «разрезать» по образующей цилиндра и развернуть, то получится прямоугольник:

Длина одной стороны такого прямоугольника (он называется разверткой боковой поверх-ти цилиндра) – это длина образующей цилиндра, то есть его высота. Длина второй стороны совпадает с длиной окруж-ти, лежащей в основании цилиндра. Если радиус цилиндра обозначен как r, то длина этой окруж-ти составляет 2πr. Тогда площадь боковой поверх-ти можно рассчитать как площадь прямоугольника:

Площадь полной поверх-ти цилиндра – это сумма площадей его оснований и его боковой поверх-ти. Так как площадь круга рассчитывается по формуле

Рассмотрим ещё несколько важных понятий. В цилиндр может быть вписана прямая призма. В таком случае основания призмы находятся в тех же плос-тях, что и основания цилиндра, а её боковые грани – это образующие цилиндра.

Если плос-ть содержит образующую цилиндра, но не пересекает его основания, то такая плос-ть именуется касательной к цилиндру. Можно сказать, что касательная плос-ть – это такая плос-ть, которая имеет ровно по одной общей точке с каждым основанием цилиндром.

Если каждая боковая грань призмы – это касательная к цилиндру, а основания призмы находятся в тех же плос-тях, что и основания цилиндра, то говорят, что цилиндр вписан в призму.

Естественно, что если цилиндр вписан в призму, то его основания оказываются вписанными в те многоугольники, которые являются основаниями призмы. Если же призма вписана в цилиндр, то основания цилиндра – это уже окруж-ти, описанные около этих многоугольников.

Рассмотрим несколько задач, в которых фигурируют цилиндры.

Задание. Найдите боковую и полную площади цилиндра, если его радиус составляет 2 м, а высота – 3 м.

Задание. Какова длина диагонали осевого сечения цилиндра, с высотой 4 м и радиусом 1,5 м?

Решение. Осевое сечение цилиндра – это прямоугольник, обозначим его как АВСD. Сторона АВ – это высота цилиндра, а AD – это диаметр нижнего основания, ведь AD проходит через центр окруж-ти О. Тогда длина AD вдвое больше радиуса цилиндра:

Задание. Осевое сечение цилиндра – это квадрат, площадь которого обозначена буквой Q. Какова площадь основания цилиндра?

Решение. Обозначим сторону сечения-квадрата буквой а. Зная площадь сечения, легко найдем и сторону:

Задание. Высота цилиндра составляет 8 см, а его радиус – 5 см. Через его образующую проведено сечение, которое имеет форму квадрата. Каково расстояние между этим сечением и осью цилиндра?

Решение. Обозначим сечение как АВСD. Так как и это сечение, и ось цилиндра перпендикулярны основаниям цилиндра, то они должны быть параллельны друг другу. Расстояние между ними – это длина перпендикуляра О₁К, опущенного из центра основания на сторону ВС:

Отрезок АВ имеет длину 8 см, ведь это высота цилиндра. Так как АВСD – квадрат, то и ВС имеет такую же длину. ВС – это хорда в окруж-ти с центром в точке О₁. Напомним, что перпендикуляр к хорде, опущенный из центра окруж-ти, делит ее пополам, поэтому

 

Задание. Диаметр цилиндра равен его высоте. На верхнем основании, центр которого находится в точке О, отмечены точки А и В так, что ∠АОВ составляет 60°. Отрезок АА₁ – образующая цилиндра. Найдите тангенс угла ∠ВА₁А.

Решение. Рассмотрим ∆АОВ. Он равнобедренный, ведь радиусы АО и ОВ одинаковы. Но если в равнобедренном треугольнике один из углов составляет 60°, то и все углы будут также будут по 60°, то есть это равносторонний треугольник. Тогда, если радиус цилиндра обозначен как r, то

Понятие конуса

Построим на плос-ти α окруж-ть L с центром в точке О. Далее через О проведем перпендикуляр к α и отметим на нем точку Р. Если мы отрезками соединим точку Р с каждой точкой окруж-ти L, то получим поверх-ть, которая именуется конической поверхностью. При этом:

• прямая ОР – это ось конической поверх-ти;
• прямые, соединяющие Р с точками на окруж-ти L, именуются образующими конической поверх-ти;
• сама точка Р – это вершина конической поверх-ти.

Объемное тело, ограниченное окруж-тью L и конической поверх-тью, именуется конусом. Соответственно вершина конической поверх-ти, её ось и образующие будут одновременно являться вершиной, осью и образующими конуса. Окруж-ть L – это основание конуса.

Ещё несколько терминов:

• коническая поверх-ть конуса именуется его боковой поверх-тью;
• если же к этой площади прибавить ещё и площадь основания, то в итоге получится полная площадь конуса;
• отрезок ОР – это не только ось конуса, но и высота конуса.

Как и в случае с цилиндром, мы в данном случае рассматриваем особый случай конуса – прямой круговой конус. В более общем случае ось конуса может не быть перпендикуляром к плос-ти основания (так называемый косой конус). Также в его основании может находиться не окруж-ть, а другая плоская фигура.

В общем случае любая пирамида может рассматриваться как частный случай конуса. Однако в рамках школьного курса под конусом подразумевается исключительно прямой круговой конус, если только не обговорено иное.

Докажем важное утверждение:

Действительно, рассмотрим две произвольные образующие РА и РВ у конуса с вершиной Р, у которой О – центр основания:

Так как ось ОР перпендикулярна основанию, то ∆РОА и ∆РОВ – прямоугольные. У них общий катет РО, а катеты АО и ОВ одинаковы как радиусы окруж-ти. Тогда ∆РОА и ∆РОВ равны, поэтому одинаковы и образующие РА и РВ, ч. т. д.

Заметим, что конус получается при вращении прямоугольного треуг-ка вокруг его катета. Так, на следующем рисунке конус получается при вращении ∆РОА с прямым углом О относительно катета РО:

Если сечение конуса проходит через его ось, то оно именуется осевым сечением. Ясно, что это сечение будет являться треуг-ком, причем две его стороны – это образующие конуса, а третья сторона диаметр основания. Образующие конуса одинаковы, поэтому осевое сечение будет равнобедренным треуг-ком.

Теперь рассмотрим сечение, параллельное плос-ти основания. Пусть оно пересекает ось РО в какой-то точке О₁. Также пусть А₁ – точка пересечения образующей АР исходного конуса с секущей плос-тью α:

Заметим, что раз ось РО перпендикулярна основанию, то она также будет перпендикулярна и секущей плос-ти, ведь основание и плос-ть α параллельны. Тогда ∠РО₁А₁ будет прямым.

Теперь рассмотрим ∠РОА и ∠РО₁А₁. Они прямоугольные и у них есть общие угол ∠АРО. Значит, это подобные треуг-ки. Обозначим радиус ОА как r, а длину А₁О₁ как r₁. Тогда из подобия получаем:

Рассмотрим теперь другую образующую ВР, которая пересекает секущую плос-ть в точке В₁. Отрезки АО и ОВ одинаковы. Повторяя предыдущие рассуждения, легко доказать подобие ∆РОВ и ∆РО₁В₁, откуда можно вычислить длину О₁В₁:

Получили, что точки А₁и В₁ находятся на одинаковом расстоянии r₁ от точки О₁. Мы выбрали точки А и В произвольно, поэтому для любых двух точек, принадлежащих сечению конуса, можно утверждать, что они равноудалены от точки О₁. Это значит, что все точки сечения лежат на окруж-ти с центром в точке О₁ и радиусом r₁, то есть сечение имеет форму окруж-ти.

Как определить площадь боковой поверхности конуса? Для этого ее надо «разрезать» вдоль одной из образующих и развернуть на плос-ти. В результате получится круговой сектор.

Напомним, что площадь сектора может быть рассчитана по формуле

Теперь обозначим длину образующей буквой l, а радиус основания конуса как r. Тогда

Для вычисления полной площади конуса к боковой поверх-ти необходимо добавить ещё и площадь основания:

Усеченный конус

Ранее мы уже изучали сечение конуса плос-тью, параллельной его основанию. Такое сечение разбивает конус на две фигуры. Одна из них – это конус меньших размеров, а вторая именуется усеченным конусом:

Введем несколько понятий и отметим очевидные факты:

• боковая поверхность усеченного конуса – это коническая поверх-ть;
• у усеченного конуса есть два основания, имеющих форму окруж-ти;
• те отрезки образующих конической поверх-ти, которые заключены между основаниями усеченного конуса, именуются образующими усеченного конуса;
• отрезок, соединяющий центры оснований, именуется высотой усеченного конуса, или его осью.

В предыдущем параграфе мы уже выяснили, что радиусы оснований усеченного конуса связаны с высотами исходного конуса и того конуса, который получается при проведении секущей плос-ти:

Заметим, что любые две образующие усеченного конуса одинаковы. Действительно, пусть усеченный конус с образующими АА₁ и ВВ₁ получен их исходного конуса с образующими АР и ВР:

Заметим, что осевое сечение усеченного конуса – это равнобедренная трапеция:

Действительно, построим осевое сечение исходного конуса, которое пройдет через образующие РА и РВ. Пусть эти образующие пересекают плос-ть верхнего основания усеченного конуса в точках А₁ и В₁ соответственно. Тогда АА₁В₁В будет осевым сечением усеченного конуса. Точки А, А₁, В₁ и В располагаются в одной плос-ти РАВ, то есть АА₁В₁В – плоский четырехугольник. Его стороны АВ и А₁В₁ не могут пересекаться, ведь они принадлежат параллельным основаниям, поэтому АВ||А₁В₁. Стороны АА₁ и ВВ₁ одинаковы как образующие, при этом прямые АА₁ и ВВ₁ непараллельны, ведь они пересекаются в точке Р. В итоге получается, что АА₁В₁В – равнобедренная трапеция. Отдельно отметим, что ось ОО₁ делит эту равнобедренную трапецию на две прямоугольных трапеции.

Теперь выведем формулы для рассчета площади боковой поверх-ти усеченного конуса. Ясно, что развертка усеченного конуса – это часть развертки поверх-ти исходного конуса:

Нам надо найти площадь фигуры АА₁А₁’А’ (показана желтым цветом). Ее можно найти как разность площадей секторов РАА’и РА₁А₁’. Но эти площади можно вычислить по формуле боковых поверх-тей конусов:

Обозначим длину образующей АА₁ как l. Далее выразим А₁P через r, r₁ и l. ∆АОР и ∆РА₁О₁ подобны, поэтому можно записать:

Подставляем полученное выражение в (1) и получаем:

Чтобы посчитать полную площадь поверх-ти усеченного конуса, необходимо к боковой поверх-ти добавить площади верхнего и нижнего основания:

Рассмотрим несколько задач про конусы.

Задание. Высота конуса составляет 15 см, а его радиус – 8 см. Вычислите длину его образующей.

Решение. Обозначим вершину конуса буквой Р, буквой О – центр основания, а буквой А – произвольную точку на окруж-ти. Тогда высотой конуса будет отрезок ОР, радиусом – отрезок ОА, а образующей окажется отрезок АР:

Высота ОР перпендикулярна плос-ти основания, поэтому ∠РОА – прямой, а ∆РОА – прямоугольный. Тогда АР можно найти по теореме Пифагора:

Задание. Угол между образующей конуса и плос-тью основания составляет 30°, а длина образующей – 12 см. Какова площадь основания конуса?

Решение. Обозначим образующую как АР, а высоту конуса как ОР. Тогда радиус ОА будет проекцией АР на плос-ть основания, то именно ∠РАО будет составлять 30°:

Для вычисления площади основания надо найти радиус АО. Это можно сделать через прямоугольный ∆РОА:

Задание. Осевое сечение конуса имеет площадь 6, а площадь основания равна 8. Вычислите его высоту.

Решение. Пусть осевым сечением будет ∆РАВ, а РО – искомая высота:

Зная площадь основания, легко найдем радиус конуса ОА, а потом и диаметр АВ:

Так как РО – высота для ∆РАВ, то площадь этого треуг-ка может быть рассчитана так:

Задание. Найдите площадь боковой и полной поверх-ти конуса, если образующая имеет длину 8, а радиус основания составляет 5.

Решение. В этой задаче надо просто применить формулу для вычисления площадей:

Задание. Дан конус. Развертка его конической поверх-ти – это сектор, чья дуга составляет 60°. Р – вершина конуса, а РAB – осевое сечение. Вычислите ∠АРВ.

Решение. Длину образующих РА и РВ обозначим как L. Сначала находим длину дуги АА’:

Теперь искомый нами ∠АРВ можно найти с помощью теоремы косинусов, записанной для ∆АРВ:

Задание. Найдите длину образующей усеченного конуса, если радиусы его оснований составляют 6 см и 3 см, а его высота – 4 см.

Решение. Обозначим искомую образующую как АВ, а буквами О и О₁ обозначим центры нижнего и верхнего оснований соответственно:

При изучении осевого сечения усеченного конуса мы уже выяснили, что АВО₁О – прямоугольная трапеция. Опустим в ней высоту ВН, которая будет иметь ту же длину, что и высота конуса ОО₁:

Ответ: 5 см.

Задание. Радиусы оснований усеченного конуса обозначены буквами R и r (R > r). Образующая конуса образует с нижним основанием угол 45°. Составьте формулу, по которой можно найти площадь осевого сечения этого конуса.

Решение. Осевым сечением будет равнобедренная трапеция А₁АВВ₁:

Проведем высоту А₁Н. Вычислим АН:

Теперь площадь трапеции А₁АВВ₁ можно посчитать по формуле:

Задание. Основания усеченного конуса – окружности с радиусами 6 и 7 см. Длина образующей – 5 см. Вычислите площадь его боковой и полной поверх-ти.

Решение. Здесь надо просто подставить данные из условия в формулы для вычисления площадей:

Ответ: 65π см², 150π см².

Сегодня мы узнали две новые объемные фигуры – цилиндр и конус. Эти фигуры иногда называют телами вращения, ведь они получаются вращением плоских фигур вокруг одной из их сторон. Важно помнить, что у всех тел вращения есть такие элементы, как основание (иногда не одно), ось и образующие.

Главная

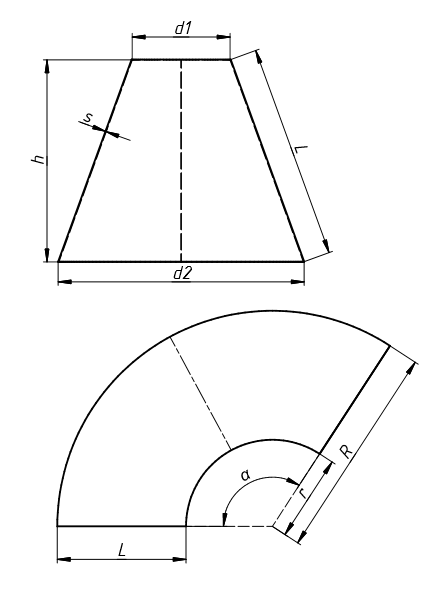
Расчёт параметров усеченного конуса

Параметры усечённого конуса:

Можно использовать для расчета классического конуса — для этого меньший диаметр установить «0». Можно использовать для расчета трубы — оба диаметра выставляются одинаковыми.
Важно d2 должен быть больше d1, иначе углы и радиусы развёртки будут со знаком » — «. В качестве разделителей разряда использовать не запятую, а точку.

d1 — меньший диаметр конуса, мм: , Длина окружности d1, мм:

d2 — больший диаметр конуса, мм: , Длина окружности d2, мм:

h — высота конуса, мм:

s — толщина развёртки, мм:

ρ — плотность материала, кг/м³:

Длина образующей конуса L, мм:

Объём усеченного конуса, мм ³: , м ³: ,
л.

Площадь развёртки усеченного конуса, мм ²: , м ²:

Сумма длин всех сторон развёртки, мм:

Радиус развертки больший R, мм :

Радиус развертки меньший r, мм :

Угол сектора развертки α, ^o :

Масса заготовки из листового материала, кг:

---

---



28.03.2022

На этом уроке мы познакомимся с понятием
усеченного конуса. Дадим определение усеченного конуса. Назовем и рассмотрим
его основные элементы. А затем выведем формулы для вычисления площади боковой поверхности
и площади полной поверхности усеченного конуса.

Итак, рассмотрим понятие усечённого конуса.

Вообще вокруг
нас существует множество предметов, имеющих форму усечённого конуса. Вафельные
стаканчики для мороженного имеют форму усечённого конуса, некоторые стаканы, светильники,
ведра обладают формой очень близкой к форме усечённого конуса.

Некоторые
архитектурные сооружения также имеют форму усечённого конуса. И многое другое.

Возьмём произвольный конус и проведём секущую
плоскость, параллельную его основанию. Эта плоскость пересекается с конусом по кругу
и разбивает конус на две части. Одна из частей (верхняя) представляет собой
конус, а вторая (нижняя) называется усечённым конусом.

Определение:

Усечённым конусом называется
часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной
оси конуса.

Назовём элементы усечённого конуса.

Основание исходного конуса и круг, полученный
в сечении этого конуса плоскостью, называются основаниями усечённого
конуса.

Высотой усечённого конуса
называется отрезок (или его длина), соединяющий центры его оснований.

Прямая  называется его осью.

Часть конической поверхности, ограничивающая
усеченный конус, называется его боковой поверхностью, а отрезки
образующих конической поверхности, расположенные между основаниями, называются образующими
усечённого конуса.

Все образующие усечённого конуса равны друг
другу.

Усечённый конус может быть получен вращением на
 прямоугольной трапеции
вокруг её боковой стороны, перпендикулярной к основаниям.

На экране вы видите усечённый конус,
полученный вращением прямоугольной трапеции  вокруг стороны , перпендикулярной к
основаниям  и . При этом основания усечённого
конуса образуются вращением оснований  и  трапеции, а боковая
поверхность – вращением боковой стороны .

Выведем формулу для вычисления площади
боковой поверхности усечённого конуса.

Для этого нам нужно доказать, что площадь
боковой поверхности усечённого конуса равна , где  и  – радиусы оснований,  – образующая усечённого
конуса.

Доказательство. Пусть  – вершина конуса, из
которого получен усечённый конус,  – одна из образующих
усечённого конуса, а точки  и  – центры его оснований.
Причём, . Тогда площадь боковой
поверхности усечённого конуса равна разности боковых поверхностей двух конусов,
т.е. . Преобразуем это
выражение.

Заметим, что длина образующей  исходного конуса состоит
из суммы отрезков . Используя формулу для
вычисления площади боковой поверхности конуса, получаем: .

Отсюда, учитывая, что , получим следующее
выражение .

Теперь выразим  через ,  и . Прямоугольные
треугольники  подобны
по двум углам. Отсюда следует, что , или .

Значит, получаем, что .

Подставим это выражение в формулу.

Упростим.

В итоге приходим к следующей формуле: .

Этим мы с вами вывели формулу для
вычисления площади боковой поверхности усеченного конуса.

Таким образом, мы доказали, что площадь
боковой поверхности усечённого конуса равна произведению полусуммы длин
окружностей оснований на длину образующей, где  и  – радиусы оснований,  – образующая усечённого
конуса.

Площадью полной поверхности усечённого
конуса называется сумма площадей его боковой поверхности и площади двух
его оснований. Формулу для вычисления площади боковой поверхности усечённого
конуса  мы
с вами вывели выше. Площадь нижнего основания усеченного конуса равна , а площадь меньшего
основания – . Подставим все данные в
формулу.

Отсюда, получаем, что площадь полной
поверхности усеченного конуса можно вычислить по следующей формуле:  .

Теперь давайте решим несколько задач.

Задача: длины радиусов оснований
и образующей усечённого конуса равны соответственно  см,  см и  см. Вычислите его высоту.

Решение: рассмотрим
четырехугольник .

Это есть прямоугольная трапеция с основаниями  и . Высота этой трапеции и
будет высотой нашего усечённого конуса . Для того чтобы её
найти, проведём из точки  меньшего основания
перпендикуляр на большее основание трапеции . Фигура  является
прямоугольником, значит противоположные стороны равны, т.е.  (см), .

Рассмотрим . Он прямоугольный (по
построению). Катет  (см). Применим теорему
Пифагора и найдём длину катета . Получаем, что  (см). Запишем ответ.

Задача: длины радиусов оснований
усечённого конуса равны  см и  см. Вычислите площадь
боковой поверхности этого конуса, если угол между образующей и плоскостью его
основания равен .

Решение: запишем формулу для
вычисления площади боковой поверхности усечённого конуса.

Рассмотрим четырёхугольник .

Это есть прямоугольная трапеция с основаниями  и . Высота этой трапеции и
будет высотой нашего усечённого конуса .

Проведём из точки  меньшего основания
перпендикуляр на большее основание трапеции . Фигура  является
прямоугольником, значит, противоположные стороны равны, т.е.  (см), .

Рассмотрим . Он прямоугольный (по
построению). По условию задачи образующая усечённого конуса наклонена к его
основанию под углом . Следовательно, катет . В свою очередь, . Применим теорему Пифагора
и найдём длину гипотенузы  треугольника . Получаем, что  (см). Значит, образующая
нашего усечённого конуса равна  (см).

Подставим длины радиусов и образующей усечённого
конуса в формулу для вычисления площади боковой поверхности. Посчитаем.
Получим, что площадь боковой поверхности усеченного конуса равна  (см²).

Не забудем записать ответ.

Итоги:

На этом уроке мы познакомились с понятием усечённого
конуса. Узнали, что усечённым конусом называется часть конуса, расположенная
между его основанием и секущей плоскостью, перпендикулярной оси конуса. Назвали
основные элементы усечённого конуса. А также вывели формулы для вычисления
площади боковой поверхности и площади полной поверхности усечённого конуса.

• Площадь и образующая усеченного конуса

  Через площадь оснований усеченного конуса можно найти радиусы оснований, их диаметры, а также периметры данных окружностей, что впоследствии позволит рассчитать высоту, объем и площади поверхности самого конуса.
  r=√(S_r/π)
  R=√(S_R/π)
  d=2√(S_r/π)
  D=2√(S_R/π)
  p=2√(πS_r )
  P=2√(πS_R )

  Трапеция, образованная внутри конуса высотой, образующей и радиусами оснований, является прямоугольной, что позволяет дополнительно построить прямоугольный треугольник из которого можно вычислить высоту через образующую и разность радиусов оснований, а также рассчитать углы при основаниях и образующей.
  h=√(l^2-(R-r)^2 )=√(l^2-(√(S_R )-√(S_r ))^2/π)
  cos⁡β=(R-r)/l=(√(S_R )-√(S_r ))/(l√π)
  α=180°-β

  Площадь боковой поверхности усеченного конуса, выраженная через площади оснований, равна произведению апофемы на сумму квадратных корней из числа π и площадей оснований. Добавив к этому значению непосредственно площади оснований, получим площадь полной поверхности усеченного конуса.
  S_(б.п.)=πl(R+r)=l(√(πS_r )+√(πS_R ))
  S_(п.п.)=S_(б.п.)+S_r+S_R=l(√(πS_r )+√(πS_R ))+S_r+S_R

  Объем усеченного конуса, зная площади оснований и апофему, равен следующему выражению, в котором высота соответствует радикалу, полученному выше по теореме Пифагора.
  V=h/3 (S_r+√(S_r S_R )+S_R )

Пространственные фигуры подробно рассматриваются в старших классах общеобразовательных школ в курсе стереометрии. Данная статья содержит ответ на вопрос о том, как найти образующую конуса круглого прямого и образующую соответствующей усеченной фигуры.

Фигура конус

Чтобы понять, как найти образующую конуса, следует дать представление об этой фигуре. Круглым прямым конусом называют фигуру вращения прямоугольного треугольника вокруг одного из его катетов. Рисунок ниже демонстрирует процесс вращения.

Полученная пространственная фигура имеет следующие характеристики:

1. Сторона AB треугольника является высотой h конуса. Она лежит на оси вращения фигуры.
2. Сторона AC треугольника — это радиус r конуса. Круг, который описывает этот радиус, называется основанием фигуры.
3. Сторона CB треугольника для конуса является его образующей, или генератрисой. Это название она получила за то, что в процессе вращения она описывает коническую поверхность.
4. Вершина B треугольника — это вершина конуса.

Заметим, что высота фигуры пересекает круглое основание в его центре. Это является достаточным условием, чтобы считать конус прямым.

Образующая конуса

Теперь можно переходить к ответу на вопрос о том, как найти образующую конуса круглого прямого. Выше было сказано, что она представляет собой отрезок, который лежит на конической поверхности и соединяет вершину с точкой окружности основания. В прямоугольном треугольнике, из которого был конус получен, образующая является гипотенузой. Это наблюдение позволяет записать известную теорему Пифагора, связав образующую g с радиусом r и высотой h фигуры. Формула, как найти образующую конуса, имеет вид:

g = √(r² + h²)

Помимо этой формулы, на практике вместо высоты или радиуса фигуры может быть известен угол φ между образующей и основанием. В этом случае генератрису g можно рассчитать с помощью следующих выражений:

g = h/sin(φ);

g = r/cos(φ)

Эти формулы следуют из свойств тригонометрических функций синуса и косинуса.

Таким образом, вычисление образующей конуса возможно, если знать любые два параметра фигуры.

Фигура конус усеченный

Он также является фигурой вращения, только вместо прямоугольного треугольника следует вращать прямоугольную трапецию. На рисунке ниже показан усеченный конус.

Здесь синие стрелки показывают прямоугольную трапецию. Длина вертикальной стрелки является высотой h фигуры, длины двух других синих стрелок — это радиусы оснований конуса. В отличие от цилиндра, основания усеченного конуса имеют разную площадь. Обозначим их радиусы r₁ и r₂. Четвертая наклонная к основанию сторона трапеции является образующей или генератрисой. Как и для обычного конуса, для усеченного все генератрисы равны друг другу и образуют боковую поверхность фигуры.

Заметим, что усеченный конус получил такое название потому, что его можно получить не только вращением трапеции, но и с помощью отсечения плоскостью верхней части круглого прямого конуса.

Генератриса усеченной фигуры

Итак, мы познакомились с усеченным конусом, а также с понятием о его образующей. Как находить образующую конуса усеченного? Для того чтобы получить нужную формулу, заметим, если высоту h перенести параллельно самой себе к боковой поверхности конуса так, чтобы она касалась одним концом образующей фигуры, то получится прямоугольный треугольник. Его сторонами будут высота h (катет), генератриса g (гипотенуза) и r₁-r₂ (катет). Тогда можно записать формулу для определения g:

g = √((r₁ — r₂)² + h²)

Соответственно, если дан острый угол φ₁ между большим основанием и генератрисой, тогда последнюю можно определить так:

g = h/sin(φ₁);

g = (r₁ — r₂)/cos(φ₁)

Если же известен тупой угол φ₂ между малым основанием и генератрисой, тогда для ее вычисления необходимо применять такие выражения:

g = h/sin(φ₂);

g = (r₂ — r₁)/cos(φ₂)

Здесь первая формула является точно такой же, как для угла φ₁, а во второй формуле радиусы в числителе поменялись местами.

Таким образом, найти образующую конуса усеченного можно, если знать любые три его параметра.

Просмотры: 24