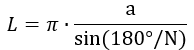8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности — это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
где R — радиус окружности.
2) По диаметру
где D — диаметр окружности.
3) По площади окружности
ггде S — площадь окружности.
4) По диагонали вписанного прямоугольника
где d — диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
где a — сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
где a,b,c — стороны описанного треугольника, S — его площадь.
7) По площади вписанного треугольника
где p — полупериметр вписанного треугольника, S — его площадь.
 По стороне вписанного многогранника
По стороне вписанного многогранника
где a — сторона вписанного многогранника, N — количество сторон.
Скачать все формулы в формате Word
1) Длину окружности приближенно можно найти, умножив её радиус на 6. Начертите окружность радиусом 2 см и найдите длину окружности двумя способами: измерением и вычислением. Сравните результаты.
2) Как можно приближённо вычислить длину окружности, если известен её диаметр?
reshalka.com
Математика 5 класс Дорофеев. 1.4 Окружность. Номер №52
Решение 1
2 * 6 = 12 (см) − длина окружности;
При измерении ниткой длина окружности равна − 12 см 3 мм.
Решение 2
Если известен диаметр окружности, то длину окружности приблизительно можно вычислить умножив диаметр на 3.
Download Article
Download Article
The circumference of a circle is the distance around its edge. If a circle has a circumference of 2 miles (3.2 kilometers), you would have to walk 2 miles (3.2 km) around the circle before you came back to the place you started. When you’re working on a geometric problem, though, you don’t need to leave your seat. Read the problem carefully to find out whether it tells you the circle’s radius (r), diameter (d), or area (A), then find the section that matches your problem. There are also instructions for finding the circumference of an actual circular object you want to measure.
-
1
Draw a «radius» on the circle. Draw a line from the center of the circle to anywhere on the circle’s edge. This line is the «radius» of the circle, often written as just r in math equations and formulas.[1]
- Note: if your math problem doesn’t tell you the length of the radius, you might be looking at the wrong section. Check whether the sections for Diameter or Area make more sense for your problem.
-
2
Draw a «diameter» across the circle.[2]
Extend the line you just drew so it reaches the circle edge on the other side. You’ve just drawn a second radius. The two radii stuck together have a length of «2 x the radius,» written as 2r. The length of this line is the «diameter» of the circle, often written d.Advertisement
-
3
Understand π («pi»).[3]
The π symbol, also written as pi. It isn’t a magical number that just happens to work in this kind of math problem. Actually, the number π was originally «discovered» by measuring circles: if you measure the circumference of any circle (for instance with a tape measure), and then divide by the diameter, you’ll always end up with the same number. This number is unusual because it can’t be written out as a simple fraction or decimal. Instead, we can round to a «close enough» number like 3.14.[4]
- Even the π button on a calculator doesn’t use the exact value of π, although it is close enough.
-
4
Write down the definition of π as an algebra problem. As explained above, π just means «the number you get when you divide the circumference by the diameter.» In the form of a math formula: π = C / d. Since we know the diameter equals 2 x the radius, we can also write this as π = C / 2r.
- C is just a shorter way of writing «circumference.»[5]
- C is just a shorter way of writing «circumference.»[5]
-
5
Change this problem so you are solving for C, circumference. We want to find out what the circumference is, which is C in this math problem. If you multiply both sides by 2r you get π x 2r = (C / 2r) x 2r, which is the same as 2πr = C[6]
- You might have written the left side as π2r, which is also correct. People like to move the numbers in front of the symbols just so the equation is easier to read, and this doesn’t change the result of the equation.
- In a math equation, you can always multiple the left side and the right side by the same amount and still end up with a correct equation.
-
6
Plug in the numbers to solve for C. Now we know that 2πr = C. Look back at the original math problem to see what r (the radius) equals. Then replace π with 3.14, or use a calculator’s π button to get a more accurate answer. Multiply 2πr together using these numbers. The answer you get is the circumference.[7]
- For example, if the radius is 2 units long, then 2πr = 2 x (3.14) x (2 units) = 12.56 units = the circumference.
- In the same example, but using a calculator’s π button for better accuracy, you’ll get 2 x π x 2 units = 12.56637… units but unless instructed otherwise by your teacher, you can round the number to 12.57 units.
Advertisement
-
1
Understand what the «diameter» is. Put your pencil down on the circle’s edge. Draw a line through the center of circle and hitting the edge on the other side. This line is the «diameter» of the circle, often written d in math problems.[8]
- The line goes through the exact center of the circle, not just anywhere within the circle.
- Note: If the word problem doesn’t tell you how long the diameter is, use a different method instead.
-
2
Learn what d = 2r means. The «radius» of the circle, also written as r, is the distance halfway across the circle.[9]
Since the diameter extends all the way across the circle, the diameter is equal to two radii. A simple way to write this is d = 2r. This means you can always replace a d with a 2r in a math problem, or the other way around.- We’ll be using d, not 2r, since your math problem tells you what d equals. However, it’s important to understand this step, so you aren’t confused if your teacher or math book uses 2r where you would expect a d.
-
3
Understand π («pi»).[10]
The π symbol, also written as pi, isn’t a magical number that just happens to work in this kind of math problem. Actually, the number π was originally «discovered» by measuring circles: if you measure the circumference of any circle (for instance with a tape measure), and then divide by the diameter, you’ll always end up with the same number. This number is unusual because it can’t be written out as a simple fraction or decimal. Instead, we can round to a «close enough» number like 3.14.[11]
- Even the π button on a calculator doesn’t use the exact value of π, although it is extremely close.
-
4
Write down the definition of π as an algebra problem. As explained above, π just means «the number you get when you divide the circumference by the diameter.» In the form of a math equation: π = circumference / diameter or π = C / d.
-
5
Change this problem so you are solving for C, circumference. We want to find out what the circumference is, so we need to get C alone on one side. Do this by multiplying each side of the equation by d:
- π x d = (C / d) x d
- πd = C
-
6
Plug in the numbers and solve for C. Look back at the original word problem to see what the diameter equals, and replace the d in this equation with that number. Replace π with an estimate such as 3.14, or use the π button on your calculator for a more accurate result. Multiple the values for π and d together, and you get C, the circumference.[12]
- For example, if the diameter was 6 units long, you’ll get (3.14) x (6 units) = 18.84 units.
- In the same example, but using a calculator’s π button for more accuracy, you’ll get π x 6 units = 18.84956… but unless instructed otherwise, you can round the number to 18.85 units.
Advertisement
-
1
Understand how the area of a circle is calculated. Most of the time, people don’t measure the area (A) of a circle directly. Instead, they measure the radius (r) of the circle, then calculate the area using the formula A = πr2. The reason why this formula makes sense is a little tricky, but you can find out more here if you are interested and willing to tackle some tougher algebra.[13]
- Note: If the math problem does not tell you the area of the circle, you may need to use a different method on this page.
-
2
Learn a formula for calculating the circumference. The circumference (C) is the distance around the circle. Typically, you find it with the formula C=2πr, but because we don’t yet know what the radius (r) is, we’ll have to spend some time figuring out the value of r before we can solve it.[14]
-
3
Use the area formula to get r on one side. Since A = πr2, we can rearrange this formula to solve for r instead. If the steps below are difficult for you to follow, you might want to start on some easier algebra problems or try some techniques for understanding algebra.
- A = πr2
- A / π = πr2 / π = r2
- √(A/π) = √(r2) = r
- r = √(A/π)
-
4
Change the circumference formula using what you found. Any time you have an equation, such as r = √(A/π), you can replace one side of the equation with the other. Let’s use this technique to alter the circumference formula above, C=2πr. For this problem, we don’t know the value of r, but we do know the value of A. Let’s change it like this to make the problem solvable:[15]
- C = 2πr
- C = 2π(√(A/π))
-
5
Plug in the numbers to find the circumference. Use the area given by the problem to solve for the circumference. For instance, if the area (A) of a circle is 15 square units, enter 2π(√(15/π)) into your calculator. Remember to include the parentheses.[16]
- The answer for this example is 13.72937… but unless instructed otherwise you can round to 13.73.
Advertisement
-
1
Use this method to measure real circular objects. You can measure the circumference of circles you find in the real world, not just in word problems. Try it out on a bicycle wheel, a pizza, or a coin.
-
2
Find a piece of string and a ruler. The string must be long enough to wrap around the circle once, and flexible enough that it can wrap tightly. You’ll need something to measure the string with later, such as a ruler or tape measure. The string will be easier to measure if the ruler is longer than the piece of string.
-
3
Wrap the string around the circle once.[17]
Start by placing one end of the string against the edge of the circle. Loop the string around the circle and pull it tight. If you are measuring a coin or other thin object, you might not be able to pull the string tight around it. Lay the circular object flat instead and arrange the string around it, as close to it as you can get.- Be careful not to wrap more than once. You should end up with a single loop of string, so there is no part of the circle with two lengths of string next to it.
-
4
Mark or cut the string. Find the place on the string that completes the loop, touching the end of the string that you started with. Mark this place with a permanent marker, or use a pair of scissors to cut it at this points
-
5
Unravel the string and measure it with a ruler. Take the loop of string and measure it on a ruler. If you used a marker, only measure from the end of the string to the colored mark. This is the part of the string that was wrapped around the circle, and since a circle’s circumference is just the distance around the circle, you’ve found the answer! The length of this string is the same as the circumference of the circle.
Advertisement
Add New Question
-
Question
A bicycle wheel has a radius of 56 cm. How do I calculate the distance the wheel travels in five complete revolutions?
Double the radius. That’s the diameter. Multiply the diameter by pi. That’s the circumference. Multiply the circumference by five. That’s how far the wheel travels in five revolutions.
-
Question
What length of rope would I need to make a one-meter circle?
Assuming the diameter of the circle is to be one meter, multiply the diameter by pi. That means the rope would have to be 3.14 meters long.
-
Question
A semicircle has radius 6 cm. What’s its total perimeter?
The total perimeter is the diameter (twice the radius) plus half the circumference of the full circle. So it’s 12 + (12π / 2) = 12 + 6π = 30.85 cm.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
You can write the plural of radius as either radii or radiuses.[18]
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To work out the circumference of a circle if you know the radius, use the formula 2πr, where π is 3.14 and r is the radius. If you know the diameter instead of the radius, use the formula πd, where d is the diameter, to get the circumference. Know the area of the circle instead? Find its circumference by dividing the area by π, taking that number’s square root, and multiplying it by 2π. To learn how to work out the circumference of a circular object using string and a ruler, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 226,214 times.
Did this article help you?
Вычисление длины окружности
При решении задач и в повседневной жизни можно встретить множество предметов круглой формы, в связи с чем возникает необходимость в их измерении. К примеру, для расчета объема материала, необходимого для производства круглого стакана определенного размера, потребуется построить и найти длину его окружности.
Определение
Окружность представляет собой замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки.
Рассматриваемая в рамках этого определения точка является центром окружности. Если соединить центр с любой точкой, принадлежащей окружности, то получится радиус. Радиусом также называют длину данного отрезка.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус окружности является прямым отрезком, который выходит из центра окружности и проведен до ее границы.
Таким образом, радиус окружности соединяет ее центр с точкой, расположенной на этой окружности. Для обозначения радиуса используют r.
Определение
Диаметр окружности – является прямым отрезком, который соединяет две точки, расположенные на границе окружности, и проходит через центр этой окружности.
Данный параметр обозначают D или d.
Как рассчитать через диаметр или радиус
Длина окружности также является периметром этой окружности. Для расчета длины или периметра круга необходимо знать диаметр или радиус.
Формулы для вычисления длины окружности:
(L = pi DL=pi D)
(L = 2 pi rL=2pi r)
где L – является длиной окружности;
D – определяется, как диаметр окружности;
r – представляет собой радиус окружности;
(pi) – это число Пи, равное примерно 3,14.
Исходя из представленных формул для расчета длины окружности, можно вывести соотношение радиуса и диаметра окружности:
(D = 2rD=2r)
Основные формулы с пояснением
Обладая информацией о радиусе и диаметре окружности, достаточно просто рассчитать ее длину. Однако не во всех задачах присутствуют эти данные. Есть ряд примеров, в которых определить длину окружности необходимо с помощью параметров другой геометрической фигуры.
Вычисление длины окружности через площадь круга
В том случае, когда известна площадь круга, можно рассчитать длину окружности по формуле:
(L=sqrt{S4pi })
где (pi) — является числом пи, значение которого равно 3,14;
S — определяет площадь круга
Расчет длины окружности через диагональ вписанного прямоугольника
В задачах можно встретить примеры вписанного в окружность прямоугольника.
В этом случае длина окружности рассчитывается по формуле:
(L=pi * d)
где ( pi) — является числом пи, значение которого равно 3,14;
d — является диагональю рассматриваемого прямоугольника.
Как вычислить длину окружности через сторону описанного квадрата
В том случае, когда окружность вписана в квадрат с прямыми углами, сторона которого известна, можно определить длину этой окружности.
(L=pi * a)
где (pi ) — является числом пи, значение которого равно 3,14;
a — определяет длину стороны квадрата
Расчет длины окружности с помощью сторон и площади вписанного треугольника
Предположим, что в окружность вписан треугольник. Если имеется информация о всех его трех сторонах, а также площади, то можно рассчитать длину окружности, оперируя следующей формулой:
(L=pi *frac{abc}{2S})
где (pi) — математическая константа со значением 3,14;
a — является первой стороной треугольника;
b — является второй стороной треугольника;
с – является третьей стороной треугольника;
S – определяется, как площадь рассматриваемого треугольника.
Способ нахождения длины окружности при известной площади и полупериметру описанного треугольника
Представим, что в какой-то треугольник вписана окружность. Известно значение площади треугольники и его полупериметр. Необходимо рассчитать длину окружности. Следует заметить, что периметром треугольника называют сумму всех его сторон, а полупериметр составляет половину этой суммы. Таким образом, для нахождения полупериметра нужно определить периметр треугольника и разделить его на два.
Формула расчета длины окружности:
(L=2pi *frac{S}{p})
где (pi) — математическая константа со значением 3,14;
S — является площадью треугольника;
p — представляет собой полупериметр треугольника.
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Когда в окружность вписан правильный многоугольник, в первую очередь стоит сосчитать количество его сторон. Также требуется знать длину стороны этой геометрической фигуры. Стороны правильного многоугольника одинаковы, как у квадрата. В этом случае формула для расчета длины окружности имеет вид:
(L=pi *frac{a}{sin frac({180}{N})})
где (pi) — математическая константа со значением 3,14;
a — это сторона многоугольника;
N — определяет количество сторон многоугольника.
Примеры решения задач
Задача 1
Необходимо рассчитать, какова длина окружности, если ее диаметр составляет 5 см.
Решение
При известном диаметре окружности можно рассчитать ее длину с помощью формулы:
(L = pi D)
Подставив известные из условия задачи значения, получим:
(L = pi D = 3,14 * 5 = 15,7) (см)
Ответ: длина окружности равна 15,7 см.
Задача 2
Требуется определить длину окружности, описанной вокруг правильного треугольника, сторона которого составляет (a=4sqrt{3}) дм.
Решение
Радиус окружности составляет:
(R=frac{a}{sqrt{3}})
При подстановке переменных формула будет изменена:
(R=frac{4sqrt{3}}{sqrt{3}})
При известном радиусе окружности можно рассчитать длину рассматриваемой окружности, используя соответствующую формулу:
(L = 2 pi r=2 pi *4=2*3,14*4=25,12) (дм)
Ответ: длина окружности составляет 25,12 дм.
Задача 3
Дана окружность, радиус которой равен 2 см. Требуется рассчитать длину окружности.
Решение
(L = pi d)
d=2 *r= 4
L = 3.14 * 4 = 12,56 (см)
Ответ: длина окружности равна 12,56 см.
Задача 4
Имеется окружность с радиусом 3 см. Необходимо определить длину данной окружности.
Решение
(L = pi d)
L = 3.14 * 3 = 9,42 (см)
Ответ: длина окружности составляет 9,42 см.

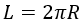
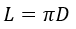
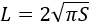
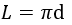
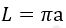
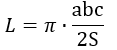
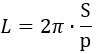
 По стороне вписанного многогранника
По стороне вписанного многогранника