Как найти длину окружности круга 6 класс - Исправление недочетов и поиск решений вместе с Examum.ru

Математика

6 класс

Урок № 76

Длина окружности. Площадь круга

Перечень рассматриваемых вопросов:

окружность, круг и их элементы: радиус, диаметр, хорда;
понятие длины окружности, площади круга;
задачи на вычисление длины окружности и площади круга.

Тезаурус

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которую называют центром окружности.

Круг – это часть плоскости, ограниченная окружностью.

Радиус – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.

Хорда – это отрезок, соединяющий две точки окружности.

Диаметр – это хорда, проходящая через центр окружности.

Длина окружности вычисляется по формулам: С = πd или С = 2πR, где π ≈ 3, 14 – иррациональное число.

Обязательная литература:

Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

Окружность

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которая называется центром окружности.

Элементы окружности: центр, радиус, диаметр.

Отрезок, соединяющий две точки окружности, называется хордой.

Диаметр – это хорда, проходящая через центр окружности.

Ещё в древности было установлено, что какой бы ни была окружность, отношение её длины к её диаметру является постоянным числом. Сейчас это число обозначают греческой буквой π. (читается – «пи»)

Как измерить дину окружности?

Можно взять сантиметровую ленту (если нет ленты, можно воспользоваться нитью или полоской бумаги).

Можно прокатить кольцо по ровной поверхности, сделав полный оборот.

Проверьте, верно ли, что отношение длины окружности к диаметру ≈ 3?

Возьмите несколько круглых предметов (тарелка, стакан, игрушечное колесо и др.).

Результаты измерений можно записать в таблицу в тетради.

Закон для более точного вычисления числа π очень сложен. В настоящее время значение π для точных расчётов в строительстве, авиационной или космической промышленности находят при помощи компьютера.

Вспомните, что π – это иррациональное число, которое выражается бесконечной непериодической дробью.

π = 3,141592653589793238…

При решении обычных задач используют приближенное значение

π ≈ 3,14

иногда используют π ≈ 3

Обозначим длину окружности буквой С, а её диаметр – буквой d, и запишем формулу:

Следовательно, справедливы формулы:

С = πd или С = 2πR

Круг – это часть плоскости, ограниченная окружностью.

С помощью числа π вычисляют площадь круга.

S = πR²

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

Впишите верный ответ.

Радиус круга равен 5 см. Найдите длину окружности С, площадь круга S.

Решение

С = 2πR = 2 ∙ 3,14 ∙ 5 = 31,4 (см).

S = πR² = 3,14 ∙ 5² = 3,14 ∙ 25 = 78,5 (см²).

Ответ: 31,4 см; 78,5 см.

Тип 2. Множественный выбор

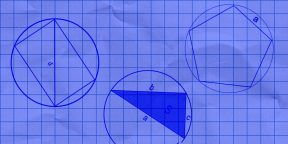
Вычислите площади заштрихованных фигур (размер 1 клетки равен 1 см²).

Варианты ответов

34,24 см²

84,78 см²

50,24 см²

113,04 см²

Фигура 1

Из круга вырезали квадрат.

S_круга = πR² = 3,14 ∙ 4² = 3,14 ∙ 16 = 50,24 (см²).

S_{квадрата} = а² = 4² = 16 (см²).

S_{заштрих} = 50,24 – 16 = 34,24 (см²).

Фигура 2

Из круга вырезали круг.

S₁ = πR² = 3,14 ∙ 6² = 3,14 ∙ 36 = 113,04 (см²).

S₂ = πR² = 3,14 ∙ 3² = 3,14 ∙ 9 = 28,26 (см²).

S_{заштрих} = 113,04 – 28,26 = 84,78 (см²).

Выбираем ответы: 34,24 см² и 84,78 см².

Источник

8 способов найти длину окружности

Выбирайте формулу, ориентируясь на известные величины.

1. Как найти длину окружности через диаметр

Просто умножьте диаметр на число пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d —диаметр окружности.

2. Как найти длину окружности через радиус

Умножьте число пи на два радиуса.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
r — радиус окружности.

3. Как вычислить длину окружности через площадь круга

Умножьте число пи на четыре площади круга.

Найдите корень из результата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
π (пи) — константа, равная 3,14.

4. Как найти длину окружности через диагональ вписанного прямоугольника

Умножьте число пи на диагональ.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
d – любая диагональ прямоугольника.

5. Как вычислить длину окружности через сторону описанного квадрата

Умножьте число пи на сторону квадрата.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
a – любая сторона квадрата.

6. Как найти длину окружности через стороны и площадь вписанного треугольника

Перемножьте стороны треугольника.

Поделите результат на площадь и на два.

Умножьте полученное число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
a, b, c – стороны треугольника.

7. Как найти длину окружности через площадь и полупериметр описанного треугольника

Поделите площадь треугольника на его полупериметр.

Умножьте результат на число пи и на два.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
π (пи) — константа, равная 3,14.
S – площадь треугольника.
p – полупериметр треугольника (равен половине от суммы всех сторон).

8. Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разделите 180 градусов на количество сторон многоугольника.

Найдите синус полученного числа.

Разделите сторону многоугольника на результат.

Умножьте получившееся число на пи.

Иллюстрация: Лайфхакер

O — искомая длина окружности.
a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
π (пи) — константа, равная 3,14.
N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.

Читайте также 📐✏️🎓

Как найти периметр прямоугольника
8 способов найти периметр треугольника
7 способов найти площадь прямоугольника
Как перевести обычную дробь в десятичную
Как освоить устный счёт школьникам и взрослым

Источник

Мы имеем формулу для вычисления длины окружности, если известен диаметр: C = π ⋅ d . Если вспомним, что d = 2 r , то формула длины окружности будет выглядеть так: C = 2 π ⋅ r .

Как найти длину окружности пример?

Если вы нашли радиус, воспользуйтесь формулой C = 2πr, а если диаметр, формулой C = πd.

Пример: найдите длину окружности, радиус которой равен 3 см. Напишите формулу: C = 2πr. Подставьте данное значение в формулу: C = 2π3. …
Пример: найдите длину окружности, диаметр которой равен 9 м. Напишите формулу: C = πd.

Что такое длина окружности 6 класс?

округленное до разряда сотых π ≈ 3,14… Теперь, зная, что такое число π, мы можем записать формулу длины окружности. Длина окружности — это произведение числа π и диаметра окружности. Длина окружности обозначается буквой «С» (читается как «Це»).

Как найти окружность пи?

Формула окружности = Пи x диаметр.

Как решать длину окружности и площадь круга?

Формула вычисления площади круга

S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
S = d2 : 4 × π, где d — это диаметр.
S = L2 : (4 × π), где L — это длина окружности.

23 июл. 2020 г.

Как определить длину окружности и площадь круга?

C = π ⋅ D , или C = 2 π ⋅ R . Так как длина всей окружности равна C = 2 π ⋅ R , то длина дуги в 1° равна 2 π R 360 ° = π R 180 ° . Если градусная мера дуги равна α градусам, то длина такой дуги ∪ AB = l выражается формулой l = π R 180 ° ⋅ α . Площадь круга определяется по формуле S = π ⋅ R 2 .

Как найти площадь и длину окружности?

Формула вычисления площади круга

S = π × r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
S = d2 : 4 × π, где d — это диаметр.
S = L2 : (4 × π), где L — это длина окружности.

23 июл. 2020 г.

Как найти длину?

Чтобы найти длину, надо из периметра вычесть две ширины, так как коротких сторон у прямоугольника две. Остаток надо разделить пополам, потому что длины у прямоугольника тоже две. После этого длину умножить на ширину.

Как называется длина окружности?

Длина окружности (от латинского circumferens) — это длина замкнутой плоской кривой, ограничивающей круг. Поскольку окружность является границей круга, или диска, длина окружности является частным случаем периметра. Периметр — общая длина границы фигуры.

Чем отличается длина окружности от площади круга?

Так как длина всей окружности равна C = 2 π ⋅ R , то длина дуги в 1° равна 2 π R 360 ° = π R 180 ° . Если градусная мера дуги равна α градусам, то длина такой дуги ∪ AB = l выражается формулой l = π R 180 ° ⋅ α . Площадь круга определяется по формуле S = π ⋅ R 2 .

Как определить окружность по диаметру?

Запишите формулу для вычисления длины окружности через диаметр. Формула имеет вид: C = πd, где C — длина окружности, d — диаметр окружности. То есть длина окружности равна произведению диаметра на число π (π примерно равно 3,14).

Как найти диаметр круга 6 класс?

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14. Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

Как найти длину окружности круга?

Для вычисления длины окружности необходимо число Пи умножить на два и умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть следующим образом: 2π · 3√2 = 6√2π дм. Ответ: Длина окружности равна 2π.

Как найти длину окружности и площадь круга 6 класс?

Длина окружности вычисляется по формулам: С = πd или С = 2πR, где π ≈ 3, 14 – иррациональное число….Перечень рассматриваемых вопросов:

окружность, круг и их элементы: радиус, диаметр, хорда;
понятие длины окружности, площади круга;
задачи на вычисление длины окружности и площади круга.

Как измерить длину окружности 5 класс?

Итог урока чему научились сегодня на уроке? (Находить длину любой окружности, зная ее диаметр по формуле: С=π*d.

Как найти площадь половины круга?

Полукруг — это половина круга. Для вычисления площади полукруга необходимо найти площадь полного круга, а затем разделить ее на два.

Какая формула нахождения площади?

S = a × b, где a, b — длина и ширина прямоугольника. S = a × √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.

Источник

Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с
карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность.

Рассмотрим более подробно окружность. Разберёмся, что называют центром,
радиусом и диаметром окружности.

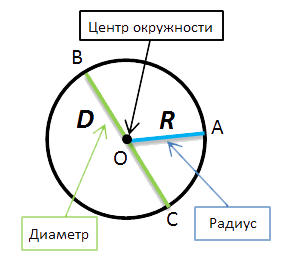
(·)O — называется центром окружности.
Отрезок, который соединяет
центр и любую точку окружности, называется радиусом окружности.
Радиус окружности обозначается буквой «R». На рисунке выше —
это отрезок «OA».
Отрезок, который соединяет
две точки окружности и проходит через её центр, называется
диаметром окружности.

Диаметр окружности обозначается буквой «D».
На рисунке выше — это отрезок «BC».

На рисунке также видно, что диаметр равен двум радиусам. Поэтому
справедливо выражение «D = 2R».

Число π и длина окружности

Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что
такое число π (читается как «Пи»), которое
так часто упоминают на уроках.

В далекие времена математики Древней Греции внимательно изучали окружность
и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.

Запомните!

Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π ≈ 3,14…

Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π,

округленное до разряда сотых
π ≈ 3,14…

Теперь, зная, что такое число π, мы
можем записать формулу длины окружности.

Запомните!

Длина окружности
— это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С» (читается как «Це»).

C = πD
C = 2πR

, так как D = 2R

Как найти длину окружности

Чтобы закрепить полученные знания, решим задачу на окружности.

Разбор примера

Условие задачи:

Найдите длину окружности, радиус которой равен 24 см. Число
π
округлите до сотых.

Воспользуемся формулой длины окружности:

C = 2πR
≈ 2 · 3,14 · 24 ≈ 150,72 см

Разберем обратную задачу, когда мы знаем длину
окружности, а нас просят найти её диаметр.

Разбор примера

Условие задачи:

Определите диаметр окружности, если
её длина равна 56,52 дм.
(π ≈ 3,14).

Выразим из формулы длины окружности диаметр.

C = πD
D = С / π

D = 56,52 / 3,14 = 18 дм

Хорда и дуга окружности

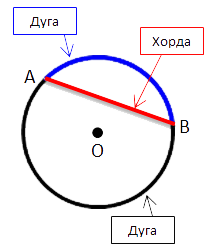
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность
на две части, каждую из которых называют дугой.
Это синяя дуга «AB» и черная дуга «AB».
Точки «A» и «B» называют концами дуг.

Соединим точки «A» и «B» отрезком. Полученный отрезок называют
хордой.

Важно!

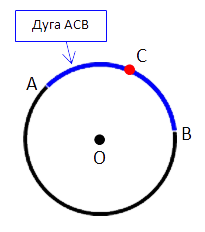
Точки «A» и «B» делят окружность на две дуги. Поэтому важно
понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».

Для того чтобы избежать путаницы, часто вводят дополнительную точку на
нужной дуге и обращаются к ней по трем точкам.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

3 мая 2020 в 10:27

Владислав Заступневич
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Владислав Заступневич
Профиль
Благодарили: 0

Сообщений: 1

, Радиус одной окружности равен 12 см, а второй-36см.Чему равно отношения длины первой окружности к длине второй окружности?

0
Спасибо thanks
Ответить

6 мая 2020 в 15:48
Ответ для Владислав Заступневич

Галина Федотова
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Галина Федотова
Профиль
Благодарили: 0

Сообщений: 3

С=2πR
если длину одной окружности разделить на дилну другой, то 2π сократится, следовательно длины будут относится так же как радиусы, то есть 12:36=

0
Спасибо thanks
Ответить

22 сентября 2016 в 19:03

Вика Камалова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Вика Камалова
Профиль
Благодарили: 0

Сообщений: 2

Помогите 2) чему равен деаметр если радиус равен а)12см б)10 децеметров
1) начертить окружность радиусом а)2 см пот буквой б)4см 5мм (начертиь!)
3)Чему равен радиус если деаметр равен а)6см б)9см в)12м
СРОЧНО СЕГОДНЯ! ПРОШУ!!!

0
Спасибо thanks
Ответить

23 сентября 2016 в 14:51
Ответ для Вика Камалова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Радиус равен половине диаметра. Обратно диаметр равен двум радиусам. Подробнее здесь.
1) а) 12см · 2=24см б)10дм · 2 = 20дм
2) ответил в теме.
3) а) 6см: 2 = 3см б) 9см: 2 = 4см 5 мм в)12м: 2 = 6м

0
Спасибо thanks
Ответить

22 сентября 2016 в 18:54

Вика Камалова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Вика Камалова
Профиль
Благодарили: 0

Сообщений: 2

1)Начертить окружность радиусом а)2 см пот буквой б)4 см 5 мм
cry

0
Спасибо thanks
Ответить

23 сентября 2016 в 14:46
Ответ для Вика Камалова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Радиус окружности это расстояние от центра до любой точки окружности. Подробнее можно посмотреть вот здесь. На линейке циркулем отмеряем необходимый радиус и чертим окружность.

0
Спасибо thanks
Ответить

24 января 2016 в 13:45

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5

Длина окружности и площадь круга.
Я не понимаю как найти площадь круга.

0
Спасибо thanks
Ответить

19 сентября 2016 в 10:56
Ответ для Инна Шабрашина

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

0
Спасибо thanks
Ответить

7 сентября 2015 в 21:08

Игорь Желтоновский
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Игорь Желтоновский
Профиль
Благодарили: 0

Сообщений: 1

радиус — 2,1 м.Найти длинну круга и его площадь(помогите плз)

0
Спасибо thanks
Ответить

2 сентября 2016 в 15:18
Ответ для Игорь Желтоновский

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Длина окружности(l) вычисляется по формуле: l=2?r
Площадь круга(S) вычисляется по формуле: S=?r²Подставляем значения и считаем, приняв ?=3,14
l=2 · 3,14 · 2,1 = 13,188
S = 3,14 · 2,1²=13,8474

Более подробно можно прочитать здесь: math-prosto.ru/index.php?page=pages/circle/square_of_circle.php

0
Спасибо thanks
Ответить

Источник

В ходе очень простого эксперимента можно установить, что какой бы ни была окружность, отношение её длины к диаметру является постоянным числом.

необходима гибкая рулетка для измерения;
несколько разных круглых предметов (тарелки, вазы);
нужно измерить длину окружности вокруг предмета;
надо хотя бы округлённо измерить диаметр окружности;
вычислить округлённое деление длины окружности на длину диаметра окружности (выбрать любое число цифр за запятой).

Конечно, результаты будут немного различаться (измерения очень неточные), но будет заметно, что всегда результат — число около (3).

Если провести более точные измерения, то можно найти более точное значение частного. Это число принято обозначать буквой π (читается как «пи»).
Чаще всего используют приближённое значение числа π

≈

(3.14).
Более точное его значение: π

≈

(3,1415926535897932).

Но цифр за запятой намного больше, это бесконечная десятичная непериодическая дробь. Благодаря развитию вычислительной техники совсем недавно стало возможно распечатать довольно много цифр числа π.

Мы имеем формулу для вычисления длины окружности, если известен диаметр:

C=π⋅d

Если вспомним, что

d=2r

, то формула длины окружности будет выглядеть так:

C=2π⋅r

Как же вычислить площадь круга? Один из подходов для определения формулы:

представим, что круг разделён на половины, и каждая из половин поделена на равные части (на рисунке ниже):

Рис. (1). Круг, делённый на равные части

Из частей сложим прямоугольник со сторонами (r) и π(r).

Рис. (2). Прямоугольник, сложенный из частей круга

Для получения более точного результата можно бесконечно уменьшать количество частей круга, чтобы сложенная фигура была как можно больше похожа на прямоугольник.

Видим, что площадь круга вычисляется по формуле

S=π⋅r2

Источники:

Источник