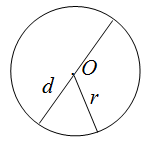Найдите длину окружности, описанной около квадрата со стороной 8 см.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,937
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
http://matworld.ru/geometry/kvadrat.php
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
или
Из равенства (1) найдем d:
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
или
Из формулы (5) найдем R:
или, умножая числитель и знаменатель на 
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Смотрите также:
- Площадь квадрата онлайн
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около квадрата. Также разберем примеры решения задач для закрепления изложенного материала.
-
Формулы вычисления радиуса описанной окружности
- Через сторону квадрата
- Через диагональ квадрата
- Примеры задач
Формулы вычисления радиуса описанной окружности
Через сторону квадрата
Радиус R окружности, описанной около квадрата, равняется длине его стороны a, умноженной на квадратный корень из двух и деленной на два.
Через диагональ квадрата
Радиус R описанной вокруг квадрата окружности равен половине его диагонали d.
Примеры задач
Задание 1
Длина стороны квадрата равняется 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Применим первую формулу, рассмотренную выше:
Задание 2
Вычислите длину диагонали квадрата, если радиус описанной вокруг него окружности составляет 6 см.
Решение
Как мы знаем, радиус описанной окружности равняется половине диагонали квадрата. Следовательно, общая длина диагонали равняется 12 см (6 см ⋅ 2).
Содержание:
- Формула
- Примеры вычисления длины окружности
Формула
Чтобы найти длину окружности, нужно либо диаметр окружности умножить на
$pi approx 3,1415926535 dots$, либо найти удвоенное произведение радиуса и числа
$pi$.
То есть нужно воспользоваться одной из формул:
$l=2 pi r text { или } l=pi d$
Здесь $r$ — это радиус заданной окружности,
а $d$ — диаметр,
$pi approx 3,1415926535 dots$. Радиусом окружности — отрезок, который соединяет центр
окружности с точкой окружности. Диаметром называют отрезок, который соединяет две точки окружности и проходит через её центр. Число
$pi$ — математическая константа , выражающая
отношение длины окружности к длине её диаметра.
Примеры вычисления длины окружности
Пример
Задание. Найти длину окружности, диаметр которой равен 3 см.
Решение. Для вычисления длины заданной окружности воспользуемся формулой
$$l=pi d$$
Подставляя в неё исходные данные, получим:
$l=3 pi approx 3.14 cdot 3=9.42$ (см)
Ответ. $l=3 pi approx 9.42$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти длину окружности, описанной около правильного треугольника со стороною
$a=4 sqrt{3}$ дм.
Решение. Радиус окружности, описанной около правильного треугольника, равен
$R=frac{a}{sqrt{3}}$. В нашем случае он будет равен
$R=frac{4 sqrt{3}}{sqrt{3}}=4$ (дм)
Для нахождения длины рассматриваемой окружности воспользуемся формулой
$l=2 pi r$
Подставляя в нее найденное значение радиуса и значение
$pi approx 3.14 ldots$, окончательно получим
$l=2 cdot pi cdot 4 approx 8 cdot 3,14=25,12$ (дм)
Ответ. $l=8 pi approx 25,12$ (дм)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно вычислить длину окружности при условии, что площадь
круга (S) является известной величиной?
Площадь круга (S) рассчитывается путем умножения числа Пи на длину его
радиуса (R), возведенную в квадратную степень (S = ПR²). Из указанного
равенства можно выразить радиус:
R² = S/ П
Если избавиться от квадратной степени, то получится:
R = √(S/П)
Длина окружности (L) рассчитывается путем умножения числа Пи на длину
радиуса, и последующего умножения на два полученного в результате числа:
L = 2ПR
Если R = √(S/П), то L = 2П*√(S/П)
Каким образом можно найти длину окружности, диаметр которой составляет 2 см?
Длина окружности (L) представляет собой число, которое получено в
результате умножения числа Пи на диаметр данной окружности:
L = П*D
В конкретном случае:
L = 3,14*2 = 6,28 см.
Ответ: Длина окружности с диаметром 2 см составляет 6,28 см.
Дан квадрат, вокруг которого описана окружность. Ее длина составляет 12 Пи
см. Как можно найти длину окружности, вписанной в этот же квадрат?
Известно, что длина окружности (L) рассчитывается путем умножения на два
произведения числа Пи и длины ее радиуса (R). Формула выглядит так:
2ПиR
Из данной формулы можно выразить радиус
R = 12пи/2пи = 6 см
Радиус окружности, описанной около квадрата, равен 6 см.
Теперь можно вычислить сторону квадрата, вокруг которого описана данная
окружность. Ее длина составляет R корней из 2:
а = 6 корней из 2.
Рассчитываем длину малого радиуса (r), который равен половине длины
стороны квадрата:
r = а/2 = 6 корней из 2/2 = 3 корней из 2.
Длина окружности, вписанной в квадрат, рассчитывается по той же формуле:
L = 6 корней из 2 Пи.
Каким образом можно вычислить длину окружности, а также найти ее площадь,
при условии, что радиус этой окружности равен 30 см?
Радиус окружности, равный 30 см, обозначается как R.
Площадь окружности можно найти, умножив число Пи на квадрат длины ее
радиуса:
S = πR²
Подставим в формулу известные величины:
S = π*30² = 900π см. кв.
Длина окружности обозначается как С и рассчитывается путем умножения на 2
произведения числа Пи и ее радиуса:
C = 2πR
Снова подставляем в формулу величины, которые известны:
C = 2π*30 = 60π см
Ответ: Площадь окружности равна 900π см², а ее длина составляет 60π см.
Дана окружность, в которую вписан правильный треугольник. Его площадь
составляет 12√3 см кв. Как можно вычислить длину окружности в данном случае?
По условию задачи известно, что треугольник является правильным, что
означает равенство всех его трех сторон. В данном случае его площадь может
быть рассчитана по следующей формуле:
S = а^2 * √3 ÷ 4
Зная площадь, мы получаем возможность вычислить длину стороны а. Она будет
равна ± √48. Учитывая то, что сторона не может быть отрицательной
величиной, можно говорить о том, что сторона а равна √48.
После того как длина стороны стала известна, можно приступить к вычислению
площади описанной и вписанной окружности. Для этого не достает еще одного
элемента – длины радиуса.
Радиус описанной окружности (R) равен длине стороны треугольника,
разделенной на √3:
R = √48 ÷ √3 = 4 см.
Радиус вписанной окружности (r) можно получить, разделив на 2 радиус
описанной окружности:
r = 4/2 = 2 см.
Вычисленные длины радиусов вписанной и описанной окружностей позволяют
определить ее длину ℓ, которая равна произведению числа Пи и радиуса
окружности, умноженному на 2:
ℓ = 2πR
В нашем случае длина описанной окружности рассчитывается как:
ℓ= 2πR = 2π4 = 8π
Длина вписанной окружности будет составлять:
ℓ= 2πR = 2π2 = 4π
Известно, что радиус окружности равен 12 см. Как вычислить ее площадь и
длину при Пи=3,14?
В условии задачи говорится о том, что радиус окружности R равен 12 см. Ее
длина может быть вычислена посредством умножения на 2 произведения длины
радиуса и числа Пи:
C=2πR
Известно, что число Пи – это константа, равная 3,14. Тогда длина
окружности (С)высчитывается следующим образом:
C=2*3*12=72 см
Площадь окружности можно найти, умножив число Пи на длину ее радиуса,
возведенную в квадратную степень:
S=πR²=3,14*12²=3,14*144=452,16 см кв.
Как можно вычислить радиус окружности и ее диаметр, если известно, что ее
длина составляет 20 Пи см?
По условию задачи длина окружности равна 20 Пи см. Зная формулу, по
которой вычисляется длина окружности, можно записать следующее равенство:
2Пи = 2ПиR
Можно сократить Пи в обеих частях записанного равенства, в результате чего
получится, что:
2R = 20
Теперь высчитаем, чему равна длина радиуса окружности:
R = 20/2 = 10 см.
Длина диаметра равна длине радиуса, умноженной на 2:
D = R*2 = 10*2 = 20 cм.
Длина дуги окружности составляет 6Пи см, при этом ее градусная мера равна
120 градусов. Каким образом можно вычислить радиус окружности?
Полная градусная мера любой окружности равна 360 градусов. В случае,
описанном в задании, градусная мера окружности составляет 120 градусов,
что равно 1/3 части 360 градусов. Это позволяет сделать вывод о том, что
длина окружности (L) может быть рассчитана следующим образом:
L = 6Пи * 3 = 18Пи
Формула, по которой вычисляется длина окружности, выглядит так:
L =2пR
Из данной формулы можно выразить радиус (R):
R = L/2Пи
В заданном случае длина радиуса будет равна:
18Пи/2Пи = 9 см.
Как на радиус окружности повлияет увеличение ее длины на 9,42 см?
Обозначим прежнюю длину окружности как L, а новую – как L₁. Тогда можно
записать следующее равенство:
L₁ — L = 9,42 см
Прежний радиус окружности примем за R, а новый ее радиус, который
получится в результате увеличения длины, обозначим как R₁. Для того чтобы
вычислить ее значение, следует сначала записать формулу, по которой
вычисляется прежняя длина данной окружности:
L = 2πR
Тогда формула для вычисления новой длины окружности будет иметь такой вид:
L + 9,42 = 2πR₁
Отнимем от новой длины старую, и в итоге получим:
2πR₁ — 2πR = 9,42 см.
Перенесем 2Пи из левой части равенства в правую:
R₁ — R = 9,42 : 2π = 1,5 см.
Ответ: В результате увеличения длины окружности на 9,42 см ее радиус
станет больше на 1,5 см.
Как можно вычислить радиус окружности, вписанной в правильный треугольник,
зная то, что площадь данного треугольника превышает площадь окружности на
27√3-9π?
Радиус окружности, которая вписана в правильный треугольник, обозначим r.
Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:
S = πr²
В случае треугольника, все стороны которого одинаковы, радиус вписанной в
него окружности равен третьей части высоты, являющейся также и медианой.
Площадь правильного треугольника рассчитывается так:
Sтр = (1/2)*(2r/tg30)*3r = (1/2)*(2r√3)*3r = 3√3r².
Согласно условию задачи 3√3r² = πr² + 27√3 — 9π.
Перенесем πr² из левой части равенства в правую, изменив его знак на
противоположный:
3√3r² — πr² = 27√3 — 9π
Вынесем в правой части равенства r² за скобки. То же самое сделаем с
числом 9 в левой части равенства:
r²(3√3 — π) = 9(3√3 — π)
Сокращаем в обеих частях одинаковый множитель (3√3 — π) и получаем:
r² = 9
Таким образом, радиус окружности равен корню квадратному из 9:
r =3 см.
Дано две окружности, радиус одной из которых пятикратно превышает радиус
другой. Каким образом вычислить радиус каждой из этих окружностей, если
известно, что диаметр второй из окружностей на 240 мм меньше, чем диаметр
первой?
Обозначим радиус второй окружности буквой х. В данном случае радиус первой
окружности нужно обозначить как 5х. Известно, что разница между длинами
диаметров двух окружностей равна 240 мм. На основании этого можно
составить следующее равенство:
5х-х=240:2, что равно 4х=120
Теперь можно найти значение х:
х=120:4=30 мм.
Таким образом, радиус второй окружности равен 30 мм. Это позволяет
вычислить радиус первой окружности, который в 5 раз больше радиуса второй
из них:
30*5=150 мм.
Как можно высчитать радиус окружности, когда известна ее градусная мера и
длина дуги?
Длина дуги обозначена как L. В качестве обозначения ее градусной меры
используется α. Через R обозначена длина радиуса данной окружности.
Формула расчета длины дуги выглядит так:
L = πR · α / 180°
Это же равенство может быть переписано следующим образом:
πR · α = L · 180°
Отсюда выведем радиус:
R = L · 180° / (π·α).
Как высчитать радиус окружности, длина дуги которой составляет 3,14 см, а ее
градусная мера равна 18 градусам?
Длина окружности (L) равна произведению числа Пи и радиуса, которое
умножено на 2:
L = 2Пиr
Согласно заданию, длина дуги равна 3,14, что равно значению константы Пи.
Дуга способна поместиться в длине окружности 2 пи r/пи =2 r раз
Подставив в равенство значения, которые известны, мы получим:
360:18=20 раз
Длина окружности будет равна:
3,14*20=20Пи
2Пиr = 20Пи
Сократим 2Пи в каждой из частей равенства и получим, что:
r=10 см.
Площадь круга составляет 169Пи см. Чему равна длина окружности в данном
случае?
Для решения поставленной задачи следует записать формулу расчета площади
круга:
S=πr2
Эта величина указана в задании, и составляет 169Пи. Это значит, что:
πr2 = 169π
Можно сократить одинаковый множитель Пи в обеих частях равенства:
r2= 169
r = √169 = 13 см.
Длина окружности обозначена С. Она считается по следующей формуле:
С = 2πr
Длина радиуса уже известна, и ее можно подставить в формулу расчета длины
окружности:
С = 2* π*13 = 26π см.
В окружность вписан квадрат площадью 36 дм кв. Чему в этом случае будет
равна площадь круга и длина окружности?
Известно, что площадь круга представляет собой величину, равную длине
стороны этого квадрата, возведенной во вторую степень Sкв = а². Это
значит, что в данном случае а² = 36 дм. Для того чтобы найти значение а,
нужно извлечь квадратный корень из 36:
а = √36 = 6 дм.
Длина диагонали (d) квадрата считается по приведенной ниже формуле:
d = a√2 = 6√2 дм.
Радиус (R)окружности, которая описана около квадрата, равен половине длины
ее диагонали:
R = d/2 = 3√2 дм.
Площадь круга можно посчитать, умножив число Пи на квадрат его радиуса:
S = πR² = π · (3√2)² = 18π дм. кв.
Длина окружности рассчитывается посредством умножения на два числа Пи,
после чего полученное число умножается на длину радиуса окружности:
C = 2πR = 2π · 3√2 = 6√2π дм.
Длина окружности составляет 3,5 дм. Диаметр второй окружности равен 5/7 ее
диаметра. Как вычислить длину второй окружности?
Ниже записана формула, которая используется для того, чтобы рассчитать
длину окружности:
С = Пи*d,
где Пи – это константа, равная 3,14, а d – это диаметр окружности.
Отношение длины первой окружности к длине второй окружности равно
отношению их диаметров:
C/C1 = d/d1
d1 = 5/7 d
В условии сказано, что длина первой окружности С = 3,5 дм. Таким образом:
C1 = 5/7 *C = 5/7 * 3,5 = 2,5 дм.
Длина радиуса окружности составляет 14 см. Какова будет ее длина при
условии, что П=22/7?
Для того чтобы узнать длину окружности (C), следует воспользоваться
формулой, предназначенной для ее расчета. Она выглядит так:
C = П*R*2
Если подставить в эту формулу величины, которые даны по условию задачи, то
получим:
22/7*14*2=22/7*28/1=88 см.
Ответ: Длина окружности равна 88 см.
Какой будет длина окружности при условии, что ее половина составляет 25,5
см?
Длина окружности равна длине ее половины, умноженной на 2. Это значит, что
в данном случае нужно умножить число 25,5, обозначающее половину длины
окружности, на 2:
25,5*2 = 51 см.
Круг имеет площадь Пи м кв. Какова будет длина окружности данного круга?
Для вычисления длины окружности необходимо число Пи умножить на два и
умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть
следующим образом:
2π · 3√2 = 6√2π дм.
Для того чтобы посчитать площадь круга, необходимо умножить число Пи на
радиус, взятый в квадрат (S = πR²). По условию задачи площадь круга равна
Пи м кв. Это значит, что:
πR² = π
Из данного равенства можно выразить R
R — √π/π = 1
Зная длину радиуса, можно переходить к вычислению длины окружности (С):
C = 2πR = 2π x 1 = 2π
Ответ: Длина окружности равна 2π.
Какова формула длины окружности, при условии, что длина ее радиуса
составляет R?
С целью вычисления длины окружности (С) используется приведенная ниже
формула:
C=2πR
Ее составляющими является постоянное число Пи и радиус окружности (R),
длину которой необходимо вычислить.
Какова формула расчета длины окружности, диаметр которой составляет 15 см?
Если длина диаметра окружности является известной величиной, то его нужно
умножить на постоянное число Пи, равное 3,14, для того чтобы найти длину
этой окружности. Формула выглядит так:
С = πD
В условии говорится, что диаметр окружности равен 15 см:
С = 3,14 * 15 = 47,1 cм.
Ответ: Длина окружности равна 47,1 см.
В результате деления длины окружности на величину ее диаметра получается
число, приблизительно равное 22/7. Каким образом можно высчитать длину
окружности с диаметром 10 см?
Для расчета длины окружности (С) нужно знать длину ее радиуса (R) или
диаметра (d). Тогда могут быть использованы следующие формулы:
C = 2πR или C = πd
По условию задания d = 10 см, а π = 22/7. Тогда длина окружности будет
равна:
C = πd = (22/7) * 10 = 220/7 ≈ 31,4 см.
В каком виде представлены формулы, которые используются для вычисления
площади круга и длины окружности (через диаметр и через радиус)?
В случае, если длина диаметра (d) или длина радиуса (R) окружности
известны, то эти величины можно использовать для нахождения длины
окружности. При этом следует воспользоваться одной из формул:
С=πd или С=2πR.
Эти величины также помогут вычислить площадь круга. Формулы выглядят
следующим образом:
S=πr² или S=π(d2)².
Можно ли вычислить длину диаметра окружности, если известна только ее длина?
Нужно записать формулу расчета длины окружности, для того чтобы понять,
существует ли взаимосвязь между этой величиной и диаметром окружности:
L = π·d
Очевидно, что длина окружности является результатом умножения числа Пи на
длину ее диаметра.
Если длина окружности известна, то ее можно использовать для определения
диаметра (d). Это можно сделать следующим образом:
d = L/π.
Во сколько раз длина окружности превышает ее диаметр, и в каком виде
представлена формула ее расчета через диаметр?
Длину окружности (С) можно рассчитать через диаметр (d), если
воспользоваться нижеприведенной формулой:
С = π*d
Это формула демонстрирует, что длина окружности больше длины ее диаметра в
π раз. Именно отношение длины окружности к величине ее диаметра и является
числом π.
Какова формула вычисления отношения длины окружности к величине, означающей
ее диаметр?
Число π представляет собой константу, которая получается в результате
деления длины окружности (С) на ее диаметр (d). В виде формулы это
выглядит так:
π = С/d
Площадь круга составляет 185 см кв. Как вычислить 30% от длины окружности
при заданных исходных?
Располагая информацией о том, что площадь круга равна произведению числа
Пи и квадрата ее радиуса (S=πr²), можно через нее выразить радиус:
r² = S/π = 185/π
Избавляемся от квадратной степени:
r = √(185/π) см.
Следующим шагом в решении задачи станет вычисление длины окружности,
которая находится путем умножения на 2 числа Пи и радиуса окружности:
С=2πr= C=2π√(185/π) = 2√(185π) см.
На последнем этапе находим 30%. Принимаем всю длину окружности за 100%:
2√(185π) — 100%
х — 30%
Тогда х можно найти следующим образом:
х=(30*2√(185π))/100 = 0,6√(185π) см.
Как выглядят формулы определения длины окружности через радиус и через
диаметр? В какое количество раз длина диаметра окружности меньше ее длины?
Существует две формулы, которые предназначены для расчета длины окружности
(С). Они отличаются друг от друга тем, что элементом одной из них является
радиус (r), а другой – диаметр (D):
C=2Пr и C=ПD.
Для того чтобы понять, во сколько раз длина окружности превышает длину ее
диаметра, нужно произвести деление этих величин:
С/D
В результате получается число Пи, которое является постоянным и имеет
значение примерно 3,14.
Длина окружности, обозначаемая как L, может быть вычислена при условии, что
известен ее диаметр (D). При этом следует воспользоваться формулой L = Пи*D.
Можно ли использовать данную формулу с целью вычисления длины диаметра
окружности, длина которой составляет 126 м. (число Пи считать равным 3)?
Формула расчета длины окружности (С) через диаметр (D) выглядит так:
С = Пи*D
Исходя из условий задания, это равенство может быть записано в следующем
виде:
126=3*D
Отсюда можно выразить диаметр:
D=126:3=42 м.
Читать дальше: как найти периметр квадрата.
Окружность вписанная в квадрат
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. 
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.
Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:
Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.
Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: 
Окружность описанная около квадрата

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:
- угол CDA=90°;
- стороны AD=CD. Признак равнобедренного треугольника;
- угол DAC равен ACD. Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:

Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна 

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
Рассмотрим пример
Задача
: радиус окружности вписанной в квадрат равен 
Дано
:
- треугольник ОСЕ – равнобедренный и прямоугольный;
- ОЕ=ЕС=
;
- ОЕС=90°;
- ЕОС=ОСЕ=45°;
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.