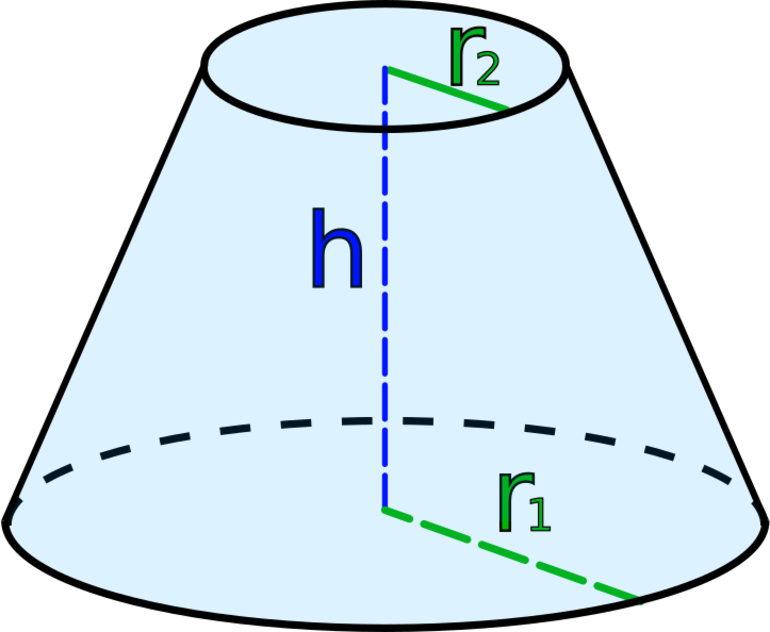
Радиус и высота усеченного конуса
Свойства
Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса. d=2r D=2R p=2πr P=2πR S_r=πr^2 S_R=πR^2
Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения l=√(h^2+(R-r)^2 ) tanβ=h/(R-r) α=180°-β
Площадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса. S_(б.п.)=πl(R+r) S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2
Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета. V=πh/3(R^2+rR+r^2)
Усеченный конус — построение фигуры, формулы и задачи
Исходный полный конус
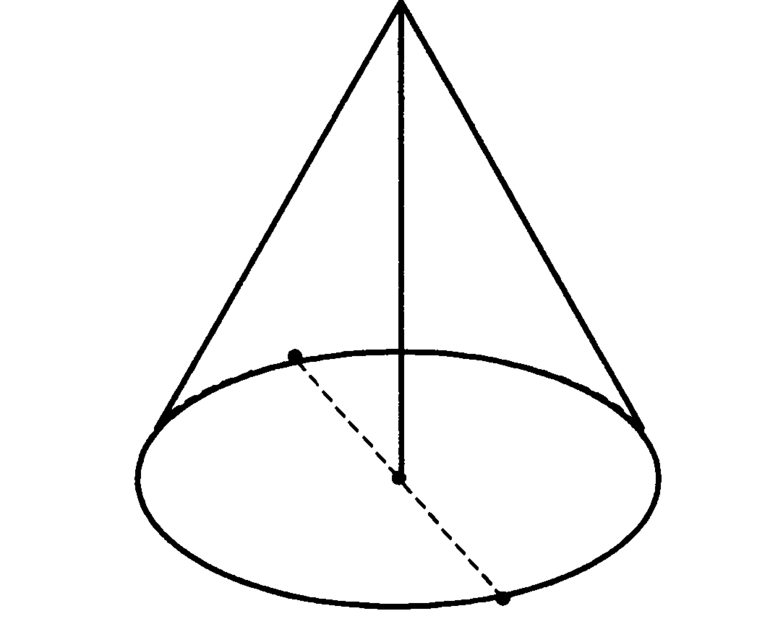
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
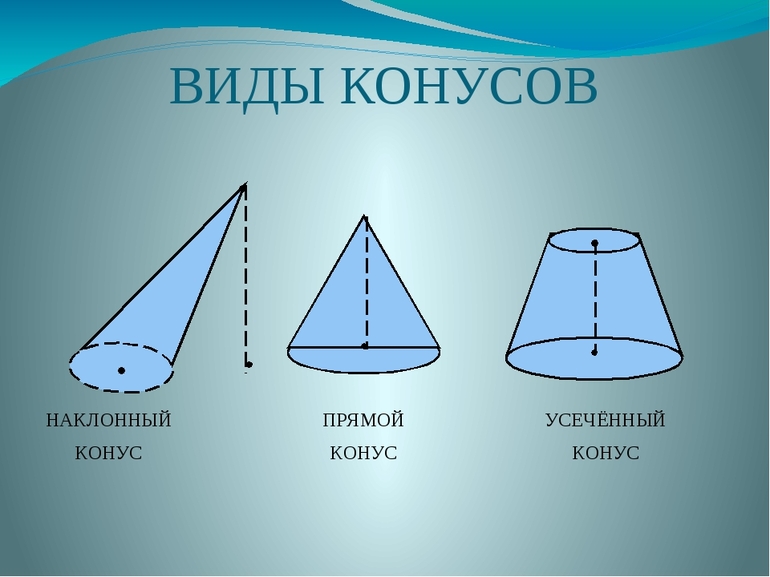
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r 2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r 2 *h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r 2 . Для боковой поверхности следует выполнить следующие действия:
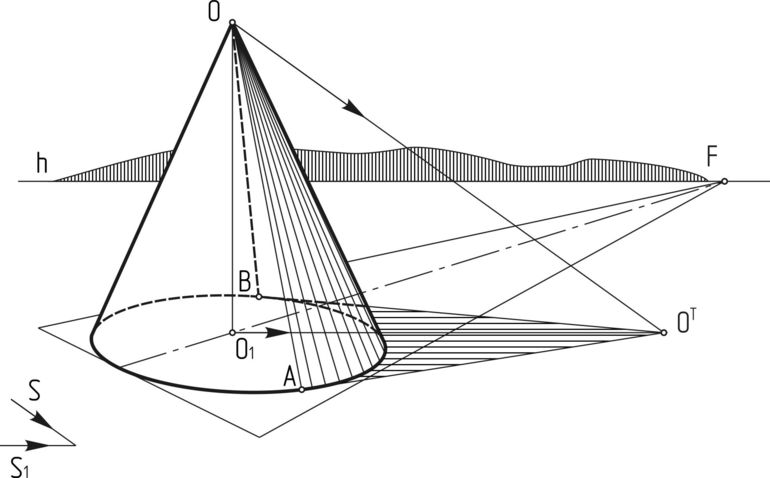
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r1 2 + pi*r2 2 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r1 2 *H — 1/3*pi*r2 2 *(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r1 2 + r2 2 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см 2 . При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r1 2 + pi*r2 2 = 4*pi*r2 2 + pi*r2 2 = 5*pi*r2 2 .
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h 2 )^0,5 = (2,52 2 + 15 2 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см 2 .
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
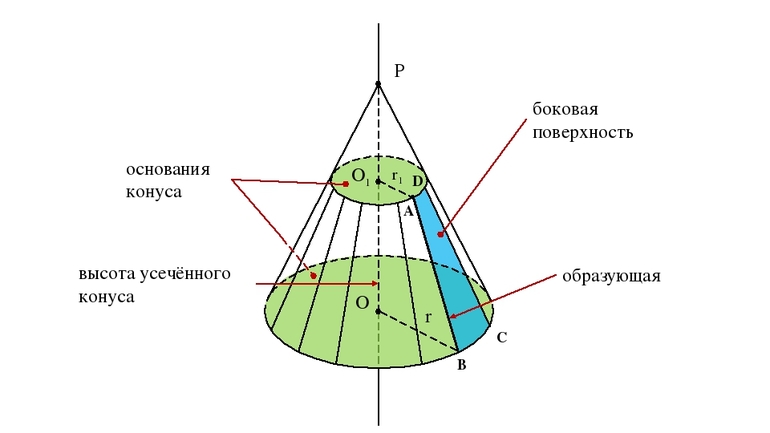
Что такое усеченный конус: определение, основные элементы
В данной публикации мы рассмотрим определение и основные элементы усеченного конуса. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение усеченного конуса
Усеченный конус (конический слой) – это геометрическая фигура в пространстве; часть конуса, оставшаяся между его основанием и секущей плоскостью, параллельной этому основанию.
Примечание: В рамках данной публикации мы будем рассматривать самый распространенный вид усеченного конуса – прямой круговой.
Усеченный конус образуется путем вращения на 360° прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию, или равнобедренной трапеции вокруг своей оси симметрии на 180°.
На рисунке ниже конус образован путем вращения равнобедренной трапеции ABCD вокруг оси O1O2.
Основные элементы усеченного конуса
- R – радиус бОльшего основания конуса, являющегося кругом, с центром в точке O1 и диаметром AD.
- r – радиус меньшего основания конуса с центром в точке O2, диаметр – отрезок BC.
- h (O1O2) – высота конуса; одновременно является высотой трапеции ABCD и осью симметрии обеих фигур.
Развёртка боковой поверхности усеченного конуса выглядит следующим образом:
Длина бОльшей (меньшей) дуги равна длине окружности соответствующего основания конуса ( 2πR или 2πr ).
http://nauka.club/matematika/geometriya/usechennyy-konus.html
Исходный полный конус
Прежде чем говорить об усеченном объекте и его характеристиках, следует рассмотреть исходную фигуру, из которой он получается.
Пусть имеется некоторая замкнутая кривая, лежащая в произвольной плоскости. Это может быть окружность, эллипс или любая другая линия с плавными перегибами. Пусть также существует отрезок, который не лежит в плоскости указанной замкнутой кривой. Если в пространстве зафиксировать некоторую точку, а затем соединить ее с любой точкой на кривой, то получится образующая будущего конуса. Если теперь ее перемещать вдоль замкнутой кривой одним своим концом, в то время как другой конец будет зафиксированным в точке, то она опишет коническую поверхность.
Это геометрическое построение позволяет получить объемную фигуру конус, которая состоит из следующих элементов:
- Вершина — зафиксированная точка в пространстве, которая не лежит в плоскости замкнутой кривой.
- Коническая поверхность, образованная в результате перемещения отрезка — образующей, или генератрисы.
- Основание — часть плоскости, ограниченная исходной замкнутой кривой. Последняя является направляющей, или директрисой, для образующей.
Существующие виды
В геометрии известны несколько видов конуса. Каждый из них определяется характером директрисы и расположением относительно нее генератрисы. Выделяют следующие виды фигуры:
- Круглый прямой. В его основании лежит круг, а высота (длина перпендикуляра, опущенного из вершины) соединяет центр окружности и вершину.
- Эллиптический прямой. В его основании находится эллипс, а проекция вершины попадает точно в центр основания.
- Наклонный произвольного вида. Высота в этом конусе всегда меньше, чем длина отрезка, соединяющего вершину и геометрический центр основания.
Круглая прямая фигура
Получить этот конус несложно. Необходимо взять прямоугольный треугольник, поставить его на один из катетов и вращать вокруг второго катета, который будет являться осью, а его длина — высотой для объемной фигуры. Катет, на котором стоит треугольник, является радиусом круглого основания конуса.
С полученной фигурой легко работать при решении геометрических задач, поскольку для нее существуют довольно простые формулы для площади поверхности и объема.
Площадь S фигуры состоит из двух частей: основания и боковой поверхности. С помощью простых геометрических рассуждений можно показать, что сумма этих частей выражается в виде такой формулы: S = pi*r2 + pi*g*r, где число pi=3,14, r — радиус окружности в основании, g — длина генератрисы. В разрезе на плоскости коническая поверхность представляет собой сектор круга радиусом g.
Объем рассматриваемого конуса выражается следующей формулой: V = 1/3*pi*r2*h. Здесь h — высота фигуры. Можно заметить, что величина V ровно в три раза меньше аналогичной для цилиндра, имеющего то же основание, что и конус. Записанную формулу может вывести любой школьник, который знаком с интегральными вычислениями.
Усеченный геометрический объект
Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.
Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.
Способы построения
Можно выделить два основных способа построения усеченного круглого геометрического объекта:
- из круглого прямого конуса;
- с помощью трапеции.
В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной. Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.
Второй способ получения усеченного конического объекта связан с использованием фигуры трапеции прямоугольного типа. Такая трапеция представляет собой два параллельных отрезка, которые имеют длины a и b. Они соединены одним перпендикуляром h и косым отрезком g.
Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.
Площадь поверхности
Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:
- Разрезать ее вдоль образующей и развернуть на плоскости.
- Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
- Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
- Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую. В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).
Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:
S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).
Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.
Формула объема
Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:
V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).
Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:
V = 1/3*pi*h*(r12 + r22 + r1*r2).
Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:
V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).
Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.
Пример решения задачи
Известно, что сумма площадей двух оснований усеченного прямого круглого конуса составляет 100 см2. При этом радиус большего основания в 2 раза превышает радиус меньшего. Необходимо найти площадь боковой поверхности фигуры, высота которой составляет 15 см.
Из данных задачи можно определить значение каждого радиуса. Для этого необходимо ввести следующее равенство: r1 = 2*r2. Тогда для суммы площадей оснований можно записать выражение:
S = S1 + S2 = pi*r12 + pi*r22 = 4*pi*r22 + pi*r22 = 5*pi*r22.
Откуда получается:
r2 = (S/(5*pi))^0,5 = (100/(5*3,14))^0,5 = 2,52 см.
Тогда радиус большего основания будет равен r1 = 2*r2 = 5,04 см.
Чтобы найти генератрису g усеченного конуса, следует рассмотреть прямоугольный треугольник, который образован двумя катетами: высотой h и отрезком r1-r2. Его гипотенуза является генератрисой, она равна:
g = ((r1-r2)^2 + h2)^0,5 = (2,522 + 152 )^0,5 = 15,21 см.
Поскольку известны все необходимые линейные параметры усеченной фигуры, можно воспользоваться известной формулой для площади ее боковой поверхности:
Sb = pi*g*(r1 + r2) = 3,14*15,21*(2,52 + 5,04) = 361,1 см2.
Таким образом, усеченный конус является фигурой вращения, поверхность которой состоит из оснований и боковой части. Чтобы воспользоваться формулами для определения его площади и объема, необходимо знать любые три его линейных параметра.
На этом уроке мы познакомимся с понятием
усеченного конуса. Дадим определение усеченного конуса. Назовем и рассмотрим
его основные элементы. А затем выведем формулы для вычисления площади боковой поверхности
и площади полной поверхности усеченного конуса.
Итак, рассмотрим понятие усечённого конуса.
Вообще вокруг
нас существует множество предметов, имеющих форму усечённого конуса. Вафельные
стаканчики для мороженного имеют форму усечённого конуса, некоторые стаканы, светильники,
ведра обладают формой очень близкой к форме усечённого конуса.
Некоторые
архитектурные сооружения также имеют форму усечённого конуса. И многое другое.
Возьмём произвольный конус и проведём секущую
плоскость, параллельную его основанию. Эта плоскость пересекается с конусом по кругу
и разбивает конус на две части. Одна из частей (верхняя) представляет собой
конус, а вторая (нижняя) называется усечённым конусом.
Определение:
Усечённым конусом называется
часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной
оси конуса.
Назовём элементы усечённого конуса.
Основание исходного конуса и круг, полученный
в сечении этого конуса плоскостью, называются основаниями усечённого
конуса.
Высотой усечённого конуса
называется отрезок (или его длина), соединяющий центры его оснований.
Прямая называется его осью.
Часть конической поверхности, ограничивающая
усеченный конус, называется его боковой поверхностью, а отрезки
образующих конической поверхности, расположенные между основаниями, называются образующими
усечённого конуса.
Все образующие усечённого конуса равны друг
другу.
Усечённый конус может быть получен вращением на
прямоугольной трапеции
вокруг её боковой стороны, перпендикулярной к основаниям.
На экране вы видите усечённый конус,
полученный вращением прямоугольной трапеции вокруг стороны
, перпендикулярной к
основаниям и
. При этом основания усечённого
конуса образуются вращением оснований и
трапеции, а боковая
поверхность – вращением боковой стороны .
Выведем формулу для вычисления площади
боковой поверхности усечённого конуса.
Для этого нам нужно доказать, что площадь
боковой поверхности усечённого конуса равна , где
и
– радиусы оснований,
– образующая усечённого
конуса.
Доказательство. Пусть – вершина конуса, из
которого получен усечённый конус, – одна из образующих
усечённого конуса, а точки и
– центры его оснований.
Причём, . Тогда площадь боковой
поверхности усечённого конуса равна разности боковых поверхностей двух конусов,
т.е. . Преобразуем это
выражение.
Заметим, что длина образующей исходного конуса состоит
из суммы отрезков . Используя формулу для
вычисления площади боковой поверхности конуса, получаем: .
Отсюда, учитывая, что , получим следующее
выражение .
Теперь выразим через
,
и
. Прямоугольные
треугольники подобны
по двум углам. Отсюда следует, что , или
.
Значит, получаем, что .
Подставим это выражение в формулу.
Упростим.
В итоге приходим к следующей формуле: .
Этим мы с вами вывели формулу для
вычисления площади боковой поверхности усеченного конуса.
Таким образом, мы доказали, что площадь
боковой поверхности усечённого конуса равна произведению полусуммы длин
окружностей оснований на длину образующей, где и
– радиусы оснований,
– образующая усечённого
конуса.
Площадью полной поверхности усечённого
конуса называется сумма площадей его боковой поверхности и площади двух
его оснований. Формулу для вычисления площади боковой поверхности усечённого
конуса мы
с вами вывели выше. Площадь нижнего основания усеченного конуса равна , а площадь меньшего
основания – . Подставим все данные в
формулу.
Отсюда, получаем, что площадь полной
поверхности усеченного конуса можно вычислить по следующей формуле: .
Теперь давайте решим несколько задач.
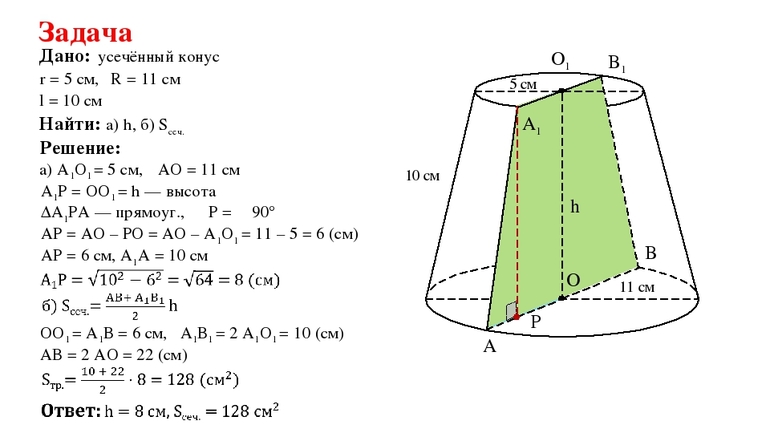
Задача: длины радиусов оснований
и образующей усечённого конуса равны соответственно см,
см и
см. Вычислите его высоту.
Решение: рассмотрим
четырехугольник .
Это есть прямоугольная трапеция с основаниями и
. Высота этой трапеции и
будет высотой нашего усечённого конуса . Для того чтобы её
найти, проведём из точки меньшего основания
перпендикуляр на большее основание трапеции . Фигура
является
прямоугольником, значит противоположные стороны равны, т.е. (см),
.
Рассмотрим . Он прямоугольный (по
построению). Катет (см). Применим теорему
Пифагора и найдём длину катета . Получаем, что
(см). Запишем ответ.
Задача: длины радиусов оснований
усечённого конуса равны см и
см. Вычислите площадь
боковой поверхности этого конуса, если угол между образующей и плоскостью его
основания равен .
Решение: запишем формулу для
вычисления площади боковой поверхности усечённого конуса.
Рассмотрим четырёхугольник .
Это есть прямоугольная трапеция с основаниями и
. Высота этой трапеции и
будет высотой нашего усечённого конуса .
Проведём из точки меньшего основания
перпендикуляр на большее основание трапеции . Фигура
является
прямоугольником, значит, противоположные стороны равны, т.е. (см),
.
Рассмотрим . Он прямоугольный (по
построению). По условию задачи образующая усечённого конуса наклонена к его
основанию под углом . Следовательно, катет
. В свою очередь,
. Применим теорему Пифагора
и найдём длину гипотенузы треугольника
. Получаем, что
(см). Значит, образующая
нашего усечённого конуса равна (см).
Подставим длины радиусов и образующей усечённого
конуса в формулу для вычисления площади боковой поверхности. Посчитаем.
Получим, что площадь боковой поверхности усеченного конуса равна (см2).
Не забудем записать ответ.
Итоги:
На этом уроке мы познакомились с понятием усечённого
конуса. Узнали, что усечённым конусом называется часть конуса, расположенная
между его основанием и секущей плоскостью, перпендикулярной оси конуса. Назвали
основные элементы усечённого конуса. А также вывели формулы для вычисления
площади боковой поверхности и площади полной поверхности усечённого конуса.
План изучения темы
- Понятие конуса.
- Площадь поверхности конуса.
- Объём конуса.
- Усечённый конус.
- Площадь поверхности усечённого конуса.
- Объём усечённого конуса.
- Решение задач на тему «Конус».
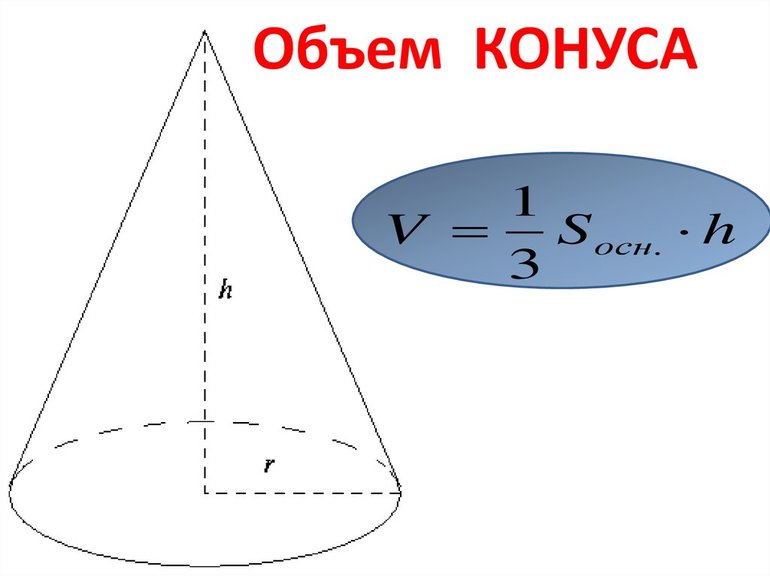
Понятие конуса
Конус — геометрическое тело, образованное конической поверхностью и пересекающей её плоскости, не проходящей через точку Р (рисунок выше). Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета. На рисунке ниже треугольник РОА вращают вокруг катета РО.

Площадь поверхности конуса
Как и цилиндр, конус имеет два вида площадей — площадь боковой поверхности и площадь полной поверхности.
Развёртка конуса представляет собой сектор. Отсюда есть разные формулы нахождения площади боковой поверхности.
Это формула при использовании развёртки, как сектора. Если же учесть, что длина дуги сектора равна длине окружности основания конуса, то получаем равенство:
где r — радиус основания конуса. Тогда имеем вторую, более простую формулу нахождения площади боковой поверхности конуса:
Площадь полной поверхности состоит из боковой и основания конуса. Значит, формула нахождения этой площади:
 Объём конуса
Объём конуса
где r — радиус основания конуса, h — высота конуса.
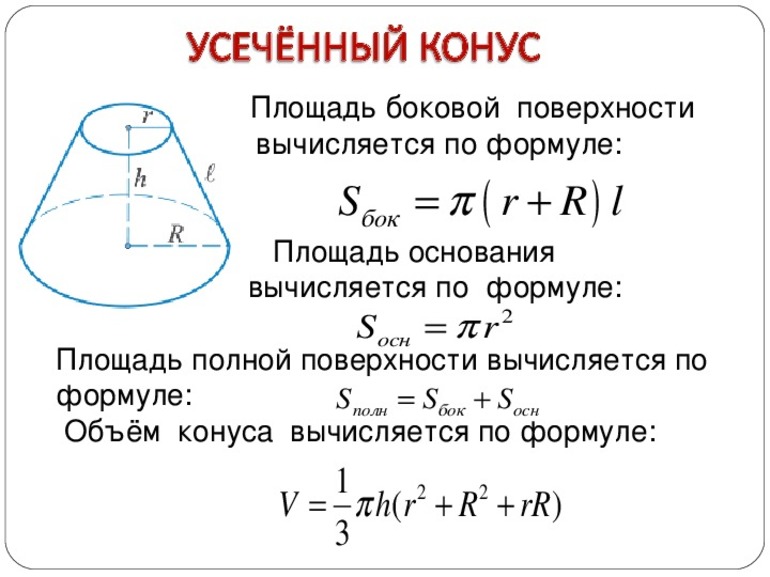
Усечённый конус

Площадь поверхности усечённого конуса
Из-за того, что теперь у нас два основания, формула площади боковой поверхности усеченного конуса будет выглядеть иначе:
Само собой, меняется и формула площади полной поверхности:
 Объём усечённого конуса
Объём усечённого конуса
 Решение задач на тему «Конус»
Решение задач на тему «Конус»
Пример 1 (Ященко 36 вариантов, 2021 год, вариант 7)
В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости составляет 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд.

Высота налитой жидкости 0,25 от всей высоты конуса. Значит, высота в 4 раза больше. Но при этом, не забывайте, что радиус всего конуса тоже увеличится в 4 раза. Так как мы на осевом сечении получаем случай подобных треугольников:

Видим, что объём всего конуса в 64 раза больше налитой жидкости. Значит, в миллилитрах это будет:
Получается, что долить нужно 315 миллилитров.
Ответ: 315
Пример 2 (Ященко 36 вариантов, 2021 год, вариант 11)
Цилиндр и конус имеют общее основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.


Ответ: 54
Пример 3 (Ященко 36 вариантов, 2021 год, вариант 25)
Площадь боковой поверхности конуса равна 30. Параллельно основанию конуса проведено сечение, делящее его высоту в отношении 2:3, считая от вершины конуса. Найдите площадь боковой поверхности отсечённого конуса.


Отсечённый конус — это тот, что сверху, маленький. Значит, с учётом коэффициента подобия:

Объем и площадь усеченного конуса
Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Радиус основания 1
см
Радиус основания 2
см
Высота
см
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что считает калькулятор?
Калькулятор объема и площади усеченного конуса — это онлайн инструмент, который используется для быстрого расчета объема и площади усеченного конуса по его радиусам большего и меньшего оснований и высоте. Объем такого конуса представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.
Калькулятор объема и площади усеченного конуса может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов и площадей таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов и площадей, например, в архитектуре, инженерии, физике и т.д.
Где можно применить калькулятор объема и площади усеченного конуса?
Калькулятор объема и площади усеченного конуса может применяться в различных сферах, включая:
- Инженерия и строительство: усеченный конус может использоваться в качестве формы для создания конструкций и деталей, таких как колонны, башни, фонари, вазы и т.д. такие расчеты помогают определить необходимое количество материала для изготовления детали.
- Производство: усеченный конус может использоваться в качестве формы для изготовления различных изделий из металла, стекла, керамики, пластика и т.д. Расчёт его параметров помогает определить необходимое количество сырья для производства изделия.
- Математика: усеченный конус может быть использован для примеров и задач в математическом образовании. Расчёт объёма и площади позволяет ученикам узнать, как применять формулы для нахождения объёма и площади фигур.
- Машиностроение: усеченный конус может использоваться в качестве детали для различных механизмов и машин. Расчёт объёма и площади помогает определить размеры и форму детали.
- Архитектура и дизайн: усеченный конус может использоваться в качестве элемента декора и оформления интерьера и экстерьера зданий. Расчёт объёма и площади помогает определить оптимальный размер и форму элемента декора.
В чем преимущество усеченного конуса как геометрической фигуры?
Усеченный конус — это геометрическая фигура, у которой основаниями являются две круглые плоскости, соединенные боковой поверхностью, которая имеет форму конуса, но сечение вдоль его высоты меньше его оснований.
Преимущества этой геометрической фигуры могут включать:
- Усеченный конус имеет большую устойчивость, чем обычный конус, так как он имеет большую поверхность опоры на основаниях, что делает его лучшим выбором для некоторых приложений, например, при проектировании оболочек реакторов.
- Усеченный конус может быть более экономичным в использовании материала, чем обычный конус, так как он имеет меньшую высоту, но сохраняет ту же площадь оснований. Это может быть полезно в проектировании строительных элементов, таких как колонны или башни.
- Усеченный конус может иметь большую универсальность в применении, так как его форма может быть изменена путем изменения размеров его оснований и высоты. Это позволяет использовать усеченные конусы в различных областях, например, в качестве башенной опоры или формы для литья металла.
- Усеченный конус может иметь более эргономичную форму, что делает его удобным в использовании в некоторых приложениях, например, при проектировании мебели или автомобильных деталей.
- Усеченный конус может иметь более интересный внешний вид, что делает его привлекательным для использования в художественном дизайне или архитектуре.
В целом, усеченный конус является полезной геометрической фигурой, которая имеет множество преимуществ в различных областях применения.
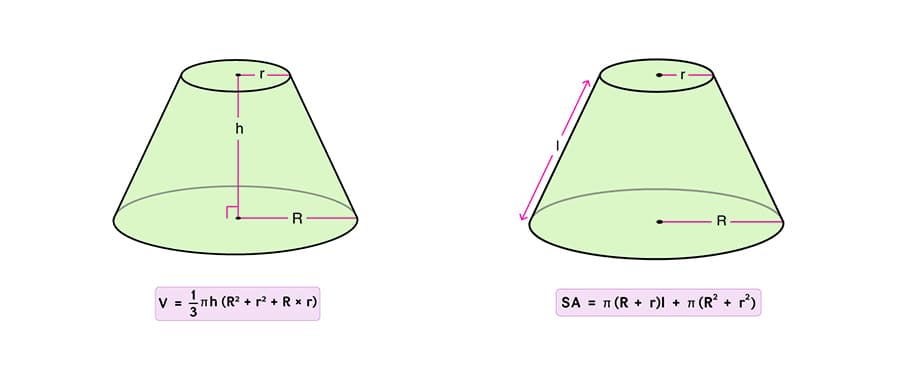
Как вычислить объем усеченного конуса через радиусы его оснований и высоту?
Для расчета объема усеченного конуса необходимо знать радиусы большего и меньшего оснований, а также высоту усеченного конуса.
Формула для расчета объема усеченного конуса:
V = (1/3) * π * h * (R2 + Rr + r2)
где:
- π — число Пи (3.14)
- V — объем усеченного конуса
- h — высота усеченного конуса
- R — радиус большего основания
- r — радиус меньшего основания
Чтобы использовать эту формулу, нужно знать значения h, R и r. Затем необходимо подставить значения в формулу и выполнить вычисления.
Пример:
Допустим, у нас есть усеченный конус с высотой 10 см, радиусом большего основания 6 см и радиусом меньшего основания 4 см. Чтобы найти объем усеченного конуса, мы можем использовать формулу:
- V = (1/3) * π * h * (R2 + Rr + r2)
- V = (1/3) * 3,14 * 10 * (6^2 + 6*4 + 4^2)
- V = 795,5 см3
Ответ: объем усеченного конуса равен 795,5 кубическим сантиметрам.
Как вычислить площадь усеченного конуса через радиусы его оснований и образующую?
Площадь усеченного конуса можно рассчитать с использованием следующей формулы:
S = π(r + R)ℓ + π(R2 + r2)
- где S — площадь усеченного конуса,
- π — математическая константа, примерно равная 3.14,
- r1 и r2 — радиусы оснований большего и меньшего конусов соответственно,
- и ℓ — образующая, т.е. расстояние между вершиной и основанием, вычисленная по теореме Пифагора.
Для решения задачи необходимо знать значения радиусов оснований и образующей. Если известны только высоты обоих конусов, то необходимо использовать теорему Пифагора для вычисления образующей.
После подстановки всех известных значений в формулу можно вычислить площадь усеченного конуса.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.
Как пользоваться онлайн калькулятором объема и площади усеченного конуса?
Для того, чтобы использовать калькулятор объема усеченного конуса, нужно ввести значения радиусов его оснований и высоту в соответствующие поля калькулятора, затем калькулятор автоматически рассчитает объем шара. Для расчёта площади нужно проделать соответствующие действия со значениями радиусов оснований и образующей, которая вычисляется по теореме Пифагора.
Что такое усеченный конус?
Усеченный конус — это геометрическое тело, полученное из обычного конуса путем удаления верхней части тела параллельным срезом, расположенным на определенном расстоянии от вершины конуса.
Для чего нужен расчет объема усеченного конуса?
Расчет объема и площади усеченного конуса может быть полезен во многих областях, включая инженерию, архитектуру, производство и технику. Например, в производственной отрасли расчет объема и площади усеченного конуса может помочь определить количество материалов, необходимых для создания детали.
Какой материал лучше всего подходит для изготовления усеченных конусов?
Для изготовления усеченного конуса можно использовать различные материалы в зависимости от требований к конструкции. Однако, наиболее распространенными материалами для изготовления усеченных конусов являются металлы. Это может быть сталь, алюминий, медь, латунь и другие металлы. Металлические конусы обычно используются в технических приложениях, где требуется высокая прочность и устойчивость к износу.
Как вычислить образующую усеченного конуса?
Образующая конуса (l) может быть найдена с помощью теоремы Пифагора, для этого можно воспользоваться формулой: l = √((R — r)² + h²). Таким образом, чтобы вычислить образующую усеченного конуса, необходимо знать значения радиуса большего основания, радиуса меньшего основания и высоты конуса, после чего следует применить формулу, описанную выше.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
- Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
- Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
- Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии