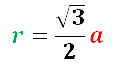Как найти длину окружности вписанной в шестиугольник - Исправление недочетов и поиск решений вместе с Examum.ru

Окружность, вписанная в правильный шестиугольник

Содержание:

Что такое правильный шестиугольник
Основные свойства правильного шестиугольника
Нахождение радиуса вписанной окружности
- Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника
Периметр правильного шестиугольника

Что такое правильный шестиугольник

Правильный шестиугольник или гексагон — выпуклый шестиугольник, у которого все стороны и углы равны.

шестиугольник

Сумма всех углов n–угольника равна 180°(n−2). Каждый угол правильного n–угольника равен (α_n=frac{left(n-2right)}n180°). Следовательно углы правильного шестиугольника равны (frac{left(6-2right)}6180°=120°).

Основные свойства правильного шестиугольника

У гексагона все внутренние углы равны между собой.
Каждый внутренний угол правильного шестиугольника равен 120°.
Все стороны гексагона равны между собой.
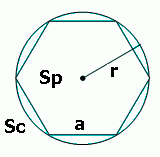
Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
Большая диагональ правильного шестиугольника равна диаметру описанной около него окружности или сумме двух его сторон.
Меньшая диагональ правильного шестиугольника в (sqrt3) раз больше его стороны.
Меньшая диагональ правильного шестиугольника и две его противолежащие стороны перпендикулярны друг другу.
Меньшая диагональ правильного шестиугольника равна удвоенному радиусу вписанной в него окружности.
Правильный шестиугольник замещает плоскость, это значит заполняет ее без пробелов и наложений.
Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равных равносторонних треугольников. Высота этих треугольников равна радиусу вписанной в правильный шестиугольник окружности.
При поворотах относительно центра на угол, кратный 60°, правильный шестиугольник переходит в себя.
Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями — прямоугольный. Гипотенузой такого треугольника является большая диагональ. Его острые углы равны 30° и 60°.

шесть равных треугольников.jpg

свойства правильного шестиугольника.jpg

У изображенного правильного шестиугольника ∠А=∠В=∠С=∠D=∠Е=∠F=120°. Стороны равны между собой АВ=ВС=СD=DE=EF=FA. Точка О — центр пересечения диагоналей. Большая диагональ AD=2АВ. Меньшая диагональ (СА=sqrt3·АВ).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема 1

В любой правильный шестиугольник можно вписать окружность, и притом только одну.

Следствие из теоремы:

Центры вписанной и описанной окружности у правильного шестиугольника (как и у любого правильного многоугольника) совпадают.
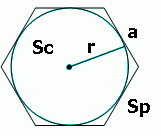
Радиус вписанной окружности равен перпендикуляру, проведенному из центра к любой стороне правильного шестиугольника.

Нахождение радиуса вписанной окружности

шестиугольник правильный вписанная окружность.jpg

В шестиугольник АВСDEF вписана окружность. Ее центр находится на пересечении диагоналей в точке О. Если известна сторона данного шестиугольника, то можно найти радиус вписанной окружности, рассмотрев прямоугольный треугольник (А_1ОВ). Гипотенуза (ΔА_1ОВ) равна стороне шестиугольника, ОВ=АВ. Перпендикуляр (ОА_1) делит сторону АВ пополам, то есть (А_1В=frac12·АВ=frac12·ОВ). Так как (ОВ^2=ОА_1^2+А_1В^2), то (ОА_1=sqrt{ОB^2-A_1В^2}=sqrt{ОB^2-A_1В^2}=sqrt{0B^2-left(frac12cdot0Bright)^2}=frac{sqrt3}2OB). Получаем следующую формулу:

Формула 1

(r=frac{sqrt3}2·a)

где r — радиус окружности, вписанной в правильный шестиугольник,

а — сторона правильного шестиугольника.

Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника

Существует классическая формула, с помощью которой можно вычислить радиус окружности, вписанной в любой правильный многоугольник.

Формула 2

(r=frac a{2tgfrac{180^0}n})

где r — радиус окружности, вписанной в правильный многоугольник,

а — сторона правильного многоугольника,

n — количество вершин многоугольника.

Для правильного шестиугольника n=6.

(r=frac a{2tgfrac{180^0}6}=frac a{2tg30^0}.)

Так как (tg30^0=frac1{sqrt3}), то (r=frac{sqrt3}2·a). То есть, получаем формулу, найденную выше.

Периметр правильного шестиугольника

Если известен радиус вписанной окружности, то периметр правильного шестиугольника можно найти по формуле:

Формула 3

(Р=4sqrt3r)

где Р — периметр правильного шестиугольника,

r — радиус вписанной в него окружности.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Шестиугольник является правильным многоугольником, так как у него все стороны и углы равны. А значит, в любой шестиугольник можно вписать окружность.

Точка O –центр правильного многоугольника, также является центром вписанной в него окружности.
Центр правильного многоугольника равноудален от его сторон. Отрезок, соединяющий центр с точкой касания вписанной окружности называется апофемом и является радиусом вписанной окружности.

Существует классическая формула для нахождения радиуса вписанной окружности в правильный многоугольник

$r={ a / { 2tg{{180^0}/n}} }$

Для правильного шестиугольника n=6, тогда угол будет равен ${{180^0}/6}=30^0$
По тригонометрической таблице tg(30°)=
Тогда формула радиуса вписанной окружности в шестиугольник имеет следующий вид
Радиус вписанной окружности в шестиугольник равен половине произведения стороны и корня квадратного из 3

Пример расчета радиуса окружности вписанной в шестиугольник
Найдите радиус окружности вписанной в правильный шестиугольник со стороной 6
Применив формулу радиуса вписанной окружности в шестиугольник, имеем

Источник

Радиус вписанной окружности в шестиугольник

Радиус вписанной окружности

По определению, правильным шестиугольником является выпуклый многоугольник с шестью вершинами и шестью равными сторонами и внутренними углами. Сумма его углов определяется, как произведение 180° на (n-2), при этом n — количество сторон, равное в данном случае 6. Соответственно, сумма углов составит 720° (180° х (6 — 2)), а величина внутреннего угла — 120°. В правильный шестиугольник можно легко вписать окружность. Стороны шестиугольника будут касательны к вписанной окружности. Центры правильного шестиугольника и вписанной окружности совпадают.
Радиус вписанной окружности рассчитывается по формуле:

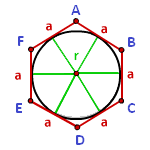
а — сторона шестиугольника.

Т.е. радиус равняется половине корня из трех, умноженному на величину его стороны. В правильном 6-угольнике радиус R описанной окружности равняется его стороне. Следовательно, r вписанной окружности можно рассчитать, как половину корня из трех, умноженному на R описанной окружности.

Быстро и правильно рассчитать радиус вписанной в заданный 6-угольник окружности можно с помощью онлайн калькулятора.

Источник

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические
43,666
гуманитарные
33,654
юридические
17,917
школьный раздел
611,992
разное
16,906

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Источник

На самом деле у меня уже были сделаны калькуляторы для правильных многоугольников — Длина стороны правильного многоугольника. Один из первых запросов пользователей, между прочим. Эти калькуляторы находили параметры правильного многоугольника, исходя из величины радиуса описанной или вписанной в него окружности.

Калькуляторы ниже решают обратную задачу — исходя из параметров многоугольника, находят параметры вписанной и описанной окружностей.
Радиус вписанной окружности (incircle):
$r_i=frac{a}{2tan(pi/n)}$