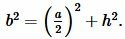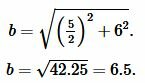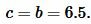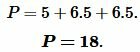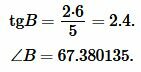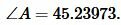Как найти длину основания прямоугольного равнобедренного треугольника

Калькулятор основания прямого равнобедренного треугольника через длину ребер

При помощи данного калькулятора можно вычислить длину основания у равнобедренного прямого треугольника.

Ребро треугольника A

У равнобедренного прямого треугольника один из трех углов равен 90°, а два ребра (стороны), которые начинаются с этого угла равны между собой, два оставшихся угла равны 45°.

Для вычисления основания у прямого равнобедренного треугольника зная длину его ребер необходимо воспользоваться следующей формулой:
y = A√2
где:
y — основание треугольника
A — длина стороны равнобедренного прямого треугольника.

Как посчитать стороны равнобедренного треугольника

Онлайн калькулятор

Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

• длину основания (b) и угол α
• длину основания (b) и угол β
• длину основания (b) и высоту (h)

• длину двух равных сторон (a) и угол α
• длину двух равных сторон (a) и угол β
• длину двух равных сторон (a) и высоту (h)

Введите их в соответствующие поля и получите результат.

Как посчитать сторону a равнобедренного треугольника

Если известна сторона b и угол α

Чему равна сторона a равнобедренного треугольника если длина основания , а угол

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?

Формула

Пример

Если сторона b = 10 см, а ∠α = 30°, то:

Если известна сторона b и угол β

Чему равна сторона a равнобедренного треугольника если длина основания , а угол

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?

Формула

Пример

Если сторона b = 10 см, а ∠β = 30°, то:

a = 10 /_{2⋅sin 15} = 10/(2⋅0.2588) = 19.31см

Если известна сторона b и высота h

Чему равна сторона a равнобедренного треугольника если длина основания , а высота

Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?

Формула

Пример

Если сторона b = 10 см, а высота h = 20 см, то:

a = √ 1 /_{10 2} + 20 2 = √ 0.01+400 = 20.61см

Как посчитать сторону b (основание) равнобедренного треугольника

Если известна сторона a и угол α

Чему равна сторона b равнобедренного треугольника если длина стороны , а угол

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

Пример

Если сторона a = 10 см, а ∠α = 30°, то:

b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см

Если известна сторона a и угол β

Чему равна сторона b равнобедренного треугольника если длина стороны , а угол

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

Пример

Если сторона a = 10 см, а ∠β = 40°, то:

Если известна сторона a и высота h

Чему равна сторона b равнобедренного треугольника если длина стороны , а высота

Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?

Формула

b = 2⋅ √ a 2 — h 2 , h

Пример

Если сторона a = 10 см, а высота h = 5 см, то:

Равнобедренный прямоугольный треугольник

Средняя оценка: 4.1

Всего получено оценок: 277.

Средняя оценка: 4.1

Всего получено оценок: 277.

И равнобедренный, и прямоугольный треугольник достаточно привычны любому, кто знаком с геометрией. Сочетание этих признаков встречается довольно редко и плохо поддается визуальному восприятию. Не всегда можно представить полный набор свойств такого треугольника, поэтому поговорим о нем более подробно.

Определение

Равнобедренный треугольник – это треугольник, боковые стороны которого равны. Прямоугольный треугольник содержит в себе прямой угол. Значит равнобедренный прямоугольный треугольник – это прямоугольный треугольник, катеты которого равны.

Гипотенуза прямоугольного треугольника всегда больше катета. Это следует из теоремы о соотношениях сторон и углов треугольника. Значит, в прямоугольном треугольнике только гипотенуза может быть основанием, а величина гипотенузы будет соответствовать длине основания.

Свойства

Поговорим подробнее о свойствах и формулах. Не совсем ясно, как будут проходить высоты в таком треугольнике, все привыкли пользоваться свойством, которое говорит о том, что в равнобедренном треугольнике высота, проведенная к основанию, совпадает с медианой и биссектрисой.

В равнобедренном прямоугольном треугольнике такая высота всегда будет направлена из прямого угла к гипотенузе. А две другие высоты будут совпадать с катетами.

Рис. 2. Высота прямоугольного равнобедренного треугольника

Если к гипотенузе прямоугольного равнобедренного треугольника провести высоту, то она разделит треугольник на два, равных между собой, равнобедренных прямоугольных треугольника.

Теорема Пифагора для равнобедренного треугольника выглядит немного упрощенной:

Квадрат гипотенузы равен удвоенному квадрату катета. Это значительно упрощает решение.

Вообще, любые задачи, связанные с прямоугольными равнобедренными треугольниками, решаются очень просто. Любого значения достаточно, чтобы определить все остальное. Значения любого из катетов достаточно, чтобы определить гипотенузу через упрощенную теорему Пифагора, а затем найти периметр и площадь прямоугольного равнобедренного треугольника.

Через гипотенузу можно найти катет и через тригонометрическую функцию, так как все углы прямоугольного равнобедренного треугольника заранее известны: один угол 90 градусов и два по 45.

Рис. 3. Углы прямоугольного равнобедренного треугольника

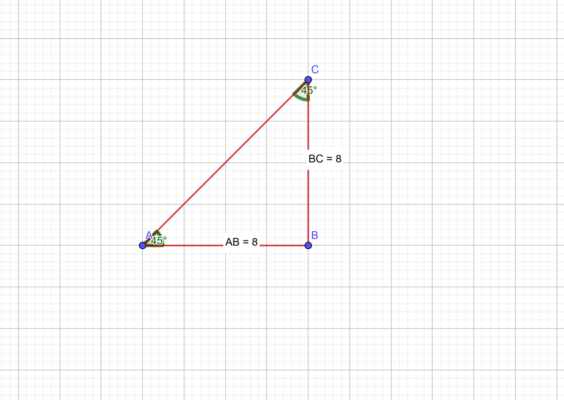
Разберем подробно, почему известны все углы. В любом прямоугольном треугольнике сумма острых углов равна 90 градусам. Это следует из общей суммы углов в треугольнике, которая всегда равна 180 градусам.

При этом углы при основании равнобедренного треугольника, а в нашем случае это всегда гипотенуза, всегда равны. Значит, чтобы найти каждый из острых углов при гипотенузе, нужно их сумму, т.е. 90 градусов, разделить пополам. Получается, что каждый из углов при гипотенузе прямоугольного равнобедренного треугольника будет равен 45 градусам.

Можно рассмотреть это свойство и с другой стороны: если сумма двух углов треугольника равняется 90 градусам и эти углы равны между собой, то этот треугольник является равнобедренным и прямоугольным.

Из этого же свойства вытекает равенство синусов и косинусов острых углов прямоугольного равнобедренного треугольника между собой, а также равенство их тангенсов и котангенсов.

То есть, синус любого острого угла прямоугольного равнобедренного треугольника равен косинусу любого острого угла данного треугольника и равен $$<sqrt<2>over2>$$. Тангенс любого острого угла прямоугольного равнобедренного треугольника равен котангенсу любого острого угла данного треугольника и равен 1.

Что мы узнали?

Мы подробно поговорили о всех взаимосвязях свойств прямоугольного и равнобедренного треугольника. А также о том, как эти связи проявляются в равнобедренном прямоугольном треугольнике. Разобрали в подробностях, почему любые задачи на нахождение параметров прямоугольного равнобедренного треугольника легко решаются и выделили основную и единственную проблему в решениях таких задач: трудность визуального восприятия.

Равнобедренный треугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

Определение равнобедренного треугольника

Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.

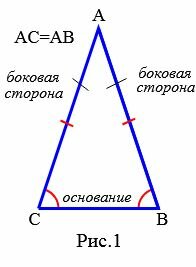
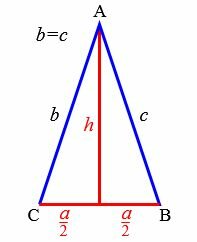
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).

Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.

Существует более общее определение равнобедненого треугольника:

Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.

Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.

Теорема о равнобедренном треугольнике

Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.

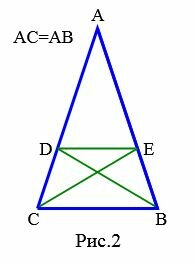
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:

( small angle ACE=angle ABD.)

(2)

Из ( small AB=AC) и ( small AD=AE ) следует:

Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что

( small angle ECB= angle DBC. )

(4)

Из (2) и (4) следует, что ( small angle B= angle C. )

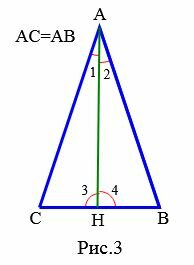
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )

Свойства равнобедренного треугольника

Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.

Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.

Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.

Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:

Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.

Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.

Признаки равнобедренного треугольника

Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.

Признак 1 следует из определения 1.

Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.

Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).

Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда

( small angle 1=angle2, ) ( small CH=HB. )

(5)

Применим теорему синусов для треугольника ( small AHC ):

( small frac <large CH><large sin angle 1>= frac <large AH><large sin angle C>. )

(6)

Применим теорему синусов для треугольника ( small AHB ):

( small frac <large HB><large sin angle 2>= frac <large AH><large sin angle B>. )

(7)

тогда, из (5), (6), (7) получим:

( small frac <large AH><large sin angle C>= frac <large AH><large sin angle B>. )

(8)

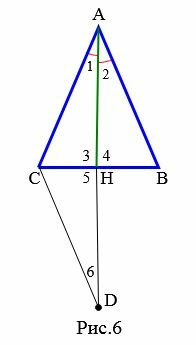
Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° — angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )

Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне

Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.

Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине

Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.

Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.

3. Признак равенства равнобедренных треугольников по основанию и углу при основании

Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.

Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.

Задачи и решения

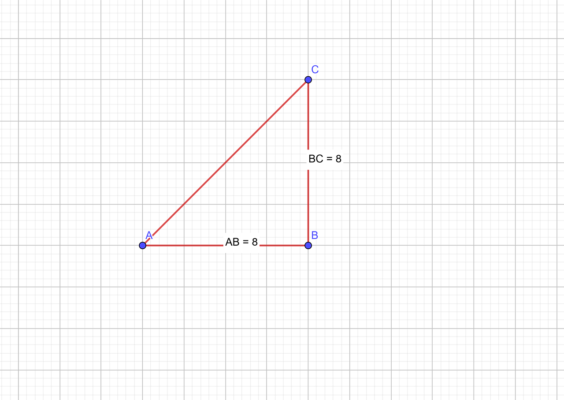
Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.

Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:

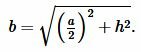(9)

Подставляя значения ( small a ) и ( small h ) в (9), получим:

Боковая сторона ( small c ) равнобедренного треугольника равна:

Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:

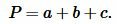(10)

Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:

Найдем угол ( small B ) равнобедренного треугольника:

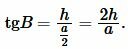(11)

Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:

Тогда угол ( small C ) равнобедренного треугольника равен:

Поскольку сумма всех углов треугольника равна 180°, то имеем:

Площадь треугольника можно вычислить из формулы:

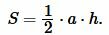(12)

Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:

Как найти длину основания равнобедренного треугольника

Треугольник – это часть плоскости, ограниченная тремя отрезками прямых, имеющими попарно по одному общему концу. Отрезки прямых в данном определении называются сторонами треугольника, а их общие концы – вершинами треугольника. Если две стороны треугольника равны, то его называют равнобедренным.

Инструкция

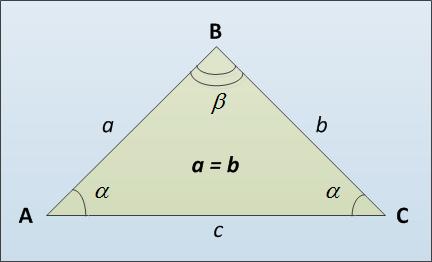
Основанием треугольника называется третья его сторона AC (см. рисунок), возможно отличная от боковых равных сторон AB и BC. Приведем несколько способов вычисления длины основания равнобедренного треугольника. Во-первых, можно воспользоваться теоремой синусов. Она гласит, что стороны треугольника прямо пропорциональны значению синусов противолежащих углов: a / sin α = c / sin β. Откуда получаем, что c = a * sin β / sin α.

Приведем пример вычисления основания треугольника по теореме синусов. Пусть a = b = 5, α = 30°. Тогда по теореме о сумме углов треугольника β = 180° — 2 * 30° = 120°. с = 5 * sin 120° / sin 30° = 5 * sin 60° / sin 30° = 5 * √3 * 2 / 2 = 5 * √3. Здесь для вычисления значения синуса угла β = 120° мы воспользовались формулой приведения, согласно которой sin (180° — α) = sin α.

Второй способ найти основание треугольника – при помощи теоремы косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла, заключенного между ними. Получаем, что квадрат основания c^2 = a^2 + b^2 – 2 * a * b * cos β. Далее находим длину основании c, извлекая квадратный корень из данного выражения.

Рассмотрим пример. Пусть нам заданы такие же параметры, как в предыдущей задаче (см. пункт 2). a = b = 5, α = 30°. β = 120°. с^2 = 25 + 25 — 2 * 25 * cos 120° = 50 — 50 * (- cos 60°) = 50 + 50 * ½ = 75. В данном вычислении мы также применили формулу приведения для нахождения cos 120°: cos (180° — α) = — cos α. Извлекаем квадратный корень и получаем значение c = 5 * √3.

Рассмотрим частный случай равнобедренного треугольника – прямоугольный равнобедренный треугольник. Тогда по теореме Пифагора мы сразу же находим основание c = √(a^2 + b^2).

Видео по теме

Обратите внимание

При вычислении легко ошибиться в значениях синуса или косинуса угла, или просто в арифметических действиях. Для проверки разультата полезно вычислить длину основания двумя способами.

Полезный совет

При вычислении угла, противолежащего к основанию, будет удобно использовать следующие формулы приведения: sin (180° — α) = sin α; cos (180° — α) = — cos α.

Источники:

• как найти длину стороны в равнобедренном треугольнике
• Медианы, биссектрисы и высоты треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Равнобедренный треугольник — это треугольник, у которого 2 стороны равны. Равные стороны — это рёбра, а 3 сторона — основание. Вариант 1 Если известно, чему равна боковая сторона, а также высота, опущенная на основание. Как известно, высота перпендикулярна основанию, а в случае с равнобедренным треугольником она разбивает его на 2 равных прямоугольных треугольника. Можно по теореме Пифагора найти половину основания, а затем это значение умножить на 2. Вот формула: b = 2√(a² — h²) Вариант 2 Если известно, чему равна боковая сторона и один из углов. Нужно воспользоваться теоремой синусов: a/sinα = b/sinβ = c/sinγ. c = (a*sinγ)/sinα. Так как в равнобедренном треугольнике углы при основании равны, то легко можно найти 2 оставшихся угла, исходя из того, что сумма 3 углов равна 180 градусов. система выбрала этот ответ лучшим Алиса в Стран­е [364K] 5 лет назад  К сожалению у нас нет условия задачи, из которой было бы ясно — на основании каких данных мы должны искать основание нашего равнобедренного треугольника (две стороны боковые которого равны между собой, а основание — это нижняя сторона, которая как раз двум другим не равна). Поэтому рассмотрим несколько вариантов. 1.) Допустим, мы знаем, чему равна боковая сторона и угол треугольника (любой из трех). Тогда мы сначала легко вычисляем два других угла треугольника, помня, что их сумма всегда равна 180 градусам, а затем применяем теорему синусов: следовательно с (основание) будет равно: 2.) Допустим, мы знаем чему равна боковая сторона и высота нашего треугольника. Тогда мы сначала находим половину его основания (она является катетом треугольника, полученного делением исходного равнобедренного треугольника его высотой на два прямоугольных треугольника), применив теорему Пифагора. где с — основание треугольника, которое мы ищем, h — его высота. Марин­а Волог­да [295K] 5 лет назад  Чтобы найти основание равнобедренного треугольника, необходимо вспомнить геометрию. Что такое равнобедренный треугольник — это треугольник, в котором две из трех сторон равны. Теперь вспомним что такое основание треугольника — это как раз третья сторона, которая не равна остальным двум. Так как у нас нет никаких данных задачи, значит следует указать только формулы, по которым можно найти основание. Основание можно найти применив теорему Пифагора по формуле: b = 2√(a² — h²) где h — это высота опущенная на основание; а -сторона треугольника. Чтобы понять, как правильно решать, вот примерная задача: А вот решение для задачи: JuliG­or [3.2K] 9 лет назад  Для того, чтобы найти основание равнобедренного треугольника? нам необходимо знать или один из углов, или же высоту треугольника, которая проводится к его основанию. Основание можно вычислить по следующей, вполне легкой формуле: где b — длина основания треугольника; a — длина стороны треугольника; B — это угол, который противоположен основанию. Alen4­uk [161K] 5 лет назад  Для начала вспомним, какой треугольник называется равнобедренным и из этих его свойств будем уже находить величину основания. Как видим из рисунка, равнобедренный треугольник- это треугольник, у которого две стороны равны и они называются боковыми. Третья же сторона является основанием этого треугольника. Равные стороны называются боковыми. Какие же свойства имеет равнобедренный треугольник, которые помогут нам найти его основание? Углы при основании у равнобедренного треугольника равны между собой. Высота, которую мы опускаем с верхнего угла на основание одновременно является и биссектрисой и медианой. Чтобы найти площадь равнобедренного треугольника нужно разделить на 2 произведение основания на высоту, проведенную к этому основанию. К сожалению, нам не даны условия задачи, поэтому можно использовать несколько формул. Все будет зависеть от данных задачи. Используя эти свойства, мы для нахождения основания можем использовать следующие формулы: Так же нам может помочь в решении теорема синусов. Бекки Шарп [71.2K] 5 лет назад  При решении задач с равнобедренным треугольником нужно использовать свойства как равнобедренного треугольника, так и прямоугольного, поскольку высота равнобедренного треугольника делит его на 2 одинаковых прямоугольных. Основание равнобедренного треугольника ищется, когда есть какие-то исходные данные. Например известны сторона и угол. Тогда поступаем следующим образом: Находим третий угол ( 180 градусов минус сумму двух углов) и используем теорему косинусов: где АС -основание, АВ и ВС — стороны. Рассмотри задачу, когда известны стороны равнобедренного треугольника. Тогда основание ищется, используя теорему Пифагора. Вот здесь нам и понадобится разделить равнобедренный треугольник на два прямоугольных. В итоге основание АС будет равно — 2 квадратных корня из разности квадратов стороны АВ и высоты ВН. 12777­1 [273K] 5 лет назад  Для начала нужно понять, что такое равнобедренный треугольник, таким треугольником называют треугольник у которого две стороны равны. Ниже рисунок такого треугольника: К сожалению нет данных в вопросе. Например, если задана площадь и высота ВH. Тогда основание (на рисунке выше сторона АС) будет равна площадь разделить на высоту BH и умножить на 0,5. Если же нам известна одна сторона и высота треугольника, можно воспользоваться теоремой Пифагора. Ниже представлена формула, по которой можно вычислить основание: b = 2√(a² — h²). Возможно и другие варианты, например, если известна сторона и угол, тогда можно воспользоваться теоремой косинусов или синусов. Nelli­4ka [114K] 5 лет назад  Можно найти для начала значение половины основания, а затем умножить это значение на два. Смысл в том, что мы опускаем на основание из противоположного угла высоту (она в равнобедренном треугольнике совпадает с биссектрисой и медианой), получается два прямоугольных треугольника. Вспоминаем теорему Пифагора, вычисляем разницу между гипотенузой и высотой, извлекаем корень. Конечно, в этом случае по условиям задачи нам должно быть известно значение высоты. Если же известно значение боковой стороны и противоположного основанию угла, то легче всего пойти через формулу синусов: Также можно воспользоваться формулой косинусов: Барха­тные лапки [382K] 5 лет назад  Равнобедренный треугольник — это треугольник у которого две стороны одинаковые, они боковыми, а третья сторона — это основание. Чему равняется основание возможно узнать, если у нас есть данные чему равна одна боковая сторона (а вторая боковая будет равняться также) и высота. В этом случае воспользуемся такой формулой: b = 2(a — h). Как уже видно, для этого нам нужно знать значение боковой стороны и высоты (которая в равнобедренном треугольнике будет такая же как медиана и биссектриса). Но также можно решить эту задачку и другим способом, для этого должны знать чему равняется боковая сторона и один из углов. kkkar­atist­tt [7.7K] 5 лет назад  В задачах такого типа всегда даётся вариант, где у вас известен один угол, если вы знаете одну сторону угла равнобедренного треугольника. То вы умножаете значения на два угла и высоту равнобедренного треугольника. Таким образом вы получите чему равно основание этого треугольника. Бисектриса тоже может вам помоч. Знаете ответ?

The Pythagorean Theorem, an equation that shows the relationship between a right triangle’s three sides, can help you to find the length of its base. A triangle that contains a 90-degree or right angle in one of its three corners is called a right triangle. A right triangle’s base is one of the sides that adjoins the 90-degree angle.

The Pythagorean Theorem

The Pythagorean Theorem is a formula that gives the relationship between the lengths of a right triangle’s three sides. The triangle’s two legs, the base and height, intersect the triangle’s right angle. The hypotenuse is the side of the triangle opposite the right angle. In the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides:

a^2 + b^2 = c^2

In this formula, ​​a​​ and ​​b​​ are the lengths of the two legs and ​​c​​ is the length of the hypotenuse. The ^​2​ signifies that ​​a​​, ​​b​​, and ​​c​​ are ​squared​. A number squared is equal to that number multiplied by itself – for example, 4² is equal to 4 times 4, or 16.

Finding the Base

Using the Pythagorean theorem, you can find the base, ​a​, of a right triangle if you know the lengths of the height, ​b​, and the hypotenuse, ​c​. Since the hypotenuse squared is equal to the height squared plus the base squared, then:

a^2 = c^2 — b^2

For a triangle with a hypotenuse of 5 inches and a height of 3 inches, find the base squared:

c^2 — b^2 = (5 × 5) — (3 × 3) = 25 — 9 = 16 \ implies a = 4

Since b² equals 9 , then ​a​ equals the number that, when squared, makes 16. When you multiply 4 by 4, you get 16, so the square root of 16 is 4. The triangle has a base that is 4 inches long.

A Man Called Pythagoras

The Greek philosopher and mathematician, Pythagoras, or one of his disciples, is attributed with the discovery of the mathematical theorem still used today to calculate the dimensions of a right triangle. To complete the calculations, you must know the dimensions of the longest side of the geometric shape, the hypotenuse, as well as another one of its sides.

Pythagoras migrated to Italy in about 532 BCE because of the political climate in his own country. Besides being credited with this theorem, Pythagoras – or one of the members of his brotherhood – also determined the significance of numbers in music. None of his writings have survived, which is why scholars don’t know if it was Pythagoras himself who discovered the theorem or one of the many students or disciples who were members of the Pythagorean brotherhood, a religious or mystical group whose principles influenced the work of Plato and Aristotle.