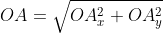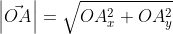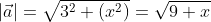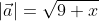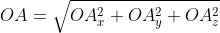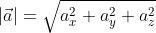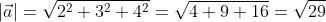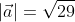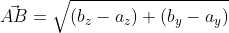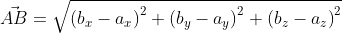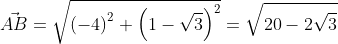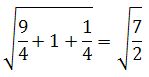Как найти длину отрезка ab вектор

Отрезок. Формула длины отрезка.

Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.

Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).

В данном примере вектор AB задан координатами (х₂— х₁, y₂— y₁). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:

Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек

Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х₁y₁) и (х₂,у₂).

Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.

Установим длину этих проекций.

На ось у длина проекции равна y₂ — y₁, а на ось х длина проекции равна х₂ — х₁. На основании теоремы Пифагора видим, что |AB|² = (y₂ – y₁)² + (x₂ – x₁)².

В рассмотренном случае |AB| выступает длиной отрезка.

Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.

Нахождение длины вектора, примеры и решения

Длина вектора — основные формулы

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

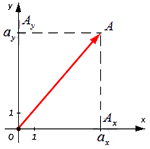
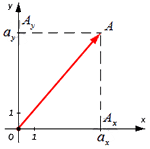
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e

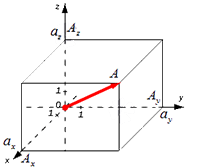
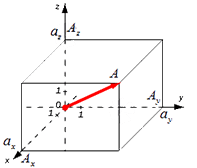
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.

Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2

А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .

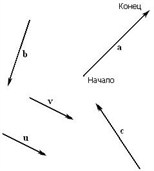
Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —

Ответ: A B → = 20 — 2 3 .

Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .

Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :

26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.

Длина вектора — основные формулы

Время чтения: 16 минут

Основные понятия вектора

Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.

Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».

Вектор — это отрезок с определённой длиной и направлением.

Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.

Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.

Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.

• Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
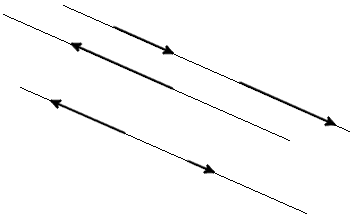
• Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.

• Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
• Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
• Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
  Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.

Как найти длину вектора

Модуль вектора а будем обозначать .

Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.

На взятой системе координат, от её начала отложим вектор
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.

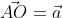
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует

Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 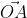получаем

Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор дан в формате разложения по координатным векторам , то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.

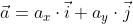
Чтобы рассчитать длину = (3, √x), расположенного в прямоугольной системе координат.

Чтобы найти модуль вектора используем ранее приведённую формулу

Ответ:

Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор =(aₓ ; aᵧ ; a )

В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому

из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:

Ответ:

Длина вектора через координаты точек начала и конца

Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.

Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле

При этом формула вычисления длины вектора для трёхмерного пространства, с координатами и ), будет следующей:

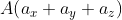
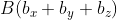
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)

Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:

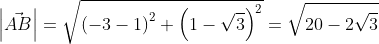
Существует второй вариант решения, где формулы применяются по очереди:

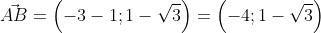
Ответ:

Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))

В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )

Длина вектора по теореме косинусов

Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.

К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.

Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).

В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)

Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.

длина вектора формула для трёхмерного пространства;

длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.

Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.

В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.

Применение векторов в других сферах

Понятие и вычисление вектора важно не только в математике, но и других науках:

• в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
• в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
• в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
• географии. Вектором обозначается движение воздушных масс, или течение реки;

Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.

источники:

http://zaochnik.com/spravochnik/matematika/vektory/dlina_vectora/

http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html

Вспомним для начала основные понятия и формулы.

Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.

Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:

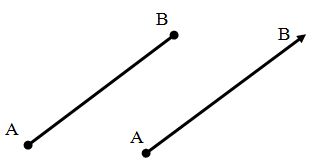
Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.

Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).

Замечу, что модулем вектора AB называется длина отрезка AB.

Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:

x = (x1 + x2)/2, y = (y1 + y2)/2.

До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.

Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).

Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:

А координаты середины отрезка AB найдем по формуле

x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.

И еще одна полезная формула: если вектор задан своими координатами, например,  MN(x1; x2; x3), то его модуль вычисляется по формуле:

Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,

(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).

Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,

5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).

Скалярным произведением двух векторов а и b называется число

a · b = |a»b| · сos (a, b),

Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:

MN · PK = x1 · y1 + x2 · y2 + x3 · y3.

Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).

Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.

Теперь давайте рассмотрим несколько задач на эту тему.

Задача 1.

Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.

Решение.

Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.

сos (a, b) = a · b/|a»b|.

Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.

Координаты векторов:

AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);

BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);

CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).

Модули:

|AB| =

|BC| =

|CA| =

Скалярные произведения:

AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;

BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;

AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.

Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как

сos (AB, CA) = AB · CA / |AB»CA| = 0.

А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.

Задача 2.

Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.

Решение.

Для начала найдем координаты точек M и N.

M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);

N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).

Теперь найдем координаты вектора MN:

MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).

Осталось найти модуль вектора MN.

|MN| =

Задача 3.

При каких значениях x векторы (x³ – 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?

Решение.

Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x³ – 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x³ – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.

Получим x € (-∞; 0) U (1; +∞).

Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x³ – 1) и 2x были различные знаки.

Задача 4.

Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.

Решение.

Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.

BC(7 – (-3); 7 – 1) = BC(10; 6);

AD(7 – 2; 1 – (-2)) = AD(5; 3).

Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.

Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Вектором является направленный отрезок. Длина этого отрезка является длиной вектора.

Длина вектора b⃗vec{b} обозначается ∣b⃗∣.left | vec{b} right |. Модуль числа имеет аналогичное обозначение и длина вектора часто называется модулем вектора.

Длина нулевого вектора равна нулю.

Нахождение длины вектора по его координатам

Длина вектора, который задан своими координатами, – это квадратный корень из суммы квадратов его координат.

Для того чтобы найти длину вектора, заданного своими координатами, нужно извлечь квадратный корень из суммы квадратов его координат.

1. Для вектора b⃗=(bx;by),vec{b}=(b_{x};b_{y}), заданного на плоскости, длина вычисляется по формуле ∣b⃗∣left |vec{b} right|=bx2+by2sqrt {b_{x}^{2}+b_{y}^{2}}.
2. Для вектора b⃗=(bx;by;bz),vec{b}=(b_{x};b_{y};b_{z}), заданного в пространстве, длина вычисляется по формуле ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}.

Пример 1

Найти длину вектора b⃗=(6;−4).vec{b}=(6;-4).

Вектор задан на плоскости, поэтому воспользуемся первой формулой: ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}}.

Подставим координаты вектора b⃗vec{b} в формулу, получим: ∣b⃗∣=62+(−4)2=36+16=52=213left | vec{b} right |=sqrt {6^{2}+(-4)^{2}}=sqrt {36+16}=sqrt {52}=2sqrt {13}.

Ответ: 2132sqrt {13}.

Пример 2

Найти длину вектора d⃗=(1;3;5).vec{d}=(1;3;5).

Вектор задан в пространстве, поэтому воспользуемся второй формулой:

∣d⃗∣=dx2+dy2+dz2left | vec{d} right |=sqrt {d_{x}^{2}+d_{y}^{2}+d_{z}^{2}}.

Подставим координаты вектора d⃗vec{d} в формулу, получим:

∣d⃗∣=12+32+52=1+9+25=35left | vec{d} right |=sqrt {1^{2}+3^{2}+5^{2}}=sqrt {1+9+25}=sqrt {35}.

Нахождение длины вектора по координатам точек его начала и конца

Для нахождения длины вектора CD⃗vec{CD}, где C(cx;cy)C(c_{x};c_{y}) и D(dx;dy)D(d_{x};d_{y}) существует определенная последовательность действий:

1. Найти координаты вектора CD⃗vec{CD} по формуле: ∣CD⃗∣=(dx−cx;dy−cy)left | vec{CD} right |=(d_{x}-c_{x};d_{y}-c_{y}).
2. Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}}.

Аналогично находится длина вектора CD⃗,vec{CD}, заданного в пространстве, где C(cx;cy;cz)C(c_{x};c_{y};c_{z}) и D(dx;dy;dz)D(d_{x};d_{y};d_{z}):

1. Найти координаты вектора CD⃗vec{CD} по формуле: CD⃗=(dx−cx;dy−cy;dz−cz).vec{CD}=(d_{x}-c_{x};d_{y}-c_{y};d_{z}-c_{z}).
2. Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2+(dz−cz)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}+(d_{z}-c_{z})^{2}}.

Пример 1

На плоскости заданы точки E(−1;3)иK(3;−4)E(-1;3) и K(3;-4). Найти длину вектора EK⃗.vec{EK}.

Найдем координаты вектора EK⃗.vec{EK}. Для этого из координат конца вычтем координаты начала, получим:

EK⃗=(3−(−1);−4−3)=(3+1;−4−3)=(4;−7).vec{EK}=(3-(-1);-4-3)=(3+1;-4-3)=(4;-7).

Воспользуемся формулой ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}} для нахождения длины вектора, получим:

∣EK⃗∣=42+(−7)2left | vec{EK} right |=sqrt {4^{2}+(-7)^{2}}=16+49sqrt {16+49}=65sqrt {65}.

Пример 2

В пространстве заданы точки C(1;2;3)C(1;2;3) и D(3;4;5).D(3;4;5). Найти длину вектора CD⃗.vec{CD}.

Найдем координаты вектора CD⃗.vec{CD}. Для этого из координат конца вычтем координаты начала, получим: CD⃗=(3−1;4−2;5−3)=(2;2;2).vec{CD}=(3-1;4-2;5-3)=(2;2;2).

Воспользуемся формулой ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}} для нахождения длины вектора, получим: ∣b⃗∣=22+22+22=4+4+4=12=23left | vec{b} right |=sqrt {2^{2}+2^{2}+2^{2}}=sqrt {4+4+4}=sqrt {12}=2sqrt 3.

Нахождение длины вектора по теореме косинусов

Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Для треугольника со сторонами a,b,ca, b, c и углами α,βalpha, beta и γ,gamma, противолежащими этим сторонам соответственно, справедливы равенства:

b=a2+c2−2a⋅c⋅cos(β),b=a^{2}+c^{2}-2acdot ccdot cos (beta), a=b2+c2−2b⋅c⋅cos(α),a=b^{2}+c^{2}-2bcdot ccdot cos (alpha), c=a2+b2−2a⋅b⋅cos(γ).c=a^{2}+b^{2}-2acdot bcdot cos (gamma).

Аналогично поступают и с векторами. Рассмотрим пример.

Пример 1

Длины векторов KL⃗vec{KL} и KM⃗vec{KM} равны соответственно 2 и 4, а угол между ними равен π4.frac{pi }{4}. Вычислите длину вектора LM⃗.vec{LM}.

Длина вектора LM⃗vec{LM} равна длине стороны LMLM в треугольнике LMKLMK. Также нам известны стороны KLKL и KMKM треугольника LMKLMK. Они равны длинам соответствующих векторов. Нам известен угол между векторами. Найдем сторону LMLM треугольника △KLM.triangle KLM.

LM2=KL2+KM2−2KL⋅KM⋅cos⁡∠LKM.LM^2=KL^2+KM^2-2KLcdot KMcdot cos angle LKM.
LM2=22+42−2⋅2⋅4⋅cos⁡π4=4+16−82=20−82.LM^2=2^2+4^2-2cdot 2cdot4cdot cos frac{pi }{4}=4+16-8sqrt{2}=20-8sqrt{2}.
LM=20−82.LM=sqrt{20-8sqrt{2}}.
∣LM⃗∣=20−82.|vec{LM}|=sqrt{20-8sqrt{2}}.

Тест по теме «Как вычислить длину вектора»

План урока:

Взаимосвязь координат векторов и его начала и конца

Определение координат середины отрезка

Вычисление длины вектора и отрезка

Простейшие задачи с использованием координатного метода

Использование признака коллинеарности векторов

Деление отрезка в заданном отношении

Введение прямоугольной системы координат

Взаимосвязь координат векторов и его начала и конца

На координатной плоскости любые две точки можно соединить друг с другом. В результате получается отрезок. Если же дополнительно указано, какая из этих точек – начало отрезка, а какая – конец, то в итоге мы уже имеем вектор. Попробуем определить, есть ли связь между координатами вектора и координатами (можно использовать сокращение коор-ты) его граничных точек.

Пусть в прямоугольной системе координат отмечены точки А (х_А;у_А) и В(х_B;у_B).Тогда можно задать вектор АВ. Также построим ещё два вспомогательных вектора ОА и ОВ, начинающиеся в точке О – начале коор-т:

Вектора ОВ и ОА – это радиус-векторы (так как их начало находится в начале координат), поэтому их коор-ты ОВ и ОА совпадают с коор-тами их концов (В и А соответственно):

Итак, зная коор-ты граничных точек вектора, можно найти и координаты данного вектора:

Например, если вектор начинается в точке А (2; 1), а заканчивается в точке В (6; 3), то коор-ты вектора АВ можно определить так:

Задание. Начало вектора находится в точке М, а конец – в точке К. Определите его коор-ты, если:

а) М(2; 7) и К(6; 8);

б) М(5; 1) и К(2; 10);

в) М(0; и К(9; -5).

Решение. Из коор-т К мы просто вычитаем соответствующие коор-ты М, и в итоге определяем коор-ты вектора:

Задание. От точки H (8; 15) отложили вектор m{5; – 6}. Каковы координаты конца этого вектора?

Решение. Обозначим интересующие нас коор-ты как (х_к; у_к). Для вектора, начинающегося в точке (8; 15) и заканчивающегося в точке (х_к; у_к), коор-ты можно вычислить так:

x = x_k — 8

y = y_k — 15

Однако нам даны координаты вектора, то есть величины х и у, поэтому мы можем записать:

5 = x_k — 8

-6 = y_k — 15

Оба равенства представляет собой уравнения, которые можно решить:

5 = x_k — 8

x_k = 5 + 8 = 13

-6 = y_k — 15

y_k = -6 + 15 = 9

В итоге получили, что конец вектора находится в точке (13; 9).

Ответ:(13; 9).

Определение координат середины отрезка

Пусть построен вектор АВ, причем известны коор-ты его начала А (х_А; у_А) и его конца B (х_B; у_B). Обозначим буквой С середину отрезка АВ и попытаемся вычислить коор-ты С, которые мы обозначим как (х_C; у_C):

Рассмотрим вектора АС и СВ. Они имеют одинаковую длину, потому что С разбивает АВ пополам. Также АС и СВ коллинеарны, так как они лежат на одной прямой АВ. При этом они и сонаправлены, а значит, эти вектора равны:

Нам удалось выразить коор-ты С через координаты А и В. В итоге можно сформулировать правило:

Например, пусть необходимо найти координаты середины отрезка HK, при этом известны коор-ты его концов: Н(5; – 2) и К(3; 4). Сначала найдем полусумму коор-т х и получим эту же коор-ту у середины:

Итак, точка середины отрезка имеет коор-ты (4; 1). Для наглядности построим отрезок ОК и продемонстрируем, что его середина действительно находится в точке (4; 1):

Вычисление длины вектора и отрезка

Пусть есть произвольный вектор с коор-тами {x; у}. Отложим его от точки начала координат, после чего из его конца опустим перпендикуляры ОВ и ОС на координатные оси:

Для простоты рассмотрим случай, когда х и у – положительные числа, то есть точка А находится в первой четверти. Тогда длина ОВ будет равна х:

OB = x

Так как ОСАВ – прямоугольник, то стороны ОС и АВ одинаковы, причем ОС имеет длину, равную коор-те у:

AB = OC = y

Теперь изучим ∆ОВА. Он прямоугольный, и ОА в нем – гипотенуза, поэтому можно записать теорему Пифагора:

OA² = OB² + AB²

Теперь заменим отрезки ОВ и АВ на х и у:

OA² = x² + y²

Осталось извлечь квадратный корень:

Мы вывели формулу для вычисления длины вектора по его координатам. Можно рассмотреть и остальные случаи, когда точка А лежит в другой четверти координатной плоскости или на координатных осях, однако во всех случаях будет получаться одинаковая формула.

Задание. Определите длину вектора с коор-тами:

Решение. Во всех случаях просто возводим каждую коор-ту в квадрат, потом складываем полученные числа и извлекаем из полученной суммы квадратный корень:

Теперь предположим, что имеется две точки с коор-тами (х₁; у₁) и (х₂; у₂). Требуется найти длину отрезка, их соединяющего, то есть расстояние между этими двумя точками. Если принять одну из этих точек, например первую, за начало вектора, а вторую за его конец, то задача сведется к вычислению длины этого вектора. Его коор-ты можно будет высчитать так:

x = x₂ — x₁

y = y₂ — y₁

Тогда расстояние между точками (обозначим его как d) будет вычисляться по формуле:

Задание. Определите длину отрезка MP, если известны коор-ты его концов:

Простейшие задачи с использованием координатного метода

Выведенные нами формулы являются базовыми для расчетов, связанных с коор-тами. До этого мы решали лишь простейшие задачи на использование этих формул, однако в более сложных задачах надо использовать сразу несколько более сложных формул.

Задание. Известны коор-ты трех вершин параллелограмма АВСD: А(4; 1), В(1; 1), С(3; 5). Определите коор-ты четвертой вершины D.

Решение.

Сначала найдем коор-ты вектора ВС. Мы можем это сделать, так как нам известны коор-ты его начальной и конечной точки:

x_BC = x_C — x_B = 3 — 1 = 2

y_BC = y_C — y_B = 5 — 1 = 4

Так как в параллелограмме противоположные стороны имеют одинаковую длину и при этом параллельны, то вектора ВС и АD равны, то есть имеют одинаковые коор-ты:

Итак, D имеет коор-ты (6; 5).

Ответ (6; 5).

Задание. В – середина отрезка АС. Известны коор-ты точек: А(2; 4) и В(0; 18). Найдите коор-ты С.

Решение.

Для начала будем работать только с коор-той х. Так как В – середина АС, то их абсциссы (напомним, так называют координату х точек) связаны соотношением:

Задание. Отрезок MN имеет длину 13. Даны координаты концов отрезка: M(4; 6) и N (х; 1). Найдите величину переменной х.

Нам по условию известно это расстояние для точек M и N, а также известны 3 и 4 коор-т точек. Поэтому надо просто подставить все известные данные в формулу, получить уравнение и решить его:

Далее извлекаем корень из обеих частей, но при этом появляется два различных корня (так обычно и бывает при решении квадратных уравнений):

Ответ: – 8 или 16.

Задание. Расстояние от точки S(2x; – 2) до точки T (6; 4х) составляет 14. Определите величину х.

Решение. Задача во многом аналогично предыдущей, надо подставить в формулу расстояния между точками данные из условия и решить получившееся уравнение:

Решаем это квадратное уравнение через дискриминант:

Ответ: (– 2,6) или 3.

Задание. Найдите коор-ты точки M на рисунке, если точка А имеет коор-ты (4; 2).

Решение. По рисунку видно, что середина отрезка находится в точке О(0; 0). Коор-ты середины отрезка (то есть точки О) и его граничных точек связаны формулами:

Использование признака коллинеарности векторов

На прошлом уроке мы выяснили, что если вектора коллинеарны, то их коор-ты пропорциональны. Это позволяет определить, лежит ли та или иная точка на указанной прямой.

Задание. Даны точки А(1; 2), В(4; 7) и С (10; 17). Определите, лежит ли точка В на прямой АС.

Решение. Если А, В и С принадлежат одной прямой, то любые два вектора, проведенные через эти точки, окажутся коллинеарными друг другу. Если же они НЕ лежат на одной прямой, то наоборот, любые два таких вектора окажутся неколлинеарными. То есть надо составить два вектора, например, АВ и ВС, и проверить их коллинеарность.

Определим коор-ты АВ:

Напомним, что для проверки векторов на коллинеарность надо поделить их коор-ты друг на друга. Если получится одно и то же число, то вектора коллинеарны:

В обоих случаях получилось одинаковое число, значит, вектора коллинеарны.

Ответ: Да, точка B лежит на прямой AC.

Задание. Проверьте, лежат ли точки А(3; 7), В (8; 12) и С(6; 4) на одной прямой.

Решение. Снова вычисляем коор-ты векторов АВ и ВС:

Получились разные числа, следовательно, вектора АВ и ВС не коллинеарны, а потому точки А, В и С никак не могут лежать на одной прямой.

Ответ: Нет, точки A,B,C не лежат на одной прямой.

Задание. Проверьте, параллельны ли друг другу отрезки АВ и CD, если известны коор-ты: А(1; 1), В(5; 5), С(4; 2), D(6; 4).

Решение. Если отрезки параллельны, то и вектора АВ и CD должны быть коллинеарными. Проверим это также, как мы это делали в двух предыдущих задачах:

Итак, вектора коллинеарны. Означает ли это, что отрезки АВ и CD параллельны? Ещё нет. На самом деле возможно два случая:

1) АВ и CD действительно параллельны;

2) АВ и СD лежат на одной прямой, и тогда их параллельными считать нельзя.

Как же проверить, какой из двух случаев относится к этой задаче? Надо рассмотреть ещё один ВС. Если реализуется второй случай, то он окажется коллинеарен вектору АВ. В первом же случае он будет ему не коллинеарен.

Получили различные числа, значит, АВ и ВС не коллинеарны. Теперь мы можем точно утверждать, что АВ и СD параллельны.

Ответ: Да, отрезки AB и CD параллельны.

Деление отрезка в заданном отношении

Мы уже научились находить коор-ты середины отрезка. Можно сказать, что середина – это точка, которая разбивает отрезок в отношении 1:1, то есть на равные отрезки. А что делать в более сложном случае, если нужно найти точку, разбивающую отрезок в другом отношении, например, в отношении 2:1? Выведем для такого случая формулу.

Пусть точка С разбивает отрезок АВ в некотором отношении так, что отрезок АС в k больше отрезка СВ:

(Примечание. Если отрезок АС меньше СВ, то число k будет меньше единицы.)

Как и обычно, для обозначения коор-т точек используем индексы, совпадающие с обозначением точек: А(x_А; у_А), В(x_В; у_В) и С(x_С; у_С).

Нам также потребуются вектора АС{x_АС; у_АС} и СВ{x_СВ; у_СВ}. Так как эти вектора сонаправлены, и АС в k раз длиннее, то

Абсолютно аналогичные образования приведут к такому же выражению для коор-ты у:

Рассмотрим на примерах использование этой формулы.

Задание. На отрезке РM отложена точка K так, что она разбивает РM на отрезки РK и KM в отношении РK:KM = 2:1. Даны коор-ты точек: Р(6; 3) и К (18; 12). Вычислите коор-ты K.

Решение.

Отношение РК:КМ = 2:1 означает, что отрезок РК в 2 раза длиннее, чем КМ. Это означает, что в формуле

Задание. Точки B (5; – 16) и H(29; 24) соединены отрезком. Точка M на отрезке ВН отмечена так, что ВМ:МН = 3:5. Определите коор-ты точки М.

Решение. Из отношения ВМ:МН = 3:5 вытекает, что ВМ длиннее МН в

3/5 = 0,6 раз

то есть фактически ВМ короче МН. То есть при использовании формулы

Рассмотрим ещё несколько более усложненных задач с использованием коор-т.

Задание. Точка K лежит на оси Ох, при этом она равноудалена от точек Е(2; 2) и F(6; 10). Найдите коор-ты К.

Решение. У любой точки, лежащей на оси Ох, коор-та у будет равна нулю, в том числе и у точки К:

y_k = 0

Будем обозначать неизвестную коор-ту К как х:

x_k = x

Напомним расстояние между точками можно рассчитать, используя формулу:

Получили иррациональное уравнение. В данном случае можно просто приравнять подкоренные выражения, однако после получения корней надо проверить, нет ли среди них посторонних:

Проверяем, не является ли корень посторонним. Для этого просто подставляем его в уравнение:

Корень действительно подошел, поэтому коор-та х точки К равна 16.

Ответ: (16; 0).

Введение прямоугольной системы координат

Даже если в формулировке задачи коор-ты и вектора прямо не упоминаются, может быть полезным самостоятельно добавить в нее прямоугольную систему координат. Это позволит использовать формулы, используемые в методе коор-т, для решения задачи.

Задание. Докажите, что если в параллелограмме сложить квадраты всех его сторон, то получится то же число, что и при сложении квадратов диагоналей этого параллелограмма.

Решение. Расположим систему коор-т таким образом, одна из сторон параллелограмма находилась на оси Ох, причем одна ее вершина совпадала с началом коор-т, а другая имела положительную коор-ту х:

Пусть вершина А находится в начале коор-т, и тогда она имеет коор-ты (0; 0). Вершина D лежит на Ох, тогда ее ордината равна нулю, а абсциссу обозначим буквой а. Точка В имеет произвольные коор-ты (b; с), коор-ты же точки С можно рассчитать. Сначала заметим, что вектор коор-ты вектора АВ совпадают с коор-тами точки В, так как он является радиус-вектором:

Вектора АВ и DC равны, потому что они лежат на параллельных прямых и имеют одинаковую длину:

Итак, коор-ты С – это (а + b; с).

Теперь мы должны длину каждой стороны параллелограмма и возвести ее в квадрат. Обратите внимание, что если расстояние между точками рассчитывается по формуле

Равенство доказано.

Задание. В равнобедренном треугольнике длина основания составляет 80 см, а опущенная на нее медиана имеет длину 160 см. Вычислите длины двух других медиан.

Решение. Пусть АВС – рассматриваемый в задаче треугольник, причем АВ – его основание. Расположим систему коор-т так, чтобы ее начало совпадало с точкой, в которой медиана пересекается с основанием:

В этом случае вершина, из которой опущена медиана, будет иметь коор-ты (0; 160), а две другие вершины будут иметь коор-ты (– 40; 0) и (40; 0).

Нам надо найти длину двух других медиан АM и BN. Они одинаковы по длине, поэтому достаточно найти длину только одной из них, например, АМ. Для этого сначала найдем коор-ты М, которая является серединой ВС:

Сегодня мы познакомились с важнейшими формулами, используемыми в методе коор-т, и научились решать некоторые простейшие задачи. В будущем мы узнаем о более сложных задачах, в которых будут фигурировать не только отрезки и многоугольники, но и окружности.

© 2011-2023 Довжик Михаил
Копирование материалов запрещено.

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com