Как найти длину отрезка через уравнение - Исправление недочетов и поиск решений вместе с Examum.ru

Отрезок. Формула длины отрезка.

Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.

Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).

В данном примере вектор AB задан координатами (х₂— х₁, y₂— y₁). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:

Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек

Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х₁y₁) и (х₂,у₂).

Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.

Установим длину этих проекций.

На ось у длина проекции равна y₂ — y₁, а на ось х длина проекции равна х₂ — х₁. На основании теоремы Пифагора видим, что |AB|² = (y₂ – y₁)² + (x₂ – x₁)².

В рассмотренном случае |AB| выступает длиной отрезка.

Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.

Длина отрезка. Расстояние между точками: онлайн-калькулятор

Чтобы найти расстояние между точками (длину отрезка) онлайн, необходимо:

Задать размерность (плоскость или пространство).
Ввести в поля координаты точек.
Нажать «рассчитать».

Как найти длину отрезка (расстояние между точками) с помощью онлайн-калькулятора

Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Найдем длину произвольного отрезка, начальная и конечная точки которого имеют координаты (1;4) и (3;0). Для этого:

Выберем размерность (2 или 3). Калькулятор позволяет задать отрезок соответственно на плоскости, или в пространстве. В нашем конкретном примере выберем плоскость (2):
Введем в пустые поля координаты начальной и конечной точек отрезка:
После ввода координат остается нажать «Рассчитать» и получить ответ с решением:

Длина отрезка

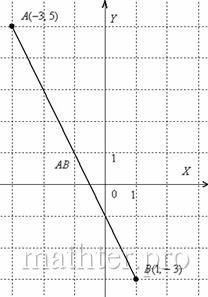
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)². В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.

Рассчитаем длину отрезка А, для этого найдем квадратный корень:

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.

источники:

http://zaochnik.com/online-calculators/tochka-pryamaya-ploskost/dlina-otrezka-rasstoyanie-mezhdu-tochkami/

http://studyguide.ru/note.php?id=14

Источник

Длина, как уже отмечалось, обозначается знаком модуля.

Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле:

Если даны две точки пространства и , то длину отрезка можно вычислить по формуле:

Примечание: соответствующие координаты можно переставить местами: и ,

но это нестандартный вариант.

Задача 3

Даны точки и . Найти длину отрезка .

Решение: по соответствующей формуле:

Ответ: (единицы)

Обратите внимание на вынесение множителя из-под корня: (см. Приложение Школьные материалы). Это крайне

желательное действие, если оно возможно. Ибо будет придирка со стороны преподавателя. С высокой вероятностью.

И для наглядности снова выполню чертёж, тут есть что сказать:

Отрезок – это не вектор, а обычный ненаправленный

отрезок. И перемещать его куда-либо, конечно, нельзя.

Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину

отрезка . Но проще, конечно, использовать Калькулятор (приложен к книге).

Кстати, в ответе не забываем указать размерность: «единицы». В условии не сказано, ЧТО это – миллиметры, сантиметры, метры

или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».

Задание для самостоятельного решения с отрезком в пространстве:

Задача 4

Даны точки и . Найти длину отрезка .

Решение и ответ в конце книги.

1.5.3. Как найти длину вектора?

1.5.1. Как найти вектор по двум точкам?

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Загрузить PDF

Найти длину вертикального или горизонтального отрезка на координатной плоскости можно с помощью координат, а вот сделать это с диагональным отрезком сложнее. Длину диагонального отрезка можно вычислить по формуле, которая основана на теореме Пифагора, где гипотенузой прямоугольного треугольника является наш диагональный отрезок.^[1] С помощью этой формулы можно быстро найти длину любого отрезка на координатной плоскости.

1

Запишите формулу для вычисления длины. Формула: $d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}$ , где — длина отрезка, $(x_{{1}},y_{{1}})$ — координаты начальной точки отрезка, $(x_{{2}},y_{{2}})$ — координаты конечной точки отрезка.^[2]
2

Найдите координаты точек отрезка. Возможно, они будут даны. Если нет, найдите их по осям Х и Y.^[3]
3

Подставьте координаты в формулу. Будьте внимательны и подставьте значения соответствующих переменных. Две координаты должны находится внутри первой пары скобок, а две координаты — внутри второй пары скобок.^[4]

Реклама

1

Выполните вычитание в скобках. Сделайте это, потому что операции в скобках имеют приоритет.^[5]
2

Возведите в квадрат полученные значения. В нашем случае возведение в степень — это вторая по важности операция.^[6]
3

Сложите числа под знаком корня. Делайте вычисления так, как будто работаете с целыми числами.
4

Вычислите длину отрезка . Для этого извлеките корень из полученной суммы чисел.

Реклама

Советы

Не путайте эту формулу с другими, например, с формулой для вычисления углового коэффициента или с линейным уравнением.
Помните о порядке выполнения математических операций. Сначала вычтите, затем возведите в квадрат, затем сложите, а затем извлеките квадратный корень.

Об этой статье

Эту страницу просматривали 24 709 раз.

Была ли эта статья полезной?

Источник

Онлайн калькулятор. Длина отрезка. Расстояние между точками.

Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния между точками.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния между точками и закрепить пройденный материал.

Калькулятор для вычисления расстояния между двумя точками

Выберите необходимую вам размерность:

Размерность:

Введите координаты точек.

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Нестандартные графики. Уравнение отрезка

Задание
1

#6713

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases}
sqrt{(x+2)^2+y^2}+sqrt{x^2+(y-a)^2}=sqrt{4+a^2}\
5y=|6-a^2|
end{cases}]

имеет единственное решение.

(Задача от подписчиков)

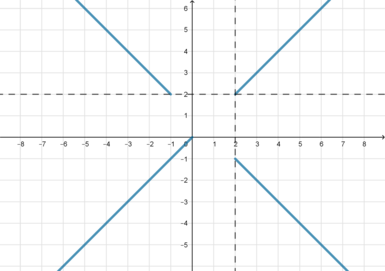
Рассмотрим второе уравнение системы: оно задает семейство прямых (y=0,2|6-a^2|), параллельных оси (Ox) и лежащих в верхней полуплоскости (включая ось (Ox)) при любом значении параметра (a) (т.к. модуль всегда неотрицателен).

Рассмотрим первое уравнение. Пусть (A(x;y)), (B(-2;0)), (C(0;a)) – точки. Тогда (BA=sqrt{(x+2)^2+y^2}), (AC=sqrt{x^2+(y-a)^2}), (BC=sqrt{4+a^2}).
Таким образом, первое уравнение системы выглядит так: (BA+AC=BC). Значит, оно задает геометрическое место точек (A), лежащих на отрезке (BC).

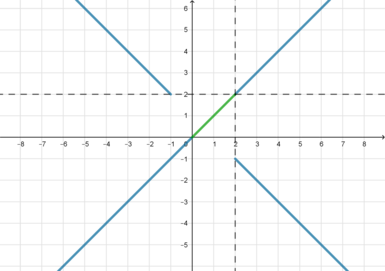
Для того, чтобы данная система имела единственное решение, прямая (y=0,2|6-a^2|) должна пересекать отрезок (BC) в одной точке.

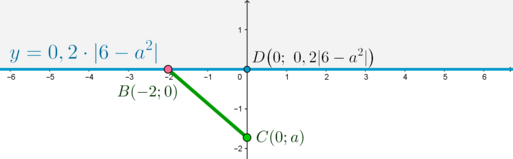
1) Пусть (a<0), то есть точка (C) лежит на отрицательной части оси (Oy). Единственный случай, когда прямая (y=0,2|6-a^2|) будет иметь с отрезком одну общую точку, – когда прямая (y=0,2|6-a^2|) будет проходить через точку (B), то есть совпадать с осью абсцисс. Отсюда (0,2|6-a^2|=0), следовательно, (a=pm sqrt6). Так как (a<0), то (a=-sqrt6).

2) Пусть (a=0). Тогда отрезок (BC) лежит на оси абсцисс, прямая (y=0,2|6-a^2|) – в верхней полуплоскости, и общих точек у них нет.

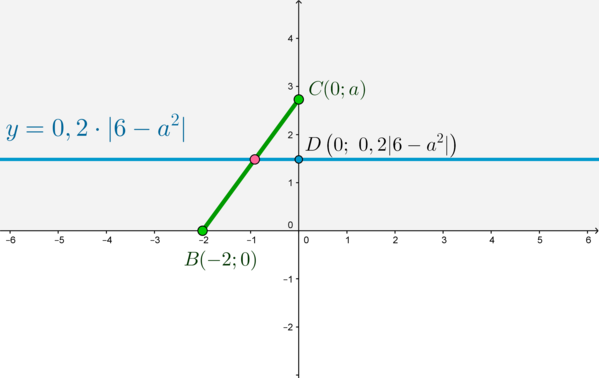
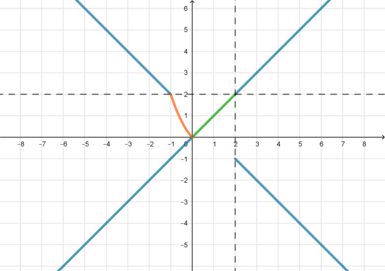
3) Пусть (a>0). Тогда (C) лежит на положительном направлении оси ординат.

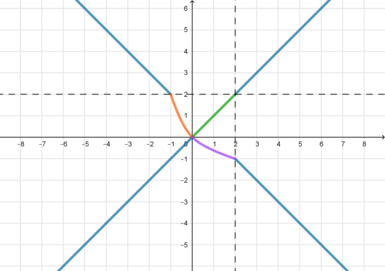
Прямая (y=0,2|6-a^2|) пересекает ось ординат в точке (D). Для того, чтобы прямая пересекала отрезок (BC), нужно, чтобы точка (C) находилась не ниже точки (D), то есть [ageqslant 0,2|6-a^2|]

Решим данное неравенство. Т.к. (a>0), то имеем: [|6-a^2|leqslant
5aquadLeftrightarrowquad -5aleqslant 6-a^2leqslant
5aquadLeftrightarrowquad 1leqslant aleqslant 6.]

Ответ:

(ain{-sqrt6}cup[1;6])

Задание
2

#3978

Уровень задания: Равен ЕГЭ

Найдите все значения параметра (a), при каждом из которых система [begin{cases}
y^2-(2a+1)y+a^2+a-2=0\
sqrt{(x-a)^2+y^2}+sqrt{(x-a)^2+(y-3)^2}=3 end{cases}] имеет ровно одно решение.

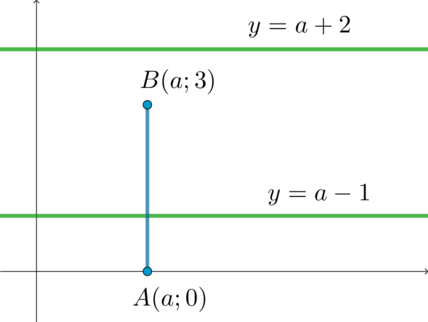
Преобразуем первое уравнение системы. Заметим, что (a^2+a-2=(a+2)(a-1)). Заметим также, что (a+2+a-1=2a+1), следовательно, по теореме Виета корнями этого уравнения будут (y=a+2) и (y=a-1). Значит, графиком первого уравнения будут две прямые (y=a+2) и (y=a-1), параллельные оси абсцисс.

Преобразуем второе уравнение. Рассмотрим точки (A(a;0)), (B(a;3)), (C(x;y)). Тогда (AB=sqrt{(a-a)^2+(0-3)^2}=3), (AC=sqrt{(x-a)^2+y^2}) и (CB=sqrt{(x-a)^2+(y-3)^2}). Следовательно, второе уравнение системы можно переписать в виде (AC+CB=AB). Значит, оно задает множество точек (C), которые лежат на отрезке (AB). Заметим, что так как у точек (A) и (B) абсцисса одинаковая, то отрезок (AB) перпендикулярен оси абсцисс.

Схематично графики обоих уравнений выглядят так:
Чтобы система имела единственное решение, нужно, чтобы зеленый график пересекал отрезок (AB) в одной точке. Следовательно, либо прямая (y=a+2) пересекает отрезок, а прямая (y=a-1) его не пересекает, либо наоборот: [left[begin{gathered}begin{aligned}
&begin{cases} 0leqslant a+2leqslant 3\
a-1<0 end{cases} \
&begin{cases} 0leqslant a-1leqslant 3\
a+2>3end{cases}
end{aligned}end{gathered}right.quadLeftrightarrowquad
ain [-2;1)cup(1;4]]

Ответ:

([-2;1)cup(1;4])

Задание
3

#3979

Уровень задания: Равен ЕГЭ

Найдите наименьшее значение параметра (a), при котором уравнение [sqrt{(x+8)^2+(x+2)^2}+sqrt{(x+14)^2+(x+3)^2}=13a] имеет хотя бы один корень.

1 способ.

Рассмотрим (f(x)=sqrt{(x+8)^2+(x+2)^2}+sqrt{(x+14)^2+(x+3)^2}).
Тогда уравнение примет вид (f(x)=13a). Тогда нам нужно найти наименьшее значение (a), при котором прямая (y=13a) будет пересекать график (y=f(x)) хотя бы в одной точке. Исследуем (f(x)). Для этого найдем сначала ее производную: [begin{aligned}
&f'(x)=dfrac{2(x+8)+2(x+2)}{2sqrt{(x+8)^2+(x+2)^2}}+
dfrac{2(x+14)+2(x+3)}{2sqrt{(x+14)^2+(x+3)^2}}=\[2ex]
&=dfrac{2x+10}{sqrt{(x+8)^2+(x+2)^2}}+
dfrac{2x+17}{sqrt{(x+14)^2+(x+3)^2}} end{aligned}] Найдем нули производной: [begin{aligned}
&dfrac{2x+10}{sqrt{(x+8)^2+(x+2)^2}}+
dfrac{2x+17}{sqrt{(x+14)^2+(x+3)^2}}=0 quadLeftrightarrow\[2ex]
&sqrt{dfrac{(x+14)^2+(x+3)^2}{(x+8)^2+(x+2)^2}}=-dfrac{2x+17}{2x+10}
quadLeftrightarrow\[2ex]
&begin{cases}
dfrac{(x+14)^2+(x+3)^2}{(x+8)^2+(x+2)^2}=left(dfrac{2x+17}{2x+10}right)^2
qquad (*)\[2ex]
dfrac{2x+17}{2x+10}leqslant 0end{cases}
quadLeftrightarrow\[2ex]
&begin{cases} 85x^2+598x+424=0\
xin left[-8,5; -5right) end{cases}
quadLeftrightarrow\[2ex]
& x=-dfrac{106}{17}
end{aligned}]

Определим знаки производной:

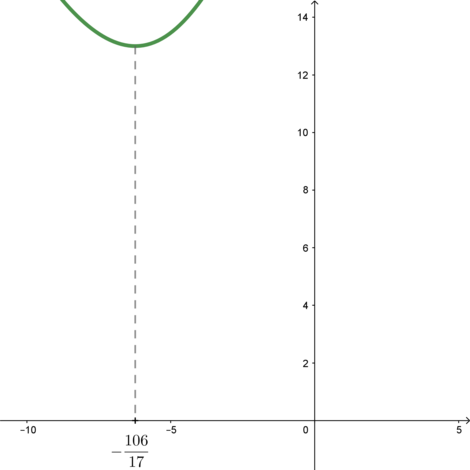
Следовательно, схематично график функции выглядит так:

Следовательно, наименьшее значение параметра (a) – когда прямая (y=13a) проходит через точку экстремума функции (f(x)): [13a=fleft(-dfrac{106}{17}right)quadLeftrightarrowquad
13a=13quadLeftrightarrowquad a=1]

2 способ.

Заметим, что в первом способе было очень много вычислений и на самом деле нам повезло, что при решении уравнения ((*)) слагаемые с (x^4) и (x^3) взаимно уничтожились и мы пришли к квадратному уравнению. А что делать, если числа так хорошо не подобраны и мы не получим в конечном итоге “красивое” уравнение, которое сможем решить?
Давайте рассмотрим второй способ решения подобных уравнений.

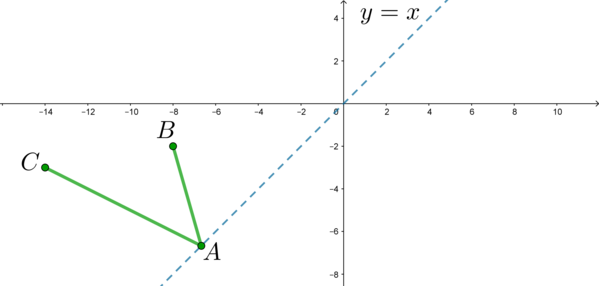
Рассмотрим три точки: (A(x;x)), (B(-8; -2)), (C(-14; -3)). Тогда уравнение примет вид [AB+AC=13a] Если нам нужно найти наименьшее значение параметра (a), при котором уравнение имеет хотя бы одно решение, то нам нужно найти точку (A), при которой сумма длин отрезков (AB) и (AC) будет наименьшей.
Где располагается точка (A)? Эта точка “бегает” по прямой (y=x). Графически это выглядит так:

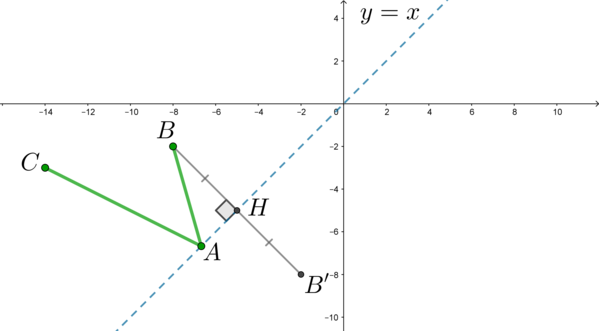
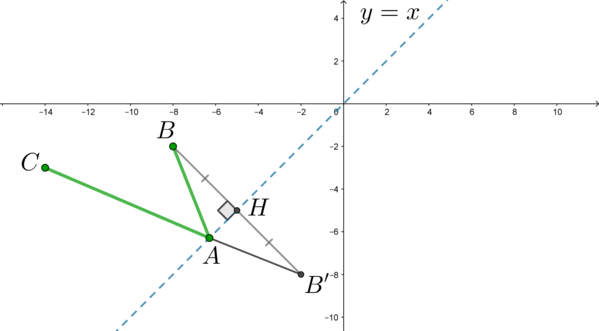
Здесь мы будем использовать классическую идею планиметрии. Отразим симметрично точку (B) относительно прямой (y=x) (то есть проведем (BB’perp y=x), где (BH=HB’):

Тогда (AB+AC=AB’+AC). Заметим, что по правилу треугольника, если точка (A) не лежит на отрезке (B’C), то (AB’+AC>B’C). Следовательно, наименьшая сумма длин (AB’+AC) будет достигаться тогда, когда (Ain
B’C).

Таким образом, мы идейно поняли, где должна находиться точка (A). Теперь осталось найти ее координаты.

1) Найдем координаты точки (B’).
Для этого сначала найдем уравнение прямой (BB’). Так как (BB’perp
y=x), то если уравнение прямой (BB’) имеет вид (y=kx+b), то (kcdot
1=-1) (произведение угловых коэффициентов двух взаимно перпендикулярных прямых равно (-1)). Следовательно, (y=-x+b).
Для того, чтобы найти число (b), нужно подставить координаты точки (B) в уравнение прямой: [-2=-1cdot (-8)+bquadLeftrightarrowquad b=-10] Следовательно, уравнение прямой имеет вид (y=-x-10).
Найдем координаты точки (H) – это точка пересечения прямых (y=x) и (y=-x-10): [begin{cases} y=x\ y=-x-10end{cases}quadLeftrightarrowquad
x=y=-5quadRightarrowquad H(-5;-5)] (H) – середина отрезка (BB’). Значит, если координаты точки (B’) равны ((x_0;y_0)), то [begin{cases}
-5=dfrac{-8+x_0}2\[2ex]
-5=dfrac{-2+y_0}2end{cases}quadLeftrightarrowquad
begin{cases}
x_0=-2\
y_0=-8end{cases}] Таким образом, (B'(-2;-8)).

2) Найдем уравнение прямой (B’C). Если уравнение этой прямой в общем виде выглядит как (y=mx+n), то [begin{cases}
-8=-2m+n\
-3=-14m+nend{cases}quadLeftrightarrowquad begin{cases}
m=-dfrac5{12}\[2ex] n=-dfrac{53}6end{cases}] Следовательно, (y=-frac5{12}x-frac{53}6). Теперь можно найти координаты точки (A) – это точка пересечения прямых (y=x) и (B’C): [begin{cases}
y=x\[2ex] y=-frac5{12}x-frac{53}6end{cases}
quadLeftrightarrowquad x=y=-dfrac{106}{17}]

3) Теперь можно найти значение параметра (a). [13a=AB’+AC=13quadRightarrowquad a=1]

Чем хорош этот способ? Во-первых, он более изящный. Во-вторых, в ходе решения мы сталкивались только с линейными уравнениями, которые решать намного проще.

Ответ:

(a=1)

Задание
4

#3909

Уровень задания: Сложнее ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases}
x^2+|x^2-2x|=y^2+|y^2-2y|\
x+y=aend{cases}]

имеет более двух решений.

Изобразим график первого уравнения. Для этого рассмотрим случаи:

1) (x^2-2xgeqslant 0), (y^2-2ygeqslant 0). Тогда уравнение примет вид [x^2+x^2-2x=y^2+y^2-2yquadLeftrightarrowquad
x^2-y^2-(x-y)=0quadLeftrightarrowquad
(x-y)(x+y-1)=0quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &y=x\
&y=1-xend{aligned}end{gathered}right.] Тогда в этом случае получаем такой график:

2) (x^2-2xleqslant 0), (y^2-2yleqslant 0). Тогда: [x^2+2x-x^2=y^2+2y-y^2quadLeftrightarrowquad y=x] Значит, график для первых двух случаев будет выглядеть уже так:

3) (x^2-2xgeqslant 0), (y^2-2yleqslant 0). Тогда уравнение примет вид: [x^2+x^2-2x=y^2-y^2+2yquadLeftrightarrowquad y=x^2-x] Следовательно, добавится еще:

4) (x^2-2xleqslant 0), (y^2-2ygeqslant 0). Тогда имеем: [x=y^2-y] Графиком будет являться такая же парабола, как и в п.3, только с поменявшимися осями:

Графиком (x+y=a) при каждом фиксированном (a) является прямая (y=-x+a), то есть прямая, параллельная (y=-x) (а также параллельная части прямой (y=1-x) из п. 1).
Для того, чтобы система имела более двух решений, нужно, чтобы прямая (y=-x+a) находилась в положениях от (1) (не включительно) до (2) (включительно):

Действительно, когда прямая находится в положении (2), то система будет иметь бесконечное множество решений (а именно, часть прямой (y=1-x) при (xin (-infty;-1]cup[2;+infty)), а также точка ((0,5;0,5))); когда прямая находится между (1) и (2), то система будет иметь 3 решения; когда прямая находится в положении (1), то система будет иметь одно решение: (x=0, y=0).
Прямая (y=-x+a) находится в положении (1) при (a=0), в положении (2) – при (a=1), следовательно, [ain (0;1]]

Ответ:

(ain (0;1])

Задание
5

#3908

Уровень задания: Сложнее ЕГЭ

Найдите все значения параметра (a), при которых система [begin{cases}
|x^2-1|+2x-x^2=|y^2-1|+2y-y^2\
x+y=aend{cases}]

имеет более двух решений.

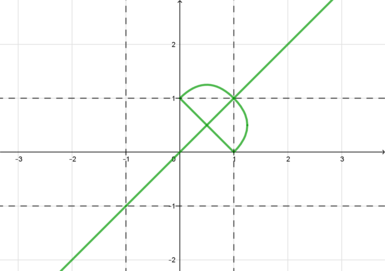
Изобразим график первого уравнения. Для этого рассмотрим следующие случаи:

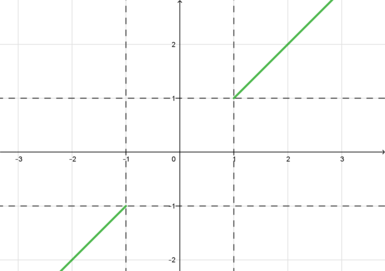
1) (x^2-1geqslant 0), (y^2-1geqslant 0). Тогда уравнение примет вид [x^2-1+2x-x^2=y^2-1+2y-y^2quadLeftrightarrowquad x=y] Следовательно, в части плоскости, задающейся условиями (|x|geqslant
1), (|y|geqslant 1), графиком будет часть прямой (y=x):

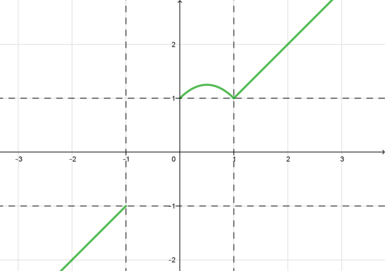
2) (x^2-1leqslant 0), (y^2-1geqslant 0). Тогда уравнение примет вид: [1-x^2+2x-x^2=y^2-1+2y-y^2quadLeftrightarrowquad y=-x^2+x+1] Следовательно, в части плоскости, задающейся условиями (|x|leqslant
1, |y|geqslant 1), графиком будет часть параболы (y=-x^2+x+1):

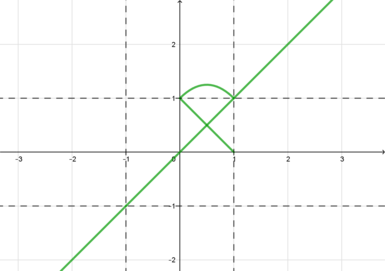
3) (x^2-1leqslant 0), (y^2-1leqslant 0): [1-x^2+2x-x^2=1-y^2+2y-y^2quadLeftrightarrowquad
1-2y+y^2-x^2=1-2x+x^2-y^2quadLeftrightarrowquad
(1-y)^2-x^2=(1-x)^2-y^2quadLeftrightarrow] [Leftrightarrowquad
(1-y-x)(1-y+x)=(1-x-y)(1-x+y)quadLeftrightarrowquad
(1-y-x)(1-y+x-1+x-y)=0quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &y=1-x\
&y=xend{aligned}end{gathered}right.] Следовательно, добавится еще такой кусок графика:

4) (x^2-1geqslant 0), (y^2-1leqslant 0). Тогда имеем [x=-y^2+y+1] Графиком будет та же парабола, что и в п. 2, если поменять оси местами.

Таким образом, окончательный график первого уравнения будет выглядеть так:

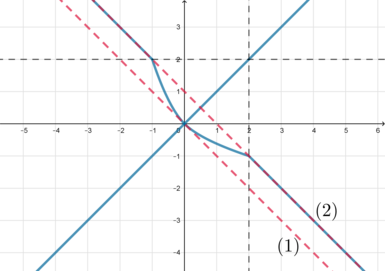
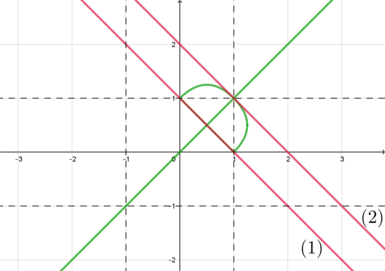
Графиком (x+y=a) при каждом фиксированном (a) является прямая (y=-x+a), то есть прямая, параллельная (y=-x) (а также параллельная части прямой (y=1-x) из п. 3).
Для того, чтобы система имела более двух решений, нужно, чтобы прямая (y=-x+a) находилась в положениях от (1) (включительно) до (2) (не включительно):

Действительно, когда прямая находится в положении (1), то система будет иметь бесконечное множество решений (а именно, часть прямой (y=1-x) при (xin [0;1])); когда прямая находится между (1) и (2), то система будет иметь 3 решения; когда прямая находится в положении (2), то система будет иметь одно решение: (x=1, y=1).
Прямая (y=-x+a) находится в положении (1) при (a=1), в положении (2) – при (a=2), следовательно, [ain [1;2)]

Ответ:

([1;2))

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Источник