Marval
[2.1K]
6 лет назад
AM=1
AN^2=DN^2+AD^2: AD=2; DN^2=DC^2+CN^2=2^2+1^2=5
AN=sqrt(5+2^2)=sqrt(9)=3(sqrt-корень квадратный);
MN^2=MK^2+KN^2(точка К-середина DC):MK=2; KN^2=KC^2+CN^2=1+1=2
MN=sqrt(4+2)=sqrt(6);
точка Q-точка пересечения перпендикуляра с прямой MN;
AN^2=AQ^2+QN^2: AQ=y,Qm=x;QN=MN+QM=x+sqrt(6): 9=y^2+(x+sqrt(6))^2;
AM^2=AQ^2+QM^2: 1=x^2+y^2=>y^2=1-x^2;
9=1-x^2+(x+sqrt(6))^2=1-x^2+x^2+6+2sqrt(6)x=7+2sqrt(6)x
2=2sqrt(6)x=>x=1/sqrt(6)
y^2=1-1/6=5/6
y=sqrt(5/6)=sqrt(30)/6
автор вопроса выбрал этот ответ лучшим
комментировать
в избранное
ссылка
отблагодарить
It depends on the definition of «unit cube», but let’s go with what you proposed in the comments, i.e., the cube bounded by the planes $x=pmfrac12, y=pmfrac12, z=pmfrac12$.
A point lies on the surface of this cube if and only if the absolute value of its largest coördinate is $frac12$. Therefore the line segment in question is from $(frac12,frac14,-frac12)$ to $(-frac12,-frac14,frac12)$. The point $(1,frac12,-1)$, in contrast, is on the line, but outside the cube because it is on the wrong side of the planes $x=frac12$ and $z=-frac12$.
It can be helpful for problems like this to solve a similar problem in a lower dimension: try finding the length of the line segment in the unit square along the line $frac x2=y$, for example. You can draw a diagram much more easily this way and see how it relates to the equations.
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
10 класс. Геометрия. Параллельные прямые в пространстве.
10 класс. Геометрия. Параллельные прямые в пространстве.
- Оглавление
- Занятия
- Обсуждение
- О курсе
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
1. Тема и цели урока
Мы уже изучали параллельные прямые в планиметрии. Теперь нужно дать определение параллельных прямых в пространстве и доказать соответствующие теоремы.
2. Определение параллельных прямых в пространстве
Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).
Обозначение параллельных прямых: a || b.
3. Теорема 1 и ее доказательство
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Дано: прямая а, (Рис. 2.)
Доказать: существует единственная прямая b || a,
Через прямую а и точку , не лежащую на ней, можно провести единственную плоскость α (Рис. 3.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.
Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 2). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.
4. Лемма (о двух параллельных прямых, пересекающих плоскость) и ее доказательство
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Дано: а || b,
Доказать:
Доказательство: (Рис. 4.)
Существует некоторая плоскость β, в которой лежат параллельные прямые а и b. Точка М принадлежит и плоскости α, и прямой а, которая лежит в плоскости β. Значит, М – общая точка плоскостей α и β. А по третьей аксиоме, существует прямая MN, по которой пересекаются эти две плоскости.
Прямая MN пересекается с прямой b.(так как в противном случае, получается, что прямые MN и b параллельные, то есть a = MN, что невозможно, так как прямая а пересекается с плоскостью α в точке М по условию). То есть точка N – это точка пересечения прямой b и плоскости α..
Докажем, что N — это единственная общая точка прямой b и плоскости α. Допустим, что есть другая точка, но тогда прямая bпринадлежит плоскости α (по второй аксиоме). То есть MN = b, что невозможно, так как прямые а и bпараллельны, а прямая а должна пересекаться с прямой MN. Лемма доказана.
5. Теорема 2 и ее доказательство
Если две прямые параллельны третьей, то они параллельны.
Дано:
Доказать: .
Доказательство: (Рис. 5.)
Выберем произвольную точку К на прямой b. Тогда существует единственная плоскость α, проходящая черезточку К и прямую а. Докажем, что прямая bлежит в плоскости α.
Предположим противное. Пусть прямая bне лежит в плоскости α. Тогда прямая bпересекает плоскость α в точке К. Так как прямые bи с параллельны, то, согласно лемме, прямая с также пересекает плоскость α. Прямые а и с также параллельны, значит, по лемме, прямая а также пересекает плоскость α, но это невозможно, так как прямая а лежит в плоскости α. Получили противоречие. То есть, предположение было неверным, а значит, прямая bлежит в плоскости α.
Докажем, что прямые а и b не пересекаются. Предположим противное. Пусть прямые а и bпересекаются в некоторой точке М. Но тогда получается, что через точку М проходят две прямые а и b, параллельные прямой с, что невозможно в силу теоремы 1. Получили противоречие. Значит, прямые а и b не пересекаются.
Мы доказали, что прямые а и b не пересекаются и что существует плоскость α, в которой лежат прямые а и b. Значит, прямые а и bпараллельны (по определению), что и требовалось доказать.
6. Итоги урока
Итак, мы дали определение параллельных прямых и доказали теорему о параллельных прямых в пространстве. Также мы доказали важную лемму о пересечении параллельными прямыми плоскости и с помощью этой леммы доказали теорему: если две прямые параллельны третьей, то они параллельны. Эта теория будет использоваться дальше и для доказательства других теорем, и для решения задач.
Перечислить и указать в кубе прямые параллельные плоскости BDC1?
Геометрия | 10 — 11 классы
Перечислить и указать в кубе прямые параллельные плоскости BDC1.
Прямая, нележащая в плоскости, параллельна этой плоскости, если данная прямая параллельна хотя бы одной прямой лежащей в данной плоскости
из рисунка видно, что прямая BC1 лежит в плоскостиBDC1, а прямая АD1 параллельна ВС1 (АD1 || BC1) — так как лежат в параллельных гранях и являются равными диагоналями этих граней, значитАD1 параллельна плоскостиBDC1, то естьАD1||(BDC1)
аналогично АВ1 || C1D = > ; AB1 ||(BDC1)
B1D1 || BD = > ; B1D1 ||(BDC1)
отв : B1D1 ; АВ1 иАD1.
Две прямые одной плоскости соответственно параллельны двум прямым другой плоскости?
Две прямые одной плоскости соответственно параллельны двум прямым другой плоскости.
Можно ли утверждать что плоскости параллельны.
Верно ли утверждение, прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости?
Верно ли утверждение, прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости?
Прямая n параллельна прямой m параллельна плоскости а?
Прямая n параллельна прямой m параллельна плоскости а.
Следует ли из этого, что прямая n параллельна плоскости а.
Выберите верные утверждения?
Выберите верные утверждения.
А) Прямая, не лежащая в данной плоскости и параллельная какой либо прямой на плоскости, параллельна самой плоскости.
Б) Плоскость, проходящая через одну из двух параллельных прямых, параллельна другой прямой.
В) Через точку, не принадлежащую плоскости, можно провести бесконечное число прямых, параллельных данной плоскости.
Г) Через одну из двух параллельных прямых можно провести плоскость, параллельную другой прямой, и только одну.
Д) Если две прямые параллельны одной плоскости, то они параллельны друг другу.
Плоскости параллельны?
Прямая а лежит на плоскости.
Верно ли, что прямая а параллельна любой прямой, лежащей в плоскости.
Отметьте верные утверждения?
Отметьте верные утверждения.
1. Прямая параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости.
2. Через одну из двух параллельных прямых можно провести бесконечное множество плоскостей, параллельных другой прямой.
3. Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой плоскости, то эти плоскости параллельны.
4. Если две плоскости параллельны одной и той же прямой, то они параллельны.
Одна из двух параллельных плоскостей перпендикулярна прямой, тогда : а)другая плоскость параллельна прямой ; б) прямая лежит в другой плоскости ; в)другая плоскость перпендикулярна прямой ; г)перямая ?
Одна из двух параллельных плоскостей перпендикулярна прямой, тогда : а)другая плоскость параллельна прямой ; б) прямая лежит в другой плоскости ; в)другая плоскость перпендикулярна прямой ; г)перямая не пресекает другую плоскость ; д) выполняются все случаи, указанные в пунктах а — г.
Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой?
Докажите, что если плоскость проходит через прямую, параллельную другой прямой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна первой прямой.
Две плоскости пересекаются по прямой а ?
Две плоскости пересекаются по прямой а .
Прямая b лежит в одной из плоскостей и не параллельна другой плоскости .
Параллельные ли прямые а и b.
Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельн?
Выберете верное утверждение : а)если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая лежит в данной плоскости ; б)если плоскость альфа проходит через прямую, параллельную плоскости бета, то и плоскость альфа параллельна плоскости бета ; в)если две прямые пересекают плоскость, то они параллельны ; г)прямая и плоскость называется параллельными, если они не имеют общих точек.
Перед вами страница с вопросом Перечислить и указать в кубе прямые параллельные плоскости BDC1?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
Площадь боковой поверхности S = (АВ + ВС + СD + АD)·АМ = 26·АМ. По условию 26·АМ = 260. АМ = 260 / 26 = 10 см. Ответ : 10 см.
Площадь параллелограмма : S = a * b * sinα, α — угол между сторонами параллелограмма а = 3 см b = 12 см S = 18 см² 18 = 3 * 12 * sinα, sinα = 1 / 2. Α = 30° β = 180° — 30°, β = 150° (α + β = 180°. Сумма углов параллелограмма прилежащих к одной стор..
Если PL = 72°, KM = 72 * Они вертикальны. 180 — 72 = 108.
Ответ д, там получается две параллельные прямые пересечены секущей, треугольник ABN получается равнобедренный, AN = AB a AB = корень (25 — 9) = 4.
АВ = 12 см — СЕ = 4 см АВ = 8 см — СЕ = 2 см АВ = 10 см — СЕ = 2 см.
Решение — в приложении.
Остроугольный треугольник, потому что каждый угол меньше 90 градусов.
45 градусов. Так как МС биссектриса а она делит угол С пополам.
Так как мс биссектриса, то угол mca равен 1 / 2 bca ответ : 45 градусов.
http://www.kursoteka.ru/course/2156/lesson/6859/unit/17941/3
http://geometria.my-dict.ru/q/4790343_perecislit-i-ukazat-v-kube-pramye/
План урока:
Понятие перпендикуляра
Расстояния между плоскостями и прямыми
Теорема о трех перпендикулярах
Угол между прямой и плоскостью
Задачи на перпендикуляры, наклонные, расстояния
Понятие перпендикуляра
Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.
Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:
Запомним некоторые геометрические термины. В таком построении:
- отрезок МН – это наклонная;
- отрезок НК – это проекция наклонной, или просто проекция;
- К – основание перпендикуляра;
- Н – основание наклонной.
Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).
Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.
Расстояния между плоскостями и прямыми
Докажем довольно очевидный факт:
Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:
Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.
Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.
Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.
Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.
Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:
Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.
Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.
Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.
Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.
Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:
Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:
Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.
Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.
Далее через K в плоскости γ проведем прямую р’, параллельную р:
Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:
В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.
Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.
Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).
Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.
Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.
Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.
Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.
Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:
Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.
Итак, из всех наших рассуждений мы можем сделать следующие выводы:
Теорема о трех перпендикулярах
Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.
Проиллюстрируем теорему с помощью картинки:
Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.
Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):
Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.
Угол между прямой и плоскостью
Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.
Пусть надо определить угол между прямой HM и плоскостью α:
Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.
Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:
Задачи на перпендикуляры, наклонные, расстояния
Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.
Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:
Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.
Ответ: 1.
Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.
Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:
Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:
Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.
Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.
Найти АК можно с помощью тригонометрии в ∆АКD:
Задание. Найдите расстояние от H до плоскости EDG:
Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:
Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.
В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.
Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.
Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.
Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.
Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:
Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:
Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:
Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:
Задание. Найдите расстояние между прямыми ВС и DH:
Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.
Ответ: 1.
Задание. Каково расстояние между прямыми ВС и DG:
Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:
Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.
Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:
Задание. Найдите расстояние между ребрами АВ и HG:
Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.
Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:
Задание. Чему равно расстояние между ребром AB и диагональю FD:
Решение. Пусть А1, D1, H1 и Е1 – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А1, D1, H1 плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:
Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.
Заметим, что в четырехугольнике АА1D1D стороны АА1 и DD1 параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА1D1D – параллелограмм. Более того, раз у него есть прямые углы ∠А1АDи ∠АDD1, то можно утверждать, что АА1D1D – прямоугольник. Тогда АD||A1D1. Аналогично можно показать, что DHH1D1 – прямоугольник, и DH||D1H1.
Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А1D1и D1H1, а в плоскости ADH находятся прямые AD и DH, и АD||A1D1, и DH||D1H1, то по этому признаку α||ADH.
Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD1. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A1D1и D1H1 в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.
Отсюда вытекает, что α должна проходить через середину Е1. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА1, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е1.
Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е1D1. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:
Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е1FD = ∠D1DF (накрест лежащие углы при секущей FD). ∠FKE1 и ∠DKD1 одинаковы уже как вертикальные углы. Тогда ∆FKE1 и ∆DKD1 подобны по 2 углам. Но отрезки FE1 и DD1 одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE1 и ∆DKD1 равны, и поэтому Е1К = KD1. Это и значит, что К – середина Е1D1.
Также отметим, что Е1D1 – диагональ в четырехугольнике А1Е1Н1D1. Докажем, что А1Е1Н1D – это квадрат. Ранее мы уже показали, что АА1D1D и DHH1D1 – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА1Е1Е и ЕЕ1Н1Н. Из этого вытекает равенство сторон:
То есть в А1Е1Н1D1 все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А1D1H1. AD⊥CDHG и AD||A1D1, поэтому А1D1⊥CDHG. Значит, также А1D перпендикулярна любой прямой на грани CDHG, в том числе и D1H1. То есть ∠А1D1H1 = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.
Итак, мы выяснили, что А1Е1Н1D1 – квадрат, а К – середина его диагонали Е1D1. Получается, что К – точка пересечения диагоналей квадрата А1Е1Н1D1, ведь эта точка пересечения как раз делит диагонали пополам.
Теперь мы можем наконец доказать, что А1К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А1К принадлежит α, то А1К⊥АВ. Но как же доказать, что А1К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е1К – это проекция FK на α, и Е1К⊥А1К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А1К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А1К⊥FK.
Осталось лишь вычислить длину А1К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А1Е1К, в котором ∠А1Е1К = 45°:
Отвлечемся от куба и рассмотрим другую задачу.
Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?
Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть
Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:
Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.
Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.
Задание. Найдите угол между ребром куба BD и гранью СDHG:
Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:
Ответ: 45°.
Задание. Вычислите угол между ребром CD и плоскостью BDHF:
Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:
Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.
Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.
Ответ: 45°
Задание. Чему равен угол между прямой BD и плоскостью ABGH:
Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:
Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.
В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.
ВD найдем из прямоугольного ∆ABD:
Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:
По таблице синусов легко определить, что ∠DBK = 30°.
Ответ: 30°.
В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.
0
Как решить задачу об отрезке в кубе?
Дан куб ABC…D1 с ребром 2.
Точка М — середина АВ. N — середина СС1.
Как найти расстояние от А до прямой MN?
1 ответ:
1
0
AM=1
AN^2=DN^2+AD^2: AD=2; DN^2=DC^2+CN^2=2^2+1^2=5
AN=sqrt(5+2^2)=sqrt(9)=3(sqrt-корень квадратный);
MN^2=MK^2+KN^2(точка К-середина DC):MK=2; KN^2=KC^2+CN^2=1+1=2
MN=sqrt(4+2)=sqrt(6);
точка Q-точка пересечения перпендикуляра с прямой MN;
AN^2=AQ^2+QN^2: AQ=y,Qm=x;QN=MN+QM=x+sqrt(6): 9=y^2+(x+sqrt(6))^2;
AM^2=AQ^2+QM^2: 1=x^2+y^2=>y^2=1-x^2;
9=1-x^2+(x+sqrt(6))^2=1-x^2+x^2+6+2sqrt(6)x=7+2sqrt(6)x
2=2sqrt(6)x=>x=1/sqrt(6)
y^2=1-1/6=5/6
y=sqrt(5/6)=sqrt(30)/6
Читайте также
Для простоты обозначим АЕ — х, а ВЕ — у. По т. Пифагора у² = 100 – х² и FE² = 42,25 — x².
Вместе с тем, треугольники BFC и EFA подобны, а значит, ВС/AE = BF/FE.
Учитывая, что BF= y – FE = y — √(42,25-x²), получим
13,2/х = (y — √(42,25-x²))/√(42,25-x²) = y/√(42,25-x²) – 1.
Таким образом, имеем систему уравнений:
{ у² = 100 – х²;
{13,2/х = y/√(42,25-x²) – 1.
В результате преобразований получим немного жутковатое кубическое уравнение:
26,4х³ + 231,99х² — 1115,4х – 7361,64 = 0,
единственным положительным корнем которого является х = 6 (честно сознаюсь, что уравнение решала не сама).
Теперь, когда известна длина AE, найти высоту параллелограмма не составит труда:
ВЕ = √(100-36) = 8.
Параметров свободных очень много. Можно выбирать любые. Выберем банальное перпендикулярное пересечение.
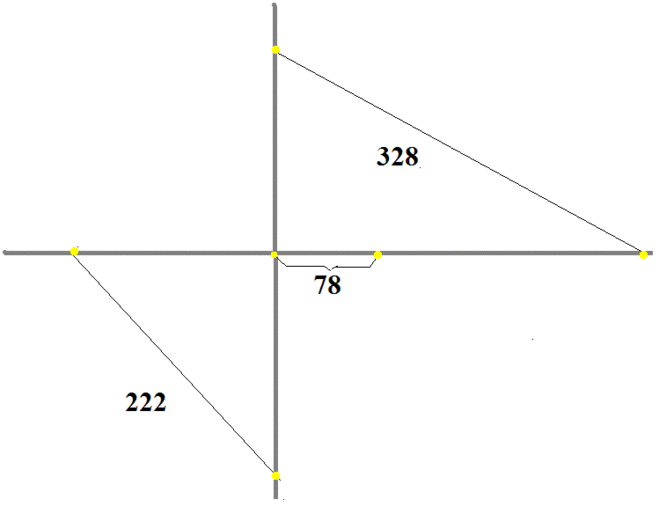
Один автомобиль едет по оси Ох со скоростью V км/мин , другой по Оy со скоростью U км/мин. А через 145 минут после начала движения автомобиль с меняющейся игрековой координатой оказывается ровно на перекрестке. Координаты в начальный момент соответственно x и y.
x^2 + y^2 = 328^2
x — 145V = 78
y = 145U
(120V-78)^2+(120U)^2<wbr />=222^2
Второе и третье подставляем в первое
(78+145V)^2 + (145U)^2 = 328^2
отсюда выражаем U через V
U^2 =(328^2 — (78+145V)^2) / 145^2
подставляем в четвёртое
(120V — 78)^2 +(120/145)^2 * (328^2 — (78+145V)^2) = 222^2
V =46,153845 км/час = 0,76923075 км/мин (приблизительно)
Соответственно U =1,84615386 км/мин = 110,7692315862 км/час
x=189,53845875 км
y=267,69230967 км
<hr />
Осталась мелочь: догадаться, что нужно поменять, чтобы автомобили достигли перекрёстка одновременно?
Проще всего поменять скорость самих автомобилей и время, через которое состоится встреча, оставив неизменным угол между дорогами и начальные координаты автомобилей.
Попросим автомобили встретиться через час.
За этот час они сблизятся на 328 км. Надо полагать, что скорость сближения 328 км/час
А если попросим встретиться через два часа?
Тогда скорость сближения будет ровно в два раза меньше.
<hr />
Можно оставить в покое скорости автомобилей, но дать им другие точки старта,
время встречи возьмём из условия через 2 ч 25 мин
Для автомобиля, который и так через это время будет на перекрёстке, ничего менять не будем.
Ну, а второй передвинем влево на 78 км. x = 111,53845875 км
Расстояние между автомобилями s = sqrt(x^2+y^2)=290 км
скорость сближения 290/145 = 2 км/мин = 120 км/час
Но нарушено условие про начальное расстояние между автомобилями.
<hr />
Сохраним начальное расстояние между автомобилями, но не будем обращать внимания на промежуточное время.
(Ut)^2 + (Vt)^2 = 328^2 => t = 328/sqrt(U^2 + V^2) =164 минуты.
скорость сближения 290/145 = 2 км/мин = 120 км/час
Общее время автопробега 265 мин, после встречи 101 мин. Конечное расстояние
(101/60) * sqrt( U^2 + V^2 )=222 км
С некоторой попытки угадалось, какое число из условия можно выбросить, а какие нельзя.
Какому-то древнему греку взбрело в голову померять землю, а так как землю древние греки обзывали «гео», то измерение земли назвали геометрией. Сначала меряли плоские структуры, выводили законы и зависимости геометрии, потом распространили в третье измерение. Евклид собрал все эти достижения в своей книге «Начала», котрая стала учебником «евклидовой геометрии». В 17 веке Декарт придумал координаты и заложил основы аналитической геометрии. Уже не надо было чертить, стало можно считать пользуясь отношением координат точек примитивов.
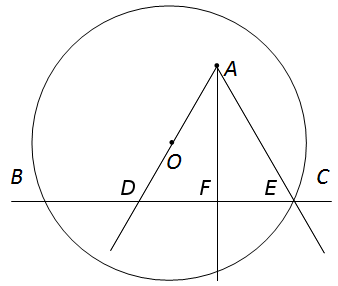
Если линейка градуированная, то окружность не нужна для ответа на вопрос.
- Кладём линейку под любым острым углом к прямой ВС и проводим по линейке прямую, проходящую через точку А и пересекающую прямую ВС.
- Измеряем длину отрезка AD.
- Поворачиваем линейку так, чтобы её нулевое деление совпадало с точкой А. Останавливаем вращение, когда деление линейки, соответствующее длине AD, окажется на прямой BC. Проводим прямую по линейке и получаем точку Е пересечения этой прямой с прямой ВС.
- Измеряем длину отрезка DE и полученную величину делим на 2.
- Отрезок такой половинной длины откладываем на прямой ВС от точки D (отрезок DF) либо от точки Е (отрезок EF).
- Проводим прямую, проходящую через точки А и F, она и будет перпендикулярна прямой ВС.
Можно попробовать пересчитать. Хотя бы приблизительно.
Плоские фигуры: треугольник (и его разновидности: равносторонний, равнобедренный, прямоугольный), квадрат, прямоугольник, ромб, параллелограмм, трапеция, круг (и его части — сектор и сегмент), овал, эллипс. Немногим больше десятка набралось. Можно еще добавить звезду (звезд разных тоже много).
Объемные фигуры: куб, призма (они бывают тоже разные, например, прямая, треугольная и т.д.), конус (а бывает еще усеченный конус), цилиндр (прямой, наклонный), пирамида (тоже несколько разновидностей), тор, шар (а также шаровой слой и шаровой сектор, и можно добавить эллипсоид и геоид), параллелепипед, тетраэдр, октаэдр, додекаэдр, икосаэдр (а есть еще усеченный икосаэдр — такую форму имеет бакминстерфуллерен из 20 шестиугольников и 12 пятиугольников). Всего разных названий — около 30. Возможно, какие-то пропущены. Но индивидуальных названий геометрических фигур и тел не так уж много.