Как найти длину отрезка в трапеции решение - Исправление недочетов и поиск решений вместе с Examum.ru

Трапеция. Формулы, признаки и свойства трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
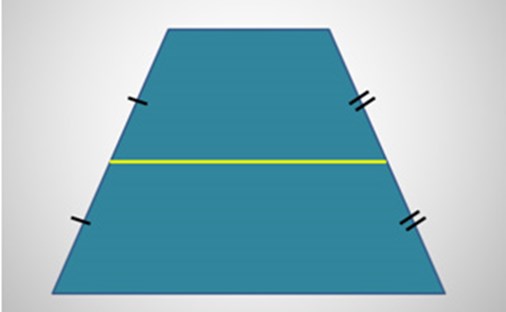
Средняя линия — отрезок, соединяющий середины боковых сторон.

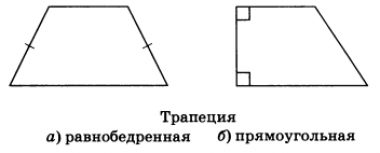
Виды трапеций:

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

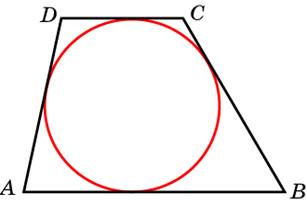
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
2m	2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab —	a(d ² — c²)
a — b

d₂ =	√	c² + ab —	a(c² — d ²)
a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

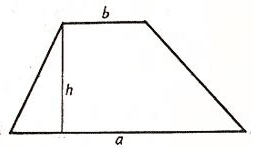
1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c² —	(	(a — b)² + c² — d ²	)	²
2	2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
\|a — b\|

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
4√p(p — a)(p — c)(p — d₁)

где

a — большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Источник

геометрия — Нахождение длины отрезка в трапеции

В трапеции ABCD с основаниями AD и BC имеем AB=3, BC=1. Точка P лежит на стороне AB, а точка Q — на стороне CD, причем отрезок PQ параллелен основаниями и проходит через точку пересечения диагоналей трапеции. Найти длину отрезка PQ.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

Связанные исследования

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Источник

Ну про гугл это не ко мне. Но задачу вам решу.

Обозначим трапецию ABCD, (нижнее основание AD=a, верхнее BC=b) точку пересечения диагоналей — O, линию параллельную основаниям и проходящую через O обозначим — MN. Смотрим рисунок.

1) Рассмотрим ∆ВСО и ∆ADO — они подобны по 2 углам. ∠CBO=∠ADO (накрест лежащие при параллельных прямых) и углы O — вертикальные. Соответственно коэффициент подобия равен отношению сторон AD/BC = a/b

Проведем высоту EF через точку O, соответсвенно OF и OE — высоты в ∆ADO и ∆ВСО и тоже относятся с коэффициентом подобия : OF/OE = a/b

Ну а дальше идет решение такое же как при выводе формулы средней линии.

2) Проводим высоты BH₁ и CH₂. Смотрим ∆AH₁B и ∆MKB — они подобны по 2 углам: ∠B — общий и они прямоугольные. И AH₁/MK = KH₁/KB = OF/OE = (a+b)/b. Откуда MK = AH₁•b/(a+b)

Аналогично из подобия ∆CH₂D и ∆CLN: LN = DH₂•b/(a+b)

Так как KL = BC = b, то

MN = MK + KL + LN = b + (b/(a+b))•(AH₁ + DH₂)

Теперь посмотрим на AD: AD = AH₁ + H₁H₂ + DH₂, так как AD = a, H₁H₂ = BC = b, то

AH₁ + DH₂ = a — b

И получаем

MN = b + (b/(a+b))•(a-b) = b•(a+b) + b•(a-b)/(a+b) = b•2a/(a+b) = 2ab)/(a+b)

Ответ: MN = 2ab/(a+b)

Источник

Следующие задания с расширенным ответом из открытого банка ФИПИ к ОГЭ по математике, раздел геометрия, могут вам попасться на реальном экзамене в этом году. В статье приведены задачи типа, — пряма параллельная одному из оснований пересекает боковые стороны, найти номинал отрезка образованного между этими сторонами.

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

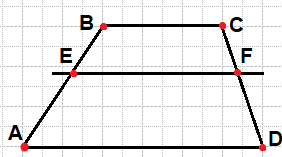
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.

55CB45

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.

DCE2BA

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.

89A535

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=33, BC=18, CF:DF=2:1.

5D0CC5

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=20, CF:DF=4:1.

D90C6D

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=36, BC=18, CF:DF=7:2.

B53A99

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=35, BC=21, CF:DF=5:2.

C2A1CF

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=48, BC=16, CF:DF=5:3.

3D72D5

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=27, CF:DF=5:4.

292E1E

Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=50, BC=30, CF:DF=7:3.

60A16B

Источник

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k².
Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т.
Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ.
А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b).

Свойства средней линии трапеции

Среднюю линию проведите в трапеции параллельно ее основаниям.

Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2.
Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.

Свойство биссектрисы трапеции

Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.

Свойства углов трапеции

Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180⁰: α + β = 180⁰ и γ + δ = 180⁰.
Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90⁰, длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2.
Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции

В равнобедренной трапеции равны углы при любом из оснований.
Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
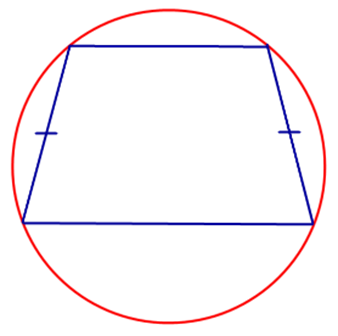
Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180⁰ – обязательное условие для этого.
Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2.
Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2.

Свойства трапеции, вписанной в окружность

Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.

Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ.
Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S_АМЕ.

Свойства трапеции, описанной около окружности

Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.

Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2.
У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ.
Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab.
И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.

Свойства прямоугольной трапеции

Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.

У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.

Доказательства некоторых свойств трапеции

Равенство углов при основании равнобедренной трапеции:

Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.

АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.

Откуда АКМ = 180⁰— МЕТ = 180⁰— КАЕ = КМЕ.

Что и требовалось доказать.

Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной:

Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).

∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.

МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.

У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.

Задача для повторения

Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150⁰ с меньшим основанием. Требуется найти площадь трапеции.

Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.

Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180⁰. Поэтому КАН = 30⁰ (на основании свойства углов трапеции).

Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30⁰. Поэтому КН = ½АВ = 4 см.

Площадь трапеции находим по формуле: S_АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см².

Послесловие

Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.

Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.

Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!

Источник

Трапеция. Формулы, признаки и свойства трапеции

Основные свойства трапеции

Сторона трапеции

Формулы определения длин сторон трапеции:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

Высота трапеции

Формулы определения длины высоты трапеции:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

Площадь трапеции

Формулы определения площади трапеции:

Периметр трапеции

Формула определения периметра трапеции:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

геометрия — Нахождение длины отрезка в трапеции

Здравствуйте

Связанные исследования

Связанные вопросы

Отслеживать вопрос

Задания из банка ФИПИ к ОГЭ по математике, геометрия части 2

Трапеция и все-все-все

Свойства диагоналей трапеции

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521509/_________5.jpg?width=506px&amp;height=312px" width="506" height="312" alt="Трапеция 2" />

Свойства средней линии трапеции

Свойство биссектрисы трапеции

Свойства углов трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521514/_________2.png" width="380" height="153" alt="Трапеция 2" />

Свойства равнобедренной (равнобокой) трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521519/_________4.png?width=338px&amp;height=336px" width="338" height="336" alt="Трапеция 4" />

Свойства трапеции, вписанной в окружность

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521524/_________6.jpg" width="307" height="205" alt="Трапеция 6" />

Свойства трапеции, описанной около окружности

Свойства прямоугольной трапеции

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://blog.tutoronline.ru/media/521529/_________3.gif" width="254" height="148" alt="Трапеция 3" />

Доказательства некоторых свойств трапеции

Задача для повторения

Послесловие