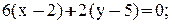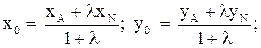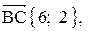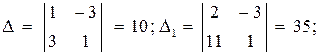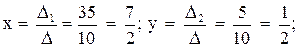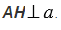Как найти длину перпендикуляра в координатах

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1)?

Математика | 10 — 11 классы

Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1).

(x + 2) / 8 = (y + 5) / 4

AD = I — 3 — 4 — 8I / (srqt(1 + 4)) = 15 / sqrt5 = 3 * srqt5

(x + 3) / 1 = (y — 2) / ( — 7)

y + 1 = ( — 1 / 7)(x — 6)

Найти длину перпендикуляра опущенного из начала координат на прямую : (х — 1) / 7 = (у — 1) / 9 = (z — 1) / 11?

Найти длину перпендикуляра опущенного из начала координат на прямую : (х — 1) / 7 = (у — 1) / 9 = (z — 1) / 11.

Катеты прямоугольного треугольника АВС равны 3см?

Катеты прямоугольного треугольника АВС равны 3см.

Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр СД = 1см.

Найти расстояние от точки Д до гипотенузы АВ.

Высота и биссектриса прямоугольного треугольника, опущенная из вершины прямого угла, равны, соответственно, 6 и 8?

Высота и биссектриса прямоугольного треугольника, опущенная из вершины прямого угла, равны, соответственно, 6 и 8.

Найдите площадь треугольника.

Доказать, что радиус описанной окружности, проведенный в одну из вершин треугольника, перпендикулярен прямой, соединяющей основания высот, проведенных из двух других вершин треугольника?

Доказать, что радиус описанной окружности, проведенный в одну из вершин треугольника, перпендикулярен прямой, соединяющей основания высот, проведенных из двух других вершин треугольника.

1. Вычислите : 125 в степени 2 / 3 — 0?

1. Вычислите : 125 в степени 2 / 3 — 0.

22. Катет прямоугольного треугольника соответственно равен 12 см.

. Площадь треугольника равна 30 см 2.

Найти длину высоты, опущенной из вершины прямого угла.

23. Основанием прямого конуса является круг с площадью, равной 9 .

Образующая конуса равна 5.

Найти объем конуса 25.

Катеты прямоугольного треугольника соответственно равны 12 см и 5 см.

Найти длину высоты, опущенной из вершины прямого угла11.

Радиус окружности, описанной около прямоугольного треугольника, равен 6 см.

Один катет равен 5 см.

Найти площадь треугольника.

Даны координаты вершины треугольника А(х1 ; у1), В(х2 ; у2), С(х3 ; у3)?

Даны координаты вершины треугольника А(х1 ; у1), В(х2 ; у2), С(х3 ; у3).

Найти : длину стороны АВ ; уравнения сторон треугольника ; внутренний угол при вершине А ; уравнение высоты проведенной через вершину С ; уравнение медианы проведенной через вершину В ; точку пересечения высот ; площадь треугольника АВС.

А( — 4 ; 2) В(0 ; — 1) С(3 ; 3).

ПОМОГИТЕЕ ПОЖАЛУЙСТАА В равнобедренном прямоугольном треугольнике с катетами , равными 4 корень из 2, найти высоту опущенную на вершины прямого угла?

ПОМОГИТЕЕ ПОЖАЛУЙСТАА В равнобедренном прямоугольном треугольнике с катетами , равными 4 корень из 2, найти высоту опущенную на вершины прямого угла?

Найти высоту, опущенную из вершины равнобедренного треугольника, если угол при вершине равен 2п / 3, а площадь треугольника равна 9корень3?

Найти высоту, опущенную из вершины равнобедренного треугольника, если угол при вершине равен 2п / 3, а площадь треугольника равна 9корень3.

Помогите пожалуйста ?

Точки A(1 ; 4), В( — 2 ; — 2) и С(4 ; 1) являются вершинами треугольника АВС.

Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС.

Определить координаты точки Н — основания высоты АН треугольника АВС.

Даны вершины А, В, и С треугольника?

Даны вершины А, В, и С треугольника.

Длину стороны АВ.

2. уравнение сторон АВ и АС.

4. Уравнение высоты СД, опущенной из вершины С и ее длину.

5. Уравнение медианы, проведенной через вершину С.

6. уравнение прямой, проходящей через вершину С параллельно стороне АВ.

Вы открыли страницу вопроса Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1)?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

14, 4 * 2 / 3 = 9, 6 км / ч(Скорость 2) 14, 4 + 9, 6 = 24 км / ч(Общая скорость) 42 / 60 = 0, 7 часа 24 * 0, 7 = 16, 8 км (Растояние между деревнями).

V1 = 14, 4км / ч v2 = ? , 2 / 3 t = 42 мин S = ? Решение : V2 = (14, 4 : 3) * 2 = 9, 6км / ч S = t * v S = (42 : 60)•(14, 4 + 9, 6) = 0, 7 + 24 = 24, 7м P. S. надеюсь что так))).

2300 / 4 = 575 575 — 350 = 225.

123456789 * 2007 = 247777775523 123456789 * 2007 = 247777775523 247777775523 — 247777775523 = 1.

400 800 4000 5тон 1 кг 4 тонни 1 кг 3 км 3 км 90 см — 0. 09метрів 100см — 0, 01метрів.

1)35 * 2 = 70(ч) плул катер 2)35 + 3 = 38(км / ч) увеличенная скорость 3)38 * 2 = 76(км) проплыл катер с увеличенной скоростью Ответ : 76 км.

1 2 2 1 10 — 2 + 5 = 13 25 — 25 : 5 = 20 1 2 2 1 18 : 3 • 2 = 12 10 + 3 • 2 = 16 1 1 2 1 25 — 5 • 2 = 15 10 + 10 : 2 = 15 3 1 2 2 1 3 25 — (2 + 3) : 5 = 24 4 • (2 + 3) + 2 = 22 3 2 1 12 + 1 • (3 — 1) = 14.

21 ц = 2100 кг 35 т = 35000 кг 208000 г = 208 кг 90000 г = 90 кг 6 ц = 600 кг 2 т 35 кг = 2035 кг.

(156, 8 — 28, 2) : 2 = 64, 3 64 ; 3 + 28, 2 = 92, 5 64, 3га и 92, 5 га.

1000 метр. Ghastly kink hi David bmp im Tuesday network budget.

Уравнение высоты треугольника по координатам формула

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Даны координаты вершин треугольника .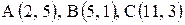

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

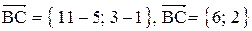
2. Уравнение прямой ВС: ; ; .

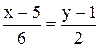
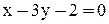
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

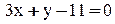
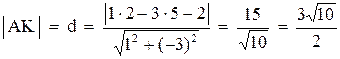
4. Найдем координаты точки N – середины стороны ВС:

; ; .

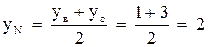
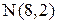
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

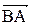
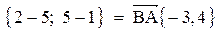
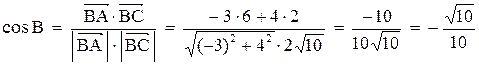
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

.

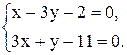
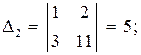
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	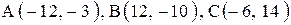.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	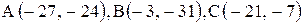.	10.	.
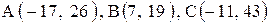11.	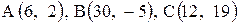.	12.	.
13.	.	14.	.
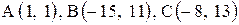15.	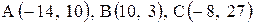.	16.	.
17.	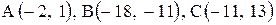.	18.	.
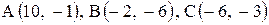19.	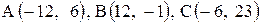.	20.	.
21.	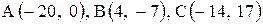.	22.	.
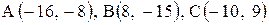23.	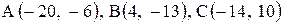.	24.	.
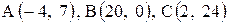25.	.	26.	.
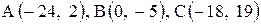27.	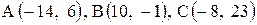.	28.	.
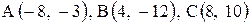29.	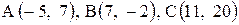.	30.	.

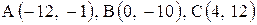Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10637 – | 8008 – или читать все.

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @

Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)

Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:

Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0

Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9

Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:

y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.

10 = (32/3) + d,
d = -2/3

Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0

Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: X_E = 6, Y_E = -1

Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.

(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0

Это уравнение медианы AE.

Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:

S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)

Как найти длину перпендикуляра

Даны точка и прямая представленная уравнением (1) § 161. Требуется найти расстояние от точки до прямой т. е. длину перпендикуляра (см. рис. 175), опущенного из точки на прямую .

Можно сначала найти основание К перпендикуляра (§ 161, пример), затем длину отрезка Проще применить формулу (при обозначениях § 161)

т. е. в векторной форме

Числитель выражения (1а) есть площадь параллелограмма (§ 111) , а знаменатель — длина основания Следовательно, дробь равна высоте параллелограмма.

Расстояние от точки до прямой

Что называется расстоянием от точки до прямой? Как найти расстояние от точки до прямой?

Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из данной точки на прямую.

Таким образом, чтобы найти расстояние от точки до прямой, надо из точки к прямой провести перпендикуляр и найти его длину.

Например, на рисунке 1 расстояние от точки A до прямой a равно длине перпендикуляра AB, опущенного из точки A на прямую a.

Задачи на нахождение расстояния от точки до прямой сводятся к рассмотрению прямоугольного треугольника.

№ 1. Из точки к прямой проведены две наклонные, длины которых относятся как 2:3, а длины их проекций соответственно равны 2 см и 7 см. Найти расстояние от точки до прямой.

Дано: A∉a,

BC и BD — их проекции, BC=2 см, BD=7 см

1) Пусть k — коэффициент пропорциональности. Тогда AC=2k см, AD=3k см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим k:

5) Зная k, найдем AB:

№ 2. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найти расстояние от точки до прямой, если разность проекций наклонных равна 4 см.

Дано: A∉a,

AC и AD — наклонные, AC=13 см, AD=15 см,

BC и BD — их проекции, BD-BC=4 см

1) Пусть BC=x см, тогда BD=x+4 см.

2) Рассмотрим треугольник ABC — прямоугольный (так как AB — перпендикуляр к прямой a по условию). По теореме Пифагора

3) Аналогично, из треугольника ABD

4) Приравниваем правые части полученных равенств и находим x:

5) Зная x, найдем AB:

№ 3. Найти расстояние от точки A до прямой a, если известно, что наклонная AF, длина которой равна c, образует с прямой a угол α.

Дано: A∉a,

Треугольник ABF — прямоугольный (так как AB — перпендикуляр к прямой a по условию). AB — катет, противолежащий углу ACB, AF — гипотенуза.

Основные сведения о перпендикуляре к прямой — что это такое, как находить

Каким будет определение положения прямой и плоскости, зависит от наличия общих точек. Если их больше одной, то прямая лежит на данной плоскости, если одна — то она ее пересекает. Если прямая не имеет с плоскостью точек пересечения, то прямая и плоскость параллельны.

Пересечение прямой линии и плоскости может происходить под разными углами. Если при пересечении между прямой и плоскостью образуется прямой угол, то такая прямая является к плоскости перпендикуляром. При этом она перпендикулярна всем прямым линиям, принадлежащим данной плоскости. Из этого свойства вытекает следующее определение.

Перпендикулярной к плоскости называется прямая линия, которая перпендикулярна всем без исключения прямым, лежащим в выбранной плоскости.

Следствием из данного определения является свойство плоскости, для которой установлено наличие перпендикуляра. Оно формулируется следующим образом: «Если плоскость перпендикулярна некоторой прямой, то она является также перпендикулярной для всех прямых, параллельных данной прямой».

В решении задач на построение перпендикуляров к плоскости в конкретной точке существует только одно решение, поскольку через определенную точку можно провести только одну прямую, занимающую по отношению к плоскости перпендикулярное положение.

О единственности такой прямой в геометрии существует доказательство.

Проведение перпендикуляра из точки к прямой

В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.

Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.

Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.

Такой отрезок будет кратчайшим соединением точки с прямой линией (и выбранной плоскостью).

Взаимное положение такого перпендикуляра и прямой обозначается специальным знаком.

Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.

Как построить перпендикуляр к прямой

Построить перпендикуляр к прямой можно несколькими способами:

1. С помощью циркуля.

Из выбранной точки P проводим полуокружность, которая пересекается с прямой в точках A и B.

Затем тем же радиусом строим две окружности, центры которых совпадают с точками A и B. При этом окружности проходят через точку P.

Следующим шагом будет соединение точек P и Q.

На данном рисунке перпендикуляр к прямой AB — отрезок PQ.

2. Вторым способом построения перпендикуляра является использование транспортира. Чтобы провести перпендикуляр, внимательно откладываем 90° от выбранной точки на прямой, используя при этом линейку транспортира. Отрезок, соединяющий эту точку и деление 90°, является перпендикуляром к прямой в заданной точке.

3. Третий способ был описан выше. Он основан на применении чертежного треугольника и линейки. С помощью линейки проводим прямую. Прикладываем к ней прямым углом треугольник и очерчиваем этот угол с двух сторон. Один отрезок совпадает с имеющейся прямой, а второй является перпендикуляром к ней.

Пояснение на примерах

В конспектах по геометрии присутствует понятие высоты, представляющей собой перпендикуляр к одной из сторон геометрической фигуры (например, треугольника).

Высотой треугольника называется перпендикуляр, который выходит из вершины треугольника и следует к противоположной стороне (либо к продолжению этой стороны, если треугольник тупоугольный).

В данном определении содержится отличие от основной характеристики биссектрисы, которая, опускаясь на противолежащую углу сторону, не является перпендикуляром к ней.

Аналогичная ситуация с определением медианы — линии, исходящей из угла треугольника и делящей противоположную сторону на две равные части.

Высоту треугольника можно провести из любого его угла, поэтому у каждого треугольника имеется три высоты.

Существует теорема, что все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

Используя свойство высоты треугольника о пересечении одной из его сторон под прямым углом, можно через высоту выразить формулу площади треугольника:

Уравнение для расчета высоты через площадь:

Найти через длины сторон:

h a = 2 p p — a p — b p — c a

где p — это полупериметр треугольника, который рассчитывается так:

p = a + b + c 2
Можно дать краткую характеристику еще двум способам выразить высоту треугольника:

Министерство
образования и науки Российской Федерации

Калужский
филиал федерального государственного
бюджетного образовательного учреждения
высшего профессионального образования

«Московский
государственный технический университет

имени
Н.Э. Баумана»

кафедра

Высшая
математика

Учебное пособие по курсу аналитической геометрии «Решение типовых задач»

Составил:
Влайков Н.Д.

Рецензент:
к.ф.-м.н. Савотин А.И.

г.
Калуга, 2011 г.

Содержание.

1. Уравнение
   прямой и плоскости в пространстве
   стр. 2

2. Уравнения
   кривых второго порядка
   стр.7

3. Матричные
   уравнения
   стр. 8

4. Решение
   СЛАУ
   стр. 10

5. Задачи
   для самостоятельного решения
   стр. 14

6. Список
   рекомендуемой литературы
   стр. 16

1. Уравнение плоскости и прямой в пространстве.

Даны
координаты четырех точек в пространстве
.

Найти:

1. Уравнение
   плоскости, проходящей через точки
   .

2. Уравнение
   и длину перпендикуляра, опущенного из
   т.
   на
   плоскость, проходящую через точки
   .

3. Расстояние
   от т.
   
   до прямой, проходящей через точки
   .

4. Точку,
   симметричную точке
   ,
   относительно прямой, проходящей через
   точки
   .

5. Выполнить
   чертеж.

Решение.

1.1.
Уравнение плоскости, проходящей через
три заданные точки,

,

имеет
вид:

.
Для наших точек:
.
Вычислим определитель:
следовательно,
уравнение искомой плоскости
.

1.2.
Составим уравнение перпендикуляра,
опущенного из т.
на
плоскость, проходящую через точки
.
Запишем это уравнение в каноническом
виде:
,
где
—
координаты точки, принадлежащей прямой,
а в знаменателях записаны соответствующие
координаты направляющего вектора
.
Координаты точки,
принадлежащей прямой, нам известны. В
качестве направляющего вектора, возьмем
нормальный вектор плоскости. Т.е.
_.

Запишем
уравнение перпендикуляра:
.

Длина
перпендикуляра может быть найдена как
расстояние от т.
до плоскости

по формуле:
,
где
,,—
координаты нормального вектора плоскости,
а

— координаты точки
.

.

1.3. Расстояние от т. До прямой, проходящей через точки .

а)
Общий вид уравнения прямой проходящей
через две заданные точки
,имеет
вид:
.
Для наших точек:

;
;

б)
Теперь найдем расстояние от точки
до
прямой
.
Для этого составим уравнение плоскости

,
проходящей через т.
,
перпендикулярно прямой
.
Уравнение плоскости, проходящей через
т.
,
с нормальным вектором

имеет вид:
.

Координаты
т.
известны,
а в качестве нормального вектора можно
выбрать направляющий вектор прямой
:

.
Подставим координаты в уравнение:
;
раскрыв скобки и приведя подобные
слагаемые получим уравнение плоскости

.

в)
Найдем координаты точки
—
точки пересечения прямой
и
плоскости
.
Точка
—
будет являться основанием перпендикуляра
опущенного из т.

на прямую
.
Т.к. т.

принадлежит и прямой и плоскости, ее
координаты должны удовлетворять двум
уравнениям, следовательно, координаты
можно найти, решив систему:

_;

Для
этого перейдем к параметрическому
уравнению прямой
:

;
выразим

через
параметр
:.

Подставим
в уравнение плоскости

и решим его:
;

.
Найдем

из системы:
;;.

Следовательно,
координаты т.
.

г)
Расстояние от т.

до прямой, проходящей через точки

можно найти как расстояние между точками

и

по формуле:
.

.

1.4.
Найдем координаты т.
,
симметричной точке
,
относительно прямой, проходящей через
точки
.
Координаты точки

можно найти из условия: т.
—
середина отрезка

(т.к. прямая
).
Координаты середины отрезка можно найти
по формулам:
,

,

.
Следовательно, координаты т.

можно
найти так:
,

,

.

Т.е.

,

,

.

.

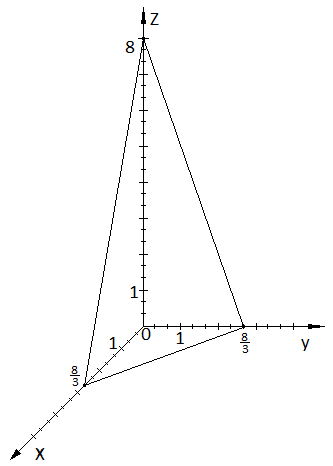
1.5.
Построим несколько поясняющих чертежей:

1.5.1.
Построим
точки
.
Для примера построим т.

Рис
1.1 Точка

1.5.2.
На рис 1.2 построим плоскость
,
приведя общее уравнение к уравнению
плоскости в отрезках:
;

;

Рис
1.2 плоскость
.

1.5.3.
Изобразим прямую
:

Рис
1.3 прямая

1.5.4.
Построим точку
:

Рис
1.4 Точка
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #