Примечание. Текст задачи взят с форума.
Задача.
| Катеты прямоугольного треугольника АВС равны 9 и 12 см. Через середину гипотенузы (точку О) провели перпендикуляр к плоскости треугольника, равный 6см. Найти расстояние от концов перпендикуляра до катетов. | Катети прямокутного трикутника АВС дорівнюють 9 і 12 см Через середину гіпотенузи (точку О) провели перпендикуляр до площини трикутника, рівний 6см. Знайти відстань від кінців перпендикуляра до катетів. |
Решение.
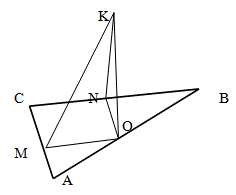
Отобразим условие задачи на рисунке
Обратим внимание на то, что ON и OM являются перпендикулярами к катетам прямоугольного треугольника, поскольку нам необходимо найти расстояние KN и KM.
Рассмотрим отрезок NO. Он является перпендикуляром к CB. Угол ACB также вляется прямым по условию задачи. Таким образом, треугольники ABC и OBN — подобны по признаку равенства углов (см. подобие треугольников). Угол В — общий, а, поскольку CA и NO являются перпендикулярами к CB — то остальные углы также равны (один прямой, второй равен 180 градусов минус сумма остальных углов, равенство которых мы уже доказали).
Коэффициент подобия треугольников равен соотношению BO к BA. Поскольку точка О — точка касания медианы прямоугольного треугольника к гипотенузе, то есть AO = OB, то коэффициент подобия будет равен 1:2.
Откуда ON = CA / 2 = 9 / 2 = 4,5
Расстояние же KN найдем по теореме Пифагора.
KN = √(4,5 2 + 6 2 ) = 7,5 см
Аналогично, найдем расстояние до второго катета:
Высота в прямоугольном треугольнике
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:
Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в раз:
При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , — высота, , . Найдите .
Рассмотрим треугольник . В нем известны косинус угла и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :
(поскольку значение синуса острого угла положительно). Тогда:
Рассмотрим прямоугольный треугольник , . Поскольку
2. В треугольнике угол равен , , . Найдите высоту .
Сделайте чертеж и рассмотрите прямоугольный треугольник .
3. В треугольнике угол равен , , . К гипотенузе проведена высота . Найдите .
Это чуть более сложная задача. Ведь вам неизвестны катеты и .
Зато можно записать теорему Пифагора: .
Нам известно также, что:
Решая эту систему из двух уравнений, найдем:
Запишем площадь треугольника АВС двумя способами:
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.
http://profmeter.com.ua/communication/learning/course/course7/lesson433/
http://ege-study.ru/ru/ege/materialy/matematika/vysota-v-pryamougolnom-treugolnike-i-ee-svojstva/
Примечание. Текст задачи взят с форума.
Задача.
| Катеты прямоугольного треугольника АВС равны 9 и 12 см. Через середину гипотенузы (точку О) провели перпендикуляр к плоскости треугольника, равный 6см. Найти расстояние от концов перпендикуляра до катетов. | Катети прямокутного трикутника АВС дорівнюють 9 і 12 см Через середину гіпотенузи (точку О) провели перпендикуляр до площини трикутника, рівний 6см. Знайти відстань від кінців перпендикуляра до катетів. |
Решение.
Отобразим условие задачи на рисунке
Обратим внимание на то, что ON и OM являются перпендикулярами к катетам прямоугольного треугольника, поскольку нам необходимо найти расстояние KN и KM.
Рассмотрим отрезок NO. Он является перпендикуляром к CB. Угол ACB также вляется прямым по условию задачи. Таким образом, треугольники ABC и OBN — подобны по признаку равенства углов (см. подобие треугольников). Угол В — общий, а, поскольку CA и NO являются перпендикулярами к CB — то остальные углы также равны (один прямой, второй равен 180 градусов минус сумма остальных углов, равенство которых мы уже доказали).
Коэффициент подобия треугольников равен соотношению BO к BA. Поскольку точка О — точка касания медианы прямоугольного треугольника к гипотенузе, то есть AO = OB, то коэффициент подобия будет равен 1:2.
Откуда ON = CA / 2 = 9 / 2 = 4,5
Расстояние же KN найдем по теореме Пифагора.
KN = √(4,52 + 62 ) = 7,5 см
Аналогично, найдем расстояние до второго катета:
OM = CB / 2 = 12 / 2 = 6
KN = √( 62 + 62 ) = √72 = 6√2 см
Ответ: 7,5 см, 6√2 см
0
Перпендикуляр к квадрату |
Описание курса
| Призма. Параллелепипед. Куб. Решение задач
ВИДЕОУРОК
Высота прямоугольного треугольника.
Высотой
прямоугольного треугольника называется перпендикуляр, опущенный из вершины
треугольника на противоположную сторону.
В прямоугольном
треугольнике высоты, опущенные из вершин острых углов, совпадают с катетами
треугольника, а высота, опущенная из вершины прямого угла на гипотенузу, делит
треугольник на два треугольника, подобных исходному и подобных друг другу.
Длина высоты
треугольника АВС
проведённой к гипотенузе ВС находится по формуле:
АК2 = ВК ∙ КС.
где ВК и КС – проекции катетов на гипотенузу.
В
прямоугольном треугольнике высота, опущенная из вершины прямого угла на
гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих
катетов:
В прямоугольном
треугольнике высота, проведённая из прямого угла, равна произведению катетов,
делённому на гипотенузу.
Каждый катет
прямоугольного треугольника есть среднее пропорциональное между гипотенузой и
отрезком гипотенузы, заключённым между катетом и высотой, проведённой из
вершины прямого угла.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Высоты ha и hb совпадают
с катетами b и a.
Отрезок XY есть среднее пропорциональное (или среднее
геометрическое) между отрезками АВ и СD, если
ЗАДАЧА:
В треугольнике АВС:
∠ С = 90°,
∠ А = 30°,
АВ = 2√͞͞͞͞͞3.
Найдите высоту СН.
РЕШЕНИЕ:
Начертим
чертёж.
Так как катет, лежащий против угла 30°, равен половине гипотенузы, то
ВС = 0,5АВ = √͞͞͞͞͞3.
Найдём катет АС в треугольнике АВС,
пользуясь теоремой Пифагора:
АВ2 = АС2
+ ВС2,
АС2 = АВ2
– ВС2 =
= (2√͞͞͞͞͞3)2 – (√͞͞͞͞͞3)2 =
=12 – 3 = 9, АС = 3.
В треугольнике АНС: АС –
гипотенуза, НС – катет, лежащий против угла
30°, значит
НС =
3 : 2 = 1,5.
ЗАДАЧА:
В треугольнике АВС:
∠ С = 90°,
∠ А = 30°,
СН – высота.
Найдите
АН, если АВ = 2.
РЕШЕНИЕ:
Начертим
чертёж.
Так как катет, лежащий против угла 30°, равен половине гипотенузы, то
ВС = 0,5АВ = 1.
Тогда
по теореме Пифагора из треугольника АВС:
Из прямоугольного треугольника АНС:
НС =
0,5АС = √͞͞͞͞͞3 : 2.
Тогда
по теореме Пифагора:
ЗАДАЧА:
В треугольнике АВС:
∠ С = 90°,
∠ А = 30°,
СН – высота.
Найдите
ВН, если АВ = 4.
РЕШЕНИЕ:
Начертим
чертёж.
Так как катет, лежащий против угла 30°, равен половине гипотенузы, то
ВС = 0,5АВ = 2.
Угол
ВСН равен 30° (90° – 60°),
значит
ВН = 0,5ВС = 1.
ЗАДАЧА:
В прямоугольном треугольнике АВС высота АК делит гипотенузу
на отрезки
ВК = 3 см,
КС = 2 см.
Найдите катеты
треугольника.
РЕШЕНИЕ:
Найдём квадрат длины высоты АК пользуясь формулой
АК2 = ВК ∙ КС = 3 ∙ 2
= 6.
Рассмотрим
прямоугольные треугольники АКС и ВКС, и найдём в них стороны АС и АВ.
Медиана прямоугольного треугольника.
Медиана – это отрезок, соединяющий вершину треугольника с
серединой противолежащей стороны.
Для прямоугольного треугольника это будут
медианы, проведённые с острого угла к серединам катетов или с прямого к центру
гипотенузы.
Свойства
медианы в прямоугольном треугольнике.
– медианы в прямоугольном треугольнике пересекаются в
одной точке, а точка пересечения делит их в соотношении два к одному считая от
вершины, из которой проведена медиана;
– медиана, проведённая из
вершины прямого угла к гипотенузе, равна половине гипотенузу;
– медиана, опущенная на гипотенузу прямоугольного треугольника, равна
радиусу окружности, описанной вокруг данного прямоугольного треугольника;
– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам
медианы, опущенной на гипотенузу;
– сумма
квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти
четвёртых квадрата гипотенузы;
– медиана,
опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов
катетов;
– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два синуса
противолежащего катету острого угла;
– медиана,
опущенная на гипотенузу, равна частному от деления длины катета на два косинуса
прилежащего катету острого угла;
– сумма квадратов сторон
прямоугольного треугольникаравна восьми квадратам медианы, опущенной на его
гипотенузу;
– медиана, проведённая к катету а, равна
половине корня квадратного из суммы учетверённого квадрата катета b и квадрата катета а;
– медиана, проведённая к катету b, равна
половине корня квадратного из суммы учетверённого квадрата катета а и квадрата катета b;
Обозначения в формулах.
a, b – катеты
прямоугольного треугольника;
с – гипотенуза
прямоугольного треугольника.
Если обозначить треугольник, как АВС, то
ВС = а, АС = b, АВ = с
(то есть стороны а,
b, с – являются
противолежащими соответствующим углам).
та –
медиана, проведённая к катету а;
тb – медиана,
проведённая к катету b;
тс –
медиана, проведённая к гипотенузе с;
α (альфа) –
угол САВ,
противолежащий стороне а.
ЗАДАЧА:
Две стороны треугольника равны 6 см и 8 см. Медианы, проведённые к этим сторонам, пересекаются
под прямым углом. Найдите третью сторону треугольника.
РЕШЕНИЕ:
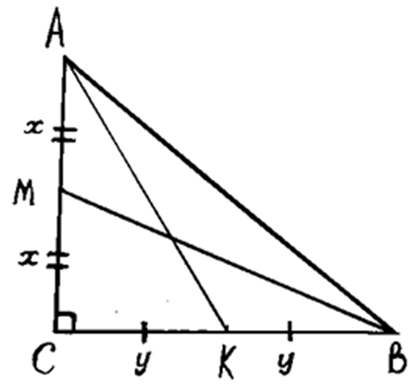
Начертим
чертёж.
Обозначим
АN = х см. ВМ
= у см.
Тогда
АО = 2/3 х,
NО = 1/3 у,
ВО = 2/3 х,
МО = 1/3 у.
АМ2 = ОМ2
+ ОА2,
ВN2 = ОВ2 + ОN2,
5х2 + 5у2 = 225,
х2 + у2
= 45.
АВ2 = ВО2
+ ОА2 =
= 4/9 (х2
+ у2) = 20, то
АВ = √͞͞͞͞͞20 = 2√͞͞͞͞͞5 см.
ЗАДАЧА:
В треугольнике АВС:
АВ = √͞͞͞͞͞41, ВС = 13,
ВН – высота, опущенная на
сторону АС, ВН = 5.
Найдите
длину медианы АМ.
РЕШЕНИЕ:
Начертим чертёж.
В прямоугольном
треугольнике ВНС по
теореме Пифагора
В прямоугольном
треугольнике АВН по
теореме Пифагора
Опустим из точки М перпендикуляр МD на сторону АС, МD – средняя линия треугольника ВНС, следовательно
МD = 1/2 ВН = 5/2,
НD = DС = 1/2 НС = 6.
Тогда в прямоугольном треугольнике АМD
∠ АDМ = 90°,
АD = АН + НD =
= 4 + 6 = 10,
МD = 5/2.
По теореме Пифагора
ЗАДАЧА:
В прямоугольном треугольнике медианы, проведённые к
катетам равны √͞͞͞͞͞52 и √͞͞͞͞͞73. Найдите длину
гипотенузы.
РЕШЕНИЕ:
Начертим чертёж.
Проведём медианы АК
и ВМ. Пусть
АК = √͞͞͞͞͞52,
ВМ = √͞͞͞͞͞73,
х – половина длины
стороны АС,
у – половина длины
стороны ВС. Тогда из
прямоугольных треугольников АСК и ВСМ имеем:
АК2 = АС2
+ СК2,
ВМ2 = МС2
+ ВС2
тогда составим систему уравнений:
отсюда
5(х2 + у2) = 125,
х2 + у2
= 25,
АК2 = 4(х2
+ у2).
АВ = 10.
ЗАДАЧА:
Медианы СМ и
ВN прямоугольного
треугольника АВС (∠ С = 90°), перпендикулярны. Найдите катеты, если гипотенуза
равна с.
РЕШЕНИЕ:
Начертим чертёж.
МА = МС = МВ = с/2.
Пусть NО = х,
Тогда
ВО = 2/3 х, МО = с/6.
МВ2 = МО2 + ВО2,
Биссектриса прямоугольного треугольника.
Биссектрисою прямоугольного треугольника называют отрезок
биссектрисы угла треугольника, который соединяет его вершину с точкой на противоположной
стороне треугольника.
Биссектриса прямоугольного треугольника делит противоположную сторону на
отрезки, соответственно пропорциональные двум другим сторонам.
Связь угла (α) между
высотой и биссектрисой, проведёнными из прямого угла, определяется через острые
углы этого треугольника.
ЗАДАЧА:
Биссектриса прямого угла
прямоугольного треугольника образует с гипотенузой углы, один из которых
равен 70°. Найдите острые углы этого треугольника.
РЕШЕНИЕ:
Начертим чертёж.
∠ DBC = ∠ DBA = 45°,
∠ DCB = 180° – 70° – 45° = 65°,
∠ ADB = 180° – 70° = 110°,
∠ CAB = 180° – 110° – 45° = 25°.
ЗАДАЧА:
Биссектриса прямого угла
прямоугольного треугольника делит гипотенузу на отрезки длиной 15
см и
20
см. Найдите длины отрезков гипотенузы, на которые её делит высота треугольника.
РЕШЕНИЕ:
Биссектриса треугольника делит сторону на
отрезки, пропорциональные прилежащим сторонам.
Следовательно,
СВ
: АС = 15 : 20.
Пусть коэффициент этого
отношения будет х. Тогда
АС = 20х, ВС
= 15х,
АВ = 20 + 15 = 35.
По теореме Пифагора:
АС2 + ВС2 = АВ2,
400х2
+ 225х2 = 1225.
х = √͞͞͞͞͞1,96 = 1,4,
АС = 20 ∙ 1,4 = 28,
ВС = 15 ∙ 1,4 = 21.
Катет прямоугольного треугольника есть среднее
пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между
катетом и высотой.
ВС2 = АВ ∙ ВН,
441 = 35 ∙ ВН,
ВН
=
12,6,
АН = 35 – 12,6 =
22,4.
ЗАДАЧА:
Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.
РЕШЕНИЕ:
Начертим чертёж.
Так как связь угла (α) между высотой и биссектрисой, проведёнными из
прямого угла, определяется через острые углы этого треугольника следующим
образом:
∠ ВАС
= 45° – α,
∠ ВСА
= 45° + α,
∠ α = ∠ МВD = 14°,
то меньший угол
треугольника ВАС будет равен:
∠ ВАС = 45° – 14° = 31°.
Задания к уроку 9
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Точка и прямая
- Урок 2. Угол
- Урок 3. Параллельные и перпендикулярные прямые
- Урок 4. Окружность
- Урок 5. Угол и окружность
- Урок 6. Треугольник (1)
- Урок 7. Треугольник (2)
- Урок 8. Прямоугольный треугольник (1)
- Урок 10. Равнобедренный треугольник (1)
- Урок 11. Равнобедренный треугольник (2)
- Урок 12. Периметр треугольника
- Урок 13. Периметр равнобедренного (равностороннего) треугольника
- Урок 14. Треугольник и окружность
- Урок 15. Прямоугольный треугольник и окружность
- Урок 16. Равнобедренный треугольник и окружность
- Урок 17. Четырёхугольники
- Урок 18. Параллелограмм
- Урок 19. Периметр параллелограмма
- Урок 20. Прямоугольник
- Урок 21. Периметр прямоугольника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеция
- Урок 26. Равнобедренная трапеция
- Урок 27. Периметр трапеции
- Урок 28. Четырёхугольник и окружность (1)
- Урок 29. Четырёхугольник и окружность (2)
- Урок 30. Многоугольник
- Урок 31. Правильный многоугольник
- Урок 32. Осевая и центральная симметрии
Высота в прямоугольном треугольнике
Вспомним определение. Высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:
sin A
cos A
Высота проведена к гипотенузе AB. Она делит треугольник на два прямоугольных треугольника —
и
. Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит,
, то есть угол
равен углу
. Аналогично, угол
равен углу
.
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника
(и треугольника
). Треугольники
и
называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и
. Стороны треугольника
длиннее, чем стороны треугольника
в
раз:
Мы доказали свойство высоты прямоугольного треугольника. Его можно сформулировать как теорему.
Теорема 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, делит треугольника на три подобных друг другу треугольника:
При решении задач нам пригодится равенство углов треугольников и
, а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника
можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту. В геометрии это называется «метод площадей» и часто применяется в решении задач.
Задача 1.
В треугольнике ABC угол C равен CH — высота, BC = 3, cos A =
Найдите AH.
Решение:
Рассмотрим треугольник ABC. В нем известны косинус угла A и противолежащий катет BC. Зная синус угла A, мы могли бы найти гипотенузу AB. Так давайте найдем sin A:
sin + cos
= 1.
Эта формула – основное тригонометрическое тождество. Конечно, вы его знаете:
sin
sin
sin A (поскольку значение синуса острого угла положительно).
Тогда:
Рассмотрим прямоугольный треугольник ,
. Поскольку
Отсюда
Ответ:
Задача 2.
В треугольнике ABC угол C равен 90 AB = 13, tg A
. К гипотенузе проведена высота CH. Найдите AH.
Решение:
Это чуть более сложная задача. Ведь вам неизвестны катеты a и b.
Запишем теорему Пифагора: (1)
Нам известно также, что:
tg A (2)
Решая уравнения (1) и (2), найдем:
Запишем площадь треугольника AВС двумя способами:
и найдем длину .
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений, как в алгебре.
Теорема 2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна произведению катетов, деленному на гипотенузу.
Доказательство:
Из прямоугольного треугольника ABC с прямым углом C и гипотенузой AB:
sin
Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:
sin
Мы разными способами вычислили синус одного и того же угла. Приравняем полученные выражения:
Найдем высоту:
Что и требовалось доказать.
Задача 3. Катеты прямоугольного треугольника равны 15 и 20.
Найдите высоту, проведенную к гипотенузе.
Решение:
Воспользуемся теоремой 2 о высоте прямоугольного треугольника:
Катеты BС и AС нам известны: BC = 15, AC = 20. Найдем гипотенузу AB с помощью теоремы Пифагора:
Найдем высоту, проведенную из вершины прямого угла:
Ответ: 12.
Теорема 3. В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу.
Сейчас мы докажем эту полезную формулу.
Вспомним, что такое проекция точки на прямую. Например, из точки С опускаем СН — перпендикуляр к прямой AВ. Точка Н и будет проекцией точки С. Тогда AН – проекция катета AВ, а BН – проекция катета BС.
Обозначим:
Доказательство проведем двумя способами.
Первый способ доказательства:
Из прямоугольного треугольника BНС с прямым углом Н и гипотенузой BС:
tg
Из прямоугольного треугольника AНС с прямым углом Н и гипотенузой AС:
ctg
Заметим, что угол CBН – это угол CBA, а угол CAН – это угол BAC. Тогда:
tg
tg
Мы воспользовались тем, что тангенс и котангенс двух разных острых углов прямоугольного треугольника равны друг другу. Это следует из определения тангенса и котангенса.
Преобразуем получившееся выражение:
Что и требовалось доказать.
Второй способ доказательства:
Воспользуемся подобием треугольников, о которых говорится в теореме 1.
Рассмотрим пару прямоугольных треугольников AНC и BНC. Как было показано выше, эти треугольники подобны по двум углам, поэтому
Мы получили такое же соотношение, как и в первом способе доказательства.
Далее аналогично получим, что
Что и требовалось доказать.
Задача 4. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH = 4, BH = 16. Найдите длину CH.
Решение:
Воспользуемся теоремой 3 о высоте прямоугольного треугольника:
Подставим данные задачи.
CH = 8.
Ответ: 8.
Разберем решения других задач ОГЭ и ЕГЭ по теме «Свойства высоты в прямоугольном треугольнике».
Задача 5. Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 50. Найти высоту, проведенную из вершины прямого угла и отрезки, на которые гипотенуза делится высотой.
Решение:
Рассмотрим прямоугольный треугольник ABС с гипотенузой AB. Проведем высоту CD=h.
Учитывая отношение катетов, обозначим их длины как: BC = 3x, AC = 4x.
Тогда по теореме Пифагора получим:
По условию гипотенуза AB = 50. Следовательно, х = 10, BC = 30, AC = 40.
Далее можно действовать разными способами. Например, так.
где по определению косинуса:
cos A cos B
Ответ:
Задача 6. В прямоугольном треугольнике ABC высота CD делит гипотенузу на отрезки AD = 3 см и BD = 2 см. Найти катеты треугольника.
Решение:
Найдем квадрат длины высоты с помощью теоремы 3:
Из прямоугольного треугольника ADC по теореме Пифагора найдем
см.
Из прямоугольного треугольника BDC по теореме Пифагора найдем
см.
Ответ: см и
см.
Задача 7. Точка D является основанием высоты, проведенной из вершины прямого угла C треугольника ABC к гипотенузе AB. Найдите AC, если AD=8, AB=32.
Указание:
Найдите отрезок BD = AB — AD, после чего задача сводится к предыдущей.
Длину высоты прямоугольного треугольника можно также найти, если известны гипотенуза и один из острых углов треугольника.
h = c sincos
= c sin
cos
Докажем эту формулу.
Рассмотрим прямоугольный треугольник ACD:
В то же время из треугольника AВC:
Таким образом, h = CD = AC cos = AB sin
cos
= c sin
cos
Аналогично, из треугольника BCD получим: h = CD = BC cos = AB sin
cos
= c sin
cos
Задача 8. В прямоугольном треугольнике гипотенуза равна 10, а один из острых углов 15 градусов. Найти высоту, проведенную из вершины прямого угла.
Решение:
Воспользуемся доказанной выше формулой:
h = c sincos
= 10 sin
cos
= 5sin
= 2,5.
Ответ: 2,5.
Задача 9. Высота прямоугольного треугольника делит его гипотенузу на отрезки 6 см и 4 см. Найдите площадь этого треугольника.
Решение:
Гипотенуза прямоугольного треугольника равна сумме данных отрезков:
см.
Найдем высоту, проведенную из вершины прямого угла к гипотенузе: см.
Площадь треугольника:
см
Ответ: см
Если вам понравился наш материал — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Высота в прямоугольном треугольнике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Как найти перпендикуляр в треугольнике
В геометрии одна задача может скрывать в себе множество подзадач, требующих от решающего их человека наличия большого количества знаний. Так для операций с треугольниками, нужно знать о соотношениях между медианами, биссектрисами и сторонами, уметь разными способами вычислять площадь фигур, а также находить перпендикуляр.

Инструкция
Обратите внимание на то, что перпендикуляр в треугольнике необязательно должен лежать внутри фигуры. Высота, опущенная на основание, может оказаться и на продолжении стороны, как это происходит в том случае, если один из углов больше девяноста градусов, или совпадать со стороной, если треугольник прямоугольный.
Воспользуйтесь формулой для вычисления высоты треугольника, если задача содержит все требуемые для этого данные. Для нахождения перпендикуляра составьте дробь, в числителе которой удвоенный квадратный корень из следующего произведения: р*(р-а)(р-в)(р-с), где а, в и с – стороны треугольника, а р – его полупериметр. В знаменателе дроби должна стоять длина того основания, на которое опущен перпендикуляр.
Найдите высоту треугольника, воспользовавшись формулой для вычисления площади этой фигуры: для этого достаточно удвоенную площадь поделить на длину основания. Для нахождения площади используйте другие формулы: например, найти эту величину можно через полупроизведение двух сторон треугольника на синус угла между ними.
Запомните основное соотношение между высотами треугольника: оно обратно пропорционально отношению оснований. Также выучите стандартные формулы, позволяющие быстро найти перпендикуляр в равностороннем и равнобедренном треугольнике. В первом случае высота являет собой произведение стороны треугольника на синус угла в 60 градусов (как следствие формулы для вычисления площади), во втором – удвоенному корню из разности квадрата двойной длины боковой стороны и квадрата основания.
Посчитайте перпендикуляр треугольника, введя данные в графы онлайн-калькулятора. Для этого вам необходимо знать длины сторон данной фигуры, так как расчет проводится по первой указанной выше формуле, использующей полупериметр.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.