Как найти длину пирамиды хеопса

                    Глава I. Пирамиды Хеопса как
первое Чудо Света     

§1.Что называется первым
Чудом Света?

   Пирамида Хеопса (Хуфу), Великая пирамида
Гизы — крупнейшая из египетских пирамид, единственное из «Семи чудес света»,
сохранившееся до наших дней.  Пирамида Хеопса входит в комплекс самых крупных
египетских пирамид, расположенных на плато Гиза. Это — пирамиды Хеопса (Хуфу),
Хефрена (Хафра) и Микерина (Менкаура). Архитектором Великой пирамиды считается
Хемион, визирь и племянник Хеопса. Он также носил титул «Управляющий всеми
стройками                                                                        
фараона». Более трёх тысяч лет (до постройки кафедрального собора в Линкольне,                                                                                         

Англия, около 1300 года) пирамида
являлась самой высокой постройкой на Земле.                                           
                                        

  Предполагается, что строительство,
продолжавшееся двадцать лет, закончилось около 2540 года до н. э. Существующие
методы датирования времени начала строительства пирамиды делятся на
исторические, астрономические и радиоуглеродные. В Египте официально
установлена и празднуется дата начала строительства пирамиды Хеопса — 23
августа 2560 года до н. э. Данная дата получена с использованием
астрономического метода Кейт Спенс (Университет в Кембридже). Однако не стоит считать
эту дату истинным историческим событием, так как её метод и полученные с его
помощью даты подвергались критике многих египтологов. Существующие три других
метода датирования дают разные даты — Стивена Хака (Университет Небраска) 2720
до н. э., Джуана Антонио Бельмонте (Университет астрофизики в Канарисе) 2577 до
н. э. и Поллукса (Университет Баумана) 2708 до н. э. Радиоуглеродный метод даёт
диапазон от 2680 до н. э. до 2850 до н. э. Поэтому установленному «дню
рождения» пирамиды нет никаких серьёзных подтверждений, так как египтологи не
могут сойтись в том, в каком именно году началось строительство.

   Несмотря на различные, порой
диаметрально противоположные взгляды

на природу данного феномена, к ней
всегда будут обращаться исследователи. Люди, живущие в разные эпохи, имеющие
различное образование и интересы не могли и, наверное, никогда не смогут
равнодушно смотреть на это чудо. Пирамида Хеопса является одним из самых
изучаемых объектов материальной культуры, оставшейся нам от прежних
цивилизаций. Одним

из самых изучаемых и одним из самых
измеренных. Многие исследователи прошлого были твердо уверены в том, что в
Великой пирамиде в зашифрованном виде сохранились древние знания. Возможность
постичь логику формообразования пирамиды Хеопса значило для них получить некий
ключ к знаниям, которые были забыты или утрачены. Откуда взялась эта
уверенность? Что, в принципе, можно зашифровать в размерах пирамиды? Что могут
значить несколько цифр? Длина основания, высота, апофема, площади, отношения
достаточно хорошо изучены. В литературе они выражаются в метрической системе, в
дюймах, парижских футах и туазах, в «королевских» локтях и так далее. Однако
большинство исследователей обращает внимание на отношения, которые возникают
при сопоставлении основных параметров пирамиды Хеопса, считая, что только
безразмерные отношения смогут нам что-то подсказать.

   Из-за своих огромных размеров ее
иногда называют Большой пирамидой и помещают первой в списке чудес света. Если
не считать Великой Китайской стены, то пирамида Хеопса — самое большое
сооружение, когда-либо воздвигнутое человеком.

§2. История возникновения пирамиды Хеопса

  Юный фараон Хеопс отдал приказ о строительстве
пирамиды сразу же после смерти своего отца Снофру. Как и все предыдущие фараоны
со времен Джосера (примерно 2609 -2590 до Р. Хр.), Хеопс хотел быть погребенным
после своей смерти в пирамиде.

  Высота пирамиды составляет 146,6 м, что примерно
соответствует пятидеся- тиэтажному небоскребу. Площадь основания составляет
230х230 м. На таком пространстве свободно могли бы поместиться одновременно
пять крупнейших соборов мира: собор святого Петра в Риме, собор святого Павла и
Вестминстерское аббатство в Лондоне, а также флорентийский и миланский соборы.
Из строительного камня, пошедшего на возведение пирамиды Хеопса, можно было бы
построить все церкви Германии, созданные в нашем тысячелетии.

  Статуя фараона Хеопса из слоновой кости —
единственное сохранившееся изображение фараона. На голове Хеопса корона
Древнего Египетского царства, в руке церемониальное опахало.

  Как и его предшественники, он считал, что его
пирамида должна превосходить своими размерами, великолепием и роскошью все
другие пирамиды. Но прежде чем первый из более чем двух миллионов блоков, из
которых сложена пирамида, был вырублен в каменоломне на восточном берегу Нила,
были проведены сложные подготовительные работы. Сначала нужно было найти
подходящую площадку для строительства пирамиды. Вес огромного сооружения
составляет 6 400 000 тонн, поэтому грунт должен был быть достаточно прочным,
чтобы пирамида не ушла в землю под действием собственного веса.

  Строительную площадку выбрали южнее современной египетской
столицы Каир, на выступе плато в пустыне в семи километрах западнее селения
Гиза. Эта прочная скалистая площадка была в состоянии выдержать вес пирамиды.

Сначала выровняли поверхность площадки. Для этого вокруг
нее построили водонепроницаемый вал из песка и камней. В образовавшемся
квадрате вырубили густую сеть небольших каналов, пересекающихся под

прямым углом, так что площадка стала похожа на
огромную шахматную доску.

  Каналы заполнили водой, высоту
уровня воды обозначили на боковых стенках, затем воду спустили. Каменотесы
вырубили все, что выступало над гладью воды, и каналы вновь заложили камнем.
Основание пирамиды было готово.

  Свыше 4000 человек — художников, архитекторов,
каменотесов и прочих ремесленников — выполняли эти подготовительные работы
около десяти лет.

Лишь после этого можно было приступать к сооружению
самой пирамиды. Как сообщает греческий историк Геродот (490 — 425 г. до Р.
Хр.), строительство продолжалось еще лет двадцать, около 100 000 человек
трудилось над сооружением огромной гробницы Хеопса. Только на редис, лук и
чеснок, добавлявшиеся к пище строительных рабочих, было израсходовано 1600
талантов, т.е. приблизительно 20 млн. современных немецких марок.

   Данные о количестве рабочих подвергаются сомнению
многими современными исследователями. По их мнению, для такого количества людей
просто не хватило бы места на строительной площадке: более 8000 человек не
смогли бы производительно трудиться, не мешая друг другу. В период сооружения
пирамиды Египет был богатой страной. Ежегодно с конца июня до ноября Нил
выходил из берегов и заливал своими водами прилегающие поля, оставляя на них
толстый слой ила, превращавшего сухой песок пустыни в плодородную почву.
Поэтому в благоприятные годы можно было снимать до трех урожаев в год — зерно,
фрукты и овощи. Итак, с июня по ноябрь крестьяне не могли трудиться на своих
полях. И они были рады, когда каждый год в середине июня в их деревне появлялся
писец фараона, составлявший списки желающих работать на строительстве пирамиды.

Почти все желали этой работы, а значит, она была не подневольным,
а добровольным трудом. Это объяснялось двумя причинами: каждый участник строительства
во время работы получал жилье, одежду, питание и скромное жалованье. Через
четыре месяца, когда воды Нила сходили с полей, крестьяне возвращались в свои
деревни. Кроме того, каждый египтянин считал своим естественным долгом и делом
чести участвовать в сооружении пирамиды для фараона. Ведь всякий, кто вносил
свою лепту в выполнение этой грандиозной задачи, надеялся, что и его коснется
частица бессмертия богоподобного фараона. Поэтому в конце июня нескончаемые
потоки крестьян устремлялись в Гизу. Там их размещали во временных бараках и
объединяли в группы по восемь человек. Можно было начинать работу.

  Переплыв на лодках на другой берег
Нила, мужчины направлялись в каменоломню. Там они вырубали каменную глыбу,
обтесывали ее с помощью кувалд, клиньев, пил и буравов и получали блок нужных
размеров — со сторонами от 80 см до 1,45 м. Используя канаты и рычаги, каждая
группа устанавливала свой блок на деревянные полозья и на них по бревенчатому
настилу перетаскивала его к берегу Нила. Парусная лодка переправляла рабочих и
блок весом до 7,5 тонн на другой берег.

  По выложенным бревнами дорогам камень доставляли
волоком на строительную площадку. Тут наступала очередь самой тяжелой работы,
поскольку краны и другие подъемные устройства еще не были изобретены. По
наклонному въезду шириной 20 м, построенному из кирпичей из нильского ила,
полозья с каменным блоком при помощи канатов и рычагов затягивали на верхнюю
площадку строящейся пирамиды. Там рабочие укладывали блок на указанное
архитектором место с точностью до миллиметра.

  Чем выше поднималась пирамида, тем длиннее и круче
становился въезд и все больше уменьшалась верхняя рабочая площадка. Поэтому работать
становилось все тяжелее. Затем наступала очередь самой опасной работы: укладки „пирамидона»
– верхнего блока высотой девять метров,

волоком затянутого наверх по наклонному въезду.

  Сколько человек погибло, выполняя
только эту работу, мы не знаем. Так через двадцать лет завершилось возведение
корпуса пирамиды, которая состоит из 128 слоев камня и на четыре метра выше Страсбургского
собора. К этому времени пирамида выглядела примерно так же, как она выглядит
сейчас: это была ступенчатая гора. Однако на этом работа не закончилась:
ступени были заложены камнями, так что поверхность

пирамиды стала хотя и не вполне гладкой, но уже без
выступов.

                                                                         
                   Пирамида Хеопса в XIX веке

 В завершение работ четыре треугольные внешние грани
пирамиды были облицованы плитами из ослепительно белого известняка. Края плит
были пригнаны так точно, что между ними невозможно было вставить даже лезвие
ножа. Даже с расстояния в несколько метров пирамида производила впечатление
гигантского монолита. Внешние плиты были отполированы до зеркального блеска с
помощью самых твердых шлифовальных камней. По свидетельству очевидцев, на
солнце или при лунном свете гробница Хеопса загадочно сверкала, как огромный светящийся
изнутри кристалл. » Однако пирамида Хеопса не состоит сплошь из
камня. Внутри нее находится разветвленная система ходов, которая через большой
ход длиной 47 м, так называемую большую галерею, ведет к камере фараона —
помещению длиной 10,5 м, шириной 5,3 м и высотой 5,8 м.

Она целиком облицована гранитом, но не украшена
никаким орнаментом. Здесь стоит большой пустой гранитный саркофаг без крышки.
Саркофаг был внесен сюда еще во время строительства, так как он не проходит ни
в один из ходов пирамиды. Такие камеры фараонов есть почти во всех египетских
пирамидах, они служили последним пристанищем фараона.

После смерти тщательно забальзамированное тело  властителя
помещали в погребальную камеру пирамиды.

Внутренние органы умершего помещали в специальные герметические
сосуды, так называемые канопы, которые ставили рядом с саркофагом в
погребальной камере. Итак, бренные останки фараона находили свое последнее
земное пристанище в пирамиде, а „ка» умершего покидало гробницу.
„Ка», по египетским представлениям, считалось чем-то вроде двойника
человека, его „вторым я», которое покидало тело в момент смерти и могло
свободно перемещаться между земным и загробным миром. Покинув погребальную
камеру, „ка» устремлялось на вершину пирамиды по внешней ее облицовке,
настолько гладкой, что никто из смертных не смог бы по ней передвигаться. Там
уже находился отец фараонов — бог солнца Ра в своей солнечной ладье, в которой
умерший фараон начинал свое путешествие в бессмертие.

    В последнее время некоторые ученые высказывают
сомнение в том, что

Большая пирамида действительно была усыпальницей
фараона Хеопса. В пользу такого предположения они выдвигают три аргумента:

• Погребальная камера, вопреки обычаям того времени,
не имеет никаких украшений.

• Саркофаг, в котором должно было покоиться тело
умершего фараона, лишь грубо отесан, т.е. окончательно не готов; крышка
отсутствует.

• И, наконец, два узких хода, по которым через
небольшие отверстия в корпусе пирамиды в погребальную камеру проникает воздух
снаружи. Но мертвые в воздухе не нуждаются — вот еще один весомый аргумент в
пользу того, что пирамида Хеопса не была местом погребения.

    Более 3500 лет внутренность Большой пирамиды не
была потревожена никем: все входы в нее были тщательно замурованы, а саму гробницу,
по представлениям египтян, охраняли духи, готовые умертвить каждого, кто
попытается проникнуть в нее.

   Вот почему грабители появились
здесь гораздо позже. Первый, кто проник внутрь пирамиды Хеопса, был халиф Абдалла
аль-Ма’мун (813 — 833 после Р. Хр.), сын Гаруна аль-Рашида. Он проложил туннель
к погребальной камере в надежде обнаружить там сокровища, как и в других
гробницах фараонов. Но не нашел ничего, кроме помета обитавших там летучих
мышей, слой которого на полу и на стенах достигал 28 см. После этого интерес
грабителей и искателей драгоценностей к пирамиде Хеопса пропал. Но на смену им
пришли другие расхитители. В 1168 г. после Р. Хр. часть Каира была сожжена и

 Наблюдение вогнутости сторон в конце XIX в.,

 Описание Египта

полностью разрушена арабами, не желавшими, чтобы она
попала в руки крестоносцев. Когда же потом египтяне принялись за восстановление
своего города, они сняли блестящие белые плиты, покрывавшие пирамиду снаружи, и
использовали их для постройки новых домов. Еще и сейчас эти плиты можно увидеть
во многих мечетях старой части города. От прежней пирамиды остался лишь
ступенчатый корпус — такой она предстает ныне перед восторженными взорами
туристов. Вместе с облицовкой пирамида лишилась также своей вершины,
пирамидона, и верхних слоев кладки. Поэтому сейчас ее высота уже не 144,6 м, а
137,2 м. Сегодня вершина пирамиды представляет собой квадрат со сторонами
примерно 10 м. Эта площадка в 1842 г. стала местом проведения необычных
празднеств. Прусский король Фридрих Вильгельм IV, известный своей любовью к
искусству, отправил в долину Нила экспедицию под руководством археолога Рихарда
Лепсиуса с целью приобретения древнеегипетских предметов искусства и других
экспонатов для создаваемого в Берлине Египетского музея (он был открыт в 1855
г.).

15 октября, в день рождения короля, Лепсиус в сопровождении
нескольких бедуинов поднялся на пирамиду и, как он сам сообщает, под
троекратные возгласы: „Да здравствует король!» водрузил на вершине

флаг с прусским орлом. Так же своеобразно Лепсиус
отметил и Рождество 1842 г. В Сочельник он зажег на верхней площадке Большой
пирамиды рождественские огни, а в камере фараона поставил в саркофаг Хеопса
молодую пальму, которую украсил небольшими подарками для участников экспедиции.
И какими бы странными и комичными ни казались нам эти церемонии сегодня, они
принесли неожиданный успех. После появления в газетах сообщения о прусском орле
на вершине пирамиды, воздвигнутой 4000 лет назад, интерес к величайшим
творениям древности, присущий до тех пор лишь духовной элите, стал достоянием
самых широких слоев общества. Праздничные торжества в Гизе заново открыли для
Германии Семь чудес света.

Глава II. Пирамида Хеопса как
математическая модель

§1. Геометрическая модель
пирамиды

  Все пирамиды покоятся на
платформах. Платформы (Дж.Х.Коул называет их вымосткой) имеют небольшую высоту
и выступают относительно облицовки на 30 – 40 см. Для пирамиды Хеопса этот
отступ составляет от 38 до 48 см. У всех пирамид сохранилось достаточное количество
облицовочных плит для замеров угла наклона облицовки, причем, многие плиты находятся
в приличном состоянии. У пирамиды Хеопса по углам платформы вбиты металлические
стержни (наверное, это сделали исследователи и/или археологи), что позволяет четко
видеть границу платформы. У остальных пирамид по углам видны раскопы, в которых

можно увидеть углы платформ и линию
соединения платформы и нижнего ряда блоков облицовки, правда, далеко не во всех
случаях. Часть углов сильно разрушена. Но и этого достаточно, чтобы убедиться в
том, что измерения размеров пирамид проводились, проводились по определенной
методологии и цифры вполне надежны.

В основном специалисты и
исследователи при анализе основных параметров пирамиды Хеопса используют
среднее значение стороны основания около 230, 36 метра. Высота принимается
около 146, 6 метра, апофема – 186,5 метра. В различных источниках можно встретить
незначительные отклонения от указанных значений. Угол наклона граней пирамиды 51°
50′ или 51° 51′.

В различных источниках встречается,
так называемая «математическая модель пирамиды Хеопса».

Математическая модель
пирамиды Хеопса

    Пирамида Хеопса построена в форме
правильной пирамиды с квадратом в основании. По данным точной реконструкции
(она была частично разобрана на камень местными жителями):

1. В основании: квадрат со сторонами
по 230,35 метров (b=230,35 м).

2. Высота пирамиды Хеопса: 146,71
метра (h=146,71 м).

3. Боковая грань пирамиды
представляет собой равнобедренный прямоугольный треугольник — угол при вершине
90°, два угла внизу — по 45°.

4. Всего треугольных граней 4
(естественно, т.к. в основании — квадрат).

5. Сложена пирамида из кубических
блоков известняка, самый большой из которых имеет длину ребра 1,5 метра.

6. Вероятно, первоначально, к вершине
пирамиды вели 210 ступеней.

Золотые сечения: Обозначим c длину
«лестницы», которую образует наклонная боковая грань пирамиды. По
теореме Пифагора:

c²=h²+(b/2)²~186,52 метра

(b/2)/c~0,618 — золотое сечение.

Позднее была замечена ещё одна
«золотая закономерность»: Площадь основания пирамиды относится к
площади всех 4-х боковых граней пирамиды в пропорции «золотого
сечения». Площадь боковой грани оказалась равна квадрату её высоты (bc/2 =
h²).

Большинство исследователей сходятся в
том, что длина стороны основания пирамиды, например, GF равна L = 233,16 м. Эта
величина отвечает почти точно 500 «локтям». Полное соответствие 500
«локтям» будет, если длину «локтя» считать равной 0,4663 м.

Высота пирамиды (H) оценивается
исследователями различно от 146,6 до 148,2 м. И в зависимости от принятой
высоты пирамиды изменяются все отношения ее геометрических элементов. В чем
причина различий в оценке высоты пирамиды? Дело в том, что, строго говоря,
пирамида Хеопса является усеченной. Ее верхняя площадка в наши дни имеет размер
примерно 10 м, а столетие назад она была равна 6 м. Очевидно, что вершину пирамиды
разобрали, и она не отвечает первоначальной.

В 1837 г. английский полковник Г.
Вайз измерил угол наклона граней пирамиды: он оказался равным a = 51°51′. Эта
величина и сегодня признается большинством исследователей. Указанному значению
угла отвечает тангенс (tg a), равный 1,27306. Эта величина соответствует
отношению высоты пирамиды АС к половине ее основания CB, то есть AC / CB = H /
(L / 2) = 2H / L.

И вот здесь исследователей ожидал
большой сюрприз! Дело в том, что если взять корень квадратный из золотой
пропорции √t , то мы получим следующий результат √t = 1,272. Сравнивая эту
величину с величиной tg a = 1,27306, мы видим, что эти величины очень близки
между собой. Если же принять угол a = 51°50′, то есть уменьшить его всего на
одну угловую минуту, то величина a станет равной 1,272, то есть совпадет с
величиной √t.  Следует отметить, что в 1840 г. Г. Вайз повторил свои измерения
и уточнил, что
значение угла a =51°50′.

Если принять сторону основания как 2,
то высоту

можно принять 1,2727…, и апофему –
1,6180…

Отношение высоты к апофеме равно
0,78615…

Угол наклона боковой грани составляет
51,8273° или

51° 51′

Первое условие Геродота «Площадь
боковой грани равна высоте пирамиды в квадрате»:

1*1,618… ≈ (1,2727…)²

Второе условие Геродота «Периметр
основания

пирамиды при делении на удвоенную
высоту дает π:

2*4 / 2*1,2727… ≈ 3,1428…

Статистические данные
пирамиды

    * Высота (начальная): 146,60 м
(по подсчетам) или 280 Королевских локтей (1 Королевский       локоть = 52,920
см)

    * Высота (сегодня): ≈ 138,75 м

    * Угол: 51° 50′

    * Длина боковой грани
(изначально): 230,33 м (по подсчетам) или около 440 Королевских локтей

     

Компьютерное моделирование пирамиды
Хеопса      пирамида Хеопса в разрезе

* длина боковой грани (сейчас): около
225 м

    * Длина сторон основания
пирамиды: юг — 230,454 м; север — 230,253 м; запад — 230,357 м;       восток —
230,394 м.

    * Площадь основания (изначально):
≈ 53 000 м² (5,3 га)

    * Площадь пирамиды: (изначально)
≈ 85 500 m²

    * Периметр: 922 м.

    * Общий объем пирамиды без вычета
полостей внутри пирамиды (изначально): ≈ 2,58 млн м³

    * Общий объем пирамиды, после
вычета всех известных полостей (изначально): 2,50 млн м³

    * Средний размер наблюдаемых
каменные блоков: 1,0 м в ширину, высоту и глубину (но       большинство имеет
прямоугольную форму.)

    * Средняя масса каменных блоков:
2,5 т

    * Самый тяжелый каменный блок: 15
т

    * Количество блоков: около 2,5
млн.

    * По подсчетам общий вес
пирамиды: около 6,25 млн тонн

                                            
                                Рисунок 1компьютерное моделирование пирамиды Хеопса

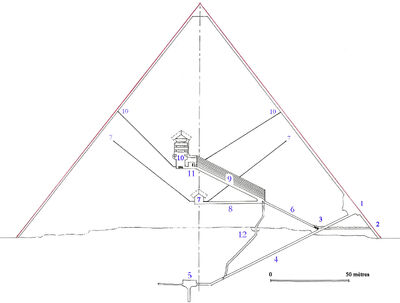
      Рассмотрим вопрос о строении
пирамиды. Пирамида имеет внутри три камеры: первая камера вырублена в скале на
глубине 30 м ниже основания и не совсем точно посередине; вторая расположена в
ядре пирамиды точно под вершиной на высоте приблизительно 20 м над основанием,
и третья камера расположена на высоте 42,3 м над основанием немного южнее от
оси пирамиды (см. рис.2).

В основе Великой пирамиды Хеопса
лежит скала высотой приблизительно 8,2 метра. Периметр Пирамиды, находящийся на
гранитной поверхности, идеально выровнен и представляет собой идеальный
квадрат.

Первоначальный вход расположен на
северной стороне на высоте 25 метров над основанием. Узкий туннель ведет вниз
под углом 26⁰31′ к нижней камере. На некотором расстоянии от входа
начинается другой туннель, ведущий к верхней камере под тем же самым углом, что
и первый. Далее туннель переходит в Большую Галерею длиной 47 метров (см. рис.
2). Рисунок 2 – Пирамида Хеопса в разрезе

Нахождение этих размеров осложняется
тем, что результаты измерения стандартным метром параметров древнейших объектов
всегда оказываются дробными. И это при всеобщем убеждении, что древние египтяне
не были знакомы с дробями. И пока не будет найдена гармония пропорциональных
взаимосвязей ее характерных размеров, невозможно даже приблизиться к разгадке
тайн пирамид.

.

 Рисунок 3 – Схема совмещения двойного квадрата и
пирамиды Хеопса в разрезе

 

Рисунок 4 – Схема построений для определения
положения средней камеры.

Остается невыясненным, из каких
построений мы получаем вершину К пирамиды.    

При выполнении этого соотношения
площадь грани пирамиды равна квадрату ее высоты. Именно этим равенством
площадей Геродот определял пропорции пирамиды Хеопса.                                                          

Для определения целочисленных
значений характерных размеров пирамиды Хеопса необходимо знать, какой системой
мер пользовались египтяне при постройке пирамиды. Английский исследователь
профессор Том выдвинул идею о существовании «стандартной» единицы измерения,
принятой в древнем мире. Он назвал ее «мегалитическим ярдом», равной 2,72 фута
или 0,829 м. Эту величину он получил на основе многочисленных измерений
характерных размеров древних сооружений, которые датируются 4700 –
3700 годами до н.э. на Пиренейском полуострове и на Британских островах.

На рис. 6 представлены основные
размеры пирамиды Хеопса в мегалитических ярдах, а схема, по которой древние
египтяне строили эту пирамиду, представлена на рис. 4.Поэтому, задавшись
известными размерами пирамиды Хеопса, приведем их к целочисленным значениям
размеров, взятых в мегалитических ярдах (м.я.). Тогда размер истинного
основания пирамиды составит 336 м.я., что соответствует 278,544 м. Отсюда можно
получить характерные размеры пирамиды Хеопса (см. рис. 6).

Рисунок 6 – Размеры пирамиды Хеопса

(размеры даны в мегалитических ярдах)

 Изучив литературу по данной теме мы
пришли к выводу,

что основополагающей всё живое
создано в соответствии с пропорцией, и именно таковыми являются пропорции
Великой Пирамиды. А благодаря тому, что человек, Земля, Солнечная Система и вся
Вселенная созданы в согласии с законом золотого сечения, то в пирамиде можно
найти и их параметры. В результате мы получили основные размеры пирамиды Хеопса
через золотое сечение с использованием древних мер длины – мегалитических ярдов
(м.я.). При этом высота пирамиды равна 212 м.я., что соответствует 175,748 м, а
высота наземной части равна 177 м.я. или 146,733 м, тогда длина основания
наземной части пирамиды равна 280 м.я. или 232,12 м, высота пирамиды Хеопса
увеличилась на 30 м и стала равна 175,7 м.,( высоты всех  пирамид исчислять не
от поверхности земли, а от основания нижних камер.)Расчеты ученых показывают,
что параметры трех главных пирамид и других, находящихся на плато Гизы
(проектная высота, углы наклона, периметр, взаимное расположение) связаны друг
с другом. 

§2. Конструирование пирамиды
по собственным расчетам

Изготовление пирамид

Изготавливается домашняя пирамида из
природного материала (доски, картона, оргстекла, плоского шифера, фанеры и
т.п.), обладающего диэлектрическими (изоляционными) свойствами, без единого
гвоздя и без применения прочих металлов, которые своим полем вносят искажения в
поле пирамидального пространства. Энергия этого пространства должна быть
чистой, без всяких искажений, тогда целебные свойства пирамиды будут
максимальны. Пирамида – это многогранник, основанием которого служит
многоугольник, а боковыми гранями являются  треугольники, имеющие общую
вершину. В основании правильной пирамиды всегда лежит правильный многоугольник
(например, для четырехгранной пирамиды – квадрат), а боковые грани –
равнобедренные треугольники, равные между собой. Кроме высоты характеристиками
пирамиды служат длина основания и высота боковой грани (апофема) пирамиды.

Домашняя пирамида может иметь любые
размеры, но соотношение ее высоты и длины основания должно быть строго
определенным, а именно: длина основания должна превышать высоту пирамиды в 1,6
раза. Такое соотношение соответствует пропорции золотого сечения, или
гармоничного деления. Таким образом, умножив заданную высоту пирамиды на 1,6 мы
получим длину ее основания. Для определения высоты боковой грани (апофемы
пирамиды) необходимо заданную высоту пирамиды умножить на 1,35. Одно из ребер
пирамиды должно быть сориентировано с помощью компаса строго на север.

Следует помнить, что с удвоением
высоты пирамиды активность ее действия возрастает во много (50-100 и более)
раз. Следовательно, если позволяет возможность, устанавливайте пирамиды с
максимальной высотой.

Размеры домашней пирамиды:

Высота	Длина основания	Ширина
1,7см	2*5=10	2*3,5=7
1,7	6*5=30	6*3,5=21
1,7	10*5=50	10*3,5=35
1,7	14*5=70	14*3,5=49
1,7	18*5=90	18*3,5=63
1,7	22*5=10	22*3,5=77

В начале, мы взяли 100 спичечных
коробков. После чего сделали прямоугольник размером: 1*2 коробка.

Затем сделали тот же прямоугольник,
но длиной 2*3 коробка.

Такую же операцию мы проделали
размером 3*4

И еще один раз, только размером 4*5

И наконец последнюю, размером 5*6

В итоге мы получили, вот такую
симпатичную пирамиду

Заключение

   Основополагающей константой в архитектуре, живописи и науке является
золотое сечение. Все живое создано в соответствии с пропорцией золотого
сечения, и именно таковыми являются пропорции Великой Пирамиды. А благодаря
тому, что человек, Земля, Солнечная Система и вся Вселенная созданы в согласии
с законом золотого сечения, то в пирамиде можно найти и их параметры. В
результате мы получили основные размеры пирамиды Хеопса через золотое сечение с
использованием древних мер длины – мегалитических ярдов (м.я.). При этом высота
пирамиды равна 212 м.я., что соответствует 175,748 м, а высота наземной части
равна 177 м.я. или 146,733 м, тогда длина основания наземной части пирамиды
равна 280 м.я. или 232,12 м, высота пирамиды Хеопса увеличилась на 30 м и стала
равна 175,7 м.,( высоты всех  пирамид исчислять не от поверхности земли, а от
основания нижних камер.) Расчеты ученых показывают, что параметры трех главных
пирамид и других, находящихся на плато Гизы (проектная высота, углы наклона,
периметр, взаимное расположение) связаны друг с другом. 

   Конструкция Великой
Пирамиды основана на пропорции Ф = 1,618. Архитекторы Пирамиды воплотили в
камне основополагающие принципы  геометрии:  

»        Периметр
основания пирамиды Хеопса, делённый на удвоенную высоту даёт приближение числа
«Пи» — 3,1415…(921,45/2*146,6=3,142).

»        Периметр
основания пирамиды равен длине окружности, радиус которой равен высоте пирамиды
(2*3,14159*146,6=921).

»        Длина
стороны основания, выраженная в египетских «локтях» (одно из значений
— 0,635 м), соответствует продолжительности земного года (230/0,63=365).

»        Сумма
четырёх сторон пирамиды — 921,45 метра равна половине минуты широты экватора.
Один градус широты на экваторе покрывает 110573 м, а каждая дуговая минута —
1842,88 м, что вдвое больше периметра пирамиды.

»        Если
умножить изначальную высоту Великой Пирамиды — 146,6 м на один миллион,
получается наименьшее расстояние от Земли до Солнца — 147000000 км (перигелий).

»        Соотношение
изначальной высоты Великой пирамиды к ее основанию равнялось 7:11. Это
соотношение имеет ряд важных геометрических свойств. В нем скрыты числа
«Пи» и «Ф».

Площадь каждой из
граней пирамиды равна квадрату ее высоты.

»        Длина
грани пирамиды, делённая на высоту, даёт соотношению Ф = 1,618.

»        Верхняя
северная и нижняя южная шахты построены по диагоналям прямоугольников,
описанных вокруг пирамиды.

               
Явным подтверждением необъяснимо высоких знаний египтян в области астрономии и
инженерно-строительного дела является расположение пирамиды Хеопса. Как
показывают исследования, боковые грани пирамиды ориентированы по сторонам
света, причем одна из них почти безошибочно указывает на истинный север.

    По нашим
исследованиям отмечается, что Пирамида Хеопса является пирамидой, построенной 
в отношении Золотого сечения. Таким образом, мы достигли цели исследования и
подтвердили гипотезу. 

Исследуя проблему
влияния пирамид на живую природу, становится очевидным, что пирамиды влияют на
живую природу Феноменальные свойства пирамид, как правило, увязывают с
геометрической формой, которая должна соответствовать закону «золотого
сечения». Оказывается, что это соотношение имеет единственное численное
выражение 1,618033988:= Ф, которое в виде инвариантов проявляется повсеместно в
природе (биологии, медицине, архитектуре, строительстве и т. д.).

Данная работа будет
полезна учащимся при изучении соответствующих разделов по геометрии. Ее можно
использовать и при заключительном повторении математики (повторить пропорции,
правильные пирамиды, диаграммы), на факультативных занятиях и кружковой работе
со старшими школьниками.

Список использованной
литературы

1.»Семь чудес света» — Ганс
Райхардт, 1996 г.

2.Большой энциклопедический словарь.
М. — 1988 г.

3.Бабанин В.П. Тайны великих пирамид.
С-Пб.: Лань, 1999. – 510 с.

4.Боннар А. Греческая цивилизация. —
М., 1958.

5. Замаровский В. Путешествие к
семи чудесам света. — М., 1980.

6. Ионина И.А. Сто великих
чудес. — М.: Вече, 2000.

7. Материал сайта о «Старых семи
чудес света» — http://www.vash-mir.ru

8. Материал о «Новых семи чудес
света» — http://www.@NEW7WONDERS.ru

9. Нейхард А.А., Шишова И.А. Семь
чудес света. — М.: Наука, 1966

10.Турскова Т. Великие сооружения
древнего мира. – М.: РИПОЛ КЛАССИК,  2002. – 416 с.

11.Черняк В.З. Семь чудес и другие. —
М.: Знамя, 1983.

12.Электронная версия энциклопедии
Кирилл и Мефодий. — http://www.km.ru

13.http://egpyram.narod.ru/info1.html

14.
http://orda2000.narod.ru/chrono/facts.htm#2

15.http://www.progulka.ru/znatoki/200202/13.html

Начало здесь…

И так читатель, мы условились в предыдущей публикации спроектировать макет пирамиды Хеопса высотою  равной “росту тещи”. Но здесь, как и в предыдущей публикации, у человека может вызвать скептицизм такая “легкомысленная” (шутливая) постановка задачи — “тещин рост и пирамида”. Но это грубейшая ошибка нашей логики возникшая из-за неумения работать с циркулем и Крестом (никто ведь и не учил этому) в крестцовой Мере.

Второе. Изменение единицы построения пирамиды (ниже) делается с целью продемонстрировать Великую Симметрию Пирамиды и главное понять, что значит такая симметрия и “золотые пропорции”?  И расшифровать, через Крест и Циркуль великое Послание древнего Востока заложенное в пирамиде  фараоном Хуфу

Доминантой тут является то, что  пирамида Хуфу-Хеопса конгруэнтна, т.е. соизмерима только с Крестом и только через Крест лежащий в основании “чаши Соломона”, т.е. Православный. Это максима диктует тут уже и свои “правила поведения” нашей Логики при постижении структуры строения пирамиды Хуфу. Иной подход — тупик.

(конгруэнтность (лат. congruens (congruentis) соразмерный, соответствующий, совпадающий; геометрически: соразмерность, соответствие, совпадение).

Из этой парадигмы далее следует вывод, что оперируя Циркулем в крестцовых соотношениях (т.е. золотых), уже не важно, что вы берете в вашей логике построения за “единицу”. Важна конкретная физическая “протяженность” измеримая и представимая вами с помощью Циркуля и Креста. Т.е. умение “крестить”!

В случае с примером “теща”, т.е. с протяженностями непостижимых для измерения циркулем, очень легко и просто это сделать, с не меньшей, а с большей точностью, с помощью куска бечевки. Циркуль это “для бумаги”, но принцип циркуля на большей протяженности можно успешно применить с помощью “бечевки” и “отвеса”, а вернее умением пользоваться ими, как и циркулем.    

Смеющаяся пирамида

Из всего того, что я изложил в предыдущем посте и здесь про “тещу”, вытекает только один вывод, что при построении (вернее при проектировании) макета пирамиды Хеопса вы можете взять за Единицу построения любую “единицу”, да хотя бы длину хвоста вашей любимой кошки — результат будет тот же. Ваша пирамида, вернее ее модель будет СИММЕТРИЧНА пирамиде Хуфу, как модель, уменьшенная в строго определенных пропорциях, но которую мы не знаем в конечном виде. Мы считаем с одной стороны, что сама пирамида есть целое, как “Большая Единица”, а наша модель как ее симметрия – “маленькая единица”. Для их соизмерения вначале нам надо выявить внутреннюю симметрию самой пирамиды и понять ее, как эта симметрия выглядит, т.е. работает. Поменяв скажем “основание” и “высоту” пирамиды, как Единицы, местами. Можно менять и другие грани.

Но тут же возникает и встречный вопрос: как выверить такой результат? Что является здесь индикатором истины? Вот самые главные вопросы возникающие у читателя. Исчерпывающий ответ выглядит так: УГОЛ, еще точнее – 3 УГЛА и их тангенсы, как отношения катетов, указанных на рисунке в вершине пирамиды. Пирамида Хуфу, потому и есть строго предопределенное строение, которой вы не можете приписать свои “измерительные фантазии”, как это показано на таблице1. Пирамида смеется над такими фантазиями…

Есть и другая, оборотная сторона медали в таком ответе, то, что перед

ал нам Геродот:

“…площадь одной треугольной её грани равняется квадрату общей высоты Пирамиды”.

Эти аксиомы одновременно есть и максима, как “судия” между нами и истиной! Остается лишь один единственный вопрос: “а судьи кто?” в этом мире. Ответ: пирамида Хуфу. Она всех расставить “на место”!

Вера и Мера

У читателя может возникнуть вопрос (он и у меня возник вначале), если нам известно основание пирамиды (как я утверждаю), то почему бы теперь не перевести разговор в плоскость конкретики и не “дать размеры пирамиды” сразу?

Это было бы очень легко сделать читатель, но это было бы нравственное преступление с моей стороны перед Востоком и авторами пирамиды. Ибо важнее самой Истины – путь к ней. А именно ДОРОГА, что ведет к этой Истине, а она очень извилиста. В этом и заключена “тайна Хуфу”, с тем чтобы мы пошли ЕГО ПУТЕМ к постижению цели, а не доверяли греческим проходимцам от геометрии. И тем самим, мы сделали бы прорыв в нашем Мировоззрении.

Именно потому, когда строим циркулем пирамиду здесь и меняем местами “единицу”, то преследуется строго определенная цель. Первое, чтобы мы циркулем и линейкой (без деления, почему и взята абстрактная “теща” за единицу) не только научились откладывать пирамиду на бумаге, но и увидеть воочию  полученный физический результат  и ее описание на алгебраическом языке “золотых чисел”, о которых говорил О. Хайям.

Мы должны и увидеть, и убедиться, чтобы понять и научиться, как получать ФИЗИЧЕСКИ крестцовые значения на бумаге, как Основы Геометрии. А не продолжать нести греческую чушь о геометрии, которую они списали не поняв у Востока. Результаты таких “знатоков геометрии” в постижении тайны пирамиды Хуфу — приведены в сводной “табл. 1” ее автором. И эта таблица есть “сводное свидетельство” тому, насколько ничтожен наш ум перед величием Востока выраженное в этой пирамиде (и вам предстоит в этом убедиться).

Таблица 1

Сводная таблица замера пирамиды Хуфу. Автор: Сергей Проскуряков

Отсюда и задача наша: не “опустить” пирамиду Хеопса до нашего невежества, а напротив…

****

Давайте мы теперь  выявим математическую соразмерность, между пирамидой и нашей Мерой. Для этого найдем в пирамиде  Хуфу — ОСНОВАНИЕ, как логическое и метрическое “поле”, на которой возможны наши уроки измерения с циркулем далее. С тем чтобы возникающие при этом понятия – имели физический смысл еще.

Построение модели пирамиды, это как моделирование кораблей в домашних условиях. Главное здесь определить “класс” судов, скажем вы строите модель “эсминца”, а для этого вам надо знать строение остова корабля. Так и здесь… Потому мы выявим вначале этот “остов”, как сущность пирамиды Хуфу – “класс”. Т.е. несущую опорную конструкцию, к которой принадлежит пирамида Хеопса и ее особенности. Это как определение типа кораблей, каждая из которых имеет свой “примат”. Вернемся к рисунку пирамиды (рис.1 – это ее конечный вид):

Рис.1

Очевидно, что этот “остов” пирамиды составляет ее 1/8 часть (Рис. 2), которая несет в себе ВСЕ параметры строения пирамиды (Рис. 1). В данном случае  мы упрощаем не смысл, а содержание с тем, чтобы высветить ярче строение пирамиды, как сущность пирамиды — Хуфу. 

 Рис.2

Мы подразумевали именно этот “остов” в предыдущей публикации, с основанием равное “1”, которая равна “1/2, т.е. половине роста тещи”, как Единицы. Нам теперь надо, с помощью Креста ее нарисовать циркулем. Обратите внимание, что для этого надо построить “красный треугольник”, как основание “остова” тут, ибо IB перпендикулярно СВ и они равны тут –1, т.е. единице принятой нами. Давайте построим этот треугольник – основание “остова”:

Рис.2.1

При построении таких треугольников имейте в виду следующее, что задача эта и проста, и сложна. Само построение легко освоить, а вот отразить ее в нашем сознании уже труднее. Мы не привыкли к таким числам и пересечениям.  И так, что мы имеем как исходное физическое значение? Рост тещи – поделенное точно “пополам” – 1/2 роста ее. Это и есть Единица Основания.

1) Мы откладываем эту единицу на бумаге и циркулем “перекрестим” ее, чтобы получить Крест, как деление Единицы в золотых пропорциях:

1=f+f ²;

2) Отложим эту же Единицу на основание, перпендикулярно, как показано на рисунке – ОО₁;

3) Из перекрестия Креста отложим еще один раз саму единицу “вверх” так, чтобы у нас получился отрезок — f+1; т.е.:

1+f=F 

4) Если мы возьмем теперь этот отрезок – F, циркулем и из точки О₁ проведем такую прямую до пересечения перпендикуляра, то мы получим искомое значение равное “корень квадратный из F”! Как это показано на Рис. 2.1

Вот и все! Далее по остову (Рис.2) вы видите, что отрезок BI  равна также Единице и перпендикулярна к нашему полученному отрезку СВ=1. Отсюда уже аксиоматически получаются все остальные значения в нашем “остове”, как это показано на Рис.2. ВСЕ параметры “остова” далее, вытекают из этого треугольника и его численных значений. Убедитесь и, прежде всего, что вы понимаете этот процесс.

И мы тем самим дошли до самой критической точки или момента, который позволит нам понять Меру построения пирамиды Хуфу-Хеопса.

Потому этот остов и есть жестко заданная конструкция и принадлежность к пирамиде Хеопса определяется тем, что мы получаем равенство в соотношениях сторон нашей пирамиды с пирамидой Хеопса – Рис.1 и значений (тангенсов) ТРЕХ главных углов пирамиды на вершине ее.

Мы видим, что соотношение сторон выглядит так (параметры нашей модели, на Рис.2 напишем строчными буквами, а пирамиды Хеопса – Рис.1., заглавными, чтобы различать):

И далее ВСЕ соотношения нашей “единичной пирамиды” посвященные “теще”, должны совпадать с Мерой пирамиды Хуфу в тех же дробях ТОЧНО и с заданным конечным результатом. Равно, как и  новая пирамида, которую  мы построим еще, чтобы углубить наши знания по Геометрии  по этой пирамиде. Т.е. ВСЕ пирамиды (а их получится четыре), в которых казалось бы разные параметры сторон, как Единица, будут сводится к этому “остову” – с основанием Единицы — СИММЕТРИЧНО. Но важно заметить, что это не конгруэнтность Меры – т.е. “совпадение”, а только симметрия, что мы и выявили, с помощью циркуля. 

Пирамида, модель 2.

Если вы поняли принцип построения предыдущего “остова” пирамиды циркулем, то построение этого варианта будет восприниматься намного легче. Все решение этой задачи, а условие ее простое, заключается теперь в том, чтобы построить пирамиду уже высотою 1 единица. Неважно какой, напомню опять. Но мы договорились, что это будет полный рост “тещи” (а не половина). С тем, чтобы понять внутреннюю симметрию пирамиды, как предопределенность.

Ниже на картинке приведена вся премудрость построения и такой пирамиды – мне остается только поэтапно изложить “движение циркуля” в постижении такой Меры на Рис.3:

1) Есть 1, т.е. искомый “рост”, вы просто циркулем “крестите” ее и получаете два отрезка, как указано на рисунке3: f и f².

 Рис.3

2). Из “перекрестия” креста, циркулем, отложите 1, т.е. “рост” к горизонтальной линии, перпендикулярной к кресту – “ОО₁” – до их пересечения.

3). Соедините полученную точку “О₁” с вершиной креста и вы получите искомый “красный треугольник”, который и есть решение заданной задачи, со строго заданными параметрами, как единицы прямоугольного треугольника. В чем легко убедиться по “теореме Пифагора” на Рис.4.

Если проявить элементарное усилие над своим разумом, то легко построить далее уже сам “остов” с новыми параметрами которые приведены на рис.4

Рис.4

Отсюда становится понятно строение целой пирамиды с заданными параметрами и оно будет высотою “1 единица” равной Росту “счастливой тещи”! И теперь обратите внимание и убедитесь, что вы понимаете “тангенсы” этих углов и, что они не изменились.

Также убедимся и в равенстве площадей, о котором говорил Геродот (Рис.4):

И теперь сравним со структурой самой пирамиды (Рис.1), чтобы убедиться, что соотношение сторон остались в силе. Иначе и быть не могло:

Мы можем здесь построить и третью,  и четвертую модель пирамиды, когда апофема – АВ равна – 1. Равно, как модель в которой  угловая гран пирамиды: AI – равна той же «Единице”. Я делать этого не буду пока, но вам не возбраняется это делать самим. Потому как это осложнит постижение цели здесь. А потом, когда будем рассматривать смысл этих трех углов, я построю их и раскрою в чем смысл, как замысел авторов пирамиды. Ибо это очень важный момент. Но поверьте, а кто сможет проверьте,  т.е. постройте и убедитесь, что “от перемены мест единицы, углы не меняются”. Т.е. их катеты.

Количественная Мера пирамиды Хуфу

Итак, на Рис.1 мы имеем модель в которой основание равно половине “роста тещи” и мы ее приняли за Единицу. Но это ведь не значит, что и пирамида тоже имеет единицу “теща”. Мы  этот разговор вели к тому, что здесь в основании замысла авторов логически заложена известная истина: “Человек мера всех вещей” в этом мире. И они, т.е проектировщики пирамиды, учитывали именно эту мудрость, так сказать материализовали ее, когда закладывали “количества единиц”. И теперь, чтобы увидеть эту Единицу, мы должны вначале просчитать: а сколько  же единиц заложено в основании пирамиды Хуфу? Нам говорят “1000 локтей”, “500 локтей” и пр.

На самом деле протяженность основания квадрата Хеопса равна “единице” эквивалентной росту Одного человека, умноженной на 125. Значение 125 или 5³ имеет тут очень важное математическое, геометрическое и логическое значение. О чем мы поговорим позже.

Это означает теперь, что авторы отмерили основание пирамиды в виде квадрата, сторона которого равна – “125 раз по 1”, где искомая “1” нам еще неизвестна, но эквивалентна росту человека.

Но, если мы говорим о “человеческом измерении” (здесь подключается логика наша, при этих словах), то мы подразумеваем следующее: Коран учит (здесь это кстати) — “считай в паре”, что мы и сделаем, как это было раскрыто раннее и подробно, что рост человека есть значение – Ro, а его половина – есть единица — r или:

Ro=2r

Вот этот “r” и есть искомая единица, (пока логически). Это очень важно тут понять. Давайте упростим задачу до “арифметики” чтобы понять, что значит “125 человеков” здесь метрически означает? Представьте себе, что есть конкретный человек и его рост физически равен 1,8 метра. Если рост этого человека умножит на 125, получим – 225 метров. Вот эти условные 255 метров и есть общая сторона квадрата  в основании пирамиды.

Если мы теперь, строим “остов”, как 1/8 часть, то выявляется, что ее протяженность составляет –112,5 метров.

Вот эта протяженность 112, 5 метров по логике Хуфу выглядит так:

L=125×0,9 метр=125 х r

Тогда мы начинаем понимать. Ну например апофема в единичной пирамиде у нас равна – F. Но чему она будет равна при количественном измерении – “125 раз, по r”? Очевидно одно, что апофема имеет одно, единственное значение из Рис.1:

AB=125xFxr или 125 х F x 0,9метров;

Вот если бы мы точно знали, что “единица” равна – 0,9 метров, то мы могли бы нарисовать модель пирамиды Хуфу КОНГРУЭНТНУЮ самой пирамиде.

Давайте теперь нарисуем наш “остов” пирамиды проставив новые значения – “единицу – r” и количество “125 раз”, т.е. отложенных единиц. 

Рис.5

И теперь мы видим структуру пирамиды и ее масштаб. Зададимся вопросом, как бы мы построили модель пирамиды на земле, скажем в 10 раз меньшую, зная теперь единицу ее строения? Очевидно, мы бы вначале отложили саму единицу, как 1/2 общего основания пирамиды. А затем эту единицу отложили, скажем в виде кусочка бечевки. И затем еще “бечевки”, как “Меру Единицы” каждой из сторон остова. Потому как иначе нельзя.

Представьте себе пример единицы – 0,9 метра – здесь ясно. Но чему равна теперь длина веревки, которой мы замерим апофему например?

Ответ: 0,9 м х F=1,456230… метров

Также вычисляются и остальные единичные значения остова. Не числами, а “отмеривая” физически, что является более точным измерением. Мы должны понять и думать уже иначе, что мы не можем откладывать “метром” значения до тысячных долей, как у нас получилось. Эти значения можно и нужно только отмерить здесь, как я уже говорил “на земле” и “бечевкой”, как эталоны. Потому, други мои “рулетка”, как орудие Меры – не годится изначально. 

Речь может идти только о начале “закладки единицы” и для этого уже Тутанхамон оставил свой скипетр, как “начало”, как “Единицу”, чтобы это начало мы отложили – точно с тем, что в результате мы укажем и тем самим докажем и единицу измерения, и расчеты правильности расшифровки пирамиды Хеопса. Скипетр это не “палка”, а символ Меры, которую знают посвященные в нее люди. Строго избранные для этого. И этот скипетр хранится в музее Каира.

Вот только НИКТО этот скипетр которые века не может расшифровать. Здесь и кроется “тайна Корана”: Аль Фуркан – Различение! Которую Аллах обещал дать тому, кто убоится гнева Его…. Я боялся этого на всем своем Пути, следуя в логике постижения истины правило: не приписывать великим строениям (чаше Соломона, Православному Кресту, Пирамиде Хуфу и др.) свои измышления. Но это разговор очень серьезный, потому продолжим в следующий раз. А пока…

Физические значения пирамиды Хуфу

Но тут произошло вот что. Один из моих друзей попросил меня, а вернее убедил, что мне надо дать истинные размеры  пирамиды Хеопса-Хуфу здесь! Я сделаю это, но теоретически и вместе с тем физически это будет истина. Но ответ может показаться здесь парадоксальным потому, что мы забегаем вперед.

Чему равен радиус окружности, если площадь ее равна – 3?

Ответ:

 

Физическое значение ее равно:

И эту единицу получают через скипетр Тутанхамона, как говорил. ОНА и есть искомая ЕДИНИЦА, заложенная в фундаменте (в “нулевой цикл”) строительства пирамиды Хуфу!

Но чему она равна в метрах? Для получения ответа разделим полученное значение на “пи/3” и получим – ”1 Единица” в метрах:

Как оно связано с человеком? Ответ: если вы возведете это значение: 0,9331405 в квадрат, то получите точное физическое значение, равное половине роста Адама (и моего роста). Т.е. это будет расстояние “от Земли, до основания моего полового органа” и это значение равно 0,8075… метра. Если вы извлечете из этого значения “квадрат” – то опять получите значение – 0,93314…метра, как Единица — Основание пирамиды. А искомый рост Адама в метрах составляет отсюда: 1,7415… метра. 

И подводя предварительный итог, моя колонка (первая) в этой таблице измерения пирамиды Хуфу будет выглядеть так:

Тут еще не приведены значения углов, как и не поместилась гран пирамиды AI  (Рис.1), которая равна:

AI=221,867…. метров!

Соискатели тайны пирамиды такими “мелочами” не интересуются видимо. Но именно в этих указанных выше трех углах и этих “граней” пирамиды и заключается главная тайна пирамиды Хеопса – как знания. А то, что открылось при этом  – “размеры”, “единица” это всего лишь прелюдия к серьезней теме!

Потому, следующая часть публикации и будет посвящена Квадратуре круга! Именно потому древние и передали нам, как Завет, задачу: чему равна “квадратура круга” с тем, чтобы мы поняли Пирамиду Хуфу, как замысел и предание древних. Ее предназначение.

Потому основной разговор впереди… А вы други мои пока считайте, думайте, сравнивайте. В общем учитесь. Хотя 90% из моих посетителей тут, учиться абсолютно неспособны. К великому сожалению. Они предпочитают сами учить других… “чему ни-будь и, как ни-будь”.

P.S. Други мои, продолжение следует и главное впереди. Именно здесь, вот это примечание я сделаю ссылкой еще, на новую часть работы, как опубликую. И это продолжение — главное в «тайне пирамиды». Просто надо в начале пояснить нечто новое.

Re: Геометрические соотношения в пирамиде Хеопса

#2  Степан » 31 окт 2017, 21:31

В камере Царя присутствует также ещё два объекта как минимум, которые также могут быть проверены на золотое соотношение и причастность числа Пи или других констант. Это саркофаг и обстоятельства расположения устьев вентиляционных шахт в камере и сами размеры шахт — для камеры Царя и Царицы эти обстоятельства разные. Размеры внешние саркофага пирамиды Хеопса: длина — 223,6 см, ширина — 97,8 см, высота — 104,9 см, внутренние размеры: длина — 198,3 см, ширина — 68,1 см, глубина — 87,4 см. Проверим размеры на причастность к целочисленному кубиту: 2,236/0,524 = 4,267; 0,978/0,524 = 1,866; 1,049/0,524 = 2,001; 1,983/0,524 = 3,784; 0,681/0,524 = 1,3; 0,874/0,524 = 1,668. Как видно только внешняя высота укладывается в целое значение в кубитах. Если вспомнить в камере Царя наоборот размер высоты камеры не укладывался в целое значение в кубитах. Проверим размеры на кратное присутствие золотого числа — 1,618 в размерах саркофага в см: 223,6/1,618 = 138,195.., 97,8/1,618 = 60,445.., 104,9/1,618 = 64,833.., 198,3/1,618 = 122,558.., 68,1/1,618 = 42,089.., 87,4/1,618 = 54,017. Аналогичная проверка на присутствие квадрата золотого числа: 223,6/2,618 = 85,409.., 97,8/2,618 = 37,357.., 104,9/2,618 = 40,069.., 198,3/2,618 = 75,745.., 68,1/2,618 = 26,012.., 87,4/2,618 = 33,384. Как видно на прямую размеры саркофага не взяты кратно ни золотому числу ни его квадрату. На присутствие числа Пи: 223,6/3,14 = 71,210.., 97,8/3,14 = 31,146.., 104,9/3,14 = 33,407.., 198,3/3,14 = 63,152.., 68,1/3,14 = 21,967.., 87,4/3,14 = 27,834. В размерах саркофага пирамиды Хеопса число Пи кратно не присутствует. Проверим соотношение полупериметра основания саркофага к его высоте: (2,236 + 0,978)/1,049 = 3,214/1,049 = 3,063… . Была речь об интересных объёмах саркофага, проверим: внешний объём — 2,236*0,978*1,049 = 2,293… м куб. Внутренний: 1,983*0,681*0,874 = 1,18 м куб. Объём гранита в саркофаге: 2,293 — 1,18 = 1,113 м куб. Процентная доля объёма гранита в объёме саркофага: 1,113/2,293 = 0,485… . Почти равен объём гранита объёму воздуха в саркофаге: 1,18 — 1,113 = 0,067 м куб, это почти составляет 1,5 %, воздуха на 1,5 % больше. Проверим простые соотношения: длина/ширина = 2,236/0,978 = 2,286; длина/высота = 2,236/1,049 = 2,132; ширина/высота = 0,978/1,049 = 0,932; необходимо перебрать соотношения внешних и внутренних размеров, я не буду приводить все пробы расчёта, если что-то проявится — напишу.
По саркофагу интересен факт, что внешняя высота и только она укладывается в целое значение в кубитах — 1,049 м = 2 кубита. Подспудно ощутим какой-то ребус, поскольку в камере Царя только пол имеет целые размеры в кубитах — 10 х 20 кубитов.
В фильме «Откровение пирамид» в том числе упоминается ещё один интересный факт о том, что если из длины окружности описанной на основании пирамиды вычесть длину вписанной окружности можно получить в качестве ответа значение скорости света в вакууме. Проверим: длина описанной окружности — 2*Пи*1,4142*115,165 = 1022,8 м, длина вписанной окружности: 2*Пи*115,165 = 723,24 м, 1022,8 — 723,24 = 299,56 м. Похоже на значение скорости света в вакууме — 299,79 тыс км/с, расхождение: ((299,79 — 299,56)/299,79)*100% = 0,08 %. Вот ещё одна интересная константа имеющая отображение в размерах основания пирамиды Хеопса — 230,33 метра.

Ау в лесу им. Кирова.

АРХИТЕКТУРА И ГРАДОСТРОИТЕЛЬСТВО

УДК 72.031

РАДЗЮКЕВИЧ АНДРЕЙ ВЛАДИСЛАВОВИЧ, канд. архит., доцент, radz@rambler.ru

МАРЧЕНКО ЮРИЙ ГРИГОРЬЕВИЧ, докт. культурологии, профессор, teneshev@yandex.ru

Новосибирская государственная архитектурно-художественная академия,

630099, г. Новосибирск, Красный проспект, 38

К ВОПРОСУ О РАЗМЕРАХ И ПРОПОРЦИЯХ ПИРАМИДЫ ХЕОПСА

В работе проводится сопоставление наиболее распространенных гипотез, описывающих логику формообразования пирамиды Хеопса. Исследуется научное предположение, основанное на пропорции золотого сечения. Текст Геродота о том, что боковая грань пирамиды Хеопса равна квадрату высоты пирамиды, однозначно дает основание для утверждения, что пропорция золотого сечения присутствует в геометрии пирамиды. Однако наличие иррациональной золотой пропорции вызывает сомнения в контексте уровня развития математики Древнего Египта. В статье предлагается иная трактовка текста Геродота, основанная на использовании так называемых квадратных чисел. Предложена новая метрологическая интерпретация размеров пирамиды Хеопса, что дает возможность осуществить реконструкцию логики ее формообразования.

Ключевые слова: историческая метрология; пирамида Хеопса; пропорция золотого сечения; число Пи; квадратные числа.

ANDREI V. RADZYUKEVICH, PhD, A/Professor, radz@rambler.ru

YURIIG. MARCHENKO, DSc, Professor, teneshev@yandex.ru

Novosibirsk State Academy of Architecture and Fine Arts, 38, Krasnyi Ave., 630099, Novosibirsk, Russia

PYRAMID OF CHEOPS: SIZES AND PROPORTIONS

The paper presents a comparison of the most widespread hypotheses describing the principles of formation of the Pyramid of Cheops. A scientific guess based on a golden ratio is investigated in this paper. Herodotus’s text about the fact that the lateral side of the Pyramid is equal to its height square, unambiguously proves the statement that the golden ratio is present in the Pyramid geometry. However, the existence of irrational golden ratio proportion raises

© Радзюкевич А.В., Марченко Ю.Г., 2015

doubts in relation to the level of development of mathematics in Ancient Egypt. The paper gives the different interpretation of Herodotus’s text based on the use of the perfect square. Also, a new metrological interpretation of the Pyramid dimensions is suggested that gives the possibility of modifying its formation principles.

Keywords: historical metrology; Pyramid of Cheops; golden ratio; the number n; perfect square.

Пирамида Хеопса (Khufu) совместно с комплексом пирамид в Гизе относится к числу ключевых памятников истории мировой архитектуры (рис. 1).

Рис. 1. Пирамида Хеопса в составе комплекса пирамид в Гизе

Изучению геометрии пирамиды посвящено огромное количество исследований, в которых содержится целый ряд гипотез с реконструкцией логики формообразования пирамиды. В большом количестве научных и научно-популярных текстов приводятся различные доводы о наличии в пирамиде Хеопса пропорции золотого сечения. Главным основанием для «золотой» гипотезы служит утверждение Геродота о том, что площадь боковой грани пирамиды равна квадрату ее высоты. Подобное сообщение о математической особенности геометрии пирамиды, по всей видимости, является уникальным и, очевидно, не случайным. Следует уточнить смысл текста Геродота. В русском переводе Г.А. Стратановского текста о пирамиде Хеопса (книга II, часть 124) говорится, что «она четырехсторонняя, каждая сторона ее шириной в 8 плефров и такой же высоты» [1]. Неточность перевода была отмечена Д.Д. Мордухай-Болтовским [2] и А.И. Щетниковым [3]. Они предлагают иную формулировку: «У неё с каждой стороны грань в восемь плефров, равная квадрату высоты», т. е. каждая грань пирамиды имеет площадь, равную квадрату высоты пирамиды (рис. 2).

Рис. 2. Геометрическая схема пирамиды Хеопса, соответствующая формуле Геродота (площадь боковой грани пирамиды равна квадрату ее высоты)

Рассмотрим детально вопрос о соотношении площади грани пирамиды к ее высоте. Обозначим высоту пирамиды, половину стороны основания и медиану как А, В и С соответственно (рис. 3).

Рис. 3. Геометрическая схема пирамиды Хеопса с обозначением высоты пирамиды (а), медианы (с) и половины стороны основания (в)

Площадь боковой грани пирамиды равна ВхС. В соответствии с теоремой Пифагора получается, что

А2 + В2 = С2.

Кроме того, исходя из текста Геродота получается, что

ВхС = А2.

Следовательно, подставляя ВхС вместо А2, получаем

ВхС + В2 = С2.

Решая это уравнение, ориентируясь на современный уровень развития математики, получаем, что длина медианы пирамиды должна относиться к половине ее основания в пропорции, которую принято называть пропорцией золотого сечения и обозначать буквой «Ф» (рис. 4).

Рис. 4. Наличие пропорции золотого сечения в пирамиде Хеопса в соответствии с формулировкой Геродота

Более того, формулировка Геродота содержит в себе еще одну любопытную закономерность, отмеченную Д.Д. Мордухай-Болтовским, — медиана пирамиды так относится к ее высоте, как высота относится к половине основания. Иначе говоря, гипотенуза треугольника так относится к большому катету, как большой катет относится к малому катету. Очевидно, что это условие выполняется только в случае отношения гипотенузы к малому катету в пропорции золотого сечения.

Не затрагивая пока вопроса об историчности такого подхода, посмотрим, как соотносится с формулой Геродота еще одна широко распространенная гипотеза, согласно которой в форме пирамиды присутствует целочисленная пропорция 14/11. Предполагается, что она символизирует «круговые» соотношения, связанные с дробью 22/7, которая в древности могла использоваться в качестве целочисленного аналога числа Пи.

Предположим, что соотношение 14/11 справедливо как для отношения гипотенузы к большому катету, так и для отношения большого катета к малому. Анализ проведенных ранее исследований показывает, что такое двойное использование пропорции 14/11, судя по доступной нам литературе, пока не применялось. Допуская это предположение, получаем, что связать размеры малого катета, большого катета и гипотенузы можно через целочисленную цепочку модулей 121 — 154 — 196 (рис. 5).

В данном случае отношение медианы к половине стороны получается равным 1,6198347 (196/121), что отличается от золотого соотношения всего лишь на 0,11 % или на 1/900 часть.

В связи с этим произведем детальное сопоставление представленных гипотез: «иррационально-золотой» и «целочисленно-круговой». Обратимся прежде всего к фактическим обмерам пирамиды Хеопса. Общепринятыми в настоящее время считаются следующие размеры этого древнейшего сооружения: длина основания равна 230,37 м, а вычисленная из угла наклона граней пирамиды высота — 146,6 м [4]. Расчетный размер апофемы при этом состав-

ляет 186,44 м. Фактическое отношение высоты пирамиды к половине ее основания равно 1,272735. Если следовать «золотой» гипотезе, то этот коэффициент представляет собой л/ф и равен 1,27201965. Если же придерживаться гипотезы, основанной на дроби 14/11, то этот коэффициент получается равным 1,272727272. Сопоставляя полученные коэффициенты, следует отметить, что второй вариант точнее «золотого» более чем в 90 раз. Если же сопоставить оба этих коэффициента с фактическими реальными размерами, то, полагая длину основания пирамиды базовой величиной, получаем, что высота пирамиды в первом случае должна быть равна 146,599 м, а во втором — 146,518 м. Отмечая просто невероятное идеально-фантастическое соответствие (1 мм погрешности) первого варианта фактическому значению, заметим также, что и «золотой» вариант исключительно точен. Отклонение составляет всего 82 мм на 146,6 м.

14/ 11

I

Рис. 5. Пропорциональные целочисленно-модульные соотношения между основными элементами пирамиды Хеопса

Рассмотрим историко-метрологические особенности пирамиды Хеопса. Исходя из приведенных вычислений и фактических размеров сторон основания и высоты пирамиды, получаем величину модуля, равную 0,952 м. Размер в 196 таких модулей равен 186,59 м, что отличается от расчетного размера апофемы (186,44 м) на 15 см. Учитывая, что погрешность колебаний фактических размеров в сторонах основания пирамиды составила 20,1 см, можно констатировать, что погрешность в 15 см не превышает

фактические колебания размеров и ею можно пренебречь. Гипотеза золотого сечения, основанная на иррациональном значении «золота», дает размер апофемы в 186,37 м, что меньше размера, рассчитанного по теореме Пифагора, на 7 см. Если же ориентироваться на исторически более оправданную «целочисленно-золотую» гипотезу, представленную в работе Ли-вио Стеччини [5], согласно которой формообразующий треугольник пирамиды Хеопса содержит стороны, соотносящиеся как 55х70х89, погрешность получается равной 5 см. Следовательно, обе гипотезы по соответствию фактическим размерам следует признать истинными. Теперь рассмотрим обе гипотезы на предмет их соответствия данным по исторической метрологии. Вариант Стеччини отвечает общепринятому положению о том, что высота пирамиды Хеопса и сторона ее основания равны соответственно 280 и 440 локтям царским. И в этом случае расчетная величина апофемы получается равной 356 таким локтям (89х4). Однако использование величины царского локтя в пирамиде Хефрена (КЪай»а) дает такие «неудобные» величины, как 410 и 273 ед. [4]. Хотя практически все исследователи безоговорочно признают, что формообразующим треугольником для этой пирамиды был простейший египетский треугольник со сторонами 3х4х5. В данном случае катеты, равные 205 и 273 царским локтям, не соответствуют соотношению 3/4, и поэтому данный метрологический подход содержит внутреннее противоречие.

Рассмотрим подробнее полученный модуль (0,952 м). В первом приближении эту величину можно интерпретировать как два локтя по 0,476 м или три фута по 0,317 м. По исследованиям Н.Н. Болотина, подобные размеры локтя и фута составляли основу так называемой древнеассирийской системы мер [6]. По его мнению, она образовалась в результате уменьшения мер так называемой среднемесопотамской системы на 1/10 величину. Так, локоть среднемесопотамский обыкновенный, равный 0,528 м, был уменьшен до 0,475 м. Соответственно, фут в 0,352 м сократился до 0,3168 м. Исследование Н.Н. Болотина показывает, что подобные приемы с уменьшением мер на 1/10 величины встречались в истории древних мер неоднократно. Например, фараон Эхнатон (Аменхотеп IV) провел аналогичную налоговую реформу, уменьшив налоги с населения на 1/10 часть. Следовательно, предположим, что полученный нами модуль равен двум локтям, каждый из которых имеет размер в 9/10 от египетского царского локтя. В этом случае используемые нами меры будут соотноситься между собой следующим образом:

локоть царский/10 = локоть расчетный/9 = фут расчетный/6.

Данная метрологическая реконструкция имеет целый ряд косвенных подтверждений. Во-первых, следует отметить, что единственная находка археологов и, очевидно, самый главный элемент пирамиды Хеопса — сохранившийся в камере фараона саркофаг (рис. 6) снаружи имеет ширину 0,96 м и длину 2,24 м, что достаточно точно можно интерпретировать как 3 и 7 расчетных фута.

Рис. 6. Фото сохранившегося гранитного саркофага из пирамиды Хеопса

Учитывая, что толщина стенок равна 0,16 м, внутренние размеры саркофага получаются равными 2 и 6 расчетным футам. Наружная ширина саркофага фактически равна принятому нами модулю соразмерения параметров пирамиды Хеопса. Во-вторых, по подсчетам Ф. Петри, пирамида Хеопса содержит около 2 300 000 блоков весом 2,5 т каждый, размером в среднем 127x127x71 см [7]. В переводе на реконструируемые меры получаем цепочку в 4x4x2,25 фута по 0,317 м. В переводе на ладони (1/4 фута) получаем цепочку в 16x16x9 ладоней. Характерно, что числа 16 и 9 являются квадратными числами.

Необходимо также отметить, что размер в 1,27 м есть величина, тождественная двойному шагу, упоминаемому у Витрувия. Он пишет, что Эрато-сфен вычислил длину окружности Земли равной 252 000 стадиям (700 стадий на один градус), что равно также 31 500 000 шагам [8]. Учитывая, что по оценкам метрологов Эратосфен очень точно измерил длину окружности Земли, получаем, что величина шага равна примерно 1,27 м (вероятно, имелся в виду размер двойного шага), т. е. она идентична 4 расчетным футам. Поскольку в стадии получается 125 таких шагов (31500000/252000), то в ней, соответственно 500 таких футов. Длина стадии Эратосфена в этом случае становится равной примерно 158,7 м. Следует отметить, что в этой стадии содержалось также 300 «местных локтей» [9]. Отсюда получается, что «местный локоть» был равен 0,529 м, а его величина соотносилась с футом в пропорции 5/3 или 10/6, что соответствует принятой выше метрологической модели. Заметим, что числа 10 и 6 имели в древней нумерологии особый статус. Об этом имеется упоминание в трактате Витрувия «Десять книг об архитектуре». В книге третьей он сообщает, что древние зодчие «…за основание мер, явно необходимых при всяких работах… установили число десять». Однако, «математики, возражая на это, считают совершенным числом шесть». И только позднее, «когда усмотрели, что оба числа, и шесть и десять, совершенны, то соединили их в одно и получили совершеннейшее число — шестнадцать».

По мнению известного египтолога Жана-Филиппа Лауэра [10], в пирамиде Хеопса целочисленной дробью определяется не только угол наклона апофемы, но и угол наклона ребра. Он считает, что высота пирамиды соотносится с половиной длины диагонали основания в пропорции 9/10. В этом случае можно допустить, что зодчий пирамиды мог одновременно использовать как царский локоть, так и расчетный локоть в 0,475 м, определяя высоту пирамиды в 308 локтей расчетных, а полудиагональ основания — в 308 локтей царских. Очень хорошо косвенно подтверждает принятую гипотезу метрологическая интерпретация размеров рядом стоящей пирамиды Хефрена. Ее высота получается равной «круглому» числу в 300 расчетных локтей. Сторона основания при этом равна 450 локтям. В этом случае соотношение половины длины основания к высоте оказывается тождественным соотношению катетов в египетском треугольнике 300/225 = 4/3. Соответственно, апофема получается равной 375 таким локтям.

Для сопоставления гипотез можно также обратиться к размерам третьей пирамиды комплекса в Гизе — пирамиды Микерина (Мепкаига). Однако данные по ее обмерам настолько противоречивы, что делать это можно только с большой долей условности. В работе [10] сообщается, что наклон ее граней тождествен наклону граней пирамиды Хеопса — примерно 52°. Длина основания и высота пирамиды принимаются равными соответственно 202 и 125 локтям царским, что почему-то трактуется как соотношение, близкое 22/14. Приведенные в Википедии примерные обмерные данные (102,2-104,6 м — стороны основания и 65,55 м — высота) дают возможность предположить, что эти размеры соответствуют 220 и 140 расчетным локтям по 0,475 м. Нетрудно заметить, что получилось соотношение, тождественное соотношению размеров пирамиды Хеопса — 220/140 = 484/308. Исходя из этих размеров получается, что пирамиды Хеопса и Микерина находятся в пропорции 11/5. Представим все реконструкции проектных размеров пирамид на рис. 7.

Рис. 7. Реконструкция проектных размеров пирамид в Гизе (мера — расчетный локоть

Конечно, сложно говорить о какой-либо реконструкции логики формообразования ансамбля пирамид. Даже предположение о том, что все они были сделаны в соответствии с неким единым замыслом, кажется весьма смелым.

Пирамида Хефре-

0,475 м)

Тем не менее используемая мера длины вполне целочисленно и «кругло» описывает все основные размеры пирамид комплекса. Такая реконструкция проектных размеров может стать основой для дальнейших поисков логики формообразования. Вполне возможно, что полученные числовые значения можно будет рассматривать в аспекте архитектурной космологии и символики [11].

Рассмотрим ниже обозначенные гипотезы в аспекте их соответствия истории математики. Вопрос о сознательном использовании пропорции золотого сечения в пирамиде Хеопса является очень спорным. Золотая пропорция является величиной иррациональной, а древние египтяне, судя по историческим документам, могли оперировать только целыми числами и дробями. Впервые в исторических текстах эта пропорция была зафиксирована только в III в. до н. э. в «Началах» Эвклида при решении задачи геометрического построения правильного пятиугольника и пятнадцатиугольника.

В исследованиях ряда авторов высказывается предположение о том, что пропорция золотого сечения первоначально была зафиксирована в текстах Платона (перевод С.С. Аверинцева). В диалоге «Тимей» приводится следующая формула пропорциональной взаимосвязи: «Прекраснейшая же из связей такая, которая в наибольшей степени единит себя и связу-емое, и задачу эту наилучшим образом выполняет пропорция, ибо, когда из трех чисел — как кубических, так и квадратных — при любом среднем числе первое так относится к среднему, как среднее к последнему, и соответственно последнее к среднему, как среднее к первому, тогда при перемещении средних чисел на первое и последнее место, а последнего и первого, напротив, на средние места выяснится, что отношение необходимо остается прежним, а коль скоро это так, значит, все эти числа образуют между собой единство». Однако детальный разбор текста Платона, проведенный В.С. Беляниным, показывает, что пропорция золотого сечения тут ни при чем [12]. При условии, что исходные числа являются либо квадратными, либо кубическими, всегда можно вычислить «среднее» значение, удовлетворяющее формуле Платона. При этом пропорциональные соотношения между выбранными числами могут быть самыми разными. Например, если взять два произвольных квадратных числа, допустим 9 (3×3) и 25 (5×5), то можно вычислить что «наилучшим связующим» между ними будет число 15. Пропорциональные соотношения 25/15 и 15/9 оказываются равными 1,666666. А для квадратных чисел, допустим 9 (3×3) и 36 (6×6), «связующим» числом будет 18. И пропорция между 36/18 и 18/9 будет равна 2. Фактически для любой пары квадратных или кубических чисел можно найти «наилучшее общее связуемое» (табл. 1).

Для нашего же конкретного случая чрезвычайно важным следует считать то обстоятельство, что речь в этом высказывании идет именно о квадратных и кубических числах. В нашей гипотезе апофема и половина длины основания (гипотенуза и малый катет) описываются с помощью именно квадратных чисел — 11×11 и 14×14. Большой катет (высота пирамиды) в этом случае и является «наилучшим связуемым», т. к. он является средним геометрическим между малым катетом и гипотенузой: 11×14 = 154.

Таблица 1

Вычисление средних значений для двух произвольных квадратных чисел

(от 4 до 256)

2×2 3×3 4×4 «5×5 6×6 7×7 8×6 «9×9 10×10 «[11×11 12×12 «13×13 14×14 15×15 16×16

4 ¡9 16 25 ¡36 49 64 81 100 121 144 160 196 225 256

16×1 в 256 32 :4в 64 50 96 112 12В 144 160 176″ 192 208″ 224 240 (

15×15 225 30 45 60 75 90 105 120 135 150 165 160 195 210

14×14 196 28 [42 56 70 84 98 112 126 140 154 168 182

13×13 169 26 39 52 65 78 91 104 117 130 143 156

12×12 144 24 36 [Во 72 64 96 108 120 132

11*11 121 22 33 44 55 66 77 88 99 110

10×10 100 20 эо «40 50 60 70 80 90

5×9 81 13 [27 36 45 54 63 72

8×8 64 16 Й4 32 40 48 56

7×7 ад 14 21 «[28 ;35» 42 196-154-121 Пирамида Хеопса

:вхБ 36 12 Г® 24 30

:5х5 25 10 15 20 81-36-16 Па рфено в Афинах

■4*4 1ё в П2

¡3×3 9 6

:2*2 4

Особенность данного случая состоит в том, что зодчему нужно было подобрать среднее не для любых произвольных квадратных или кубических чисел, а для тех чисел, которые бы позволили построить прямоугольный треугольник. В этом случае величина большего числа (гипотенузы) должна соотноситься с величиной меньшего числа (малого катета) в пропорции, близкой к той, которую сегодня принято называть золотым сечением. Поэтому формулировку Платона можно связать с пропорцией золотого сечения только в одном случае, когда все три числа образуют стороны прямоугольного треугольника. При этом соотношение катетов теоретически должно быть равно примерно значению 1,272.

Рассмотрим, велика ли вероятность появления таких вариантов, одновременно соответствующих и формуле Платона, и теореме Пифагора. Для предварительной проверки возьмем только первые 25 квадратных чисел (табл. 2).

Как видно из приведенных примеров, вариант, тождественный пропорциям пирамиды Хеопса, является наиболее точным — всего 0,114 %. Если предположить, что зодчий использовал именно такой подход при определении размеров, то становится понятным, что решающее влияние на выбор варианта оказала его исключительно высокая точность соответствия формуле, тождественной теореме Пифагора. Как именно производился подбор числовых значений, можно только предполагать. Очевидно, что современный подход к решению данной задачи, базирующийся на решении биквадратного уравнения, не мог быть использован в то время. Иначе придется признать достоверной гипотезу о неких космических пришельцах. По всей видимости, расчет проводился на основе эмпирического подбора трех чисел, соответствующих исходным условиям «совершенства». Можно предположить, что поиск нужного варианта происходил с помощью раскладывания на плоскости фигурных квадратных и прямоугольных чисел и с использованием схем гномона.

Следует также отметить, что использование пропорций, тождественных формулировке Платона, по всей видимости, было предпринято в Парфеноне. Соотношение длины стилобата, ширины стилобата и высоты ордера, вероят-

но, определялось зодчими по целочисленной цепочке 81 — 36 — 16 [13]. Отличие заключалось в том, что зодчим не нужно было выстраивать из этих величин прямоугольный треугольник.

Таблица 2

Вычисление пропорций целочисленных прямоугольных треугольников

Число Гипотенуза Большой Малый Приближенно- целочисленная Погрешность,

(число катет катет цепочка %

в квадрате)

2 4 3.1447 2 472

3 9 7.0755 5.562

4 10 12,579 9.889

5 25 19,054 15,451

6 36 28,302 22,250

7 49 36.522 30,285

0 64 50,314 39,555

9 81 63,078 50,062 81-63-49 9×9 — 9×7 — 7×7 2,167%

10 100 78,610 61,805

11 121 95,126 74,784

12 144 113,208 88.999

13 109 132,862 104,451

14 190 154,088 121,138 190-154-121 14×14-14×11 -11×11 0,114%

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

15 225 176,837 139,062

10 250 201,258 158,222

17 289 227,201 178,017

18 324 254,717 200,249

19 301 283,805 223,117 361-285-225 19×19-19×15 -15×15 0,837%

20 400 314,465 247,221

21 441 346,698 272,501

22 484 380,503 299,138

23 529 415,881 326,950 529-414-324 23×23 — 23×18 — 18×16 0,910%

24 576 452,830 355,998

25 625 491,352 336,233

Что же касается гипотезы золотого сечения, то для использования ее при анализе форм древнеегипетских памятников нет исторических оснований. В фундаментальной работе Roger Herz-Fischler [14], посвященной изучению исторических документов, содержащих прямые или косвенные сведения о золотом сечении, показывается, что к периоду Древнего Египта можно отнести только рисунки пентаграммы. Указывается также, что вавилоняне умели на основе модульных соотношений строить фигуру пентаграммы на основе прямоугольного треугольника 3-4-5 (рис. 8).

60 30

Рис. 8. Способ целочисленного построения фигуры пентаграммы (Древний Вавилон)

Любопытно, что абсолютно такой же способ построения правильного пятиугольника приводит теоретик архитектуры эпохи Возрождения Винченцо Скамоцци в своем трактате по архитектуре [15]. На 32-й странице трактата представлены приближенно целочисленные схемы правильных многоугольников (рис. 9).

ОеПАгсЬгсе». & Утс:5сашвгг?,

Рис. 9. Страница из трактата Винченцо Скамоцци (1615 г.)

На одной из схем (выделено красным) приведена схема правильного пятиугольника, построенного с помощью десяти треугольников со сторонами 3x4x5, известного в истории математики как египетский треугольник (рис. 10).

Рис. 10. Схема приближенного построения правильного пятиугольника (В. Скамоцци)

Рассмотренный материал дает возможность предположить, что присутствие в пирамиде Хеопса «золотой» пропорции носит случайный характер как побочный результат поиска пропорций «особого» прямоугольного треугольника, в котором гипотенуза относится к большому катету так же, как большой катет относится к малому катету.

Попытки интерпретировать пропорции пирамиды Хеопса с помощью гипотезы золотого сечения следует признать недостаточно убедительными, т. к. они имеют весьма слабые историко-математические обоснования в сравнении с целочисленно-модульными интерпретациями. Представленная гипотеза хорошо соотносится с работами [16, 17], в которых собрана определенная аргументация против использования пропорции золотого сечения в искусствоведческих исследованиях.

Библиографический список

1. Геродот. История : в 9 кн. / пер. и примеч. Г.А. Стратановского. — Л. : Наука, 1972. -600 с.

2. Начала Эвклида : в 3 т. / пер. и комм. Д.Д. Мордухай-Болтовского при ред. участии И.Н. Веселовского и М.Я. Выгодского. — М. : ГТТИ, 1949. — 50 с.

3. Щетников, А.И. Золотое сечение, квадратные корни и пропорции пирамид в Гизе / А.И. Щетников. — Условия доступа : http://www.nsu.ru/classics/pythagoras/Pyramis.pdf

4. Силиотти, А. Египет. Пирамиды (Атлас чудес света) / А. Силиотти. — М., 1999. — 166 с.

5. Livio Catullo Stecchini. A History of Measures. The Dimensions of the Great Pyramid. -Условия доступа : http://www.metrum.org/measures/dimensions.htm

6. Болотин, Н.И. Формирование и развитие мер, их назначение для исследования памятников материальной культуры: дис. … докт. архит. — Новосибирск, 1975. — 354 с.

7. Непомнящий, Н.Н. По следам великанов / Н.Н. Непомнящий. — М. : Олимп; ООО «Фирма Издательство ACT», 1998. — 512 с.

8. Витрувий. Десять книг об архитектуре / Витрувий ; пер. с латинского Ф.А. Петровского. Изд. 2-е, испр. — М., 2003. — 205 с.

9. Томпсон, Дж.. История древней географии / Дж. Томпсон. — М. : Изд-во иностранной литературы, 1953. — 590 с.

10. Corinna, Rossi. Arch^^re and mathematks in Antient Egypet / R. Corinna // Cambridge university press. — 2003. — 280 p.

11. Поляков, Е.Н. Образ вселенной в культовом зодчестве древнего мира / Е.Н. Поляков. -Томск : Изд-во ТГАСУ, 2009. — 434 с.

12. Белянин, В.С. Владел ли Платон кодом золотой пропорции? Анализ мифа. — Условия доступа : http://www.a3d.ru/archi/stat/no_mif.php

13. Радзюкевич, А.В. Золотой блеск модулей Парфенона / А.В. Радзюкевич // Архитектура, приложение к Строительной газете. — 1989. — № 14. — 195 с.

14. Herz-Fischler, Roger. A mathematical history of the golden number / Roger Herz-Fischler. -Mineola, NY, 1998. — 180 p.

15. Scamozzi, V. Architettura universal / V. Scamozzi. — Venezia. — 1694. — 287 p.

16. Радзюкевич, А.В. Критический анализ исследования Адольфа Цейзинга — основоположника гипотезы «золотого сечения» / А.В. Радзюкевич // AMIT 4(29) 2014. — Условия доступа : http://marhi.ru/AMIT/2014/4kvart14/radzukevich/radzukevich.pdf

17. Радзюкевич, А.В. К вопросу о научном изучении пропорций в архитектуре и искусстве / А.В. Радзюкевич // Ползуновский вестник. — 2014. — № 1. — С. 159-164. — Условия доступа : http://elib.altstu.ru/elib/books/Files/pv2014_01/pdf/159radzukevich.pdf

References

1. Stratanovskii G.A. Gerodot. Istoriya [Herodotus, History]. In 9 books. Leningrad : Nauka Publ., 1972. 600 p. (transl. from Gr.)

2. Mordukhai-Boltovskii D.D. Nachala Evklida [Euclid’s Elements]. In 3 vol. Moscow : GTTI Publ., 1949. 50 p. (transl. from Gr.)

3. Shchetnikov A.I. Zolotoe sechenie, kvadratnye korni i proportsii piramid v Gize [Golden ratio, square roots and proportions of pyramids in Giza]. Available at : http://www.nsu.ru/classics/pythagoras/Pyramis.pdf (rus)

4. Siliotti A. Egipet. Piramidy (Atlas chudes sveta) [Guide to the Pyramids of Egypt]. Moscow. 1999. 166 p. (transl. from It.)

5. Stecchini L.C. A History of Measures. The Dimensions of the Great Pyramid. Available at : http://www. metrum. org/measures/dimensions.htm

6. Bolotin N.I. Formirovanie i razvitie mer, ikh naznachenie dlya issledovaniya pamyatnikov ma-terial’noi kul’tury [Formation and development of measures, their purpose in study of cultural heritage. PhD thesis]. Novosibirsk. 1975. 354 p. (rus)

7. Nepomnyashchii N.N. Po sledam velikanov [In the footsteps of giants]. Moscow : AST Publ., 1998. 512 p. (rus)

8. VitruviusM. Desyat’ knig ob arkhitekture [Ten Books on Architecture]. Moscow : 2003. 205 p. (transl. from Lat.)

9. Thomson J.O. Istoriya drevnei geografii [History of Ancient Geography]. Moscow : 1953. 590 p. (transl. from Engl.)

10. CorinnaR. Architecture and mathematics in Ancient Egypt. Cambridge university press. 2003. 280 p.

11. Polyakov E.N. Obraz vselennoi v kul’tovom zodchestve drevnego mira [Image of the Universe in cult architecture of the ancient world]. TSUAB Publ., 2009. 434 p. (rus)

12. Belyanin V.S. Vladel li Platon kodom zolotoi proportsii? Analiz mifa [Had Plato the code of the golden ratio? Analysis of the myth]. Available at : http://www.a3d.ru/archi/stat/no_mif.php (rus)

13. Radzyukevich A.V. Zolotoi blesk modulei Parfenona [Gold gloss of Parthenon’s modules]. Arkhitektura, prilozhenie k Stroitel’noi gazete. 1989. No. 14. 195 p. (rus)

14. Herz-Fischler R. A mathematical history of the golden number. Mineola, NY, 1998. 180 p.

15. Scamozzi V. Architettura universale. Venezia. 1694. 287 p.

16. Radzyukevich A.V. Kriticheskii analiz issledovaniya Adol’fa Tseizinga — osnovopolozhnika gipotezy ‘zolotogo secheniya’ [The critical analysis of research by Adolf Zeising — the founder of golden ratio hypothesis]. AMIT 4. 2014. Available at : http://marhi.ru/AMIT/2014/4kvart14/radzukevich/radzukevich.pdf (rus)

17. Radzyukevich A.V. K voprosu o nauchnom izuchenii proportsii v arkhitekture i iskusstve [Scientific study of proportions in architecture and art]. Polzunovskii Vestnik. No. 1. 2014. Pp. 159-164. Available at :

http://elib.altstu.ru/elib/books/Files/pv2014_01/pdf/159radzukevich.pdf (rus)

Введение

Пирамида Хеопса
Египетское название <hiero>Aa1-G43-I9-G43</hiero> <hiero>G25-N18:X1-O24</hiero> Achet-Chufu 3ḫt ḫwfw «Горизонт Хуфу» Данные Месторасположение Гиза Заказчик ? Время строительства IV династия (~2560 до ~2540  до н. э.) Тип Пирамида Строительный материал Известняк Размер основания 230 м Высота (первоначально) 146,60 м Высота (сегодня) 138,75 м Наклон 51° 50′ Культовая пирамида нет

Координаты: 29°58′45″ с. ш. 31°08′03″ в. д. / 29.97917° с. ш. 31.13417° в. д. ^(G) (O)

Пирами́да Хео́пс (Хуфу) — крупнейшая из египетских пирамид, единственное из «Семи чудес света», сохранившееся до наших дней. Строительство, продолжавшееся двадцать лет, началось около 2560

года до н. э. Известны десятк и египетских пирамид. На плато Гиза самые крупные из них — пирамиды Хеопса, Хефрена и Микерина. Архитектором Великой пирамиды считается Хемиун, визирь и племянник Хеопса. Он также носил титул «Управляющий всеми стройками фараона». Более трёх тысяч лет (до постройки кафедрального собора в Линкольне, Англия, около 1300 года) пирамида являлась самой высокой постройкой на Земле.

Данные пирамиды Хеопса

• Высота (начальная): 146,60 м (по подсчетам) или 280 Королевских локтей (1 Королевский локоть = 52,920 см)
• Высота (сегодня): ≈ 138,75 м
• Угол: 51° 50′
• Длина боковой грани (изначально): 230,33 м (по подсчетам) или около 440 Королевских локтей
• Длина боковой грани (сейчас): около 225 м
• Длина сторон основания пирамиды: юг — 230,454 м; север — 230,253 м; запад — 230,357 м; восток — 230,394 м.
• Площадь основания (изначально): ≈ 53 000 м² (5,3 га)
• Площадь пирамиды: (изначально) ≈ 85 500 m²
• Периметр: 922 м.
• Общий объем пирамиды без вычета полостей внутри пирамиды (изначально): ≈ 2,58 млн м³
• Общий объем пирамиды, после вычета всех известных полостей (изначально): 2,50 млн м³
• Средний размер наблюдаемых каменные блоков: 1,0 м в ширину, высоту и глубину (но большинство имеет прямоугольную форму.)
• Средняя масса каменных блоков: 2,5 т
• Самый тяжелый каменный блок: 15 т
• Количество блоков: около 2,5 млн.
• По подсчетам общий вес пирамиды: около 6,25 млн т

Точно определить первоначальные параметры пирамиды не представляется возможным, поскольку её края и поверхности в настоящее время большей частью разобраны и уничтожены. Это затрудняет вычисление точного угла наклона. Кроме того, ее симметрия сама по себе не является идеальной, так что при разных измерениях наблюдаются отклонения в цифрах. В литературе по египтологии к одинаковым результатам в измерениях пришли Peter Jánosi, Mark Lehner, Miroslav Verner, Zahi Hawass и Alberto Siliotti. Они считали, что длина сторон может быть от 230,33 до 230,37 м. Зная длину стороны и угол при основании они вычислили высоту пирамиды — с 146,59 до 146, 60 м. Наклон пирамиды составляет 51° 50′, что соответствует секеду в 5 1/2 пальм, древнеегипетской единице измерения наклона, которая определяется как отношение половины основания к высоте. С учётом того, что в одном локте (кубите) 7 пальм, получается, что при таком выбранном секеде отношение основания к высоте равняется 22/7, хорошо известное с древности приближение числа Пи. Которое, судя по всему, получилось случайно, так как у других пирамид были выбраны другие значения для секеда.^[1]

Основание пирамиды покоится на природном скальном возвышении высотой в центре около 9 м.

О пирамиде

Пирамида называется «Achete-Chufu» — «Возрождение Хуфу (Хеопса)». Состоит из блоков известняка, базальта и гранита. Она была построена на естественном холме. Несмотря на то, что пирамида Хеопса, самая высокая и самая лучшая из всех египетских пирамид, но все же фараон Снофру построил пирамиды в Мейдуме и в Дахшуте (Ломаная пирамида и Розовая пирамида), общая масса которых оценивается в 8,4 млн тонн. Это значит, что для постройки этих пирамид было использовано на 2.15 млн.т. или на 25,6 % больше материала, чем это потребовалось на пирамиду Хеопса.

Первоначально пирамида была облицована более твердым, чем основные блоки, белым песчаником. Верх пирамиды венчал позолоченный камень — пирамидион. Облицовка сияла на Солнце персиковым цветом, словно «сияющее чудо, которому сам бог Солнца Ра, казалось, отдал все свои лучи». В 1168 г. н. э. арабы разграбили и сожгли Каир. Жители Каира сняли облицовку с пирамиды, для того чтобы построить новые дома.

Есть версия, которая достаточно хорошо объясняет, как была построена пирамида и точность подгонки отдельных блоков. Это версия состоит в том что пирамида построена из бетонных блоков, созданных фактически путем постепенного поднятия опалубки и изготовления блоков сразу на местах — отсюда и такая точность подгонки. В работах некоторых исследователей как, например, сэра Уильяма Флиндерса Петри «Пирамиды и Храмы Гизы», и в работе Кристофера Данна «Загадка древних египетских машин», а также подтверждёнными фото- и видеосъемками во время экспедиции под руководством Андрея Склярова, после внимательного исследования идеально сохранившихся блоков наружной отделки и внутреннего пространства пирамид были найдены следы, которые были интерпретированы ими как машинная обработка камня, что заставило этих исследователей поставить под вопрос авторство и время строительства пирамид.^[2][3] В то же время большинство учёных признают такой подход неакадемическим.

Структура пирамиды

Вход в пирамиду находится на высоте 15.63 метров на северной стороне. Вход образуют каменные плиты, уложенные в виде арки. Этот вход в пирамиду был заделан гранитной пробкой. Описание этой пробки можно найти у Страбона. Сегодня туристы попадают внутрь пирамиды через 17 м пролом, который сделал в 820 г. халиф Абу Джафар аль-Ма’мун. Он надеялся найти там несметные сокровища фараона, но обнаружил там только слой пыли толщиной в пол-локтя.

Внутри пирамиды Хеопса находятся три погребальные камеры, расположенные одна над другой.

Погребальная «яма»

Нисходящий коридор длиной в 105 м, идущий под наклоном 26° 26’46, приводит к горизонтальному коридору длиной 8,90 м, ведущему к камере 5. Расположенная ниже уровня земли, в скальном известняковом основании, она осталась незавершенной. Размеры камеры 14×8,1 м, она вытянута с востока на запад. Высота достигает 3,5 м. У южной стены камеры имеется колодец глубиной около 3 м, от которого в южном направлении на 16 м тянется узкий лаз (0,7×0,7 м в сечении), заканчивающийся тупиком. Инженеры John Shae Perring и Howard Vyse в начале XIX в. в камере разобрали пол и вырыли глубокий колодец глубиной 11,60 метров, в котором они надеялись обнаружить скрытую погребальную комнату. Они основывались на свидетельствах Геродота, утверждавшего, что тело Хеопса находится на острове, окруженном каналом в скрытой подземной камере. Их раскопки ни к чему не привели. Поздние исследования показали, что камера была брошена незавершенной, а погребальные камеры было решено устроить в центре самой пирамиды.

Несколько фотографий, сделанных в 1910 году

Восходящий коридор и Палаты царицы

От первой трети нисходящего прохода (через 18 м от главного входа) вверх под тем же углом 26,5° идёт на юг восходящий проход (6) длиной около 40 м, оканчивающийся в нижней части Большой галереи (9).

В своём начале, восходящий проход содержит 3 большие кубические гранитные каменные «пробки», снаружи, из нисходящего прохода, нижняя была замаскирована выпавшим случайно при работах Аль-Мамуна блоком известняка, да так что примерно 3000 лет считалось что в Большой Пирамиде иных помещений, кроме нисходящего прохода и подземной камеры, нет. Аль-Мамуну не удалось пробить эти пробки, и он просто выдолбил в более мягком известняке обход справа от них. Этот проход используется до сих пор, а пробки до сих пор никто не смог сдвинуть с места. По поводу пробок существует две основные теории, одна из них основывается на том, что восходящий проход имеет пробки, установленные в начале строительства и т.о, этот проход был запечатан ими с самого начала. Вторая утверждает, что имеющееся ныне сужение стен вызвано землетрясением, а пробки находились до этого в пределах Большой Галереи и были использованы для запечатывания прохода только после похорон фараона.

Важной загадкой этого участка восходящего прохода является то, что в том месте, где сейчас расположены пробки, в полноразмерной, хотя и укороченной модели ходов пирамиды — т. н. коридорах испытаний к северу от Большой Пирамиды — имеется стык сразу не двух, а трёх коридоров, третим из которых является вертикальный туннель. Поскольку пробки до сих пор никто не смог сдвинуть с места, вопрос есть ли над ними вертикальный лаз, остаётся открытым.

В середине восходящего прохода конструкция стен имеет особенность — в трёх местах установлены так называемые «рамочные камни» — то есть квадратный по всей длине проход пронзает насквозь три монолита. Назначение этих камней неизвестно.

Во вторую погребальную камеру от нижней части Большой галереи ведёт в южном направлении горизонтальный коридор длиной 35 м и высотой 1,75 м. Вторую камеру традиционно называют «Камерой царицы», хотя по обряду жён фараонов хоронили в отдельных маленьких пирамидах. «Камера царицы», облицованная известняком, имеет 5,74 метра с востока на запад и 5,23 метра с севера на юг; её максимальная высота 6,22 метра. В восточной стене камеры имеется высокая ниша.

Грот, Большая галерея и Палаты Фараона

Ещё одно ответвление от нижней части Большой галереи — узкая почти вертикальная шахта высотой около 60 м, ведущая к нижней части нисходящего прохода. Существует предположение, что она была предназначена для эвакуации рабочих или жрецов, завершавших «запечатывание» основного прохода к «Камере царя». Примерно посередине её находится небольшое, вероятнее всего, естественное расширение — «Грот» (Grotto) неправильной формы, в котором от силы могли бы поместиться несколько человек. Грот (12) расположен на «стыке» каменной кладки пирамиды и небольшого, высотой около 9 метров, холма на известняковом плато, лежащего в основании Большой Пирамиды. Стены Грота частично укреплены древней каменной кладкой, и поскольку отдельные её камни слишком велики, существует предположение что Грот существовал на плато Гиза как самостоятельное сооружение ещё задолго до строительства пирамид, а сама эвакуационная шахта строилась с учётом местонахождения Грота. Однако, с учётом того, что шахта именно долбилась в уже уложенной кладке, а не выкладывалась, о чём говорит её неправильное круглое сечение, встаёт вопрос о том как строителям удалось точно выйти на Грот.

Большая галерея продолжает восходящий проход. Её высота 8,53 м, это прямоугольный в сечении, с немного сужающимися кверху (т. н. «ложный свод») стенами, высокий наклонный туннель длиной 46,6 м. Посередине Большой галереи почти по всей длине, идёт правильное в сечении квадратное углубление размерами шириной 1 метр и глубиной 60 см, а на обоих боковых выступах имеется 27 пар углублений непонятного предназначения. Углубление заканчивается т. н. «Большой ступенькой» — высоким горизонтальным выступом, площадкой 1х2 метра, в конце Большой Галереи, непосредственно перед лазом в «прихожую» — Предкамеру. Площадка имеет пару аналогичных углублениям рампы, углублений по углам у стены (28-я и последняя пара углублений БГ.). Через «прихожую» лаз ведёт в облицованную чёрным гранитом погребальную «Камеру царя», где размещен пустой гранитный саркофаг.

Над «Камерой царя» находятся обнаруженные в XIX в. пять разгрузочных полостей общей высотой 17 м, между которыми лежат монолитные плиты толщиной около 2 м, а выше — двускатное перекрытие. Их назначение — распределять вес вышележащих слоёв пирамиды (около миллиона тонн), чтобы защитить от давления «Камеру царя». В этих пустотах обнаружены граффити, оставленные, вероятно, рабочими.

Вентиляционные каналы

От «Камеры царя» и «Камеры царицы» в северном и южном направлениях (сперва горизонтально, затем наклонно вверх) отходят так называемые «вентиляционные» каналы шириной 20-25 см. При этом каналы «Камеры царя», известные ещё с XVII в., сквозные, они открыты и снизу и сверху (на гранях пирамиды), тогда как нижние концы каналов «Камеры царицы» отделяет от поверхности стены около 13 см, они были обнаружены при простукивании в 1872 г. Верхние концы этих каналов не доходят до поверхности. Конец южного канала закрыт каменными «дверцами», обнаруженными в 1993 году с помощью телеуправляемого робота «Упуаут II» [1]. В 2002 году с помощью новой модификации робота «дверца» была пробурена, но за ней обнаружилась небольшая полость и ещё одна «дверца». Что находится дальше, пока неизвестно.
В настоящее время высказываются версии, что предназначение «вентиляционных» каналов носит религиозный характер и связано с представлениями египтян о загробном путешествии души.

Лодки фараона

Основная статья: Солнечная лодка

На сегодняшний день вблизи пирамид было обнаружено 7 ям с лодками. Во всех ямах настоящие древнеегипетские лодки были разобраны по частям. Первое из этих судов названых солнечные лодки, было обнаружено в 1954 году египетским архитектором Kamal el-Mallakh’ом и археологом Zaki Nur’ом. Лодка была из кедра и не имела ни единого следа от гвоздей для крепления элементов. Лодка состояла из 1224 частей, их удалось смонтировать реставратору Ahmed Yussef Mustafa только в 1968 году.

Размеры лодки: длина — 43,3 м, ширина — 5,6 м, а осадка — 1,50 м.

В настоящее время на южной стороне пирамиды Хеопса открыт для туристов музей этой лодки.

Страница: 0 , 1

en: Great Pyramid of Giza

de: Cheops-Pyramide

Примечания

См. также

• Египет
• Пирамида
• История Египта
• Фараон
• Александрия
• Каир
• Нил
• Хронология Древнего Египта
• Тутанхамон

Ссылки

• http://ru.wikipedia.org/wiki/Пирамида_Хеопса

Литература

• Ионина Н. А. 100 великих чудес света. — Москва, 1999.

---

Википедия Пирамида Хеопса адрес Викисловарь — адрес Викицитатник — адрес Викиучебник — адрес Викитека — адрес Викиновости — адрес Викиверситет — адрес Викигид — адрес

Выделить Пирамида Хеопса и найти в: Вокруг света Хеопса адрес Академик Хеопса/ru/ru/ адрес Астронет адрес Элементы Хеопса+&search адрес Научная Россия Хеопса&mode=2&sort=2 адрес Кругосвет Хеопса&results_per_page=10 адрес Научная Сеть Традиция — адрес Циклопедия — адрес Викизнание — Хеопса адрес

Google Bing Yahoo Яндекс Mail.ru Рамблер Нигма.РФ Спутник Google Scholar Апорт Онлайн-переводчик Архив Интернета Научно-популярные фильмы на Яндексе Документальные фильмы

Список ru-вики Вики-сайты на русском языке Список крупных русскоязычных википроектов Каталог wiki-сайтов Русскоязычные wiki-проекты Викизнание:Каталог wiki-сайтов Научно-популярные сайты в Интернете Лучшие научные сайты на нашем портале Лучшие научно-популярные сайты Каталог научно-познавательных сайтов НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

---

• Страница 0 — краткая статья
• Страница 1 — энциклопедическая статья
• Разное — на страницах: 2 , 3 , 4 , 5
• Прошу вносить вашу информацию в «Пирамида Хеопса 1», чтобы сохранить ее

Комментарии читателей:

Для статьи