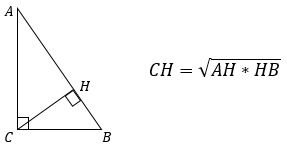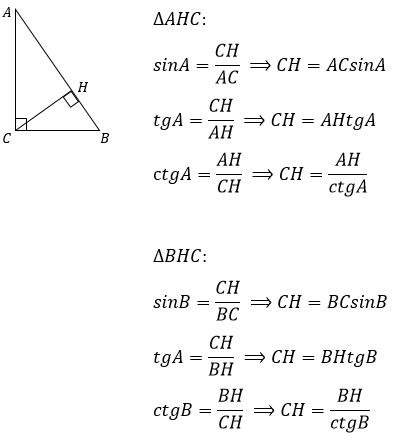Чтобы рассчитать кровельные материалы, необходим документ, который по ГОСТ 21.501-93 «Правила выполнения архитектурно-строительных чертежей» называется план кровли (крыши). Для корректного расчёта параметров достаточно вида крыши сверху с обозначенными направлениями скатов, длин проекций и высотными отметками.
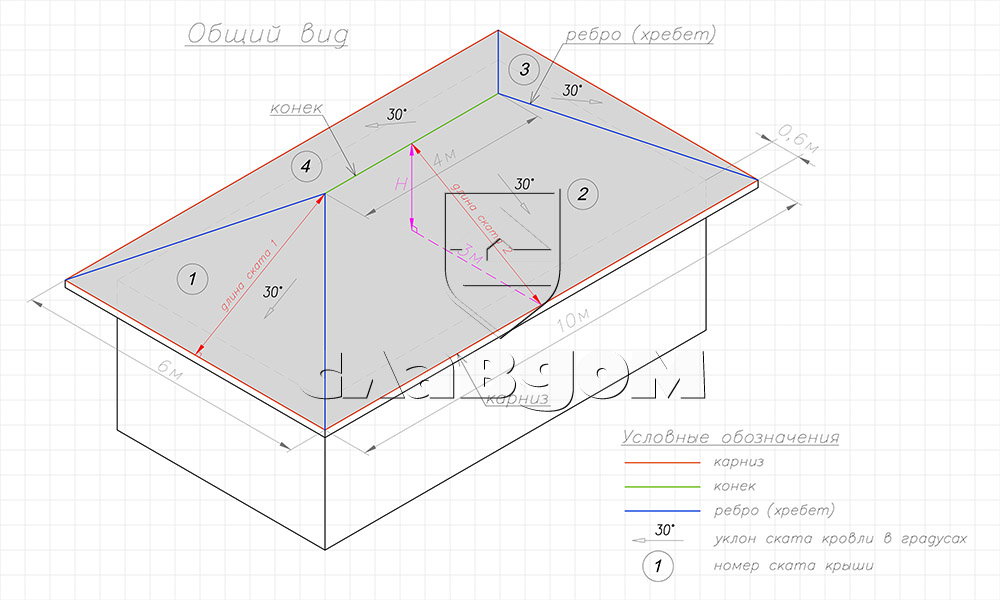
На рисунке представлен общий вид дома с конструкцией вальмовой крыши. Данный тип крыши состоит из 4-х скатов (плоскостей): два треугольных ската (вальмы) и две трапеции.
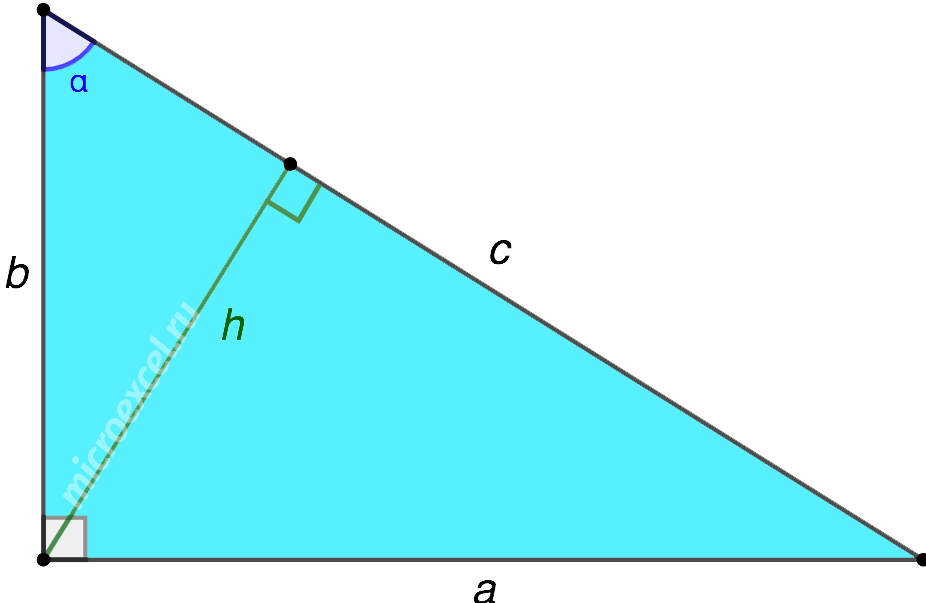
Для точного определения размеров кровли необходимо знать уклоны скатов кровли (крыши). Уклон ската – угол наклона ската по отношению к горизонту. Может выражаться в градусах, в процентах, дробях.
Если на плане кровли не указаны уклоны, измерить их можно с помощью транспортира по планам фасадов. С большей степенью точности можно вычислить, зная проекционные и высотные размеры кровли. Так как отношение этих двух величин постоянное для конкретного уклона, градусность будет определена предельно точно.
Интересные факты, известные из курса школьной геометрии:
- Если проекция ската равна изменению его высоты, уклон кровли будет равным 45 градусов;
- Длина ската, уклон которого равен 30-ти градусам в два раза больше его высоты. А длина ската с уклоном 60 градусов в два раза больше её проекции.
Для первого примера отношение высоты к проекции 1:1, а длина ската будет больше её проекции в 1,414 раза. Таким образом, 1,414 — коэффициент уклона ската с уклоном 45 градусов. Для уклона 60 градусов этот коэффициент равен 2,000, а для 30 – 1,155.
Следовательно, параметры ската в рамках конкретной кровли взаимосвязаны, и могут быть вычислены при известности двух из них.
Следующая задача, которую предстоит решать специалисту в ходе расчёта кровельных материалов, заключается в определении площади кровли, а так же суммарных длин всех её одноименных элементов: коньков, хребтов, карнизов. Для других конфигурация кровли могут быть ещё: ендовы, примыкания, фронтоны (щипцы, торцы) и так далее.
При определении площади следует разбить её на составляющие прямоугольники, треугольники, трапеции, при необходимости, круги и другие фигуры.
Относительно рассматриваемой крыши, план кровли разделён естественным образом на два треугольника и две трапеции.
На следующем рисунке планы кровли и двух основных фасада:
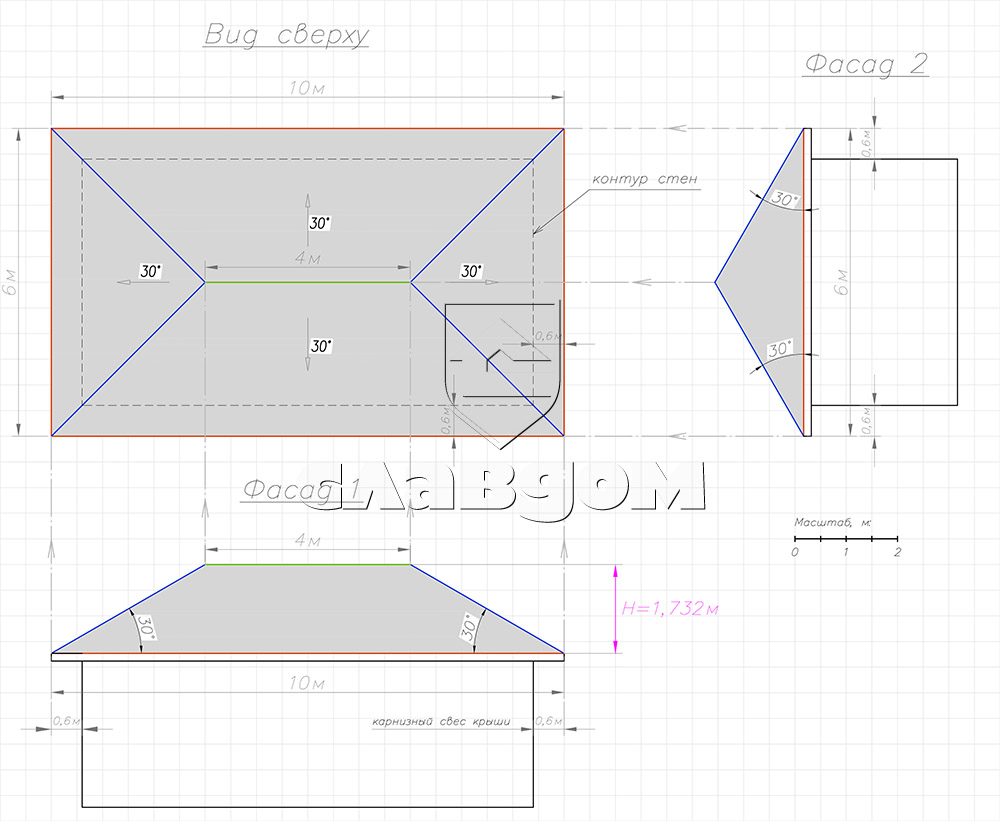
Приступим к расчету геометрических параметров крыши:
L карниза = (10 + 6 )*2 = 32 м
L конька = 4 м
Определим длины скатов. Они равны между собой исходя из плана кровли.
Смотрим на план кровли и видим, что длина ската по плану кровли составляет 3м. Однако это все же не искомая длина ската, а всего лишь проекция этой длины на горизонтальную плоскость.
Чтобы преобразовать проекцию длины в действительный размер достаточно умножить проекцию на коэффициент 1,155 (для 30 градусов):
L ската = 3м * 1,155 = 3,465 м.
Также, длину ската можно найти по теореме Пифагора, если известна высота крыши (H = 1,732 м):
(L ската) ² = H ² + (проекция длины ската) ² = (1,732) ² + (3) ² = 2,999824 + 9 =11,999824
L ската =3,465 м.
Найденная длина ската(скатов) является определяющей высотой фигур (трапеции и треугольника) при расчете площадей:
S кровли = Sската 1 + Sската 2 + Sската 3 + Sската 4
S ската 1 = Sската 3 и S ската 2 = Sската 4
По формуле площади треугольника:
S ската 1= (6*3,465)/2 = 10,395 м²
По формуле площади трапеции:
S ската 2 = ((10+4)/2)*3,465 = 24,255 м²
Итого общая площадь кровли:
S кровли = 10,395 + 10,395 + 24,255 + 24,255 = 67,3 м²
Есть самый быстрый способ определения нашей искомой площади, заключается он в умножении площади проекции крыши (габариты крыши по плану кровли, 6м х 10м) на коэффициент 1,155 (по аналогии с определением длины ската):
S кровли = 6*10*1,155 = 69,3 м²
Оставшийся параметр – длину ребра(хребта) можно также определить по теореме Пифагора:
( L ребра(хребта) ) ² = 3 2 + (длины ската) ² = ( 3 ) ² + (3,465) ² = 9 + 12,006225 = 21,006225
L ребра(хребта) = 4,583 м
Существует также коэффициент пересчета для определения искомых длин ребер, для этого достаточно умножить длину ребра(хребта) по плану кровли на коэффициент пересчета (30град./30град.), равным значению 1,08.
Итак:
(L проекции хребра(хребта)) ² = 3 2 +3 2 = 18
L проекции хребра(хребта) = 4,24264068711
L ребра(хребта) = 4,24264068711 *1,08 = 4,583 м
Сумма длин всех ребер(хребтов): L ребер(хребтов) = 4,583*4 = 18,332 м
После того как все геометрические параметры крыши определены, мы сможем подобрать и рассчитать любой кровельный материал по нашему выбору.
Вариант расчета кровли BRAAS, модель «Франкфуртская»:
(Минимальный рекомендуемый угол крыши для данной модели составляет 16 градусов, удовлетворяет нашим требованиям).
Внешние габариты одной черепицы «Франкфуртская» составляют 330х420мм.
Поскольку черепица укладывается с нахлестом и с учетом стыковки черепицы между собой через замковое соединение полезная площадь покрытия одной черепицы будет несколько меньше и составит 300х330мм.
Полезная площадь покрытия для всех видов черепиц всегда разная и обусловена широким разнообразием профилей и их размеров.
При размерах 300х330мм расход на 1м² составляет:
1м²/(0,3м * 0,33м) = 10,1шт./м²
Общее количество рядовой черепицы на покрытие всей крыши:
10,1*69,3 м² = 700 шт.
Принимая во внимание возможный бой черепицы при доставке/разгрузке/монтаже, а также некоторые отклонения в фактических размерах от данных в проекте, обязательно учитывается технологический запас материала. Величина запаса зависит от геометрической сложности кровли и должна приниматься индивидуально для каждого крыши. Для вальмовой крыши будет достаточно 5%. Запас очень важен при расчете кровельного покрытия, т.к. предостерегает нас от нехватки материала при монтаже кровли.
В итоге, с учетом запаса нам необходимо:
700 шт. + 5% = 735шт.
Количество начальной хребтовой черепицы:
4 шт.
Количество рядовой коньковой черепицы (расход 2,5шт./мп):
2,5*18,332 = 46 шт.
46 шт. — 4 шт. (начальные хребтовые) = 42 шт.
Вальмовая черепица: 2 шт. (устанавливается на место пересечения конька и двух ребер)
А теперь, предлагаем посмотреть как выглядит подробный расчет кровельного покрытия в нашей компании с учетом крепежа и всех необходимых аксессуаров:
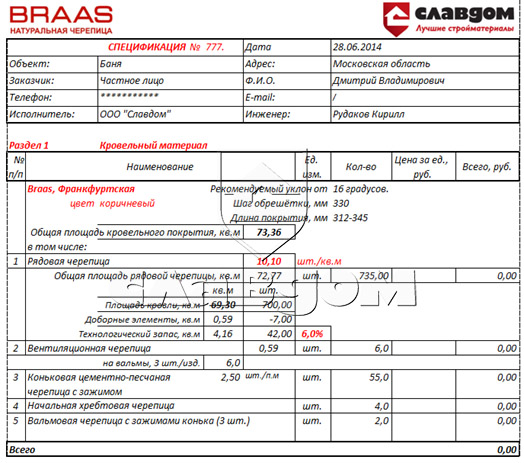
А также раздел 2 с крепежом и необходимыми аксессуарами:
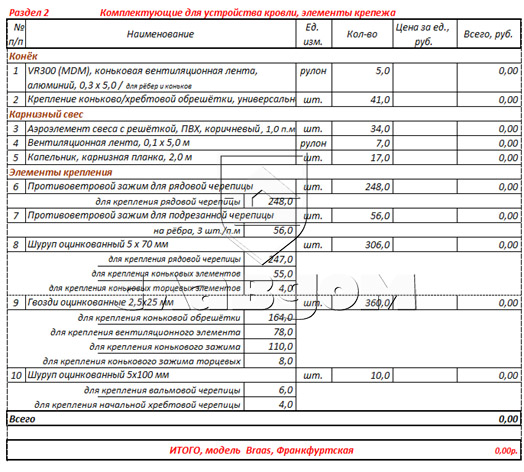
В данной статье мы разобрали с вами расчет скатной типовой крыши имея при себе лист бумаги, карандаш и немножко знаний из школьной программы геометрии. Сложные кровли с большим количеством скатов разных геометрических форм, сложных многоугольников, а также криволинейных поверхностей (конусов, сфер и т.д.) рассчитываются программно на ПК в специальных инженерных пакетах. Это в значительной мере облегчает процесс расчета, экономит время и предостерегает нас от возможных арифметических ошибок при расчете.
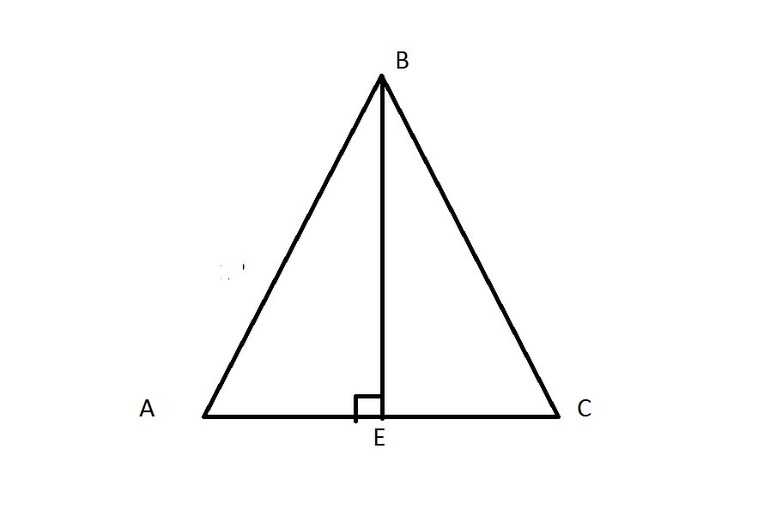
Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.

Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
1) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
или
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
или
Высота прямоугольного треугольника, проведенная к гипотенузе
Как и в любом треугольнике прямоугольный треугольник имеет три высоты. Две из них совпадают с катетами, а вот третья высота, проведенная к гипотенузе, постоянно будоражит наши умы.
Поэтому представляю вашему вниманию основные формулы для ее нахождения.
Начну с самой важной.
1. Высота, проведенная к гипотенузе равна корню квадратному из произведения проекций катетов на эту гипотенузу.
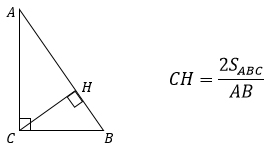
2. Высоту, проведенную к гипотенузе, можно найти, разделив удвоенную площадь прямоугольного треугольника на гипотенузу.
Такая формула получается из классический формулы нахождения площади треугольника: половина произведения основания на высоту, проведенную к этому основанию.
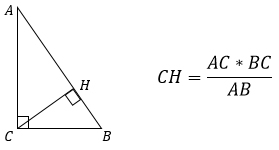
3. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на гипотенузу.
Эта формула получится из второй если заменить площадь на половину произведения катетов.
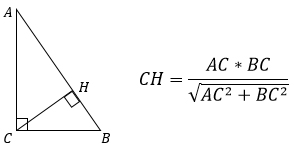
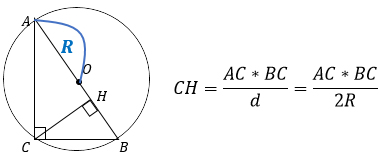
Т.к. АВ — гипотенуза, то ее можно выразить через катеты АС и ВС, используя теорему Пифагора. Тогда формула примет другой вид:
4. Высота, проведенная к гипотенузе, равна произведению катетов, деленному на диаметр описанной вокруг треугольника окружности (или на удвоенный радиус).
Так получается потому, что центр описанной окружности лежит в середине гипотенузы, значит, гипотенуза равна 2R или d.
5. Высоту, проведенную к гипотенузе, можно найти, используя геометрические определения синуса, тангенса и котангенса.
Надеюсь, что данная статья оказалась полезной!)
Готовься к экзамену вместе с нами! Заходи на нашу страницу в ВК.
Метод проекций при
составлении карт и планов заключается
в том, что точки физической поверхности
Земли А, В и
так далее проектируются отвесными
линиями на уровенную поверхность (см.
рис. 3, а,б).
Точки а, b
и так далее
называются горизонтальными проекциями
соответствующих точек физической
поверхности. Затем определяется положение
этих точек на уровенной поверхности с
помощью различных систем координат, и
тогда их можно нанести на лист бумаги,
т. е. на лист бумаги будет нанесен отрезок
ab,
который
является горизонтальной проекцией
отрезка AВ.
Но, чтобы по
горизонтальной проекции определить
действительное значение отрезка AВ,
необходимо
знать длины аА
и bВ
(см. рис.
3, б),
т.е. расстояния от точек A
и В до
уровенной поверхности. Эти расстояния
называются абсолютными
высотами
точек местности.
Таким образом,
задача составления карт и планов
распадается на две:
определение
положения горизонтальных проекций
точек;
определение высот
точек местности.
При проектировании
точек на плоскость, а не на уровенную
поверхность, появляются искажения:
вместо отрезка ab
будет отрезок
а’b‘
вместо высот
точек местности аА
и bВ
будут а’А
и b‘В
(см. рис. 3, а,б).
Итак, длины
горизонтальных проекций отрезков и
высоты точек будут различны и при
проектировании на уровенную поверхность,
т.е. при учете кривизны Земли, и при
проектировании на плоскость, когда
кривизна Земли не учитывается (рис. 4).
Эти различия будут наблюдаться в длинах
проекций S
= t
– S,
в высотах точек h
= b‘О
– bО
= b‘О
– R.
в настоящее время
относительная погрешность
Балтийская
система высот
(БСВ) — принятая в СССР
в 1977
году
система абсолютных
высот,
отсчёт которых ведётся от нуля футштока
в Кронштадте.
От этой отметки отсчитаны высоты опорных
геодезических
пунктов,
которые обозначены на местности разными
геодезическими
знаками
и нанесены на карты.
В настоящее время
БСВ используется в России и ряде других
стран СНГ.
Абсолютная
высота, или абсолютная отметка
(в геодезии) — расстояние (в метрах)
по вертикали от какой-либо точки на
поверхности Земли
до среднего уровня поверхности океана,
не нарушенного волнением и приливами,
или до поверхности геоида.
Абсолютная
высота представляет собой третью
координату точки, дополняющую широту
и долготу;
на суше определяется при помощи
нивелирования.
Абсолютная высота точки, лежащей выше
уровня
океана,
считается положительной, ниже —
отрицательной.
При
съёмке местности используют географические
координаты
и абсолютную высоту ближайших опорных
геодезических пунктов.
В России
абсолютные высоты точек земной поверхности
отсчитывают от среднемноголетнего
уровня Балтийского
моря,
определённого от нуля футштока
в Кронштадте.
Относительная
высота
— топографическое
превышение какой-либо точки земной
поверхности относительно другой точки,
отсчитываемое по вертикали, равное
разности абсолютных
высот
этих точек (например, высота горной
вершины над уровнем дна ближайшей
долины); расстояние по вертикали от
указанного исходного уровня до уровня,
точки или объекта, принятого за точку.
Соседние файлы в предмете Геодезия
- #
28.12.201376.15 Кб301Работа №2 Вариант 1.dwg
- #
28.12.201366.58 Кб193Работа №2 Вариант 2.dwg
- #
28.12.201390.08 Кб185Работа №2 Вариант 3.dwg
- #
- #
- #
- #
Как построить высоту треугольника — основные способы
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.
- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
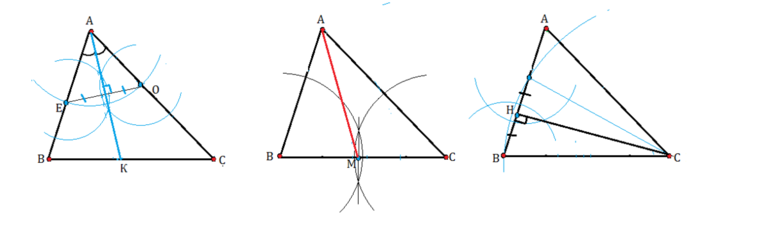
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
Проекции катетов на гипотенузу
Так как высота, проведенная к гипотенузе, представляет собой проведенный к ней перпендикуляр, то катеты — это наклонные, а отрезки гипотенузы, на которые делит ее высота — проекции катетов на гипотенузу прямоугольного треугольника.
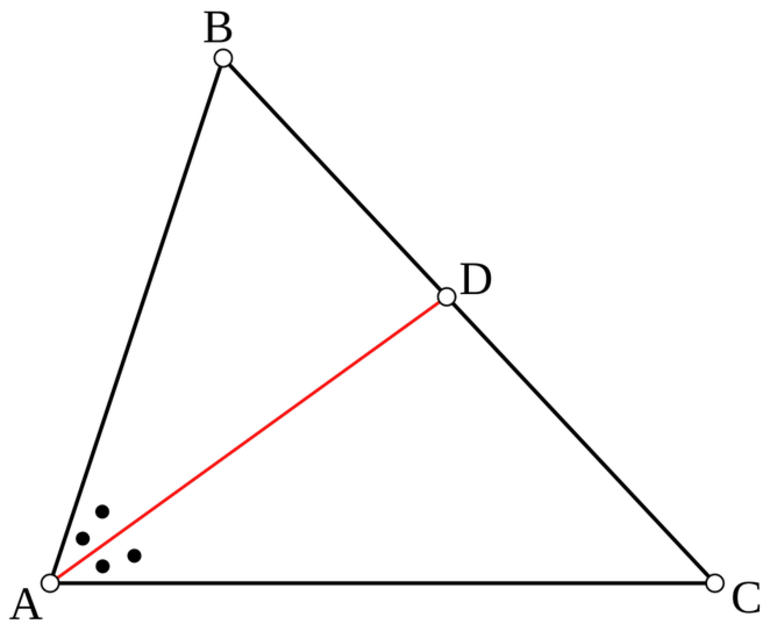
В треугольнике ABC, изображенном на рисунке, AD — проекция катета AC на гипотенузу AB, BD — проекция катета BC на гипотенузу.
Катеты, их проекции на гипотенузу, гипотенуза и высота прямоугольного треугольника связаны между собой формулами.
1) Свойство высоты, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее геометрическое (среднее пропорциональное) между проекциями катетов на гипотенузу.
2) Свойства катетов прямоугольного треугольника.
Катет прямоугольного треугольника есть среднее геометрическое (среднее пропорциональное) между гипотенузой и проекцией этого катета на гипотенузу.
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.
Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
2. Через длины сторон треугольника:
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :
Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше: