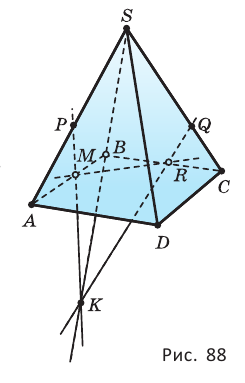
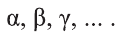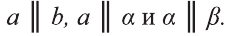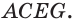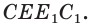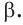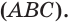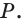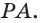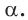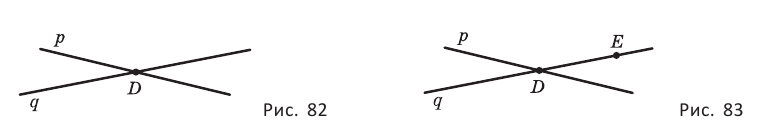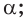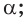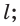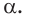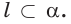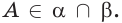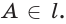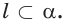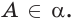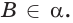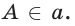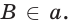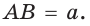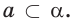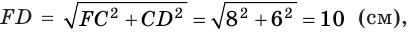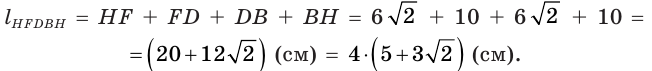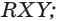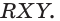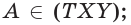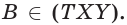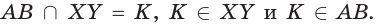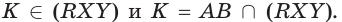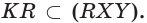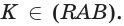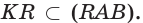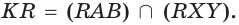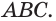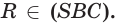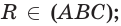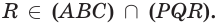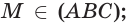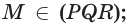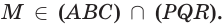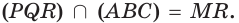§ 1. Пространственные фигуры
Стереометрия — раздел геометрии, в котором изучаются пространственные фигуры.
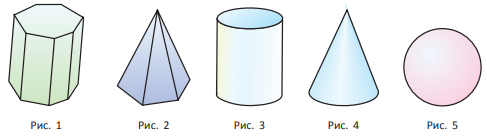
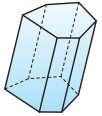
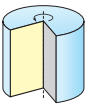
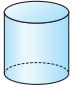
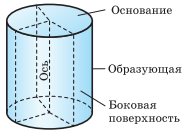
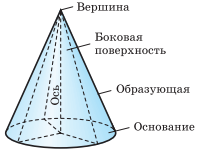
Примеры некоторых пространственных фигур — призма (рис. 1), пирамида (рис. 2), цилиндр (рис. 3), конус (рис. 4), шар (рис. 5).
Представление пространственной фигуры на рисунке (невидимые линии делают штриховыми) называют изображением фигуры.
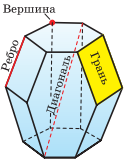
Многогранники — тела, ограниченные плоскими многоугольниками. Эти многоугольники называются гранями многогранника, их вершины — вершинами многогранника, а стороны — рёбрами многогранника. Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника.
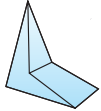
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой своей грани. На рисунке справа изображён невыпуклый многогранник.
Призма
Призмой называется многогранник, две грани которого — равные n-угольники, а остальные n граней — параллелограммы.
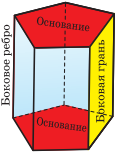
Равные грани-многоугольники призмы называются её основаниями, а остальные грани — боковыми гранями. Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами.
В зависимости от количества сторон основания призмы отличают треугольную, четырёхугольную, пятиугольную и т. д. призмы. На рисунке справа изображена шестиугольная призма.
Совокупность боковых граней призмы образуют боковую поверхность. Площадь боковой поверхности призмы равна сумме площадей боковых граней.
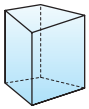
Прямая призма — призма, боковые грани которой являются прямоугольниками. Обычно, изображая прямую призму, её боковые рёбра проводят вертикально.
Призма прямая, если боковые рёбра перпендикулярны рёбрам основания призмы. Призма наклонная, если боковые рёбра не перпендикулярны рёбрам основания призмы.
Прямая призма называется правильной, если её основания являются правильными многоугольниками.
Призма, основаниями которой являются параллелограммы, называется параллелепипедом.
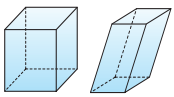
Параллелепипед, как и призма, может быть и прямым, и наклонным (см. рис.).
Прямой параллелепипед, основания которого являются прямоугольниками, называется прямоугольным параллелепипедом. Все грани прямоугольного параллелепипеда являются прямоугольниками.
Три ребра прямоугольного параллелепипеда, сходящиеся в одной вершине, называются измерениями прямоугольного параллелепипеда.
Задача 1. ABCDA1B1C1D1 — прямоугольный параллелепипед (см. рис.), измерения которого равны 2, 3 и 5. Найдите длину пространственной ломаной B1A1ADC.
Видеорешение
Задача 2. Найдите площадь полной поверхности прямоугольного параллелепипеда с измеренями 6, 15 и 20 см.
Видеорешение
Прямоугольный параллелепипед с равными измерениями называется кубом. Все грани куба — равные друг другу квадраты.
Пирамида
Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные являются треугольниками с общей вершиной.
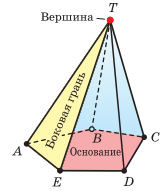
На рисунке справа изображена пирамида TABCDE. Многоугольник ABCDE называют основанием пирамиды, треугольные грани ATB, BTC, CTD, DTE, ETA — боковыми гранями, а общую вершину T боковых граней — вершиной пирамиды. Обычно в записи обозначения пирамиды первая буква соответствует её вершине.
В зависимости от количества сторон основания пирамиды отличают треугольную, четырёхугольную, пятиугольную (см. рис. выше) и т. д. пирамиды.
Пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр, называется правильной.
Высота боковой грани правильной пирамиды, опущенная из вершины пирамиды, называется апофемой пирамиды.
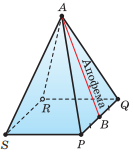
На рисунке справа изображена правильная четырёхугольная пирамида APQRS, отрезок AB — одна из её апофем.
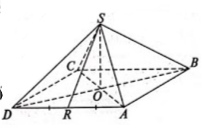
Задача 3. На рисунке изображена правильная четырехугольная пирамида. Среди отрезков AD, AC, SR, SA, SO укажите отрезок, который является апофемой правильной четырехугольной пирамиды..
Видеорешение
Теорема 1. У правильной пирамиды равны её:
а) боковые грани;
б) апофемы.
Теорема 2. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.
Цилиндр
Цилиндром называется тело, полученное вращением прямоугольника вокруг одной из его сторон.
При этом вращении одна сторона прямоугольника остаётся неподвижной, её называют осью цилиндра. Сторона, противолежащая оси, образует поверхность, которую называют боковой поверхностью цилиндра, а саму сторону — образующей цилиндра. Ещё две стороны прямоугольника при вращении образуют поверхности, которые являются равными кругами, эти круги называют основаниями цилиндра.
Конус
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов, который называют осью конуса.
Второй катет описывает круг, который называют основанием конуса; неподвижную вершину треугольника, которая не принадлежит основанию, называют вершиной конуса. Гипотенуза при вращении образует поверхность, которую называют боковой поверхностью конуса, саму гипотенузу называют образующей конуса.
Шар
Шаром называется тело, полученное вращением круга вокруг своего диаметра. При этом вращении окружность описывает поверхность, которую называют сферой.
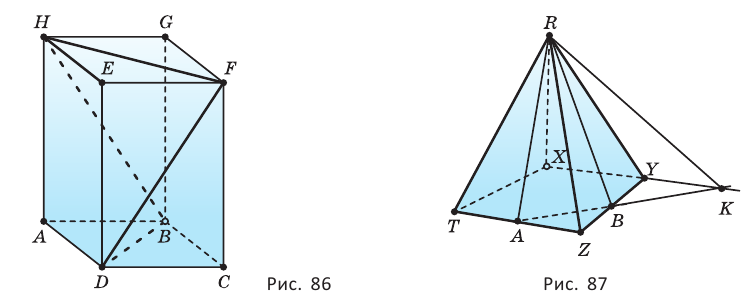
Задание.Дан куб ABCDA1B1C1D1. Если длина пространственной
ломаной ABB1C1C равна 12√2, то длина ребра куба равна
Варианты ответов.
1)
3;
2) 3√2;
3) 4√2;
4) 2√2;
5)
4.
Анализ. Пространственная ломаная
состоит из четырех отрезков, каждый из которых является ребром куба и все они
равны между собой, так как все ребра куба равны
Решение. Обозначим ребро куба за a, то длина пространственной
ломаной равна 4a=12√2, откуда a=12√2/4=3√2 – длина ребра.
Ответ. 2
Ломаная линия
- Замкнутая и незамкнутая ломаная
- Самопересекающаяся ломаная
- Длина ломаной
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
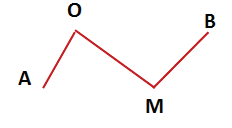
Построим ломаную из четырёх отрезков:
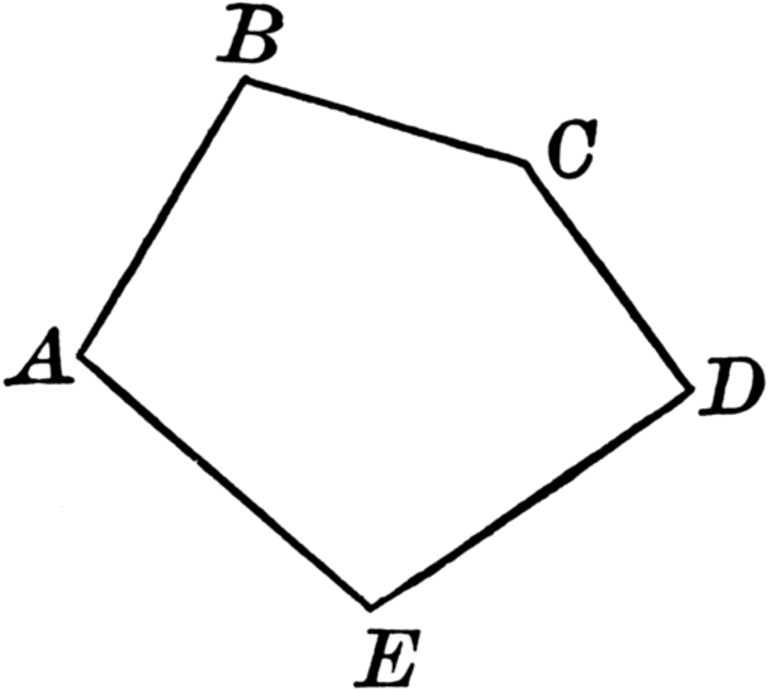
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE
или ломаная EDCBA
.
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:
многоугольник ABCDE.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
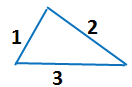
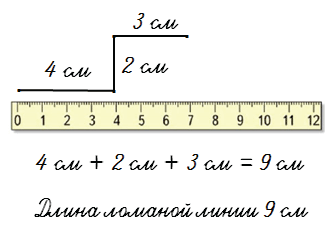
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
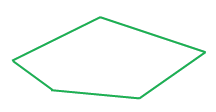
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ответ: 17 см.
Содержание:
Прямые и плоскости в пространстве
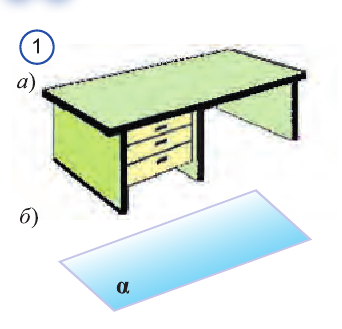
Основные геометрические фигуры в пространстве: точка, прямая и плоскость. Плоскость мы представляем в виде поверхности стола (рис. 1 а). Плоскость как и прямая бесконечна. На рисунке представляем только часть плоскости (рис. 1 б). Однако, мы предполагаем, что се можно продолжить в любую сторону и на чертеже изображаем в виде параллелограмма (рис. 1 б). Плоскости обозначаем прописными греческими буквами
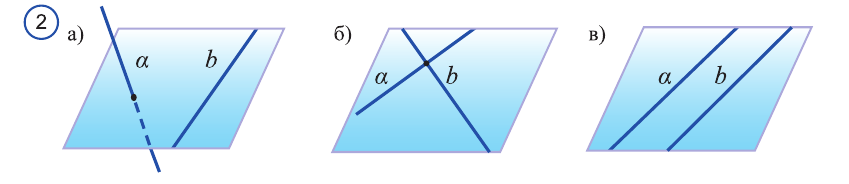
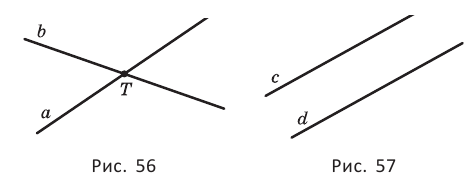
Две прямые в пространстве могут пересекаться или не пересекаться (рис. 2). В пространстве две прямые, не лежащие в одной плоскости, называются скрещивающимися (рис. 2 а).
Прямые, лежащие в одной плоскости и имеющие только одну общую точку, называются пересекающимися прямыми (рис. 2 б).
Прямые, лежащие в одной плоскости и непересекающиеся, называются параллельными прямыми (рис. 2 в).
Примером скрещивающихся прямых могут быть две дороги, одна из которых проходит по эстакаде, а другая под эстакадой (рис. 3). Точно также, прямые, на которых лежат ребра MN и 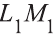
Как расположены относительно друг друга прямая и плоскость в пространстве?
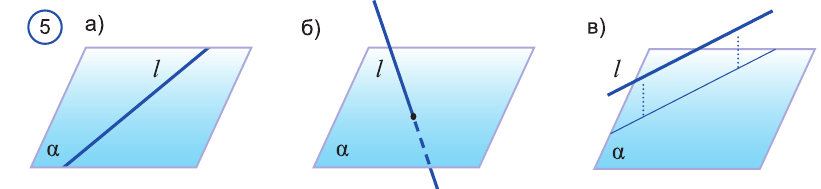
Прямая может лежать на плоскости (рис. 5.а), пересекать ее (рис. 5.6) или не пересекать, то есть иметь или не иметь с плоскостью общую точку (рис. 5.в). В последнем случае говорят, что прямая параллельна плоскости.
Точно также, прямая, содержащая диагональ АЕ параллелепипеда AGEC (рис. 6.г), лежит в плоскости основания, пересекает плоскость грани 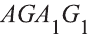
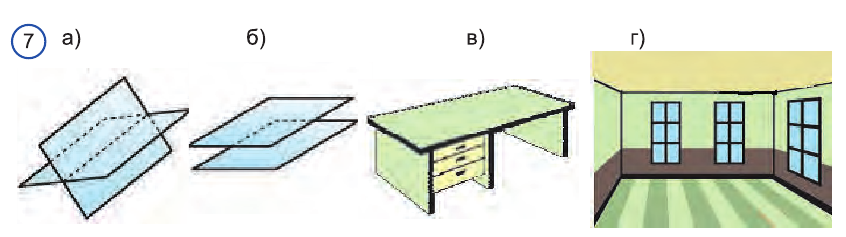
Теперь рассмотрим взаимное расположение плоскостей в пространстве. В пространстве плоскости могут пересекаться по прямой (рис. 7 а) или не иметь общих точек (рис. 7 б). Тогда говорят, что эти плоскости соответственно пересекаются или параллельны.
Крышка стола и его боковушка, изображенные на рисунке 7в дают представление о пересекающихся плоскостях, а пол и потолок в помещении (рис. 7 г) — о параллельных плоскостях.
Аналогично, не противоположные боковые грани параллелепипеда (рис. 4), дают представление о пересекающихся плоскостях, а его верхняя и нижняя грани и противоположные боковые грани — о параллельных плоскостях.
Знаки параллельности — » ||» используют не только для параллельных прямых, но и для параллельных прямой и плоскости и для параллельных плоскостей:
В стереометрии, как и в планиметрии некоторые геометрические свойства фигур принимают без доказательств. Следующие свойства плоскостей называем группой аксиом С и принимаем их без доказательств.



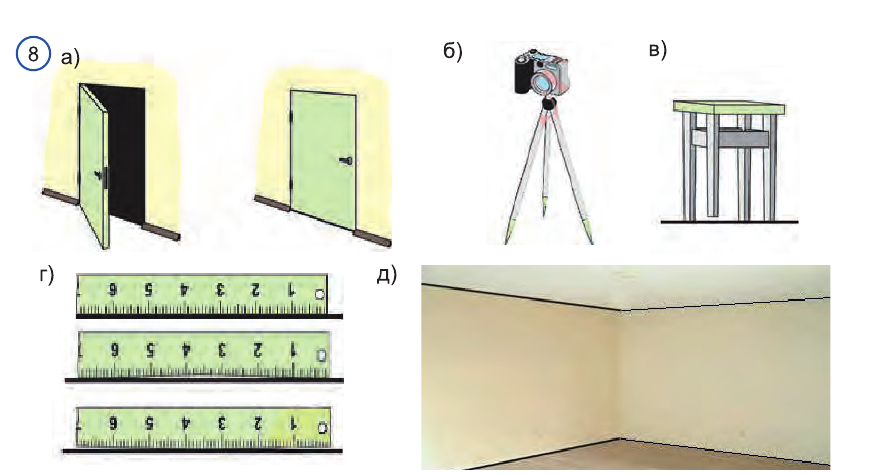
Активизирующее упражнение. На какие аксиомы можно сослаться при объяснении следующих случаев на рисунке 8?
Эти три аксиомы вместе с введенными в планиметрии аксиомами являются основой стереометрии. Необходимо напомнить, что все фигуры, рассматриваемые в планиметрии, считались расположенными в одной плоскости. В стереометрии таких плоскостей бесконечно много и пред-полагается, что на каждой из них имеют место все аксиомы планиметрии и все доказанные в ней свойства. Поэтому, аксиомы планиметрии в курсе стереометрии рассматриваются с точки зрения стереометрии.
Теорема 2.1 Через прямую и не лежащую па ней точку можно провести одну и только одну плоскость.
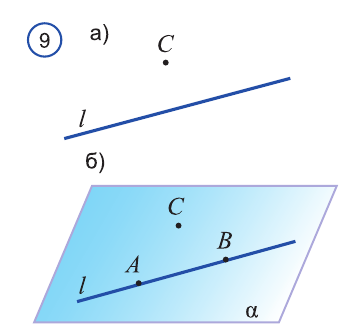
Доказательство. Пусть l — заданная прямая, а С точка, не лежащая на ней (рис. 9 а). Сначала докажем существование плоскости, о которой говорится в заключении.
Отметим на прямой l точки А и В. По условию точки А, В и С не лежат на одной прямой. Тогда по аксиоме через точки А, В и С можно провести плоскость а (рис. 9 б). А по аксиоме С2 плоскость а проходит через прямую l. Следовательно, а — искомая плоскость..
Теперь докажем, что эта плоскость единственна.
Предположим обратное: Пусть через данную прямую l и не лежащую на ней точку С можно провести еще одну плоскость 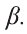
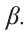
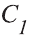
Следовательно, наше предположение неверно. Через прямую и не лежащую на ней точку можно провести одну и только одну плоскость.
Теорема 2.2 Через две пересекающиеся прямые можно провести единственную плоскость.
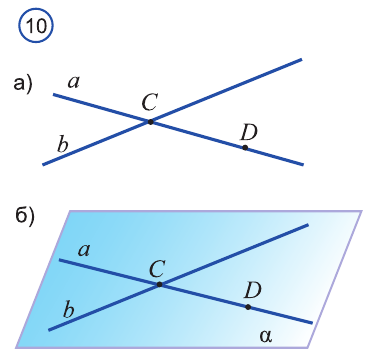
Доказательство. Пусть прямые а и b пересекаются в точке С (рис. 10 а).
Отмстим на прямой а точку D, отличную от точки С. Тогда по доказанной теореме 1 через прямую b и не лежащую на ней точку D проходит единственная плоскость (рис. 10 б). Эта плоскость проходит через прямую а и точки С и D, лежащие на ней. Тогда, по аксиоме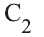
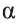
Докажите единственность этой плоскости самостоятельно.
Прямые и плоскости
А) Прямые и плоскости в пространстве могут располагаться по-разному.
Две прямые плоскости могут иметь только одну общую точку. Такие прямые называются пересекающимися. На рисунке 56 показаны пересекающиеся прямые 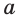
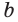
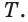
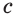
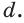
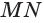
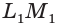
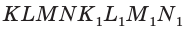
Каким может быть взаимное расположение прямой и плоскости?
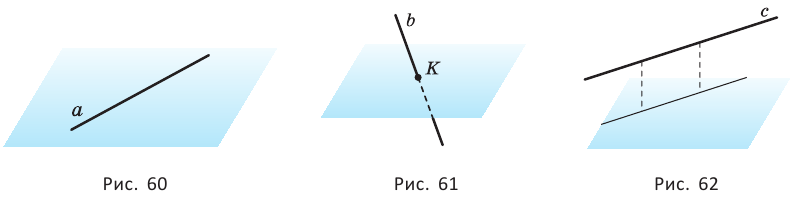
Прямая может лежать в плоскости (рис. 60). Если прямая не лежит в плоскости, то она может пересекать её в некоторой точке (рис. 61) или не иметь с плоскостью ни одной общей точки (рис. 62). В последнем случае прямая и плоскость называются параллельными.
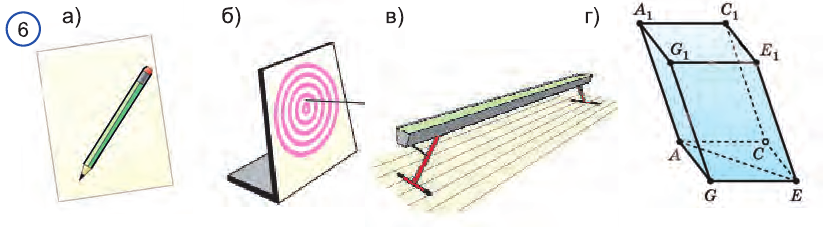
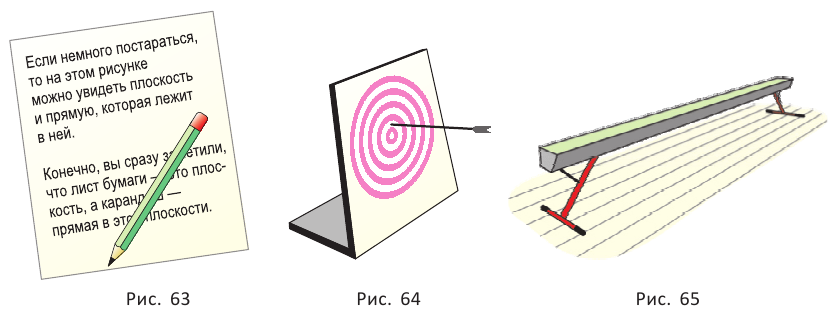
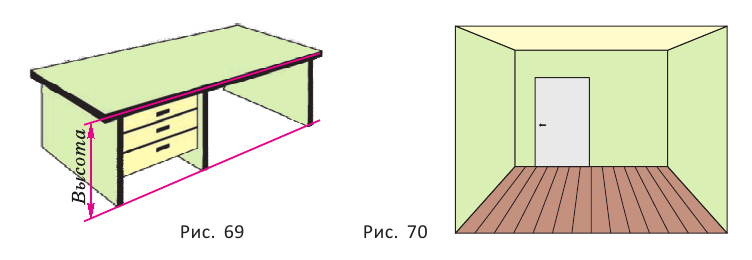
Представление о прямой, лежащей в плоскости, даёт карандаш, который лежит на столе (рис. 63), о пересекающихся прямой и плоскости — стрела, выпущенная из лука и попавшая в плоскую мишень (рис. 64), о прямой, не пересекающей плоскость, — пол в спортивном зале и гимнастическое бревно (рис. 65).
Указанные виды взаимного расположения прямой и плоскости можно проследить и на изображении параллелепипеда (рис. 66). Прямая, которой принадлежит диагональ 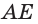
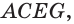
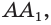
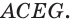
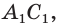
Как могут располагаться в пространстве две плоскости
Плоскости могут пересекаться по прямой (рис. 67) или не иметь общих точек (рис. 68). В соответствии с этим их называют пересекающимися или параллельными.
Представление о пересекающихся плоскостях дают столешница и боковина стола (рис. 69), о параллельных плоскостях — пол и потолок в помещении (рис. 70). На изображении параллелепипеда на рисунке 66 пересекающимися являются плоскости граней 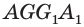
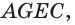
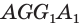
Знак 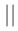
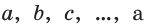
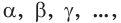

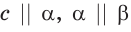
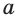
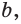
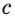
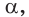
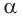
Б) Теория взаимного расположения прямых и плоскостей в пространстве основывается на следующих аксиомах.
- Аксиома 1. Если три точки не лежат на одной прямой, то через них проходит единственная плоскость.
- Аксиома 2. Если две точки прямой лежат в плоскости, то каждая точка этой прямой принадлежит плоскости. В этом случае говорят, что прямая лежит в плоскости.
- Аксиома 3. Если две плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.
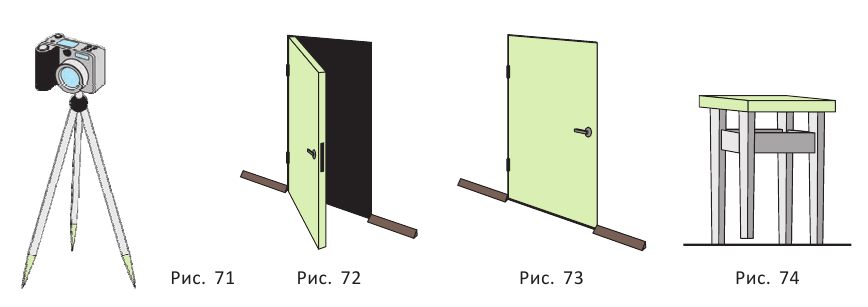
Свойство плоскости, которую фиксирует аксиома 1, часто используется на практике. Острия ножек штатива фотоаппарата (рис. 71) принадлежат одной плоскости, и поэтому положение фотоаппарата устойчивое. Дверь, закреплённая на двух петлях, не занимает определённого положения (рис. 72), но если добавить третью точку крепления — замок, то положение двери фиксируется (рис. 73). Когда ножки табурета неправильно подрезаны, то табурет стоит на трёх ножках, а четвёртая ножка висит над полом (рис. 74).
Свойство плоскости, зафиксированное аксиомой 3, проявляется при пересечении двух смежных стен комнаты (рис. 78).
Отметим, что в стереометрии выполняются все аксиомы планиметрии и все доказанные в ней утверждения. В частности, признаки равенства и признаки подобия треугольников остаются в силе и для треугольников, лежащих в разных плоскостях.
В соответствии с аксиомой 1 плоскость определяется тремя своими точками 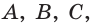
- Заказать решение задач по высшей математике
Пример №1
На рёбрах 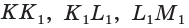
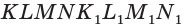
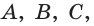
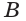
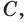
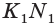
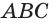
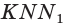
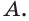
Точка 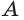
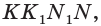
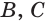
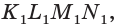
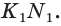
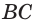
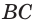
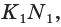
Точка 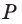
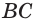
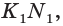
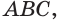
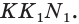
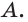
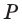
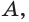
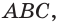
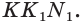
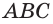
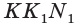
Теорема 3. Через прямую и точку вне её проходит единственная плоскость.
Доказательство: Пусть есть прямая 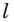
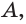
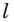
Выберем на прямой 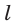
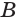
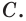
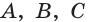
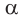
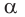
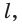
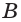
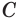
Допустим, что через прямую 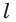
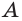
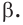
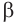
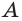
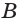
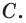
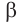
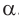
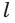
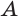
Теорема 4. Через две пересекающиеся прямые проходит единственная плоскость.
Доказательство: Пусть имеются две пересекающиеся прямые 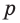
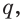
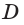
Выберем на прямой 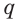
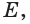
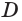
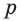
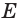
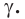
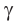
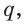
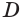
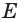
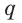
Допустим, что через прямые 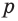
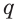
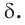
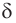
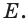
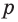
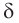
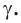
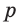
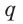
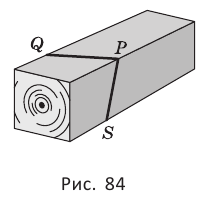
Теорема 4 находит своё применение на практике. Если столяру нужно распилить брусок под определённым углом, он, чтобы наметить плоскость распила, проводит в двух смежных гранях бруска пересекающиеся прямые 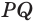
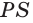
Пример №2
Докажите, что:
а) если некоторая точка 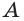
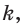
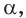
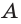
б) если две точки 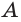
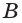
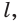
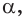
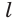
в) если плоскости 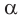
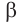
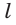
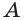
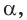
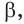
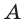
г) прямая 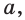
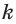
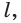
Решение:
a) 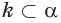
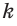
Любая точка прямой 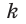
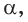
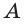
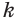
б) 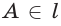
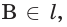
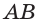
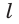
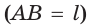
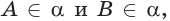
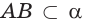
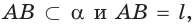
в) 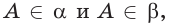
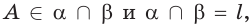
г) 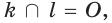
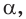
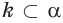
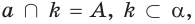
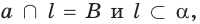
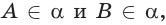
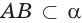
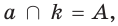
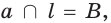
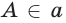
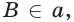
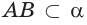
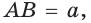
Пример №3
Основанием прямоугольного параллелепипеда 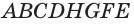
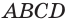

Решение:
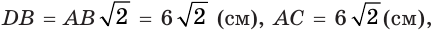
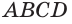
так как 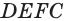
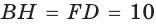
Ответ: 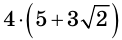
Пример №4
Точки 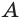
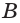
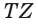
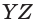
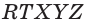
а) точку пересечения прямой 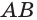
б) прямую, по которой пересекаются плоскости 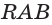
Решение:
а) 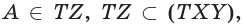
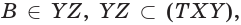
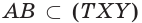
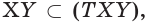
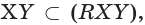
б) 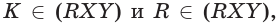
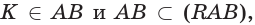
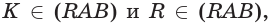
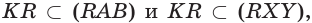
Пример №5
Точки 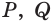
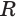
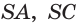
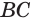
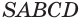
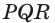
Решение:
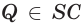
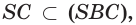
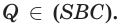
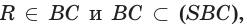
По аксиоме 2
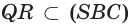
поэтому
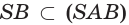
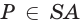
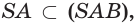
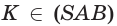
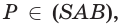
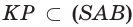
поэтому
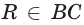
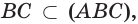
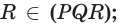
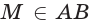
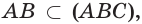
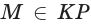
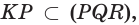
тогда
По аксиоме 3
Пространственное моделирование
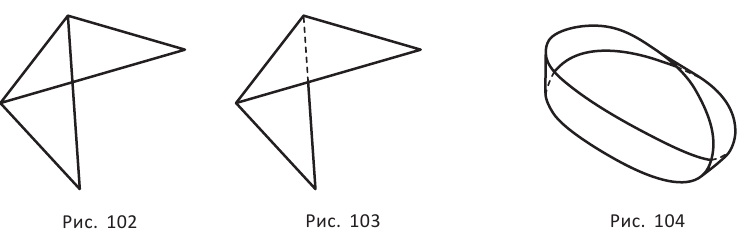
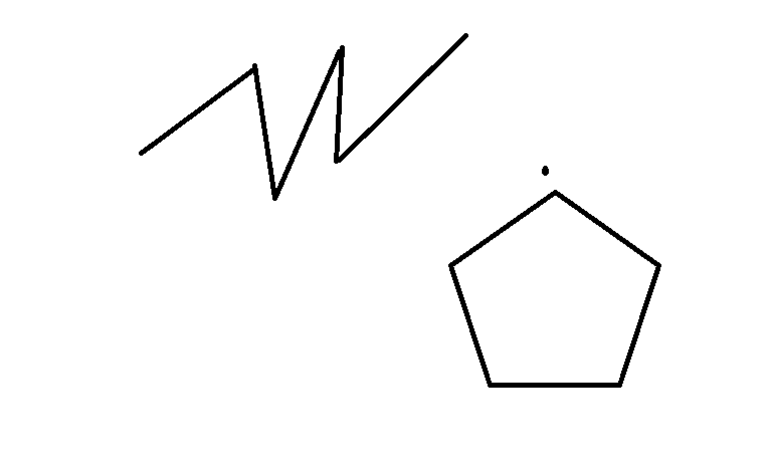
Ответьте, какая — плоская или пространственная — фигура изображена на рисунке:
а) 102; б) 103; в) 104.
На рисунке 104 изображена поверхность, которую называют лентой Мёбиуса, или листом Мёбиуса. Её открыли независимо друг от друга в 1858 году немецкие математики Август Мёбиус и Иоганн Листинг. До этого считалось, что любая поверхность имеет две стороны, которые можно окрасить в разный цвет.
Лента Мёбиуса имеет одну сторону и один край. В этом легко убедиться. Возьмём прямоугольную ленту 
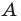
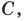
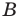
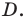
Какая поверхность получится, если лист Мёбиуса разрезать по его средней линии? Попробуйте окрасить эту поверхность. Что получилось? А что будет, если лист Мёбиуса разрезать, отступив от его края на третью часть ширины?
Памятный знак «Лист Мёбиуса» (рис. 105) был установлен 22 января 2009 года к 80-летию Национальной академии наук Беларуси.
Свойства ленты Мёбиуса нашли практическое применение и в промышленности. В виде ленты Мёбиуса изготавливают шлифовальные ленты, красящую ленту матричных принтеров, полосу ленточного конвейера, что позволяет увеличить срок службы, потому что вся поверхность ленты равномерно изнашивается. Ленту Мёбиуса применяют в системах записи на непрерывную плёнку, чтобы удвоить время записи.
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Геометрические задачи и методы их решения
Ломаная линия
Ломаная линия состоит из отрезков — звеньев.
Конец одного отрезка — начало другого. Никакие два соседние звена не лежат на одной прямой.
Концы каждого звена — это вершины. Их можно обозначать буквами.
Ломаная линия бывает незамкнутая.
Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.
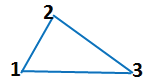
Такая замкнутая ломаная линия называется треугольником.
У нее три вершины.
У треугольника три звена.
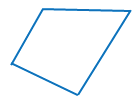
Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.
Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.
Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.
Поделись с друзьями в социальных сетях:
Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA .
Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
Ломаная линия — определение, виды и примеры построения фигуры
Краткое описание
Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.
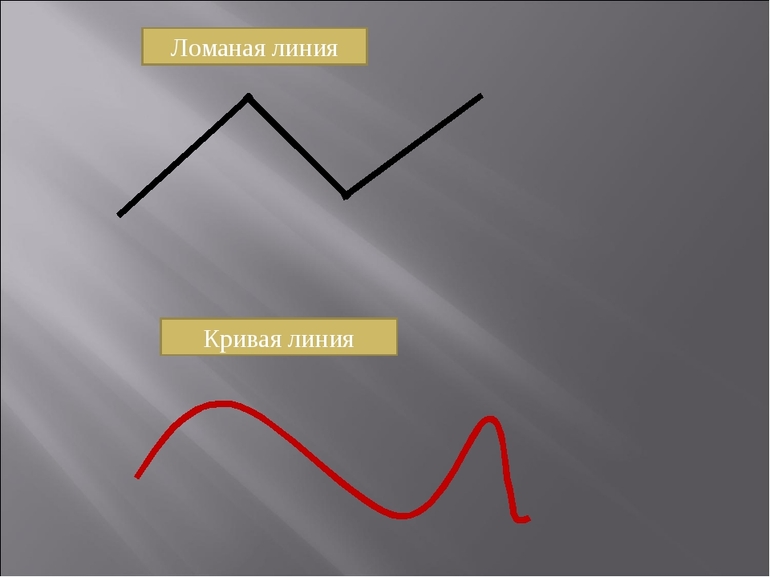
Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.
В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.
Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.
Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.
Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.
Некоторые математические примеры касаются изогнутой линии с самопересечениями (пятиконечная звезда). К этой категории также можно отнести зигзаг, в котором каждый второй отрезок параллелен другому, а последние формируют одинаковый угол.
Математическое определение
Ломанной принято называть ту геометрическую фигуру, которая состоит из обычных отрезков (R1, R2, R3 и R4, Rn-1 Rn). Вершинами изогнутой принято называть точки R1…Rn, а вот все остальные отрезки — это неотъемлемые звенья. Если для любого w действует формула <1, 2, n — 2>, а отрезки не расположены на одной прямой, то такая ломанная будет называться невырожденной. В противном случае придётся иметь дело с вырожденным примером.
Для лучшего усвоения этой темы следует рассмотреть несколько примеров. Изогнутая может иметь самопересечение, но это возможно только в том случае, если минимум два отрезка обладают общей точкой (за исключением вершины).
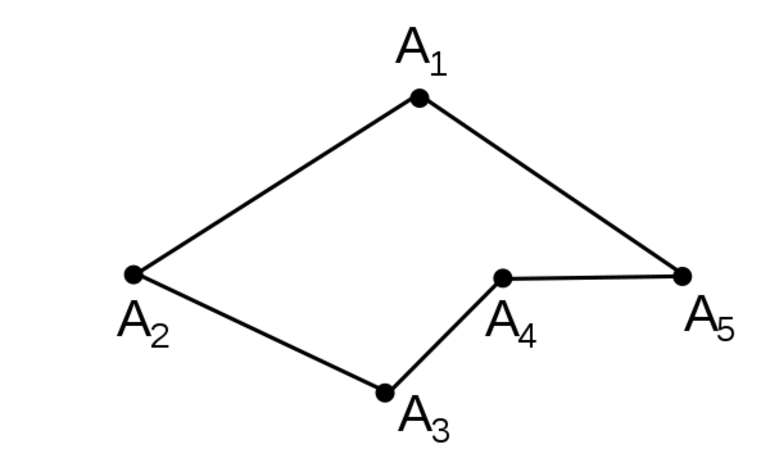
В математике часто можно встретить фигуру, которая является обычной ломаной линией. В этом случае практикуется применение следующей записи: R1R2R3R4R5R6. Если ученику предстоит разобраться со всеми нюансами построения замкнутой ломаной из трёх звеньев и более, тогда ему понадобятся вспомогательные отрезки (к примеру: R1, R2, а также Rn -1 Rn, которые не должны лежать на одной прямой).
Замкнутую плоскую ломаную линию принято называть многоугольником. Если рассматривать многогранники, то все стороны фигуры будут называться рёбрами. Учителя России предпочитают создавать краткосрочное планирование по этой теме, так как в этом случае можно донести больше полезной информации до учеников.
Гораздо проще разобраться с изгибами зигзага, так как они используются в швейном деле, в распространённом декоративном оформлении предметов обихода в качестве орнамента. Стоит отметить, что изогнутая линия нашла широкое применение в различных отраслях:
- Архитектура. Изогнутые линии позволяют сооружать интересные номера.
- Картография (тщательное проектирование маршрутов и подробное схематическое изображение всех улиц).
- Химическая отрасль (различные соединения и своеобразные молекулярные структуры).
- Востребованный дизайн ландшафтов (утончённое оформление, расположение дорожек).
- Медицина (мониторы для наблюдения за сердечным ритмом).
- Метод освоения каллиграфических навыков в китайском языке.
Изучение этой темы в математике является обязательным, так как от этого зависит качество усвоения материала учеником.
Основные разновидности ломаных
Геометрическая фигура может быть построена совершенно по любому из действующих методов. Специалисты выделяют замкнутую, а также незамкнутую ломанную. Повышенное внимание уделяют самопересекающимся, непересекающимся линиям. Классическая замкнутая ломаная является многоугольником. В математике самопересекающейся принято называть ту линию, отрезки которой имеют минимум одно пересечение. По своей структуре ломаная может быть весьма разнообразной, из-за чего нужно внимательно относиться ко всем аспектам.
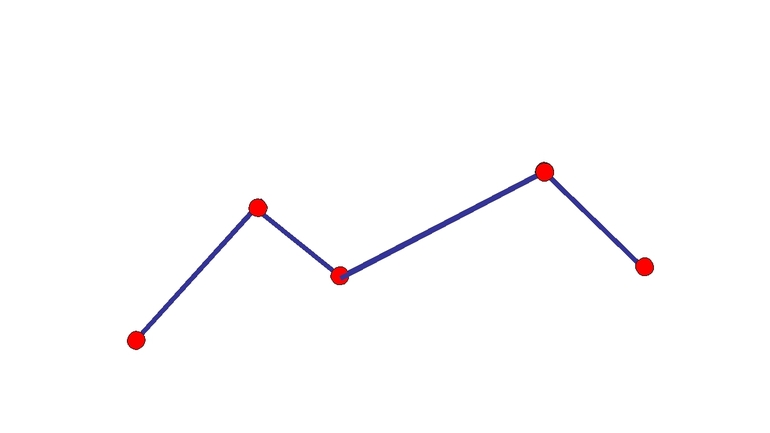
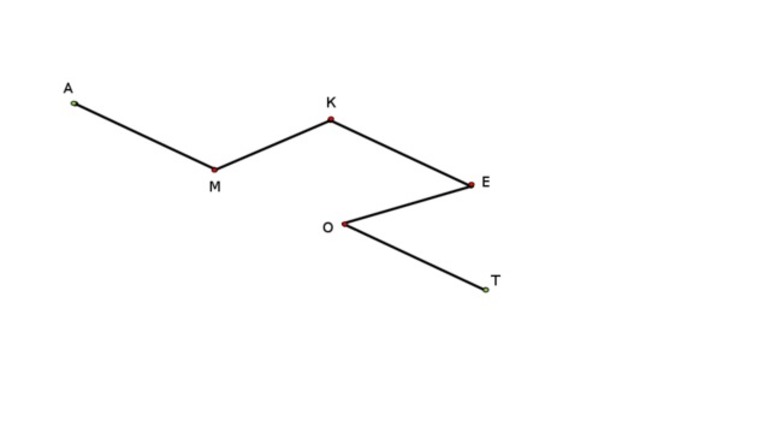
В начальных классах школы принято рассматривать следующий пример: ломаная включает в себя сразу пять звеньев либо сторон: ZX, XC, CV, VB, BN. Та точка, где неизбежно соединяются два звена, называется вершиной. В этом случае имеется сразу четыре вершины: X, С, V, B.
Повышенное внимание нужно уделить изучению звена ломаной. Звеньями эксперты привыкли называть стороны либо отрезки, из которых образована линия. Всего одно такое звено может быть рассмотрено только в качестве отрезка. А вот для построения ломаной необходимо задействовать как минимум два звена. Вершины — это классические точки, которые представляют собой концы одних отрезков ломаной. Обозначить точки можно только латинскими буквами.
Пример замкнутой, а также традиционной незамкнутой ломаной линии, которую часто можно встретить в геометрии и алгебре:
Если необходимо определить точную длину ломаной, то для этого следует поочерёдно сложить все известные данные задействованных звеньев (ZX + XC + CV + VB + BN).
Базовые понятия
Чтобы гарантировано освоить все правила, которые касаются использования изогнутой линии в математике, необходимо разобраться со звеньями. Существует ряд нюансов, которые можно сопоставить с элементарной геометрической конструкцией. Линию формируют отдельные отрезки, которые в математике называются звеньями. Если все концы ломаной соединяются в одной точке, то такая фигура будет называться замкнутой.
Все задействованные звенья могут обладать взаимными пересечениями. Вершинами специалисты привыкли называть точки соединения отрезков. О многоугольнике можно говорить только в том случае, если звенья не пересекаются между собой. Звено обозначают сразу двумя латинскими буквами. Каждая вершина изогнутой линии может обозначаться только одной буквой. Только тщательное изучение всех правил и нюансов позволит правильно решать математические задачи.
Особенности построения многоугольников
В этом случае речь касается геометрической фигуры, отличающейся итоговым количеством звеньев, углов. Последние могут быть сформированы только несколькими звеньями замкнутой ломаной, которые сходятся в одной точке. Задействованные звенья также могут носить логическое название сторон многоугольника. Общие точки двух отрезков называются вершинами. Стоит учесть, что количество сторон либо звеньев в каждой такой фигуре в точности соответствует количеству углов. Если задействовать замкнутую ломаную из трёх отрезков, то в итоге получится треугольник.
Абсолютно все многоугольники обладают одинаковыми свойствами. Самая маленькая фигура включает в себя всего три стороны. Но расположенные в непосредственной близости треугольники могут формировать совершенно новые фигуры. Если имеющиеся вершины изучаемого многоугольника являются своеобразным дополнением одной стороны, то их всегда называют соседними.
Когда многоугольник был расположен относительно одной прямой в любой плоскости, то она называется выпуклой. А вот прямая может содержать в себе одну сторону фигуры и принадлежать полуплоскости. Если отрезок соединяет не соседние вершины, то он называется диагональю. Смежный внутренний угол при некоторой вершине называется внешним.
Следует отметить тот факт, что когда все имеющиеся углы и стороны многоугольника равны между собой, то речь касается правильных отрезков. Каждая геометрическая фигура обладает определёнными параметрами. Треугольниками в алгебре принято называть обычную плоскую фигуру, которая состоит из трёх точек, не расположенных на одной прямой. Для соединения используются обычные отрезки. Точки выступают в роли вершин треугольника. Такая фигура имеет всего три угла. Специалисты различают 6 разновидностей треугольников:
- Элементарные разносторонние. В этом случае каждая следующая сторона отличается своей длиной.
- Равносторонние. Абсолютно все стороны обладают идентичной длиной.
- Специфические остроугольные. Сформированные углы имеют острую форму.
- Универсальные равнобедренные. Сразу две стороны из трёх существующих обладают одинаковой длиной.
- Тупоугольные. Фигура обладает одним тупым углом.
- Традиционные прямоугольные. Нарисованная фигура должна иметь минимум один прямой угол.
Четырёхугольником называют ту конструкцию, которая обладает четырьмя сторонами и четырьмя сторонами. Использование таких геометрических фигур обладает определёнными нюансами.
Ключевые нюансы
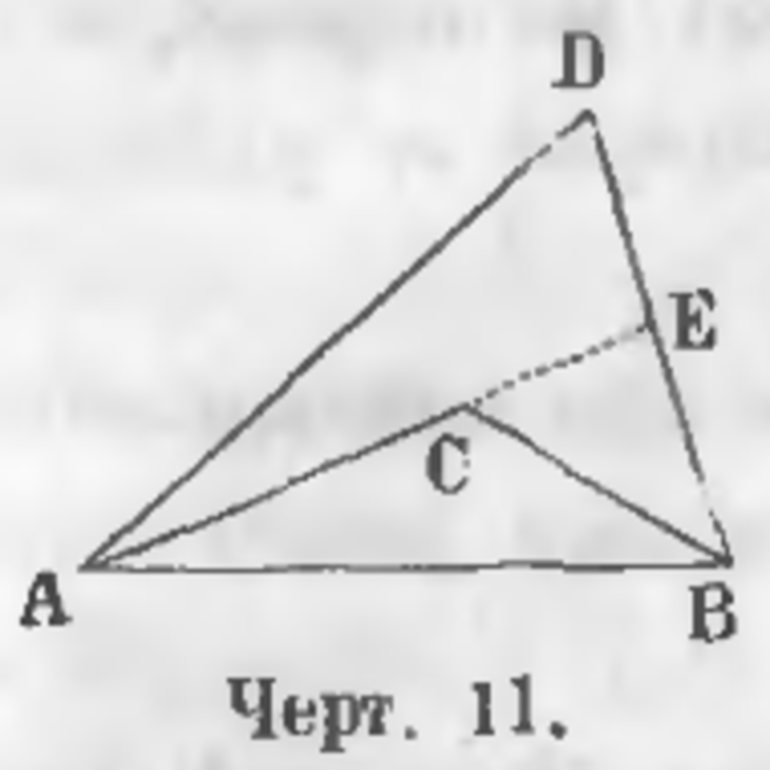
Существует две линии SWT и SFT одинаковой толщины, которые соединяют свободные концы одной прямой ST. В итоге образуется ломаная. Изогнутая SFT именуется внутренней ломаной, а вот SWT внешней. В качестве примера лучше всего рассмотреть фигуру, которая соответствует математической теореме, что внешняя изогнутая превышает внутреннюю.
По условиям задачи были даны две ломаные: внутренняя SFT и внешняя SWT. Необходимо доказать, что SWT больше SFT. Для решения этой задачи нужно продолжить линию SF до пересечения с отрезком WT в точке Е. Линия SWE как ломаная гораздо больше прямой SE. Ломанная FET больше имеющейся прямой FT. Если сложить между собой все эти неравенства, то в итоге можно получить: SW+ WE + FE + ET > SF + FE + FT.
Для получения достоверного результата нужно вычесть из обеих частей неравенства по СЕ:
- SW+ WE + ET > SF + FT.
- WE + ET = WT.
Необходимо рассмотреть и вторую теорему, в соответствии с которой итоговая сумма пересекающихся изогнутых линий больше не пересекающихся. По условиям задачи были даны обычные пересекающиеся ломаные HLK и HRK, а также HR, LK и пересекающиеся части. Решение выглядит следующим образом: неравенства отрезков вытекают из того, что ломаная HEL гораздо больше прямой HL, а вот координаты KER превышают KR.
Нелишним также будет научиться находить общую меру сразу двух линий при помощи линейки. Это правило обязательно осваивают в начальных классах. Для поиска неизвестной общей меры обязательно нужно на большую линию наложить меньшую, потом первый остаток на меньший отрезок, а второй остаток на первый. Все эти манипуляции повторяют ровно до тех пор, пока самый последний остаток максимально не уложится в предпоследнем выполненном действии. Измерение линий всегда означает то, что учащемуся необходимо отыскать её отношение к другим отрезкам, принятым за единицу. Полученное значение называют длиной этой линии, которая может выражаться исключительно в каких-нибудь единицах.
Изучение ломаных линий очень важно, так как они окружают человека повсюду. Речь касается прямых линий, которые меняют своё первоначальное направление, замыкаются, а также пересекаются.
http://izamorfix.ru/matematika/planimetriya/lomanaya.html
http://nauka.club/matematika/geometriya/loman%D0%B0y%D0%B0-lini%D1%83%D0%B0.html