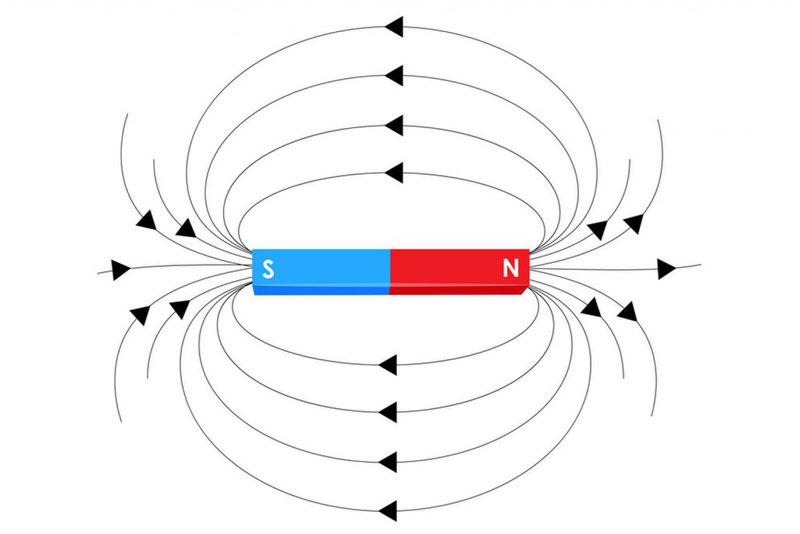
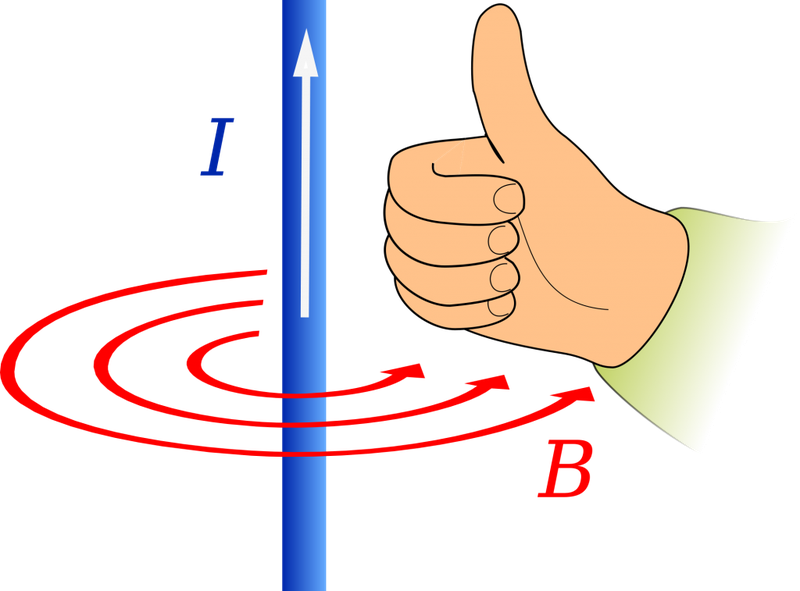
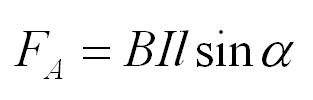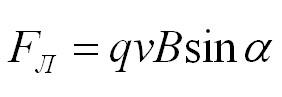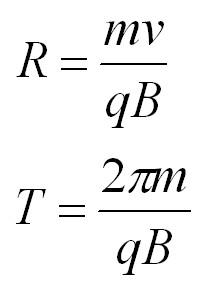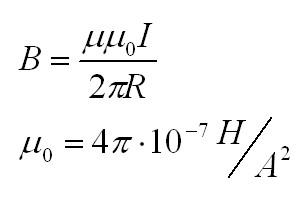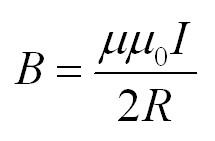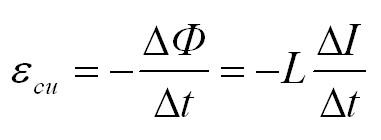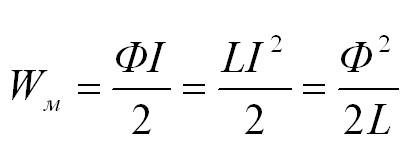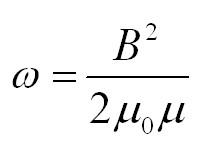Витал
Из формулы закона Ампера
Fa=B*I*L*sin a. ( Fa -сила Ампера, В -магнитная индукция, I -сила тока, L -длина, а (альфа) — угол между вектором магнитной индукции и проводником) выразим длину
L = Fa / B*I*sin a.
Общая информация о кабеле и проводе
При работе с проводниками необходимо понимать их обозначение. Существуют провода и кабеля, которые отличаются друг от друга внутренним устройством и техническими характеристиками. Однако многие люди часто путают эти понятия.
Проводом является проводник, имеющий в своей конструкции одну проволоку или группу проволок, сплетенных между собой, и тонкий общий изоляционный слой. Кабелем же называется жила или группа жил, имеющих как собственную изоляцию, так и общий изоляционный слой (оболочку).
Каждому из типов проводников будут соответствовать свои методы определения сечений, которые почти схожи.
Материалы проводников
Количество энергии, какую передает проводник, зависит от ряда факторов, главный из которых – это материал токопроводящих жил. Материалом жилок проводов и кабелей могут выступать следующие цветные металлы:
- Алюминий. Дешевые и легкие проводники, что является их преимуществом. Им присуще такие отрицательные качества, как низкая электропроводность, склонность к механическим повреждением, высокое переходное электросопротивление окисленных поверхностей;
- Медь. Наиболее популярные проводники, имеющие, по сравнению с другими вариантами, высокую стоимость. Однако им присуще малое электрическое и переходное на контактах сопротивление, достаточно высокая эластичность и прочность, легкость в спайке и сварке;
- Алюмомедь. Кабельные изделия с жилами из алюминия, которые покрыты медью. Им свойственна чуть меньшая электропроводность, чем у медных аналогов. Также им присуще легкость, среднее сопротивление при относительной дешевизне.
Важно! Некоторые способы определения сечения кабелей и проводов будут зависеть именно от материала их жильной составляющей, который напрямую влияет на пропускную мощность и силу тока (метод определения сечения жил по мощности и току).
Общие сведения
Упорядоченное движение носителей заряда в физическом теле называют электрическим током. Ими могут быть различные элементарные частицы. Например, в проводниках — электроны, электролитах — ионы. В состоянии покоя, то есть когда на тело не оказывается постороннее воздействие, движение носителей хаотичное. В результате происходит компенсирование зарядов, и ток не возникает. Если же к веществу приложить силу или деформировать его, направление движения частиц станет упорядоченным и возникнет электрический ток.
Все существующие вещества характеризуются физическими и химическими свойствами. Среди них и проводимость. Это электрическая величина, определяющая способность тела пропускать через себя ток. По своему строению все материалы делятся на 3 класса:
- проводники — вещества, не оказывающие сопротивление прохождению тока;
- полупроводники — тела, в которых величина проводимости зависит от чистоты материала, температуры и вида воздействующего излучения;
- диэлектрики — вещества, практически не проводящие электрический ток.
За единицу измерения силы тока принят Ампер, показывающий, какое количество электричества проходит через поперечное сечение проводника за одну секунду: I = q / t = кулон / секунду = ампер.
Электрическое сопротивление тела зависит от природы носителей заряда и геометрии материала. Это скалярный параметр. При его расчёте используют понятие удельное сопротивление. Выражают его в омах, умноженных на метр, и обозначают греческой буквой р. По физическому смыслу величина является обратным параметром удельной проводимости.
С ней, кроме сопротивления и силы тока, тесно связано и напряжение. С физической точки зрения, это работа, которую выполняет электрическое поле при переносе единичного заряда из одной точки в другую. В Международной системе величин напряжение принято обозначать в вольтах: U = f2- f1, где f — значения потенциала заряда в точках.
Для чего необходим расчет кабеля
В вопросе выбора сечения проводов нельзя следовать принципу «на глаз». Протекая по проводам, ток нагревает их. Чем выше сила тока, тем сильнее происходит нагрев. Эту взаимосвязь легко доказать парой формул. Первая из них определяет активную силу тока:
где I – сила тока, U – напряжение, R – сопротивление.
Из формулы видно: чем больше сопротивление, тем больше будет выделяться тепла, т. е. тем сильнее проводник будет нагреваться. Сопротивление определяют по формуле:
R = ρ · L/S (2),
где ρ – удельное сопротивление, L – длина проводника, S – площадь его поперечного сечения.
Чем меньше площадь поперечного сечения проводника, тем выше его сопротивление, а значит выше и активная мощность, которая говорит о более сильном нагреве. Исходя из этого, расчет сечения необходим для обеспечения безопасности и надежности проводки, а также грамотного распределения финансов.
Что будет, если неправильно рассчитать сечение
Без расчета сечения проводника можно столкнуться с одной из двух ситуаций:
- Слишком сильный перегрев проводки. Возникает при недостаточном диаметре проводника. Создает благоприятные условия для самовозгорания и коротких замыканий.
- Неоправданные затраты на проводку. Такое происходит в ситуациях, когда были выбраны проводники избыточного диаметра. Конечно, опасности здесь нет, но кабель большего сечения стоит дороже и не столь удобен в работе.
Что еще влияет на нагрев проводов
Из формулы (2) видно, что сопротивление проводника зависит не только от площади поперечного сечения. В связи с этим на его нагрев будут влиять:
- Материал. Пример – у алюминия удельное сопротивление больше, чем у меди, поэтому при одинаковом сечении проводов медь будет нагреваться меньше.
- Длина. Слишком длинный проводник приводит к большим потерям напряжения, что вызывает дополнительный нагрев. При превышении потерь уровня 5% приходится увеличивать сечение.
Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно
Вам это будет интересно Особенности индуктивного сопротивления
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Необходимость и порядок проведения расчета
Электрическим током питается самое разное оборудование, обладающее различной мощностью. И диапазон мощностей весьма обширный.
Каждый отдельно взятый электрический аппарат представляет собой нагрузку, в зависимости от величины которой требуется подвод тока определенной силы.
Необходимое количество тока под требуемую нагрузку можно пропустить через провода разного диаметра (сечения).
Но в условиях недостаточного сечения проводника для прохождения заданного объёма тока возникает эффект увеличенного сопротивления. Как следствие – отмечается нагрев провода (кабеля).
Если игнорировать подобное явление и продолжать пропускать ток, создаётся реальная опасность нагрева вплоть до момента возгорания. Такая ситуация грозит серьёзной аварийной ситуацией. Вот почему расчетам и подбору цепей передачи тока к нагрузке требуется уделять повышенное внимание.
Правильный расчёт, грамотный подбор кабелей и проводов положительно сказывается и на работе оборудования, выступающего в качестве нагрузки.
Так что, помимо фактора безопасности, расчёт сечений электрического кабеля по диаметру или наоборот, является обязательным действием с точки зрения обеспечения эффективной эксплуатации электрических машин.
Параллельное соединение проводов электропроводки
Бывают безвыходные ситуации, когда срочно нужно проложить проводку, а провода требуемого сечения в наличии нет. В таком случае, если есть провод меньшего, чем необходимо, сечения, то можно проводку сделать из двух и более проводов, соединив их параллельно. Главное, чтобы сумма сечений каждого из них была не меньше расчетной.
Например, есть три провода сечением 2, 3 и 5 мм2, а нужен по расчетам 10 мм2. Соединяете их все параллельно, и проводка будет выдерживать ток до 50 ампер. Да Вы и сами многократно видели параллельное соединение большего количества тонких проводников для передачи больших токов.
Например, для сварки используется ток до 150 А и для того, чтобы сварщик мог управлять электродом, нужен гибкий провод. Его и делают из сотен параллельно соединенных тонких медных проволочек. В автомобиле аккумулятор к бортовой сети тоже подключают с помощью такого же гибкого многожильного провода, так как во время пуска двигателя стартер потребляет от аккумулятора ток до 100 А.
А при установке и снятии аккумулятора необходимо провода отводить в сторону, то есть провод должен быть достаточно гибким. Способ увеличения сечения электропровода путем параллельного соединения нескольких проводов разного диаметра можно использовать только в крайнем случае. При прокладке домашней электропроводки допустимо соединять параллельно только провода одинакового сечения, взятые из одной бухты.
Способы измерения диаметра провода
Для того, чтобы рассчитать площадь поперечного сечения проводника необходимо знать его точный диаметр. Существует несколько способов измерения диаметра провода. К ним относятся измерения:
- При помощи штангенциркуля: для этого нужно понимать принцип работы штангенциркуля и уметь снимать показания с его шкал. В этом случае упростить измерения позволяет использование электронного измерительного прибора – он покажет точное значение диаметра на своем экране.
- С использованием микрометра: показания данного прибора немного точнее, чем у механического штангенциркуля, но он также требует некоторых навыков для снятия правильных и точных показаний.
- С помощью обычной линейки: данный способ подходит тем, кто не имеет в своем арсенале таких измерительных приборов, как штангенциркуль или микрометр. Измерение диаметра проводника с использованием линейки не будет достаточно точным, но примерно оценить диаметр будет возможно.
Для измерения диаметра проводника в первую очередь его зачищают ножом или стриппером от изоляции. Далее, если используется микрометр или штангенциркуль, жилу провода плотно зажимают между губок прибора и определяют размер проводника по шкалам устройства. При использовании линейки изоляция снимается на расстояние 5-10 см и жила наматывается на отвертку. Витки проводника должны плотно прижиматься друг к другу (ориентировочно 8-20 витков). Далее измеряется длина намотанного участка и полученное значение делится на количество витков – получится более или менее точное значение диаметра.
Определение диаметра жилы проводника
Собственно, выполнить эту операцию можно простым линейным замером. Для точного замера рекомендуется использовать точечный инструмент, например, штангенциркуль, а ещё лучше – микрометр.
Относительно низкий по точности результат, но вполне приемлемый для многих вариантов применения проводов даёт замер диаметра обычной линейкой.
Конечно же, измерение следует проводить в состоянии оголенного проводника, то есть предварительно снимается изоляционное покрытие.
Кстати, изоляционным покрытием, к примеру, медного провода, считается также тонкий слой напыления лака, которое также необходимо снимать, когда требуется очень точный расчет.
Существует «бытовой» способ измерения диаметра, пригодный в тех случаях, когда под руками отсутствуют точечные измерительные инструменты. Для применения способа потребуется отвертка электрика и школьная линейка.
Проводник под измерение предварительно зачищается от изоляции, после чего наматывается плотно виток к витку на штанге отвертки. Обычно мотают десяток витков – удобное число для математических расчетов.
Далее намотанную на штанге отвертки катушку измеряют линейкой от первого до последнего витка. Полученное значение на линейке необходимо разделить на число витков. Результатом такого нехитрого расчета будет диаметр жилы провода.
Вычисление сечения электрического провода
Для определения значения сечения жилы проводника придется уже пользоваться математической формулировкой.
По сути, сечением жилы проводника является площадь поперечного среза – то есть, площадь круга. Диаметр которого определяется методикой, описанной выше.
Опираясь на значение диаметра, несложно получить значение радиуса, разделив диаметр пополам.
Собственно, потребуется к полученным данным добавить константу «π» (3,14), после чего можно вычислить значение сечения по одной из формул:
S = π*R2 или S = π/4*D2,
где:
- D – диаметр;
- R – радиус;
- S – поперечное сечение;
- π – константа, соответствующая 3,14.
Указанные классические формулы используются и для определения сечения многожильных проводников. Стратегия расчёта остается практически неизменной, за исключением некоторых деталей.
В частности, изначально вычисляется сечение одной жилы из пучка, после чего полученный результат умножается на общее количество жил.
Рассчитать сечение многожильного проводника допустимо при помощи того же математического способа, что применяется к одинарному проводу, но дополнительно учитывается число существующих жил в качестве множителя
Почему следует считать важным фактором определение сечения? Очевидный момент, связанный напрямую законом Джоуля-Ленца, – потому что параметром сечения проводника определяется граница допустимого тока, текущего через этот проводник.
Определение диаметра по сечению
Математическим расчетом допустимо определить диаметр жилы проводника, когда известен параметр сечения.
Это, конечно, не самый практичный вариант, учитывая наличие более простых способов определения диаметра, но использование такого варианта не исключается.
Измерение диаметра с высокой точностью при помощи слесарного инструмента – микрометра, даёт практически аналогичный результат, когда расчеты проводят с помощью формулы
Для выполнения расчета потребуются фактически те же самые числовые сведения, что использовались при расчетах сечения с помощью математической формулы.
То есть, константа «π» и значение площади круга (сечения).
Применяя эти значения формулы ниже, получают значение диаметра:
D = √4S/π,
где:
- D – диаметр;
- S – поперечное сечение;
- π – константа, соответствующая 3,14.
Применение этой формулы может быть актуальным, когда известен параметр сечения и под руками нет никаких подходящих инструментов для измерения диаметра.
Параметр сечения допустимо получить, к примеру, из документации на проводник или из таблицы для расчетов, где представлены наиболее часто используемые классические варианты.
Определяем сечение провода с помощью таблицы
Использование формул не дает гарантированного результата, да и как назло они забываются в самый нужный момент. Поэтому определение сечения лучше проводить согласно таблице, куда сведены результаты вычислений. Если получилось измерить диаметр жилы, то площадь сечения провода можно посмотреть в соответствующем столбце таблицы:
Если надо найти общий диаметр многопроволочной жилы кабеля, то придется отдельно вычислить диаметр каждого проводка, а полученные значения сложить. Дальше все делается так же, как и с однопроволочной жилой – результат находится по формуле или таблице.
При замерах сечения провода, его жила тщательно очищается от изоляции, так как не исключена возможность что ее толщина будет больше нормативной. Если в точности расчетов по каким-либо причинам есть сомнения, то лучше выбирать кабеля или провода с запасом мощности.
Чтобы приблизительно узнать сечение провода, который будет приобретаться, надо сложить мощности электрооборудования, что будет к нему подключено. Потребляемая мощность обязательно указывается в паспорте прибора. По известной мощности высчитывается суммарный ток, который будет протекать по проводнику, а исходя из него уже подбирается сечение.
Особенности электрических проводов
Наиболее широкое применение находят марки проводов ПУHП и ПУГHП, а также ВПП, ПHCB и PKГM, которые обладают следующими, очень важными для получения безопасного подключения основными техническими характеристиками:
- ПУНП — плоское проводное изделие установочного или так называемого монтажного типа, с однопроволочными жилами из меди в ПВХ-изоляции. Такая разновидность отличается количеством жил, а также номинальным напряжением в пределах 250 В с частотой 50 Гц и температурным эксплуатационным режимом от минус 15 °C до плюс 50 °C;
- ПУГНП — гибкая разновидность с многопроволочными жилами. Основные показатели, которые представлены номинальным уровнем напряжения, частотой и температурным эксплуатационным режимом, не отличаются от аналогичных данных ПУHП;
- AПB — алюминиевая одножильная разновидность, круглый провод, имеющий защитную ПВХ-изоляцию и однопроволочную или многопроволочную жилу. Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
- ПBC — многожильная медная разновидность с ПBX-изоляцией, придающей проводу высокие показатели плотности и традиционную округлую форму. Термоустойчивая жила рассчитана для номинального уровня 380 В при частоте 50 Гц;
- PKГM — силовая монтажная разновидность, представленная одножильным медным проводом с кремнийорганической резиновой или стекловолоконной изоляцией, пропитанной термостойким составом. Температурный эксплуатационный режим составляет от минус 60 °C до плюс 180 °C;
- ПHCB — нагревательная одножильная разновидность в виде однопроволочного провода на основе оцинкованной или вороненой стали. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 80 °C;
- ВПП — одножильная медная разновидность с многопроволочной жилой и изоляцией на основе ПBX или полиэтилена. Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
В условиях невысокой мощности применяется медный провод ШBBП с защитной внешней ПBX-изоляцией. Многопроволочного типа жила обладает прекрасными показателями гибкости, а само проводное изделие рассчитано максимум на 380 В, при частоте в пределах 50 Гц.
Проводные изделия самых распространенных типов реализуются в бухтах, и чаще всего имеют белое окрашивание изоляции.
Детальная инструкция по проведению замеров
Весь процесс вычисления параметров сечения кабеля можно разделить на 6 этапов, каждый из которых имеет свою специфику и должен подчиняться конкретным правилам.
1 этап
Нужно взять кабель, для которого человек собирается определять параметр сечения. Чаще всего для такой цели используются провода, состоящие из 2 или 4 жил. Жилы должны быть изолированы друг от друга специальными материалами.
Как правило, жилы внутри кабеля обладают одинаковыми показателями диаметра, но можно и встретить такие варианты провода, где одна из жил намного тоньше остальных вариантов. Если в кабеле есть одна тонкая жила, значит, она предназначается для заземления.
2 этап
Жилы необходимо очень аккуратно очистить от изоляции провода – с этой целью нужно использовать небольшой, но очень острый нож.
Затем взять штангенциркуль или микрометр и, воспользовавшись инструментом, рассчитать диаметр жилы. Полученное в миллиметрах значение стоит куда-то записать. Используя этот параметр, нужно будет рассчитать такой показатель, как площадь поперечного сечения. Чтобы это сделать, человеку придется умножить коэффициент 0,25 на число П, которое ровняется 3,14, а также на полученное значение диаметра в квадрате. Общая формула для этого расчета выглядит так – S=0,25xПxD в квадрате. Полученное значение необходимо умножить на количество жил, которые присутствуют в определенном кабеле.
Дополнительно нужно вычислить сопротивление провода, для чего понадобятся следующие показатели:
- длина провода;
- сечение кабеля;
- материал, из которого изготовлен кабель.
Имея эти параметры, можно без проблем вычислить показатель сопротивления.
3 этап
Чтобы понять, как делаются замеры на практике и узнать нужную информацию, нужно рассмотреть момент расчета на конкретном примере. Если у пользователя в руках есть медный кабель, который состоит из 4 жил, а параметр его диаметра составляет 2мм, то можно искать площадь его сечения.
Совет! Для проведения замеров лучше использовать микрометр, который позволит получить более точные показатели, а значит, и весь расчет будет максимально точным и правильным.
Чтобы определить этот параметр, стоит заняться моментом расчета площади поперечного сечения для одной из жил. Сделать это позволяет следующая формула:
S=0,25х3,14х2 в квадрате = 3,14мм в квадрате
4 этап
Определив параметр сечения, человек может узнать, какой максимальный ток может протекать именно по выбранному кабелю. Также, имея выше указанный показатель на руках, человек может определить сопротивление. К примеру, максимальный ток именно для кабеля из меди можно рассчитать, используя соотношение 8А на 1мм в квадрате. Исходя из этого, предельное значение тока будет составлять 8х12,56=100,5А. для алюминиевого кабеля используются немного другие параметры, которые составляют 5А на 1мм квадратный.
5 этап
Зная значение длины кабеля, можно легко опередить его сопротивление. Чтобы понять, как это делается, нужно рассмотреть все на конкретном примере. К примеру, если длина конкретного кабеля составляет 200м, то чтобы определить показатель сопротивления, нужно умножить удельное сопротивление материала на длину кабеля и поделить на площадь его поперечного сечения. Сделав эти расчеты, можно без проблем определить нужный параметр.
Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера
Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
Анализ задачи:
Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.
Решение:
Определим направление силы Ампера, действующая на проводник А, находящегося в магнитном поле проводника В.
1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (о).
2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.
3) Приходим к выводу: проводник А привлекается к проводнику В.
Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (о).
2) Определим направление силы Ампера, действующая на проводник В.
3) Приходим к выводу: проводник В привлекается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.
Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?
Анализ задачи:
Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:
- сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх)
- значение силы Ампера равна значению силы тяжести FA = Fтяж
Направление тока определим, воспользовавшись правилом левой руки.
Решение:
Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.
Учитываем, что FA = Fтяж. FA= BIlsinα, где sin α = 1; Fтяж = mg
Из последнего выражения найдем силу тока: I = mg/Bl
Проверим единицу, найдем значение искомой величины.
Подводим итоги
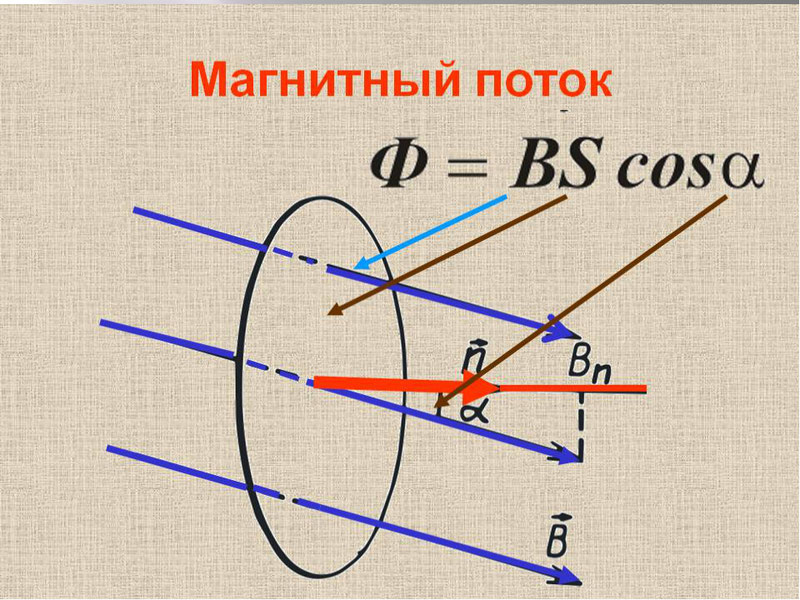
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: FA= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.
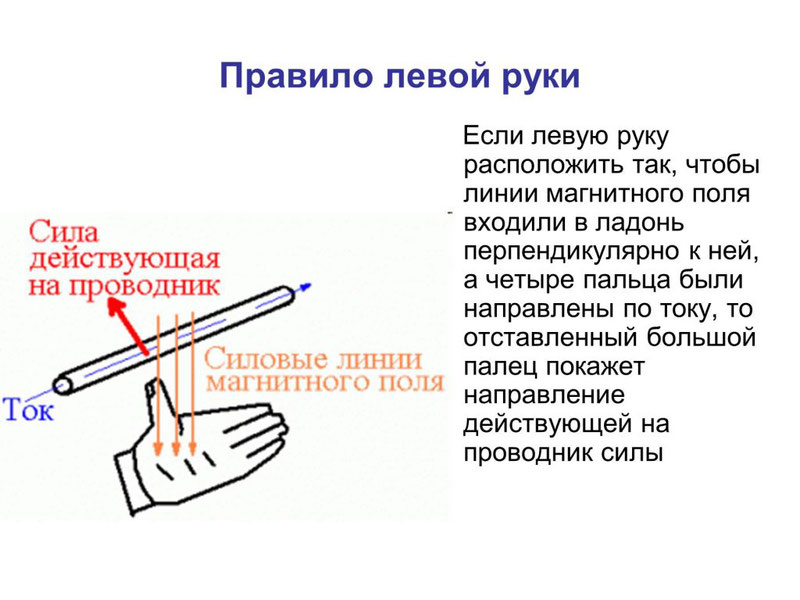
Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.
Определение сечения провода на примере
Для определения площади поперечного сечения жилы провода или кабеля, используют штангенциркуль с обычной шкалой либо циферблатный или цифровой прибор. Как определить сечение провода штангенциркулем? Для опытных электриков данный вопрос может показаться смешным, а обычного домашнего мастера этот вопрос может загнать в тупик. Рассмотрим измерение провода на примере.
В первую очередь освежим память школьного курса геометрии, а именно вспомним формулу определения площади круга:
Sкр=πr2 ,
где π=3,14; r – радиус окружности.
Приведем данную формулу для нашего случая, а также немного упростим ее. Штангенциркулем измеряют не радиус, а диаметр круга. Исходя из того, что радиус это половина диаметра, получаем следующую формулу:
Sкр=(πd2)/4 ,
где d – диаметр окружности, в данном случае жилы.
Для удобства расчета упростим формулу, разделив π на четыре, получаем:
Sкр=0,785d2
Из полученного выражения видно, что для определения площади поперечного сечения необходимо знать диаметр провода. Итак, берем провод, очищаем жилу, сечение которой хотим определить. Затем измеряем диаметр жилы штангенциркулем.
Получаем 1,78 мм. Подставляем полученное значение в формулу: 1,78 возводим в квадрат и умножаем на 0,785, округляем до сотых, получаем 2,49 – сечение провода.
Как правило, не у каждого домашнего электрика есть в хозяйстве штангенциркуль. Покупать его для измерения на несколько раз, в процессе замены электропроводки не целесообразно. Как определить сечение провода, не имея штангенциркуля? Оказывается очень просто: существует еще один способ измерения сечения жилы, который сможет выполнить любой человек, имея под рукой карандаш и линейку.
Берем провод, сечение которого нам необходимо узнать, и зачищаем его на длину около 30-50 сантиметров. Затем берем карандаш (ручку, фломастер и т.п.) и наматываем на него провод таким образом, чтобы витки наматываемого провода были вплотную друг другу.
Теперь подсчитываем количество намотанных на карандаш витков и измеряем их общую длину, в данном случае их 19, длинна – 32 миллиметров. Для определения диаметра одного витка необходимо общую их длину разделить на количество витков: 32 делим на 19 получаем 1,684 миллиметра. Подставляем диаметр в формулу, как и в предыдущем измерении, получаем 2,23 квадратных миллиметров. Провод для примера был взят из кабеля ВВГнг-2,5×7.
Если в хозяйстве есть провод и вы хотите его использовать для прокладки проводки, то можно определить сечение таким простым способом, сэкономив деньги на приобретение специального измерительного прибора, который, насколько мне известно, стоит сравнительно большую сумму.
Насколько точный результат предложенного выше метода? Все зависит от количества витков, чем их больше, тем меньше погрешность в результате. Единственный минус данного метода – достаточно большое сечение жилы измерить не получится. Представьте можно ли намотать провод сечением в 6 квадратов на карандаш или что-то подобное? В этом случае без специального устройства не обойтись.
Для определения сечения провода для проводки квартиры вышеуказанного способа достаточно. Приобретение штангенциркуля будет необходимо в том случае, если вы занимаетесь монтажом электропроводки профессионально. Наматывать провод каждый раз на карандаш будет очень долгим занятием. А вообще, как говорится, все приходит с опытом: бывалый электрик, проложивший не один километр провода, вмиг определит сечение провода без помощи каких-либо методов.
Существуют также специальные таблицы, которые несколько упрощают расчеты. В них приведены номинальные сечения проводов и соответствующие им диаметры для различных типов проводов, как одножильных, так и многожильных (гибких).
Зависимость тока, мощности и сечения жил
Измерить и произвести расчеты площади сечения кабеля по диаметру жилы недостаточно. Перед прокладкой проводки или иных типов электросетей необходимо также знать пропускную способность кабельной продукции.
- Выбирая кабель, необходимо руководствоваться несколькими критериями:
- сила электротока, которую будет пропускать кабель;
- мощность потребителей;
- токовая нагрузка, оказываемая на кабель.
Мощность
Самым важным параметром при электромонтажных работах (в частности прокладке кабелей) является пропускная мощность. От сечения проводника зависит максимальная мощность передаваемой по нему электроэнергии
Поэтому крайне важно знать общую мощность источников потребления энергии, которые будут подключены к проводу
Обычно производители бытовой техники, приборов и иных электротехнических изделий указывают на этикетке и в прилагаемой к ним документации максимальную и среднюю мощность потребления.
Например, машина для стирки белья может потреблять электроэнергию в диапазоне от десятков Вт/ч при режиме полоскания до 2,7 кВт/ч при нагреве воды.
Соответственно, к ней должен подключаться провод с тем сечением, которого хватит для передачи электроэнергии максимальной мощности. Если к кабелю подключается два и более потребителя, то общая мощность определяется путем сложения предельных значений каждого из них.
Усредненная мощность всех электроприборов и осветительных устройств в квартире редко превышает 7500 Вт для однофазной сети. Соответственно, сечения кабелей в электропроводке необходимо подбирать под это значение.
Рекомендуется округлять сечение в сторону увеличения мощности из-за возможного увеличения потребляемой электроэнергии в будущем. Обычно берут следующую по числу площадь сечения от рассчитанной величины. Так, для значения общей мощности 7,5 кВт необходимо использовать медный кабель с сечением жилы 4 мм2, который способен пропустить около 8,3 кВт. Сечение проводника с алюминиевой жилой в таком случае должно быть не менее 6 мм2, пропускающее мощность тока от 7,9 кВт.
В индивидуальных жилых постройках нередко применяется трехфазная система электроснабжения на 380 В. Однако большая часть техники не рассчитана на такое электронапряжение. Напряжение в 220 В создается посредством их подсоединения в сеть через нулевой кабель с равномерным распределением токовой нагрузки на все фазы.
Электроток
Зачастую мощность электрооборудования и техники может быть не известна владельцу из-за отсутствия этой характеристики в документации или полностью утерянных документов, этикеток. Выход в такой ситуации один – произвести расчет по формуле самостоятельно.
Мощность определяется по формуле:
P = U*I
- где:
- Р – мощность, измеряемая в ваттах (Вт);
- I – сила электротока, измеряемая в амперах (А);
- U – приложенное электронапряжение, измеряемое в вольтах (В).
- Когда неизвестна сила электротока, то ее можно измерить контрольно-измерительными приборами:
- амперметром;
- мультиметром;
- токоизмерительными клещами.
После определения потребляемой мощности и силы электротока можно посредством нижеприведенной таблицы узнать необходимое сечение кабеля.
Нагрузка
Расчет сечения кабельных изделий по токовой нагрузке необходимо производить для дальнейшей защиты их от перегрева. Когда по проводникам проходит слишком большой электроток для их сечения, то может происходить разрушение и оплавление изоляционного слоя.
Предельно допустимая длительная токовая нагрузка – это количественное значение электротока, который сможет пропускать кабель достаточно долго без перегревов. Для определения этого показателя изначально необходимо просуммировать мощности всех энергопотребителей.
После этого произвести вычисления токовой нагрузки по формулам:
однофазная сеть: I = P∑*Ki/U
трехфазная сеть: I = P∑*Ki/(√3*U)
- где:
- P∑ – общая мощность энергопотребителей;
- Ki – коэффициент, равный 0,75;
- U – электронапряжение в сети.
Советы по выбору сечения провода
Сечение проводника – это не все, на что нужно обращать внимание. Немаловажное значение имеет материал, из которого он изготовлен. Жила из меди или алюминия имеет определенный цвет и если он вызывает сомнение, то вероятно в целях экономии здесь производителем используется сплав металла. Это может привести к опасным последствиям, так как проводимость тока будет меньше, чем у заявленных металлов.
Сечение провода определяется только по диаметру токоведущей жилы. Некоторые покупатели ошибочно пытаются вычислить сечение по общему диаметру (жила+изоляция), отнимая от результата предполагаемую толщину изоляции. Так делать ни в коем случае нельзя, так как погрешность измерения будет чрезмерно высокой. Кроме того, в целях экономии металла производителем может быть сделана толще сама изоляция, и на вид изделие кажется вполне нормальным.
Источники
- https://www.boncom.by/papers/raschet-secheniya-kabelya
- https://amperof.ru/elektromontazh/electroprivodka/tablitsa-diametr-sechenie-provoda.html
- https://sovet-ingenera.com/elektrika/wires/sechenie-provoda-po-diametru.html
- https://odinelectric.ru/wiring/wires/opredelenie-ploshhadi-sechenija-provodnika-po-ego-diametru
- https://YaElectrik.ru/elektroprovodka/kak-opredelit-sechenie-provoda
- https://enargys.ru/kak-opredelit-sechenie-kabelya-po-diametru/
- https://elektri4estwo.ru/elektrika-v-kvartire/41-kak-opredelit-sechenie-provoda.html
[свернуть]
Похожие записи:
- Расчет сечения кабеля по мощности: формулы, таблицы,…
- Какой кабель использовать для проводки в квартире и…
- Особенности составления схемы проводки в дачном…
- Розетка для духового шкафа: какая нужна розетка для…
- Как найти скрытую проводку в стене: способы на выбор
- Электропроводка в деревянном доме своими руками
Расчет длины электрического проводника
Длину электрического проводника рассчитываем по формуле:
L = R * S / ρ
- L — длина электрического проводника
- R — сопротивление электрического проводника
- S — сечение электрического проводника
- ρ — удельное сопротивление проводника вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)] ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Как правильно выбрать сечение кабеля заземления?
Перед тем как выбирать размер сечения проводки, нужно определиться с типом защитной системы.
Похожее: Как выбрать диаметр подрозетника
Согласно ПЭУ, приняты к использованию следующие варианты:
- нейтральный кабель подключается к заземлителю при использовании переменного тока;
- объединение нулевого кабеля и «земли» вместе, нейтральная проводка подсоединяется отдельно;
- подсоединение электрооборудования напрямую к главной заземляющей шине;
- создание заземления на корпусе электрического устройства с помощью сопротивления или путем изоляции всех кабелей.
При выборе кабеля нужно ориентироваться на маркировку, в которой РЕ обозначает «заземление», а «земля» и «ноль» обозначаются маркировкой PEN при соединении в одном проводе.
При подборе размера сечения проводов необходимо учитывать тип самого заземления, которое может быть переносным или стационарным. В быту обычно используется стационарный тип защитного устройства. При такой схеме приборы к заземляющему проводнику могут подсоединяться многожильными и одножильными кабелями. Выбирая подходящие проводящие жилы при создании защитных систем нужно использовать рекомендованные размеры диаметра используемой проводки.
Допустимые токи нагрузки медных проводов (монтажных)
| Параметр | Сечение провода, мм 2 | ||||||||||||||
| 0,05 | 0,07 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,7 | 1 | 1,5 | 2 | 2,5 | 4 | 6 | 11 | |
| Наибольший допустимый ток, А | 0,7 | 1 | 1,3 | 2,5 | 3,5 | 4 | 5 | 7 | 10 | 14 | 17 | 20 | 25 | 30 | 54 |
- В.Г.Бастанов. 300 практических советов. Московский рабочий, 1986.
Оглавление
На чтение 21 мин. Просмотров 97 Опубликовано 19.02.2021
Содержание
- 1 Зависимость тока, мощности и сечения жил
- 2 Особенности электрических проводов
- 3 Особенности электрических проводов
- 4 Как найти длину проводника
- 5 Расчет резисторов
- 6 Параллельное соединение проводов электропроводки
- 7 Как найти с помощью формулы напряжение
- 8 Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера
- 9 Достоинства и недостатки медных проводов
- 10 Как определить сечение кабеля по диаметру, формула, таблица
- 11 Общие сведения
Зависимость тока, мощности и сечения жил
Измерить и произвести расчеты площади сечения кабеля по диаметру жилы недостаточно. Перед прокладкой проводки или иных типов электросетей необходимо также знать пропускную способность кабельной продукции.
- Выбирая кабель, необходимо руководствоваться несколькими критериями:
- сила электротока, которую будет пропускать кабель;
- мощность потребителей;
- токовая нагрузка, оказываемая на кабель.
Мощность
Самым важным параметром при электромонтажных работах (в частности прокладке кабелей) является пропускная мощность. От сечения проводника зависит максимальная мощность передаваемой по нему электроэнергии
Поэтому крайне важно знать общую мощность источников потребления энергии, которые будут подключены к проводу
Обычно производители бытовой техники, приборов и иных электротехнических изделий указывают на этикетке и в прилагаемой к ним документации максимальную и среднюю мощность потребления.
Например, машина для стирки белья может потреблять электроэнергию в диапазоне от десятков Вт/ч при режиме полоскания до 2,7 кВт/ч при нагреве воды.
Соответственно, к ней должен подключаться провод с тем сечением, которого хватит для передачи электроэнергии максимальной мощности. Если к кабелю подключается два и более потребителя, то общая мощность определяется путем сложения предельных значений каждого из них.
Усредненная мощность всех электроприборов и осветительных устройств в квартире редко превышает 7500 Вт для однофазной сети. Соответственно, сечения кабелей в электропроводке необходимо подбирать под это значение.
Рекомендуется округлять сечение в сторону увеличения мощности из-за возможного увеличения потребляемой электроэнергии в будущем. Обычно берут следующую по числу площадь сечения от рассчитанной величины. Так, для значения общей мощности 7,5 кВт необходимо использовать медный кабель с сечением жилы 4 мм2, который способен пропустить около 8,3 кВт. Сечение проводника с алюминиевой жилой в таком случае должно быть не менее 6 мм2, пропускающее мощность тока от 7,9 кВт.

В индивидуальных жилых постройках нередко применяется трехфазная система электроснабжения на 380 В. Однако большая часть техники не рассчитана на такое электронапряжение. Напряжение в 220 В создается посредством их подсоединения в сеть через нулевой кабель с равномерным распределением токовой нагрузки на все фазы.
Электроток
Зачастую мощность электрооборудования и техники может быть не известна владельцу из-за отсутствия этой характеристики в документации или полностью утерянных документов, этикеток. Выход в такой ситуации один – произвести расчет по формуле самостоятельно.
Мощность определяется по формуле:
P = U*I
- где:
- Р – мощность, измеряемая в ваттах (Вт);
- I – сила электротока, измеряемая в амперах (А);
- U – приложенное электронапряжение, измеряемое в вольтах (В).
- Когда неизвестна сила электротока, то ее можно измерить контрольно-измерительными приборами:
- амперметром;
- мультиметром;
- токоизмерительными клещами.
После определения потребляемой мощности и силы электротока можно посредством нижеприведенной таблицы узнать необходимое сечение кабеля.
Нагрузка
Расчет сечения кабельных изделий по токовой нагрузке необходимо производить для дальнейшей защиты их от перегрева. Когда по проводникам проходит слишком большой электроток для их сечения, то может происходить разрушение и оплавление изоляционного слоя.
Предельно допустимая длительная токовая нагрузка – это количественное значение электротока, который сможет пропускать кабель достаточно долго без перегревов. Для определения этого показателя изначально необходимо просуммировать мощности всех энергопотребителей.
После этого произвести вычисления токовой нагрузки по формулам:
однофазная сеть: I = P∑*Ki/U
трехфазная сеть: I = P∑*Ki/(√3*U)
- где:
- P∑ – общая мощность энергопотребителей;
- Ki – коэффициент, равный 0,75;
- U – электронапряжение в сети.
Особенности электрических проводов
При всём многообразии кабельной продукции и огромном выборе проводов для прокладки электрических сетей существуют правила подбора. Не обязательно учить наизусть все марки кабелей и проводов, нужно уметь читать и расшифровывать их маркировку. Для начала стоит выяснить различие между проводом и кабелем.
Провод – проводник, используемый для соединения двух участков цепи. Может иметь одну или несколько токопроводящих жил. Жилы могут быть:
Голые линии применяются там, где прикосновение к токоведущим жилам невозможно. В большинстве случаев они используются для воздушных линий электропередач.
Изоляционное покрытие применяется однослойное или двухслойное. Провода, имеющие два или три проводника в двойной изоляции, путают с кабелем. Путаница происходит из-за того, что изоляция покрывает каждую жилу, а снаружи выполнено общее полимерное или иное покрытие. Такие проводники нашли применение внутри электрических устройств, щитов или шкафов. В быту они скрыты в стене или проложены в специальных каналах.
Изолированная продукция используется повсеместно. В зависимости от степени электробезопасности помещения и места прокладки, выбирается класс изоляции.
Многожильные проводники используются там, где необходимы изгибы малого радиуса при прокладке сложных трасс, где не могут пройти одножильные аналоги. Такой тип тоководов удобно монтировать в кабельных каналах. Одножильные провода в таких условиях изгибать труднее, нужно прикладывать силу, и существует опасность повреждения жилы.
К сведению. Маркировка АППВ 3*2,5 обозначает провод с алюминиевыми жилами, поливинилхлоридной изоляцией, плоский, имеющий разделительное основание. Расшифровку маркировки уточняют в справочной литературе.
По строению кабель – это сколько-то жил, имеющих индивидуальную изоляцию, помещённых в защитный внешний слой из диэлектрического материала. Пространство между сердечниками и оболочкой, для предотвращения слипания, заполняется бумажными лентами, пластмассовыми нитями или кабельной пряжей. Дополнительно изделие может быть усилено бронёй из лент или стальной оплёткой для защиты от механических повреждений.
Особенности электрических проводов
Наиболее широкое применение находят марки проводов ПУHП и ПУГHП, а также ВПП, ПHCB и PKГM, которые обладают следующими, очень важными для получения безопасного подключения основными техническими характеристиками:
- ПУНП — плоское проводное изделие установочного или так называемого монтажного типа, с однопроволочными жилами из меди в ПВХ-изоляции. Такая разновидность отличается количеством жил, а также номинальным напряжением в пределах 250 В с частотой 50 Гц и температурным эксплуатационным режимом от минус 15 °C до плюс 50 °C;
- ПУГНП — гибкая разновидность с многопроволочными жилами. Основные показатели, которые представлены номинальным уровнем напряжения, частотой и температурным эксплуатационным режимом, не отличаются от аналогичных данных ПУHП;
- AПB — алюминиевая одножильная разновидность, круглый провод, имеющий защитную ПВХ-изоляцию и однопроволочную или многопроволочную жилу. Отличием данного вида является устойчивость к повреждениям механического типа, вибрациям и химическим соединениям. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 70 °C;
- ПBC — многожильная медная разновидность с ПBX-изоляцией, придающей проводу высокие показатели плотности и традиционную округлую форму. Термоустойчивая жила рассчитана для номинального уровня 380 В при частоте 50 Гц;
- PKГM — силовая монтажная разновидность, представленная одножильным медным проводом с кремнийорганической резиновой или стекловолоконной изоляцией, пропитанной термостойким составом. Температурный эксплуатационный режим составляет от минус 60 °C до плюс 180 °C;
- ПHCB — нагревательная одножильная разновидность в виде однопроволочного провода на основе оцинкованной или вороненой стали. Температурный эксплуатационный режим составляет от минус 50 °C до плюс 80 °C;
- ВПП — одножильная медная разновидность с многопроволочной жилой и изоляцией на основе ПBX или полиэтилена. Температурный эксплуатационный режим составляет от минус 40 °C до плюс 80 °C.
В условиях невысокой мощности применяется медный провод ШBBП с защитной внешней ПBX-изоляцией. Многопроволочного типа жила обладает прекрасными показателями гибкости, а само проводное изделие рассчитано максимум на 380 В, при частоте в пределах 50 Гц.
Проводные изделия самых распространенных типов реализуются в бухтах, и чаще всего имеют белое окрашивание изоляции.
Как найти длину проводника
Автор Ольга Громышева задал вопрос в разделе Естественные науки Какая формула нахождения длины проводника? и получил лучший ответ
Ответ от Крабочка а формула R=p*L /S. Вот и вычисляй отсюда L
Проверка на длительно допустимый ток и потерю напряжения подробнее.
Найти длину проводника очень просто – достаточно его измерить. Однако, если проводник недоступен или имеет очень большую длину, то его непосредственное измерение может оказаться весьма затруднительным.
— строительная рулетка; — амперметр (тестер); — штангенциркуль; — таблица электропроводности металлов.
Чтобы найти длину проводника, измерьте рулеткой длины его отдельных участков и сложите их. Этот метод подходит для открытой электропроводки и замеров провода во временных кабельных соединениях.
Если электропроводка скрытая, то для нахождения точной длины проводника воспользуйтесь соответствующей электромонтажной схемой. Если таковой схемы нет, то попробуйте косвенно восстановить размещение проводов по положению розеток, выключателей, распределительных коробок и т.п. признакам.
Учтите важное правило электромонтажников: все провода должны прокладываться строго горизонтально или вертикально. Причем, горизонтальные участки провода, как правило, проходят вдоль верхнего края стены (под потолком)
Однако, действительное расположение проводов сможет определить только специальный прибор или опытный электрик.
Если восстановить траекторию скрытой электропроводки невозможно, то измерьте электрическое сопротивление отдельных участков проводника. Для расчетов уточните также сечение проволоки и материал, из которого она состоит. Как правило, это – медь или алюминий. Так как формула для расчета сопротивления: R = ? * L * s, то длину проводника можно рассчитать по формуле:
где: L – длина проводника, R – сопротивление проводника, ? – удельное сопротивление материала из которого сделан проводник, s – площадь поперечного сечения проводника.
При расчете длины проводника учтите следующие параметры и соотношения.
Удельное сопротивление медного провода составляет 0,0154 — 0,0174 ом, алюминиевого: 0,0262 — 0,0278 ом. (Если длина проводника равна 1 метру, а сечение – 1 мм?).
Сечение проводника равняется:
где: ? — число «пи», приблизительно равное 3,14, D – диаметр проволоки (который легко замерить штангенциркулем).
Если провод смотан в катушку, то определите длину одного витка и умножьте на количество витков.
Если катушка имеет круглое сечение, то измерьте диаметр катушки (средний диаметр обмотки, если она многослойная). Затем умножьте диаметр на число «пи» и на количество витков:
d –диаметр катушки, n – количество витков провода.
Удельное сопротивление есть характеристика материала, вещества из которого сделан проводник.
Электрическое сопротивление проводника прямо пропорционально произведению удельного сопротивления материала из которого сделан проводник на его длинну, и обратно пропорционально его сечению.
| электрическое сопротивление проводника, | Ом |
| удельное сопротивление материала проводника, | Ом·м |
| длина проводника, | Метр |
| сечение проводника, | Метр2 |
Единица СИ удельного сопротивления
Удельное сопротивление ρ зависит от температуры.
Расчет резисторов
Для подбора и установки элементов в схему необходимо предварительно рассчитать номинал и мощность компонентов.
Формула для расчета сопротивления и мощности
Сопротивление тока: формула
Используют Закон Ома для участка цепи, чтобы вычислить сопротивление резистора, формула имеет вид:
R = U/I,
где:
- U – напряжение на выводах элемента, В;
- I – сила тока на участке цепи, А.
Эта формула применима для токов постоянного направления. В случае расчётов для переменного тока берут в расчёт импеданс цепи Rz.
Важно! Строение схем не ограничивается установкой только одного резистора. Обычно их множество, соединены они между собой параллельно и последовательно
Для нахождения общего показателя применяют отдельные методы и формулы.
Последовательное соединение
При таком соединении «выход» одного элемента соединяется с «входом» другого, они идут последовательно друг за другом. Как рассчитать резистор в этом случае? Можно использовать электронный онлайн-калькулятор, можно применить формулу.
Общее значение будет составлять сумму сопротивлений компонентов, входящих в последовательное соединение:
R123 = R1+R2+R3.
На каждом из них произойдёт одинаковое падение напряжения: U1, U2, U3.
Параллельное соединение
При выполнении данного вида соединения одноимённые выводы соединяются попарно, формула имеет вид:
R = (R1 x R2)/ (R1 + R2).
Обычно полученное значение R бывает меньше меньшего из всех значений соединённых элементов.
Последовательное и параллельное соединения
Информация. На практике параллельное или последовательное присоединение применяют, когда нет детали необходимого номинала. Элементы для таких случаев подбирают одинаковой мощности и одного типа, чтобы не получить слабого звена.
Смешанное соединение
Рассчитывать общее сопротивление смешанных соединений возможно, применяя правило объединения. Сначала выбирают все параллельные и последовательные присоединения и составляют эквивалентные схемы замещения. Их начинают рассчитывать, используя формулы для каждого случая. Из полученной более простой схемы вновь выделяют параллельные и последовательные звенья и опять производят расчёты. Делают это до тех пор, пока не получат самое элементарное соединение или один эквивалентный элемент. Вычисленный результат будет являться искомым.
Метод расчёта при смешанном соединении
Мощность
Одного поиска значения сопротивления недостаточно для того, чтобы применить деталь. Необходимо узнать, на какую мощность должен быть рассчитан элемент. В противном случае он будет перегреваться и выйдет из строя. Мощные детали при поверхностном монтаже лучше устанавливать на радиатор.
Расчет мощности резистора выполняется по формуле:
Р = I² * R = U²/R,
где:
- Р – мощность, Вт;
- I – ток, А;
- U – напряжение, В;
- R – сопротивление, Ом.
После определения мощности резисторов по формуле подбирают комплектующие, исходя из графического обозначения на схемах.
Основные обозначения мощности резисторов
Параллельное соединение проводов электропроводки
Бывают безвыходные ситуации, когда срочно нужно проложить проводку, а провода требуемого сечения в наличии нет. В таком случае, если есть провод меньшего, чем необходимо, сечения, то можно проводку сделать из двух и более проводов, соединив их параллельно. Главное, чтобы сумма сечений каждого из них была не меньше расчетной.
Например, есть три провода сечением 2, 3 и 5 мм2, а нужен по расчетам 10 мм2. Соединяете их все параллельно, и проводка будет выдерживать ток до 50 ампер. Да Вы и сами многократно видели параллельное соединение большего количества тонких проводников для передачи больших токов.
Например, для сварки используется ток до 150 А и для того, чтобы сварщик мог управлять электродом, нужен гибкий провод. Его и делают из сотен параллельно соединенных тонких медных проволочек. В автомобиле аккумулятор к бортовой сети тоже подключают с помощью такого же гибкого многожильного провода, так как во время пуска двигателя стартер потребляет от аккумулятора ток до 100 А.
А при установке и снятии аккумулятора необходимо провода отводить в сторону, то есть провод должен быть достаточно гибким. Способ увеличения сечения электропровода путем параллельного соединения нескольких проводов разного диаметра можно использовать только в крайнем случае. При прокладке домашней электропроводки допустимо соединять параллельно только провода одинакового сечения, взятые из одной бухты.

Как найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно
Вам это будет интересно Особенности индуктивного сопротивления
Измерение напряжения
По каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t
Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Проверочные задачи по теме: магнитное взаимодействие токов и сила Ампера
Задача 1. Докажите, что два параллельных проводника, в которых текут токи одного направления, притягиваются.
Анализ задачи:
Вокруг любого проводника с током существует магнитное поле, следовательно, каждый из двух проводников находится в магнитном поле другого. На первый проводник действует сила Ампера со стороны магнитного поля, созданного током во втором проводнике, и наоборот. Определив по правилу левой руки направления этих сил, выясним, как вести себя проводники.
Решение:
Определим направление силы Ампера, действующая на проводник А, находящегося в магнитном поле проводника В.
1) С помощью правила буравчика определим направление линий магнитной индукции магнитного поля, созданного проводником В (рисунок слева). Выясняется, что у проводника А магнитные линии направлены к нам (отметка «•»).
2) Воспользовавшись правилом левой руки, определим направление силы Ампера, действующая на проводник А со стороны магнитного поля проводника В.
3) Приходим к выводу: проводник А привлекается к проводнику В.
Теперь найдем направление силы Ампера, действующая на проводник В, находится в магнитном поле проводника А.
1) Определим направление линий магнитной индукции магнитного поля, созданного проводником А (рисунок справа). Выясняется, что у проводника В магнитные линии направлены от нас (отметка «х»).
2) Определим направление силы Ампера, действующая на проводник В.
3) Приходим к выводу: проводник В привлекается к проводнику А.
Ответ: два параллельных проводника, в которых текут токи одного направления, действительно притягиваются.
Задача 2. Прямой проводник (стержень) длиной 0,1 м массой 40 г находится в горизонтальном однородном магнитном поле индукцией 0,5 Тл. Стержень расположен перпендикулярно магнитных линий поля). Ток какой силы и в каком направлении следует пропустить в стержне, чтобы он не давил на опору (завис в магнитном поле)?
Анализ задачи:
Стержень не будет давить на опору, если сила Ампера уравновесит силу тяжести. Это произойдет при следующих условиях:
- сила Ампера будет направлена противоположно силе тяжести (то есть вертикально вверх)
- значение силы Ампера равна значению силы тяжести FA = Fтяж
Направление тока определим, воспользовавшись правилом левой руки.
Решение:
Определим направление тока. Для этого расположим левую руку так, чтобы линии магнитного поля входили в ладонь, а отогнутый на 90 ° большой палец был направлен вертикально вверх. Четыре вытянутые пальцы укажут направление от нас. Итак, ток в проводнике следует направить от нас.
Учитываем, что FA = Fтяж. FA= BIlsinα, где sin α = 1; Fтяж = mg
Из последнего выражения найдем силу тока: I = mg/Bl
Проверим единицу, найдем значение искомой величины.
Подводим итоги
Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Значение силы Ампера вычисляют по формуле: FA= BIlsinα, где B — индукция магнитного поля; I — сила тока в проводнике; l — длина активной части проводника; α — угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Для определения направления магнитной силы Ампера используют правило левой руки: если левую руку расположить так, чтобы линии магнитного поля входили в ладонь, а четыре вытянутые пальцы указывали направление тока в проводнике, то отогнутый на 90 ° большой палец укажет направление силы Ампера.
Достоинства и недостатки медных проводов
Медь — это пластичный переходный металл. Имеет золотисто-розовый цвет, встречается в природе в виде самородков. Используется человеком с давних времен — в его честь была названа целая эпоха.
В таблице дано удельное электрическое сопротивление стали и других металлов
Сегодня медные провода часто используют в электронных устройствах. К их достоинствам относятся:
- Высокая электропроводность (металл занимает второе место по этому показателю, уступая только серебру). По сравнению с алюминием медь эффективнее в 1,7 раза: при равном сечении медный кабель пропускает больше тока.
- Сварку, пайку и лужение можно проводить без использования дополнительных материалов.
- Провода обладают хорошей эластичностью и гибкостью, их можно сворачивать и сгибать без особого вреда.
Медь лишь немного уступает серебру
Однако до недавнего времени медные провода проигрывали алюминиевым из-за нескольких недостатков:
- Высокая плотность: при разных размерах медный провод будет весить больше, чем алюминиевый;
- Цена: алюминий в несколько раз дешевле;
- Медь окисляется на открытом воздухе: впрочем, это не влияет на ее работу и легко устраняется.
Как определить сечение кабеля по диаметру, формула, таблица
Самым главным при монтаже электропроводки — это подобрать качественный кабель, ведь всегда с легкостью можно заменить розетку, или выключатель, а заменить прогоревший кабель будет затруднительно, не говоря уже о том, какие могут быть последствия от этого. Очень часто сечение кабеля отличается от заявленного производителем, ведь уменьшение сечения позволяет недобросовестным производителям экономить на самой дорогой составляющей — меди. Чтоб не стать жертвой обмана желательно перед покупкой кабеля измерить его сечение самому, а как определить сечение кабеля по диаметру тремя простыми способами мы расскажем в этой статье.
Способ №1 — с помощью штангенциркуля или микрометра
С помощью штангенциркуля или микрометра замеряется диаметр зачищенной от изоляции токопроводящей жилы кабеля. Замер желательно произвести на нескольких участках жилы, а также на всех жилах кабеля, и записать наименьшие показатели. Если производить замеры с помощью микрометра, то замер нужно производить на ровном участке жилы, так показатели будут более точными.
- Как известно из школьного курса математики площадь круга (а в нашем случае это будет площадь сечения кабеля) исчисляется по формуле S=πR² и если эту формулу упростить делением числа π на 4, то в результате получим формулу по которой можно определить сечение кабеля по диаметру:
- По этой формуле можно с легкостью посчитать сечение токопроводящей жилы, например: при измерении диаметра токопроводящей жилы мы получили значение 1,6 мм, умножаем 0,785*1,6*1,6=4,009466 мм², получается это кабель сечением 4 квадрата.
Способ №2 — с помощью линейки
Что делать если под рукой нет ни штангенциркуля, или, том более микрометра, как определить сечение кабеля по диаметру без этих инструментов? На помощь придет старый и проверенный способ измерения с помощью линейки и карандаша.
Принцип измерения с помощью данного способа состоит в следующем: очищенная жила наматывается на карандаш, как показано на рисунке ниже. Минимальное количество витков должно быть 15-20, но тут тоже нужно исходить из толщины проводника, если он слишком тонкий то желательно намотать витков побольше.
Чтоб уменьшить погрешность измерения, витки нужно наматывать как можно плотнее. Далее с помощью линейки измеряем длину намотанного провода и разделяем на количество витков, получаем диаметр жилы, все просто.
С помощью известной уже нам формулы определяем сечение кабеля по диаметру. Для наглядности приведем пример: допустим мы намотали 20 витков провода, и получили результат 19,6 мм, делим это число на количество витков 20, и получаем диаметр 0,98 мм. С помощью формулы рассчитываем: 0,785*0,98*0,98=0,753914 мм², округляем, и получаем 0,75 квадратов.
Недостаток данного способа определения сечение кабеля по диаметру в том, что с его помощью будет затруднительно намотать провод с большим сечением, а вот для малых сечений этот метод наоборот даст более точный результат. К тому же нужно будет наверняка купить для проверки кусок провода, ведь никакой продавец не позволит проводить у себя такие эксперименты.
Способ №3 — с помощью таблицы
Самый простой способ определить сечение кабеля по диаметру, но все таки потребуется измерительный инструмент штангенциркуль, или микрометр. Измеряем толщину диаметра жилы, и с помощью таблицы определяем сечение.
| Диаметр проводника, мм | Сечение кабеля, мм.кв. |
| 0,80 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1,0 |
| 1,38 | 1,5 |
| 1,60 | 2,0 |
| 1,78 | 2,5 |
| 2,26 | 4,0 |
| 2,76 | 6,0 |
| 3,57 | 10,0 |
| 4,51 | 16,0 |
| 5,64 | 25,0 |
| 6,68 | 35,0 |
| 7,98 | 50,0 |
| 9,44 | 70,0 |
| 11,00 | 95,0 |
| 12,36 | 120,0 |
| 13,82 | 150,0 |
| 15,35 | 185,0 |
| 17,48 | 240,0 |
| 19,54 | 300,0 |
| 22,57 | 400,0 |
В заключении нужно сказать, что важно также обращать внимание на состав токопроводящей жилы, чаще всего подделывают провода и кабеля с медной жилой. Покупайте кабельную продукцию у проверенного продавца
Наш магазин реализует только качественную, сертифицированную продукцию проверенных отечественных производителей.
Если хотите задать вопрос связанный с вопросом выбора кабельной продукции, то Вы всегда можете проконсультироваться с нашими консультантами, достаточно всего лишь связаться с нами через форму обратной связи, либо заказать обратный звонок.
Общие сведения
Упорядоченное движение носителей заряда в физическом теле называют электрическим током. Ими могут быть различные элементарные частицы. Например, в проводниках — электроны, электролитах — ионы. В состоянии покоя, то есть когда на тело не оказывается постороннее воздействие, движение носителей хаотичное. В результате происходит компенсирование зарядов, и ток не возникает. Если же к веществу приложить силу или деформировать его, направление движения частиц станет упорядоченным и возникнет электрический ток.
Все существующие вещества характеризуются физическими и химическими свойствами. Среди них и проводимость. Это электрическая величина, определяющая способность тела пропускать через себя ток. По своему строению все материалы делятся на 3 класса:
- проводники — вещества, не оказывающие сопротивление прохождению тока;
- полупроводники — тела, в которых величина проводимости зависит от чистоты материала, температуры и вида воздействующего излучения;
- диэлектрики — вещества, практически не проводящие электрический ток.
За единицу измерения силы тока принят Ампер, показывающий, какое количество электричества проходит через поперечное сечение проводника за одну секунду: I = q / t = кулон / секунду = ампер.
Электрическое сопротивление тела зависит от природы носителей заряда и геометрии материала. Это скалярный параметр. При его расчёте используют понятие удельное сопротивление. Выражают его в омах, умноженных на метр, и обозначают греческой буквой р. По физическому смыслу величина является обратным параметром удельной проводимости.
С ней, кроме сопротивления и силы тока, тесно связано и напряжение. С физической точки зрения, это работа, которую выполняет электрическое поле при переносе единичного заряда из одной точки в другую. В Международной системе величин напряжение принято обозначать в вольтах: U = f2- f1, где f — значения потенциала заряда в точках.
Содержание книги
Предыдующая страница
§12. Постоянное магнитное поле
12.7 Расчет индукции магнитного поля.
Закон Био-Саварра-Лапласа и принцип суперпозиции позволяют рассчитать индукцию магнитного поля (~vec B) , создаваемого произвольной системой электрических токов, в произвольной точке пространства. Для этого необходимо разбить все токи на бесконечно малые участки (~(I Delta vec l)_k) , записать выражения для векторов для индукции поля (~(Delta vec B)_k) , создаваемых этими элементами (пользуясь законом Био-Саварра-Лапласа) и просуммировать полученные выражения (что позволяет принцип суперпозиции) для всех участков тока
(~vec B = sum_{k} {(Delta vec B)_k}) . (1)
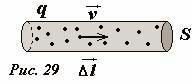
Рассмотрим еще раз участок проводника с током (Рис. 29) . Выражение для элемента тока (~I Delta vec l) записывается также в виде (~I Delta vec l = vec j S Delta l = vec j Delta V) . В том случае, когда электрические токи не являются линейными, а пространственно распределенными (то есть текут не только по тонким проводам), выражение для элемента тока (~I Delta vec l) следует заменить эквивалентным (~vec j Delta V) и провести суммирование по всем элементам объема., где протекают электрические токи.
Конечно, такое суммирование часто представляет собой громоздкую математическую задачу (в конце концов, для его выполнения можно воспользоваться компьютером), но, с физической точки зрения, изложенный метод дает полное решение задачи.
Рассмотрим несколько примеров расчета индукции магнитного поля по изложенной выше методике.
12.7.1 Магнитное поле кругового тока.
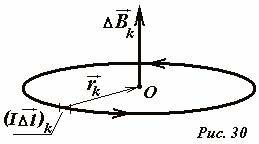
Пусть постоянный электрический ток силой I протекает по плоскому круглому контуру радиуса R. Найдем индукцию поля в центре кольца в точке O (Рис. 30). Мысленно разобьем кольцо на малые участки, которые можно считать прямолинейными, и применим закон Био-Саварра-Лапласа для определения индукции поля, создаваемого этим элементом, в центре кольца. В данном случае вектор элемента тока (~(I Delta vec l)_k) и вектор (~vec r_k) , соединяющий данный элемент с точкой наблюдения (центр кольца), перпендикулярны, поэтому (sin alpha = 1) . Вектор индукции поля, созданного выделенным участком кольца, направлен вдоль оси кольца, а его модуль равен
(~Delta B_k = frac{mu_0}{4 pi} frac{(I Delta l)_k}{R^2}) . (1)
Для любого другого элемента кольца ситуация абсолютно аналогична – вектор индукции также направлен по оси кольца, а его модуль определяется формулой (1). Поэтому суммирование этих векторов выполняется элементарно и сводится к суммированию длин участков кольца
(~B = sum_k Delta B_k = sum_k frac{mu_0}{4 pi} frac{(I Delta l)_k}{R^2} = frac{mu_0}{4 pi} frac{I}{R^2} sum_k (Delta l)_k = frac{mu_0}{4 pi} frac{I}{R^2} 2 pi R = frac{mu_0 I}{2 R}) . (2)
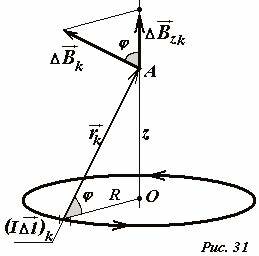
Усложним задачу — найдем индукцию поля в точке A, находящейся на оси кольца на расстоянии z от его центра (Рис. 31). По-прежнему, выделяем малый участок кольца (~(I Delta vec l)_k) и строим вектор индукции поля (~(Delta vec B)_k) , созданным этим элементом, в рассматриваемой точке. Этот вектор перпендикулярен вектору (~vec r) , соединяющему выделенный участок с точкой наблюдения. Векторы (~(I Delta vec l)_k) и (~vec r_k) , как и ранее, перпендикулярны, поэтому (sin alpha = 1) . Так кольцо обладает осевой симметрией, то суммарный вектор индукции поля в точке A должен быть направлен по оси кольца. К этому же выводу о направлении суммарного вектора индукции можно прийти, если заметить, что каждому выделенному участку кольца имеется симметричный ему с противоположной стороны, а сумма двух симметричных векторов направлена вдоль оси кольца. Таким образом, для того чтобы определить модуль суммарного вектора индукции, необходимо просуммировать проекции векторов на ось кольца. Эта операция не представляет особой сложности, если учесть, расстояния от всех точек кольца до точки наблюдения одинаковы (~r = r_k = sqrt{R^2 + z^2}) , а также одинаковы углы φ между векторами (~(Delta vec B)_k) и осью кольца. Запишем выражение для модуля искомого суммарного вектора индукции
(~B = sum_k Delta B_{zk} = sum_k frac{mu_0}{4 pi} frac{(I Delta l)_k}{r^2} cos varphi = frac{mu_0}{4 pi} frac{I cos varphi}{r^2} sum_k (Delta l)_k = frac{mu_0}{4 pi} frac{I cos varphi}{r^2} 2 pi R = frac{mu_0 I R}{2 r^2} cos varphi) .
Из рисунка следует, что (~cos varphi = frac{R}{r}) , с учетом выражения для расстояния r, получим окончательное выражение для вектора индукции поля
(~B = frac{mu_0 I R}{2 r^2} cos varphi = frac{mu_0 I R^2}{2 r^3} = frac{mu_0 I}{2} cdot frac{R^2}{(R^2 + z^2)^frac{3}{2}}) . (3)
Как и следовало ожидать, в центре кольца (при z = 0) формула (3) переходит в полученную ранее формулу (2).
Задания для самостоятельной работы.
- Постройте график зависимости индукции поля (3) от расстояния до центра кольца.
- Сравните полученную зависимость (3) с выражением для модуля напряженности электрического поля, создаваемого равномерно заряженным кольцом (§9.6). Объясните возникшие принципиальные различия между этими зависимостями.
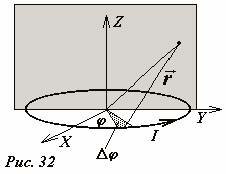
Используя общий рассматриваемый здесь метод, можно рассчитать индукцию поля в произвольной точке. Рассматриваемая система обладает осевой симметрией, поэтому достаточно найти распределение поля в плоскости, перпендикулярной плоскости кольца и проходящей через его центр. Пусть кольцо лежит в плоскости xOy (рис.32), а поле рассчитывается в плоскости yOz. Кольцо следует разбить на малые участки, видимые из центра под углом Δφ и просуммировать поля создаваемые этими участками. Можно показать (попробуйте проделать это самостоятельно), что компоненты вектора магнитной индукции поля, создаваемого одним выделенным элементом тока, в точке с координатами (y,z) рассчитываются по формулам:
(~begin{matrix} r_k = sqrt{x^2 + y^2 — 2xR cos varphi_k +1} ; \ Delta B_{yk} = -frac{mu_0}{4 pi} frac{z cos varphi_k}{r^3_k} Delta varphi ; \ Delta B_{zk} = -frac{mu_0}{4 pi} frac{1 — y cos varphi_k}{r^3_k} Delta varphi . end{matrix}) (4)
Необходимое суммирование не может быть проведено аналитически, так как при переходе от одного участка кольца к другому изменяются расстояния до точки суммирования. Поэтому «простейший» способ провести такое суммирование – использовать компьютер.
Если же известно значение вектора индукции (или хотя бы имеется алгоритм его расчета) в каждой точке, то можно построить картину силовых линий магнитного поля. Очевидно, что алгоритм построения силовых линий векторного поля не зависит от его физического содержания, а такой алгоритм был кратко рассмотрен нами при изучении электростатики.

На рис. 33 картина силовых линий рассчитана при разбиении кольца на 20 частей, этого оказалось вполне достаточно, так как и при 10 интервалах разбиения получался практически тот же рисунок.
Рассмотрим выражение для индукции поля на оси кольца на расстояниях значительно больших радиуса кольца z >> R. В этом случае формула (3) упрощается и приобретает вид
(~B = frac{mu_0 I}{2} cdot frac{R^2}{(R^2 + z^2)^frac{3}{2}} approx frac{mu_0 I}{2} cdot frac{R^2}{z^3} = frac{mu_0 I}{2 pi} cdot frac{pi R^2}{z^3} = frac{mu_0 p_m}{2 pi z^3}) , (5)
где (I pi R^2 = IS = p_m) — произведение силы тока на площадь контура, то есть магнитный момент кольца. Эта формула совпадает (если как обычно, заменить μ0 в числителе на ε0 в знаменателе) с выражением для напряженности электрического поля диполя на его оси.

Такое совпадение не случайно, более того, можно показать, что подобное соответствие справедливо для любой точки поля, находящейся на больших расстояниях от кольца. Фактически малый контур с током является магнитным диполем (два одинаковых малых противоположно направленных элемента тока) – поэтому его поле совпадает с полем электрического диполя. Чтобы ярче подчеркнуть этот факт, на рис. 34 приведена картина силовых линий магнитного поля кольца, на больших расстояниях от него (сравните с аналогичной картиной для поля электрического диполя).
12.7.2 Магнитное поле прямого тока.
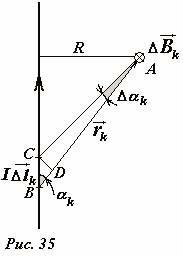
Рассчитаем индукцию магнитного поля, создаваемого бесконечным [1] проводником, по которому протекает электрический ток силой I (Рис. 35) Методика расчет остается прежней: мысленно разбиваем проводник на малые участки (~I Delta vec l_k). Согласно закона Био-Саварра-Лапласа в произвольной точке A, находящейся на расстоянии R от проводника, произвольный элемент тока создает магнитное поле, вектор индукции которого (~(Delta vec B)_k) направлен перпендикулярно плоскости, содержащей проводник и рассматриваемую точку (на Рис. 35 — перпендикулярно плоскости рисунка), модуль этого вектора равен
(~Delta B_k = frac{mu_0}{4 pi} frac{I Delta l_k}{r^2_k} sin alpha_k) , (1)
где rk — расстояние от выбранного участка проводника до точки наблюдения, αk — угол между проводником и направлением от элемента тока до точки наблюдения.
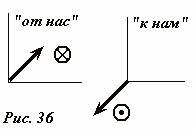
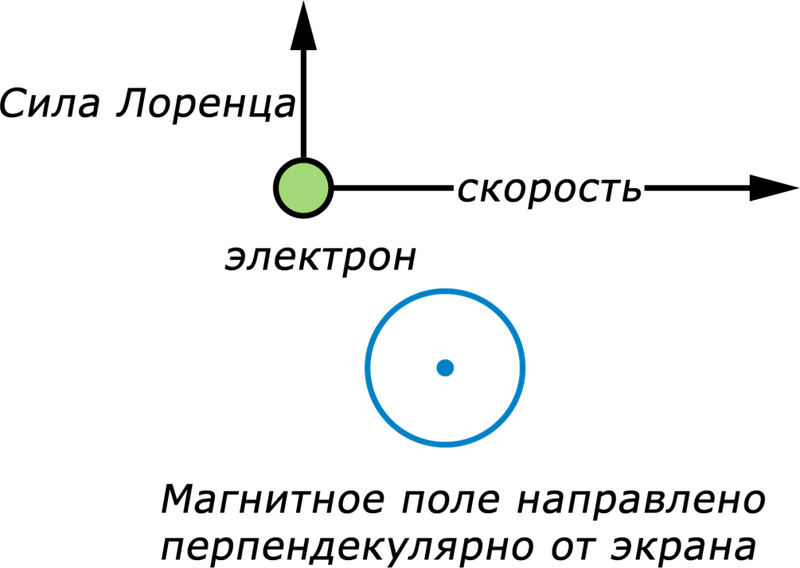
Договоримся об еще одном общепринятом соглашении. Достаточно часто приходится изображать векторы, перпендикулярные плоскости рисунка. В этом случае эти векторы изображаются в виде (рис. 36): небольшого кружка с точкой в центре, если вектор направлен «на нас» (видно «острие» вектора); кружка с перекрестием, если вектор направлен от нас (видно «оперение» вектора).
Векторы поле, созданных всеми другими участками проводника, направлены также, поэтому суммирование векторов в данном случае сводится к суммированию их модулей. Но даже вычислить сумму модулей не просто, так как для различных участков проводника расстояния rk и αk различны. Тем не менее, такое суммирование выполнимо, его результат выражается формулой, определяющей величину индукции магнитного поля бесконечного прямого тока
(~B_k = sum_k Delta B_k = sum_k frac{mu_0}{4 pi} frac{I Delta l_k}{r^2_k} sin alpha_k = frac{mu_0 I}{4 pi} sum_k (frac{Delta l_k}{r^2_k} sin alpha_k) = frac{mu_0 I}{2 pi R}) , (2)
здесь не приведено вычисление последней суммы (которая равна (~sum_k frac{Delta l_k}{r^2_k} sin alpha_k = frac{2}{R})), поверьте пока в справедливость полученного выражения, хотя бы потому, что оно имеет богатый физический смысл. Во-первых, эта формула совпадает с выражением для напряженности электрического поля, создаваемого бесконечной прямой равномерно заряженной нитью; во-вторых, оно соответствует результату опытов А.М. Ампера по изучению взаимодействия параллельных токов. Действительно, если один проводник создает магнитное поле, индукция которого обратно пропорциональна расстоянию до проводника, то на второй проводник действует сила Ампера, пропорциональная индукции поля, то есть обратно пропорциональная расстоянию между проводниками.
Дадим теперь строгий вывод формулы для суммы, фигурирующей в выражении (2). Проще всего она выводится с помощью операции интегрирования, но здесь мы дадим ее геометрический вывод. Для начала с помощью рис. 35 преобразуем каждое слагаемое этой формулы (~frac{Delta l_k}{r^2_k} sin alpha_k) . Заметим, что произведение (~Delta l_k sin alpha_k) равно длине отрезка CD, перпендикулярного вектору (~vec r_k) — (~Delta l_k sin alpha_k = |CD|) . Отношение же длины этого отрезка к расстоянию rk для малых длин элементов тока равно малому углу Δαk, под которым виден выделенный участок проводника
(~frac{Delta l_k}{r_k} sin alpha_k = frac{|CD|}{r_k} = Delta alpha_k) (3)
( точнее, это отношение равно тангенсу угла, который для малых углов равен самому углу, измеренному в радианах). Из того же рисунка следует, что отношение (~frac{r_k}{sin alpha_k} = R) равно расстоянию от точки наблюдения до проводника и не зависит от выбора участка проводника. С учетом этого соотношения и формулы (2) получим
(~frac{Delta l_k}{r^2_k} sin alpha_k = frac{Delta alpha_k}{r_k} = frac{Delta alpha_k sin alpha_k}{R}) .
Таким образом, вычисление суммы (2) сводится к вычислению суммы (~sum_k Delta alpha_k sin alpha_k) , в которой все углы являются малыми (поэтому число слагаемых велико), пусть углы αk изменяются от нуля до некоторого предельного значения αmax.
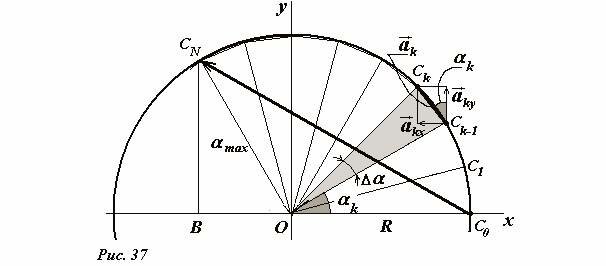
Для вычисления этой суммы применим искусственный прием (он встретится нам и в дальнейшем). Возьмем окружность (Рис. 37) радиуса R и разобьем ее точками C0, C1, C2, …, CN на малые участки, угловой размер каждого равен Δα.
Хорды, которые образованы точками разбиения будем рассматривать как векторы (~vec a_0 = overrightarrow {C_0 C_1}, vec a_1 = overrightarrow {C_1 C_2}, ldots, vec a_k = overrightarrow {C_k C_{k+1}}, ldots) . Сумма этих векторов очевидна – это вектор (~vec A) , соединяющий начальную и конечную точки разбиения окружности:
(~sum_k vec a_k = overrightarrow {C_0 C_N} = vec A) . (4)
Теперь, внимание, если справедливо векторное равенство, то справедливо аналогичное выражение для любой проекции этих векторов. Введем декартовую систему координат с началом в центре окружности, ось Ox которой проходит через начальную точку. Длины построенных вписанных векторов равны (~|vec a_k| = R Delta alpha_k) (точнее, это длина дуги, но для малых углов, длина стягивающей хорды стремится к длине дуги). Из рисунка 37 следует, что проекции этого вектора на оси координат равны, соответственно,
(~a_{kx} = -R Delta alpha_k sin alpha_k ; a_{ky} = R Delta alpha_k cos alpha_k) .
Проецируя равенство (4) на оси координат получим
(~begin{matrix} (vec A)_x = (overrightarrow {C_0 C_N})_x = -|C_0 B| = sum_k a_{kx} = -sum_k R Delta alpha_k sin alpha_k \ (vec A)_y = (overrightarrow {C_0 C_N})_y = -|C_N B| = sum_k a_{ky} = sum_k R Delta alpha_k cos alpha_k end{matrix} ) . (5)
Проекции суммарного вектора (~vec A) на оси координат находятся просто
(~begin{matrix} (vec A)_x = (overrightarrow {C_0 C_N})_x = -|C_0 B| = -(R + R cos (pi — alpha_{max})) = R(1 — cos alpha_{max}) \ (vec A)_y = (overrightarrow {C_0 C_N})_y = -|C_N B| = R sin (pi — alpha_{max}) = R sin alpha_{max} end{matrix} ) . (6)
Сравнивая выражения (5) и (6) получим искомые формулы
(~sum_k sin alpha_k Delta alpha_k = 1 — cos alpha_{max}; sum_k cos alpha_k Delta alpha_k = sin alpha_{max}) . (7)
Еще раз подчеркнем, что суммирование в этих формулах проводится в пределах изменения угла от нуля до предельного значения αmax.
Осталось принять во внимание, что бесконечный прямой проводник виден из любой точки вне его под углом αmax = π, поэтому искомая сумма выражается формулой
(~sum_k frac{Delta l_k}{r^2_k} sin alpha_k = sum_k frac{Delta alpha_k sin alpha_k}{R} = frac{1 — cos pi}{R} = frac{2}{R}) ,
что и требовалось доказать.
Оценим длину «бесконечного» в данном случае проводника – во сколько раз длина проводника должна быть больше расстояния до точки наблюдения, что бы погрешность расчета индукции поля по формуле (2), примененной к проводнику конечной длины, была пренебрежимо малой.
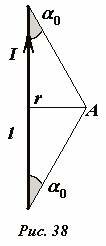
Пусть длина прямого проводника равна l, а индукция поля рассчитывается в точке A, находящейся на расстоянии r (считаем, что r << l) от центра проводника (Рис. 38). С помощью полученных формул можно получить точное выражение для индукции поля в рассматриваемой точке (~bar{B} = frac{mu_0 I}{2 pi r} cos alpha_0) , где α0 — угол между проводником и направлением на точку наблюдения с конца проводника.
Если считать проводник бесконечно длинным, то индуктивность поля должна рассчитываться по формуле (которую в данном случае следует считать приближенной) (~tilde{B} = frac{mu_0 I}{2 pi r}) . Относительная погрешность этой формулы равна [2]
(~varepsilon = frac{tilde{B} — bar{B}}{bar{B}} = frac{1}{cos alpha_0} — 1 = frac{sqrt{left (frac{l}{2} right )^2 + r^2}}{frac{l}{2}} — 1 = sqrt{1 + 4 frac{r^2}{l^2}} — 1 approx 2 frac{r^2}{l^2}) .
Такая ошибка будет допущена, если отношение длины проводника к расстоянию до точки наблюдения равно (~frac{l}{r} = frac{2}{varepsilon}). Так для относительной ошибки ε = 1% искомое отношение равно (~frac{l}{r} approx 15). Итак, в рассмотренном случае «бесконечность» равна 15.
Примечания
- ↑ Конечно, «бесконечно длинный» значит, что его длина значительно превышает расстояние до той точки, где измеряется поле.
- ↑ Используя известную приближенную формулу (~(1 + x)^beta approx 1 + beta x) (в данном случае (beta = frac{1}{2})).
Следующая страница
Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.
Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Магнетизм: определение
Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.
Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.
Магнитная индукция
Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.
Магнитная индукция – это силовая векторная характеристика магнитного поля.
Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.
Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.
Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.
Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!
Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.
Сила Ампера
Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.
Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.
Сила Лоренца
Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.
Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:
Взаимодействие токов
Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.
В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.
Во втором случае магнитная индукция в центре кругового витка с током равна:
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Магнитный поток и ЭДС
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.
Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:
Формула для ЭДС самоиндукции:
Энергия магнитного поля
Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:
Объемная плотность энергии поля:
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.