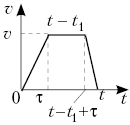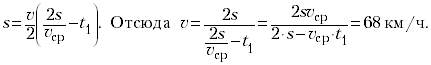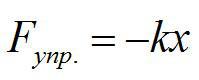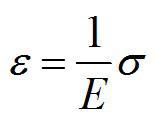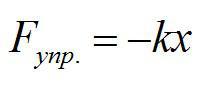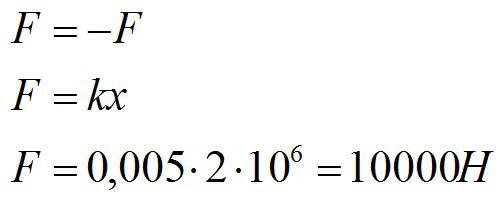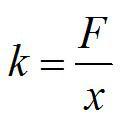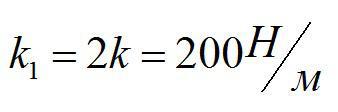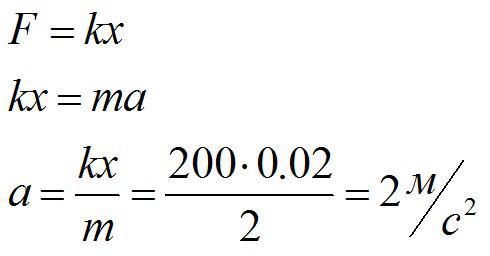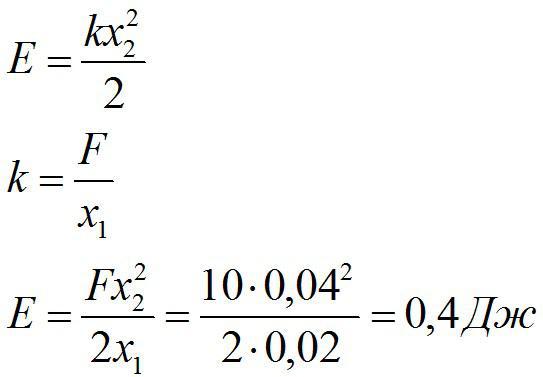Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
- сдвиг;
- кручение;
- изгиб;
- сжатие/растяжение;
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.
Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение
Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
[ large L_{0} + Delta L = L ]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).
[ large boxed{ Delta L = L — L_{0} }]
( L_{0} left(text{м} right) ) – начальная длина пружины;
( L left(text{м} right) ) – конечная длина растянутой пружины;
( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;
Величину ( Delta L ) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]
( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.
[ large boxed{ F_{text{упр}} = k cdot Delta L }]
Эту формулу назвали законом упругости Гука.
( F_{text{упр}} left( H right) ) – сила упругости;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
[ large F_{text{упр}} — m cdot g = 0 ]
Подставим в это уравнение выражение для силы упругости
[ large k cdot Delta L — m cdot g = 0 ]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:
[ large boxed{ k = frac{ m cdot g }{Delta L} }]
(g) – ускорение свободного падения, оно связано с силой тяжести.
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две параллельные пружины:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]
Умножим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{параллел}} = 2k_{1} } ]
Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).
Одна пружина:
[ large k_{1} cdot Delta L = m cdot g ]
Две последовательные пружины:
[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]
Так как правые части уравнений совпадают, левые части тоже будут равны:
[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]
Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:
[ large k_{text{послед}} cdot 2 = k_{1} ]
Разделим обе части полученного уравнения на число 2:
[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]
Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]
( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;
( Delta L left(text{м} right) ) – удлинение пружины;
( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.
Выводы
- Упругие тела – такие, которые сопротивляются деформации;
- Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
- Деформация – изменение формы, или размеров тела;
- Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
- Удлинение пружины – это разность ее конечной и начальной длин;
- Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
- Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
- Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
- А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,662 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,985 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Работа с графиками на уроках
Г.В.РЫБКИНА,
МОУ СОШ № 80, г. Воронеж
Работа с графиками на уроках
Открытый урок решения задач.
Подготовка к итоговому контролю
за курс основной школы. 9-й класс
Важность графического метода в
обучении физике велика. Можно утверждать, что
именно использование графиков является
необходимым условием сознательного усвоения
учебного материала, выработки более чёткого
понимания физических законов. Графическое
представление физического процесса делает его
более наглядным и тем самым облегчает понимание
рассматриваемого явления, способствует развитию
абстрактного мышления, интуиции, умения
анализировать и сравнивать, находить более
рациональный способ решения задач. (Вопрос об
использовании графиков становится всё более
актуальным, т.к. КИМы ЕГЭ содержат до 25%
графических заданий.) Кроме того, применение
графического метода способствует укреплению
связей физики с математикой, наполняет
абстрактные математические закономерности
конкретным физическим содержанием.
Можно выделить следующие приёмы
работы с графиками, которые образуют целостную
систему: работа с предложенными графиками,
построение графиков, решение задач графическим
способом, графическое отображение результатов
измерений при выполнении лабораторных работ и
работ практикума.
Творческий учитель может
самостоятельно сконструировать совокупность
вопросов-заданий различной сложности к
конкретной графической зависимости, которые
можно использовать в рамках вариативных учебных
технологий. Приведём примеры.
Работа с предложенными графиками.
Можно:
– определять функциональную
зависимость между предложенными физическими
величинами;
– находить по значению известной
величины значение неизвестной;
– находить значения величины,
производной от отложенных по осям величин;
– объяснять особенности протекания
физического процесса, для которого построен
график;
– выявлять сходство и различия
свойств изучаемых тел и веществ при сравнении
графиков;
– составлять задачи;
– составлять таблицу значений
соответствующих физических величин по их
графической зависимости;
– идентифицировать объект, для
которого построен график.
1. 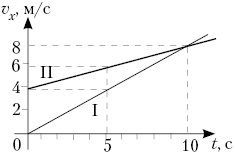
По графикам зависимости проекции
скорости прямолинейного движения от времени для
двух тел определите:
1) характер зависимости скорости от
времени для тела I и тела II;
2) характер движения этих тел;
3) а) начальные скорости тела I и
тела II; б) скорость тела II через 5 c от момента
начала отсчёта времени; в) промежуток
времени от момента начала движения тела I до
момента, когда его скорость стала 4 м/с;
4) а) ускорение каждого тела; б)
пути, пройденные каждым телом за 5 с; в)
промежуток времени, за который тела пройдут
равный путь; г) промежуток времени от
начала движения тела I до момента , когда скорости
тел сравняются; сравните пути, пройденные телами
за это время; д) силы, действующие на тела,
если масса I тела 2 кг, масса II тела 3 кг;
5) какое тело движется с бльшим ускорением;
6) для каких объектов могут быть
построены эти графики?
Заполните таблицу:
Составьте свою задачу по предложенным
графикам.
2.
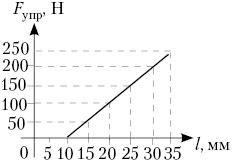
По графику зависимости силы упругости
пружины Fупр от её длины l
определите:
1) какова зависимость между данными
величинами;
2) а) сжимается или растягивается
пружина под действием силы; б) какой закон
отражает этот график; в) сохранится ли эта
зависимость, если и дальше увеличивать длину
пружины;
3) а) какова начальная длина
пружины; б) какой будет длина пружины, если
приложить силу 150 Н; в) какую силу нужно
приложить к пружине, чтобы её длина увеличилась в
2 раза;
4) а) величину деформации l,
вызванную силой 150 Н; б) жёсткость пружины; в)
работу, которую нужно совершить для растяжения
пружины от 15 до 35 мм;
5) в каком случае совершается бльшая работа: при
растяжении пружины от 10 до 20 мм или от 20 до 25 мм?
Докажите, что этот график построен
именно для пружины.
Пользуясь графиком, заполните таблицу:
|
l, мм |
10 | 15 | 20 | 25 | 30 | 35 |
| Fупр , Н | ||||||
| k, Н/м |
6) Составьте свою задачу по
предложенным графикам.
Построение графиков. Можно
вычерчивать:
– графики по табличным данным;
– графики по формулам, выражающим
физическую закономерность;
– схематические графики;
– один график по данным другого.
После построения графика можно
работать с ним, как показано выше .
1. Трактор развивает тяговое усилие 7
кН. Постройте график зависимости силы тяги
трактора F от пройденного пути s. а)
Что представляет собой график? б) Как по
графику найти работу, совершённую трактором при
перемещении сельскохозяйственных орудий на
расстояние 0,4 км?
2. Постройте кривую суточного
изменения атмосферного давления на протяжении
одной недели. Проанализируйте этот график,
ответив на вопросы: а) Какое самое малое
давление было отмечено? б) Какое самое
большое давление было отмечено? в) Сколько
дней давление было выше нормального? г) На
сколько изменилось атмосферное давление между
пятыми и шестыми сутками?
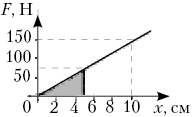
3. При упругом удлинении пружины на 10 см
возникает сила упругости 150 Н. Постройте график
зависимости Fупр(x) и определите: а) работу,
которую необходимо совершить при растяжении
пружины на 5 см; б) жёсткость пружины.
Решение
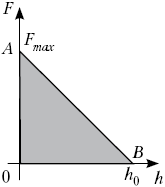
Работа численно равна площади
заштрихованного треугольника:
А = 5 ·10–2 м · 75 Н = 3,75 Дж.
Решение задач графическим
способом. Это метод, основанный на
построении и анализе графика рассматриваемого
процесса или на геометрических построениях. Если
график используется только для иллюстрации
описываемого в задаче явления, то решение задачи
нельзя назвать графическим. Все задачи, решаемые
графически, можно условно разделить на несколько
типов по методу решения:
– графическое решение уравнений
(ответ даётся точками пересечения кривых);
– графическая оценка (определение
условий, при которых наблюдается наибольшее или
наименьшее физическое действие);
– графическое интегрирование (ответ
даётся величиной площади фигуры, ограниченной
кривой, ординатами крайних точек и осью абсцисс);
– графическое усреднение (определение
среднего значения некоторой физической
величины, изменяющейся в определённых пределах).
1. В тот момент, когда мимо станции со
скоростью 5 м/с проходил товарный состав, от
платформы в том же направлении отошёл
пассажирский поезд. Через какое время
пассажирский поезд догнал товарный, если
пассажирский двигался с ускорением 0,3 м/с2,
а товарный – равномерно?
Решение
| t | 0 | 20 | 30 | 40 |
| x1 | 0 | 100 | 150 | 200 |
| t | 0 | 10 | 20 | 30 | 40 |
| x2 | 0 | 15 | 60 | 135 | 600 |
tвстр = 33 c, хвстр =
170 м.
2. Поезд прошёл расстояние s = 17 км
между двумя станциями со скоростью ср= 60 км/ч. При этом на
разгон вначале и торможение перед остановкой
ушло в общей сложности t1 = 4 мин, а
остальное время поезд двигался с постоянной
скоростью. Чему равна эта скорость?
Решение
Пусть – время
разгона поезда, t – общее время в пути. Тогда
С другой стороны,
Поэтому
3. В воде плавает плоская льдина. Какую
работу надо совершить, чтобы полностью погрузить
льдину в воду? (S = 5 м2, H = 0,5 м.)
Решение
Найдём h0 – высоту льдины
над водой:
FА= Fтяж; воды g S (H
– h0) = льда g S H;
В начальный момент FА= Fтяж,
но по мере погружения льдины, т.е. уменьшения её
высоты над водой, необходимо прикладывать всё бльшую силу.
Зависимость F (h) – линейная. Построим
график этой зависимости. Максимальная внешняя
сила:
Fmax = FA – Fтяж
= воды g S
H – льда g S H
= g S H(воды–
льда);
Графическое изображение
результатов измерений при выполнении
лабораторных работ и работ практикума.
Такой тип деятельности необходим для:
– контроля результатов измерений;
– нахождения по графику среднего
значения физической величины;
– проверки правильности результата
методом сведения сложной зависимости
(квадратичной) к линейной (по оси ординат
откладывается не сама величина, а квадрат
величины);
– дальнейшей работы по построенному
графику;
– для определения значения физической
величины методом экстраполирования
(продолжения) графика.
1. 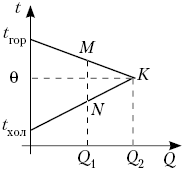
При выполнении лабораторной работы «Сравнение
количеств теплоты при смешивании воды разной
температуры» учащимся можно предложить
построить графики изменения температуры,
подсчитав количество теплоты, отданной холодной
водой и полученной горячей, а затем объяснить,
что означают точки М, N и K графика.
2. При выполнении лабораторной работы
«Градуирование пружины и измерение силы
динамометром» нужно обратить внимание на то, что Fупр
~ l, и построить график зависимости Fупр(
l).
Литература
Ерохина Р.Я. и др. Использование
графического метода и идеи симметрии при решении
физических задач в школе: Методическое пособие.
– Воронеж, 1994.
Золотов В.А. Вопросы и задания по
физике в 6–7 классах. –М.: Просвещение, 1975.
Каменецкий С.Е., Орехов В.П.
Методика решения задач по физике в средней школе.
– М.: Просвещение, 1987.
Лукашик В.И. Сборник вопросов и
задач по физике-6–7. – М.: Просвещение, 1988.
Методика преподавания физики в 7–8
классах средней школы: Под ред. В.П.Орехова,
А.В.Усовой. – М.: Просвещение, 1980.
Резников Л.И. Графический метод в
преподавании физики. – М.: Учпедгиз, 1960.
Рымкевич А.П. Сборник задач по
физике-8–10. – М.: Просвещение, 1987.
Степанова Н.Е. Задачи по физике
для 9–11 классов общеобразовательных учреждений.
– М.: Просвещение, 1997.
Тульчинский М.Е. Качественные
задачи по физике в 6–7 классах. – М.: Просвещение,
1972.
Галина Викторовна Рыбкина –
учитель физики высшей квалификационной
категории, окончила с отличием Воронежский ГПИ в
1989 г., педагогический стаж 18 лет (в одной и той же
школе № 80). Пять лет руководила РМО учителей
физики Коминтерновского района г. Воронежа. В 2007
г. поступила в аспирантуру и сейчас работает над
диссертацией. Замужем, имеет двух дочерей:
старшей 20 лет, она студентка 4-го курса РГО ТУПС,
младшей – 8 лет, учится во 2-м классе. Хобби –
любит и умеет шить, но катастрофически не хватает
времени.
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
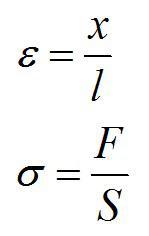
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
По третьему закону Ньютона:
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
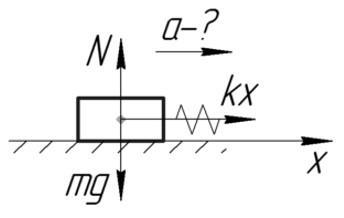
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
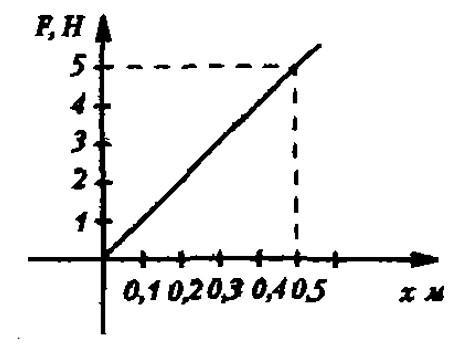
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
К пружине поочередно подвешивали разное количество грузов массой по 102 г и при этом измеряли длину пружины l. Полученные данные записали в таблицу.
| Количество грузов | Модуль силы F, Н | Длина пружины l, см | Удлинение пружины Δl, см |
|---|---|---|---|
| 0 | 0 | 4,0 | 0 |
| 1 | 1 | 4,5 | 0,5 |
| 2 | 5,0 | ||
| 3 | 5,5 | ||
| 4 | 6,0 |
а) Заполните в таблице пустые клетки.
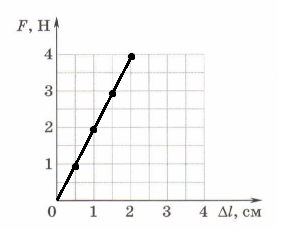
б) Используя данные таблицы, постройте график зависимости приложенной к пружине силы F от её удлинения Δl.
в) Вычислите жёсткость пружины, учитывая, что силу упругости, возникающая в пружине, равна по модулю приложенной к ней силе.
k = __ = __ Н/м.
reshalka.com
ГДЗ Физика 7 класс рабочая тетрадь к учебнику Перышкина автор Ханнанова. Задание 30. Номер №5
Решение а
| Количество грузов | Модуль силы F, Н | Длина пружины l, см | Удлинение пружины Δl, см |
|---|---|---|---|
| 0 | 0 | 4,0 | 0 |
| 1 | 1 | 4,5 | 0,5 |
| 2 | 2 | 5,0 | 1 |
| 3 | 3 | 5,5 | 1,5 |
| 4 | 4 | 6,0 | 2 |
Решение б
Решение в
k =
F
у
п
р
Δ
l
=
2
0
,
01
=
200
Н/м.