Как найти длину пружины при подвешенном грузе - Исправление недочетов и поиск решений вместе с Examum.ru

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

сдвиг;
кручение;
изгиб;
сжатие/растяжение;

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина (L_{0}) пружины.

Рис. 2. Сравнивая длину свободной пружины с длиной нагруженной, можно найти ее удлинение

Подвесим теперь к пружине груз. Пружина будет иметь длину (L), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

[ large L_{0} + Delta L = L ]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину (L_{0}).

[ large boxed{ Delta L = L — L_{0} }]

( L_{0} left(text{м} right) ) – начальная длина пружины;

( L left(text{м} right) ) – конечная длина растянутой пружины;

( Delta L left(text{м} right) ) – кусочек длины, на который растянули пружину;

Величину ( Delta L ) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

[ large boxed{ frac{Delta L }{ L_{0}} = frac{ L — L_{0}}{L_{0} } = varepsilon } ]

( varepsilon ) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал ( F_{text{упр}} ) силой упругости.

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины (Delta L ) пружины. Получим выражение для коэффициента жесткости:

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину (Delta L). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину (Delta L). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину (Delta L).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Рис. 6. Система, состоящая из двух одинаковых пружин, соединенных последовательно, деформируются больше одной пружины

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом (mg).

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{послед}} cdot 2 = k_{1} ]

Разделим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{послед}} = frac{k_{1}}{2} } ]

Коэффициент жесткости (k_{text{послед}}) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину (Delta L ) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Источник

Как найти длину пружины

Длина проволоки, из которой свита пружина, значительно больше длины самой пружины. Чтобы узнать протяженность этой проволоки, необязательно портить пружину, разматывая ее. Достаточно осуществить расчет.

Вам понадобится

— пружина;
— штангенциркуль;
— тиски;
— защитные перчатки;
— защитные очки;
— калькулятор.

Инструкция

Измерьте диаметр пружины в сжатом состоянии при помощи штангенциркуля. Не прилагайте к ней при этом значительных усилий, иначе она сожмется, что исказит результат измерения в сторону уменьшения. Лучше всего измерить диаметр в нескольких местах, после чего найти среднее арифметическое результатов измерения по следующей формуле:D=(D1+D2+D3+…+Dn)/n, где D — средний диаметр, мм, D1…Dn — результаты измерений, мм, n -количество измерений (безразмерная величина).

Найдите длину окружности одного витка по следующей формуле:l=πD, где l — длина окружности в мм, π — число «пи», D — диаметр одного витка (мм).На самом деле виток имеет форму не окружности, а овала (за счет того, что сама проволока обладает ненулевым диаметров, и каждый виток даже в сжатом состоянии имеет диагональное продольное сечение), но удлинение за счет этого столь незначительно, что им можно пренебречь.

Сосчитайте количество витков пружины (обязательно в полностью разжатом состоянии). Чтобы не ошибиться, можно использовать при подсчете витков упругую полоску, например, из гибкой пластмассы. При каждом перескакивании с витка на виток она будет издавать отчетливый щелчок. Достаточно сосчитать количество этих щелчков и прибавить к ним единицу (с последнего витка полоска соскочит почти беззвучно, поскольку не ударится о следующий).

Умножьте длину окружности одного витка пружины на число витков:L=lN, где L — длина проволоки, из которой свита пружина, мм, l — длина окружности одного витка, мм, N — количество витков пружины (безразмерная величина).

Обратите внимание

При необходимости используйте защитные перчатки. Сжимайте и разжимайте пружину не резко, а плавно. Защищайте глаза.

Полезный совет

Сжимая сильную пружину, будьте осторожны — она может выскользнуть и причинить травмы. Очень сильные пружины лучше измерять в разжатом или слегка сжатом состоянии, несмотря на то, что точность при этом несколько уменьшится. Особенно осторожным нужно быть, если для сжатия используются тиски или другие механические приспособления.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Евлампий

4 декабря, 16:07

+1

Дано:

m = 200 г = 0,2 кг

k = 1000 Н/м

Найти:

L

F = kL

mg = kL

L = mg / k

L = 0,2 • 10 / 1000 = 0,002 м = 2 мм

Ответ: 2 мм
- Комментировать
- Жалоба
- Ссылка

Найди верный ответ на вопрос ✅ «Найти удлинение пружины, возникающее под действием подвешенного к ней груза массой 200 г, если жесткость пружины равна 1000 Н/м …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » Физика » Найти удлинение пружины, возникающее под действием подвешенного к ней груза массой 200 г, если жесткость пружины равна 1000 Н/м

Источник

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

сдвиг;
кручение;
изгиб;
сжатие/растяжение;

Рис. 1. пластиковая линейка, деформированная изгибом – а) и кручением – б)

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Расчет силы упругости

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

[ large boxed{ F_{text{упр}} = k cdot Delta L }]

Эту формулу назвали законом упругости Гука.

( F_{text{упр}} left( H right) ) – сила упругости;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

[ large F_{text{упр}} — m cdot g = 0 ]

Подставим в это уравнение выражение для силы упругости

[ large k cdot Delta L — m cdot g = 0 ]

[ large boxed{ k = frac{ m cdot g }{Delta L} }]

(g) – ускорение свободного падения, оно связано с силой тяжести.

Расчет винтовых цилиндрических одножильных пружин растяжения и сжатия.

Рассмотрим расчет винтовых цилиндрических одножильных пружин растяжения и сжатия. Основные геометрические параметры винтовых цилиндрических пружин из проволоки круглого поперечного сечения (см. рис. 1): d — диаметр проволоки; Dн и D — наружный и средний диаметры пружины; c=D/d — индекс пружины; t — шаг пружины; α — угол подъема витков; L0 — длина развернутой пружины (без учета зацепов пружины). Податливость пружины прямо пропорциональна ее индексу c. Для увеличения податливости пружины индекс с принимают возможно большим; практически c=4…12.
Значения индекса с пружины принимают в зависимости от диаметра проволоки:

d, мм	< 2,5	3…5	6…12
c	5…12	4…10	4…9

Рис. 1
С увеличением индекса пружины той же жесткости можно сократить ее длину путем увеличения диаметра, а с уменьшением индекса можно уменьшить диаметр пружины путем увеличения ее длины.
Рис. 2
В любом поперечном сечении витка пружины растяжения или сжатия при работе возникают (рис. 2, а) сила F, направленная по осевой линии пружины, и момент М=FD/2, вектор которого перпендикулярен осевой линии пружины. Сила F раскладывается на поперечную F1=F cos α и продольную F2=F sin α силы. При разложении момента М по осевой линии витка пружины и перпендикулярному ему направлению в поперечном сечении проволоки пружины возникают: крутящий T=FD cos α/2 и изгибающий Ми=FD sin α/2 моменты. Так как угол α<10…12°, то изгибающий момент Ми значительно меньше крутящего Т, а продольная сила F2 значительно меньше поперечной силы F1 но, как показывают расчеты, касательные напряжения сдвига значительно меньше касательных напряжений кручения, поэтому для упрощения расчета пружин на прочность обычно учитывают лишь крутящий момент T, при этом приближенно принимают cos α=1, т. е. T=М=FD/2. Таким образом, расчет винтовой цилиндрической пружины растяжения или сжатия из проволоки круглого поперечного сечения производят по формуле

где τ — расчетное максимальное напряжение в поперечных сечениях витков пружины; [τ] — допускаемое напряжение для проволоки пружины; k — коэффициент влияния на напряжение кривизны витков и поперечной силы; F — максимальная растягивающая или сжимающая сила. Формулой пользуются при проверочном расчете пружины, когда ее размеры известны.
Значения коэффициента k принимают в зависимости от индекса пружины:

c	4	5	6	8	10	12
k	1,37	1,29	1,24	1,17	1,14	1,11

Рис. 3
Допускаемое напряжение [τ] пружин при статических нагрузках можно принимать по графикам (рис. 3), где отдельные кривые относятся к пружинам из проволоки:

1 — вольфрамовой и рояльной;
2 — хромованадиевой;
3 — углеродистой, закаленной в масле;
4 — углеродистой холоднотянутой;
5 — моиель-металла;
6 — фосфористой бронзы;
7 — специальной латуни.

При пульсирующей нагрузке с небольшим числом циклов допускаемые напряжения [τ] следует принимать в 1,25…1,5 раза ниже, чем по графикам.

При проектировочном расчете пружины диаметр проволоки

значением индекса с пружины задаются. Диаметр d проволоки, вычисленный по формуле, окончательно согласовывают с соответствующим ГОСТом для пружинной проволоки.

Средний диаметр D пружины и наружный диаметр DH определяют по формулам

При расчетах различают следующие силы пружины (см. рис. 1 , а, б): при предварительной деформации — F1 при рабочей деформации (соответствует наибольшему принудительному перемещению подвижного звена в механизме) — F2; при максимальной деформации «(допускаемой) — F3. Соответственно в формулах F=F3.

Обычно пружину устанавливают с действующей на нее начальной нагрузкой F1=(0,1…0,5)F2. Максимальная сила пружины F3=(1,05..,1,66)F2. При изменении силы пружины от F1 до F2 жесткость пружины

где h — рабочий ход пружины, значение которого назначают или вычисляют по условиям работы механизма. Жесткость одного витка пружины где G — модуль сдвига материала проволоки пружины. Для стали G=80000 МПа и, следовательно, для стальной пружины где С1 — в Н/мм; d — в мм.

Число рабочих витков пружины

Полное число витков

где n2=1,5…2 — число опорных витков.

Деформация пружины

Подставив в формулу вместо F силы F1, F2, F3, получим деформации: λ1 — предварительную, λ2 — рабочую и λ3 — максимальную. Максимальная деформация одного витка пружины

Шаг пружины в ненагруженном состоянии: для пружины сжатия
для пружины растяжения
Высота пружины при максимальной деформации

где n3 — число зашлифованных витков. Высота пружины в свободном состоянии для пружины сжатия для пружины растяжения

Высоту пружины при предварительной и рабочей деформации легко определить из (рис. 1, а, б). Длина развернутой пружины (без учета зацепов пружины растяжения)

Более подробный геометрический расчет винтовых цилиндрических пружин сжатия и растяжения из стальной проволоки круглого сечения дан в ГОСТ 13765-68.

Соединяем две одинаковые пружины

Параллельное соединение пружин

Рис. 5. Две пружины, соединенные параллельно, деформируются меньше одной такой пружины

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две параллельные пружины:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{параллел}} cdot Delta L cdot frac{1}{2}= k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

[ large k_{text{параллел}} cdot frac{1}{2}= k_{1} ]

Умножим обе части полученного уравнения на число 2:

[ large boxed{ k_{text{параллел}} = 2k_{1} } ]

Коэффициент жесткости (k_{text{параллел}}) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Одна пружина:

[ large k_{1} cdot Delta L = m cdot g ]

Две последовательные пружины:

[ large k_{text{послед}} cdot Delta L cdot 2 = m cdot g ]

Так как правые части уравнений совпадают, левые части тоже будут равны:

[ large k_{text{послед}} cdot Delta L cdot 2 = k_{1} cdot Delta L ]

Обе части уравнения содержат величину (Delta L ). Разделим обе части уравнения на нее:

Not Found

Пример

1. Пружина сжатия. Дано: F1 = 20 Н; F2 = 80Н; h = 30мм; D1 = 10÷
12мм; Vmax = 5 м/с; NF ≥ 1∙107. Пользуясь табл. 1, убеждаемся, что при заданной выносливости пружину следует отнести к классу I. По формуле (2), пользуясь интервалом значений 8 от 0,05 до 0,25 (формула (1)], находим граничные значения силы F3, a именно:
F3 = F2/(1-0,05) ÷ F2/(1-0,25)=84 ÷ 107 Н

В интервале от 84 до 107 Н (ГОСТ 13766—86) пружин класса I, разряда 1 имеются следующие силы F3 ; 85; 90; 95; 100 и 106 Н (табл. 11). Исходя из заданных размеров диаметра и стремления обеспечить наибольшую критическую скорость, останавливаемся на витке со следующими данными (номер позиции 355): F3 = 106 H; d = 1,80 мм; D1 = 12 мм; с1 =97,05 Н/мм; s′3 = 1,092 мм. Учитывая, что для пружин класса I норма напряжений τ = 0,3Rm (см. табл. 2), находим, что для найденного диаметра проволоки из углеродистой холоднотянутой стали расчетное напряжение τ33 ≈ 0,3 · 2100 = = 630 Н/мм2. Принадлежность к классу I проверяем путем определения отношения vmax / vk , для чего предварительно определяем критическую скорость по формуле (5)при d = 0,25:

Полученная величина указывает на отсутствие соударения витков, и, следовательно, выбранная пружина удовлетворяет заданным условиям, но так как пружины класса II относятся к разряду ограниченной выносливости, то следует учитывать комплектацию машины запасными пружинами с учетом опытных данных. Определение остальных размеров производим по формулам табл. 10. По формуле (6) находим жесткость пружины c = (F2-F1)/h= (80-20)/30=2.0 Н/мм. Число рабочих витков пружины определяем по формуле (7): n = c1/c = 36,58/2,0 = 18,29 ≈ 18,5 Уточненная жесткость имеет значение c = c1/n = 36,58/18,5= 1,977 ≈ 2,0 Н/мм. При полутора нерабочих витках полное число витков находим по формуле (8): n1 = n + n2 = 18,5 + 1,5 = 20 По формуле (9) определяем средний диаметр пружины D =

11,5 — 1,40 = 10,1 мм. Деформации, длины и шаг пружины вычисляем по формулам [(11)-(18)]:

На этом определение размеров пружины и габарита узла (размер ℓ1) заканчивается. Следует отметить, что некоторое увеличение выносливости может быть достигнуто при использовании пружины с большей величиной силы F3 , чем найденная в настоящем примере. С целью выяснения габаритов, занимаемых такой пружиной, проделаем добавочный анализ: остановимся, например, на витке со следующими данными по ГОСТ 13770-86 (позиция 313); F3 = 106 H; d = 1,4 мм; D1 = 10,5 мм; с1 =50,01 Н/мм; s′3 = 2,119 мм. Находим τ = 1150 Н/мм2 и производим расчет в той же последовательности: d = 1- (F2/F3)=1- (80/106) = 0,245; vk= (1150 · 0,245) /35,1 = 8,05 м/с, vmax / vk = 5,0/8,05 =0,622 Очевидно, что у этой пружины создается большой запас на несоударяемость витков. Далее в рассмотренном ранее порядке находим n=50,01/2,0= 25,01 ≈ 25,0 Уточненная жесткость с =50,01/25,0

≈ 2,0 Н/мм;

Таким образом, устанавливаем, что применение пружины с более высокой силой F3

хотя и привело к большему запасу на несоударяемость витков, но оно сопровождается увеличением габарита узла (размер ℓ1) на 15,3 мм. Можно показать, что если выбрать виток с большим диаметром, например D1 = 16 мм (ГОСТ 13770-86, номер позиции 314), то тогда потребуется расширить узел по диаметру, но при этом соответственно уменьшится размер ℓ1.

Пример 2. Пружина сжатия. Дано: F1 = 100 Н; F2 =

250 Н; h
=
100 мм; D1 = 15 ÷ 25 мм; vmax = 10 м/с Независимо от заданной выносливости на основании формулы (5) можно убедиться, что при значениях d, меньших 0,25 [формула (1)], все одножильные пружины, нагружаемые со скоростью vmax более 9,4 м/с, относятся к III классу. По формуле (2) с учетом диапазона значений d для пружин класса III от 0,1 до 0,4 [формула (1)] находим границы сил
;
F3=F2/(1-0,1)÷ F2/(1-0,4) = 250/0,9 ÷ 250/0,6 =278÷417 Н Верхние значения силы F3
,
как видно из табл. 2 ГОСТ 13764—86, не могут быть получены из числа одножильных конструкций, поэтому, учитывая коэффициенты d = 0,15 ÷ 0,40 [формула (1)] для трехжильных пружин, устанавливаем новые пределы F3, по формуле (2): F3
=
294÷417 Н. Для указанного интервала в ГОСТ 13774-86 имеются витки со следующими силами
F3:
300; 315; 335; 375 и 400 (табл. 16а). Исходя из заданных размеров диаметра и наименьших габаритов узла, предварительно останавливаемся на витке со следующими данными (номер позиции 251): F3 = 300 Н; d = 1,4 мм; d1
=
3,10 ; D1
=
17 мм; с1 = 50,93 Н/мм; s′3= 5,900 мм. Согласно ГОСТ 13764—86 для пружин класса III τ3 = 0,6 Rm
.
Используя ГОСТ 9389-75, определяем напряжение для найденного диаметра проволоки τ3 = 0,6 · 2300 = 1380 МПа. Принадлежность к классу проверяем путем определения величины отношения vmax / vk для чего предварительно находим d и критическую скорость по формулам (1), (2) и (5а): d = 1-(F2/F3) = 1-(250/300)= 0,167; vk= (1380 · 0,167)/32,4 = 7 м/с vmax / vk= 10,0 /7,0=1,43 > 1. Полученное неравенство свидетельствует о наличии соударения витков и о принадлежности пружины к классу III. Определение остальных параметров производится по формулам табл. 10. По формуле (6) находим жесткость c = (F2- F1) / h = 250-100/100= 1,5 Н/мм. Число рабочих витков пружины вычисляют по формуле (7): n = c1/c = 50,9/1,5 = 33,9 ≈ 34,0 Уточненная жесткость
с
= c1 /n = 50,9/34,0 = 1,49 ≈ 1,5 Н/мм. Полное число витков находят по формуле (8): n1 = n + 1,5 = 34,0 + 1,5 = 35,5 . По формуле (9а) определяют средний диаметр пружины D
=
D1 — d1
=
17 — 3,10 = 13,90 мм. Деформации, длины и шаг пружины находят по формулам в табл. 10 [формулы (10а), (11)-(18а)]: s1 = F1/c = 100/1,5 = 66,7 мм; s2 = F2/c = 250/1,5 = 166,7 мм; s3 = F3/c = 300/1,5 =200 мм ; i = D/d1=13,90/3,10 =4,5; ℓ3
= (n1+1) d1∆ = (35,5 + 1) 3,10 · 1,021 = 115,5 мм; ℓ0=
ℓ3 + s3 = 115,5 + 200 = 315,5 мм; ℓ1 =ℓ0 — s1 = 315,5 — 66,7 = 248,8 мм; ℓ2 =ℓ0 — s2
=
315,5 — 166,7 = 148,8 мм
t
= s’3
+
d1∆ = 5,9 + 3,10 · 1,021 = 9,19 мм.Проанализируем пружины, соответствующие трем ближайшим значениям F3
,
взятым из ГОСТ 13774—86 (пружины класса III, разряда 1) для рассмотренного случая (табл. 16а). Вычисления, проделанные в аналогичном порядке, показывают, что для трех соседних сил F3 образуется шесть размеров пружин, удовлетворяющих требованиям по величине наружного диаметра. Сведения о таких пружинах приведены ниже.

F3,H	300	315	335
d , мм	1,4	1,6	1,4	1,6	1,4	1,6
d1 , мм	3,10	3,50	3,10	3,50	3,10	3,50
D1 , мм	17,0	24,0	16,0	22,0	15,0	21,0
vmax / vk	1,43	1,50	1,16	1,21	0,942	0,984
ℓ0, мм	317,0	273,9	355,1	309,0	405,1	337,0
ℓ1, мм	250,4	207,2	288,4	242,3	338,4	270,3
ℓ2, мм	150,4	107,2	188,4	142,3	238,4	170,3
n1, мм	36,0	20,0	44,5	27,0	56,0	31,0
V,мм3	57000	93000	58000	92000	60000	93000

Из этих данных следует, что с возрастанием F3 уменьшается отношение vmax / vk и, в частности, может быть устранено соударение витков, но вместе с этим возрастают габариты по размерам ℓ1. С возрастанием диаметров пружин габариты по размерам ℓ1 уменьшаются, однако существенно возрастают объемы пространств, занимаемые пружинами. Следует отметить, что если бы для рассматриваемого примера, в соответствии с требованиями распространенных классификаций, была выбрана пружина класса I, то при одинаковом диаметре гнезда (

D1 ≈ 18 мм) даже самая экономная из них потребовала бы длину гнезда ℓ1 = 546 мм, т. е. в 2,2 раза больше, чем рассмотренная выше. При этом она была бы в 11,5 раза тяжелее и, вследствие малой критической скорости (vk = 0,7 м/с), практически неработоспособной при заданной скорости нагружения 10 м/с.

Пример

3. Пружина растяжения. Дано: F1 = 250 Н; F2 = 800 Н; h = 100 мм; D1 = 28 ÷ 32 мм; NF ≥ 1· 105.На основании ГОСТ 13764—86 по величине
NF
устанавливаем, что пружина относится к классу II (см. табл. 1.) По формуле (2) находим силы
F3
, cоответствующие предельной деформации: F3 = F2/(1-0,05) ÷ F2/(1-0,10) =842÷ 889 Н. В интервале сил 842—889 Н в ГОСТ 13770—86 для пружин класса II, разряда 1 (номер пружины 494) имеется виток со следующими параметрами: F3 = 850 Н; D1
=
30 мм; d = 4,5 мм; с1 = 242,2 Н/мм; s’3 =3,510 мм (см. табл. 14). По заданным параметрам с помощью формулы (6) определяем жесткость пружины:
с = (
F2- F1)/h = (800-250)/100 = 5,5 H/мм. Число рабочих витков находим по формуле (7): n = c1/c = 242,2 / 5,5 ≈ 44.Деформации и длины пружины вычисляют по формулам [(11)-(17а)]: s1=F1/c = 250/5,5 =45,5 мм; s2 = F2/c = 800/5,5 = 145,5 мм; s3 = F3/c = 850/5,5 = 154,5 мм ; ℓ’0
=
(n +1)d= (44+1)4,5 = 202,5 мм; ℓ1 =ℓ0 + s1 = 202,5 + 45,5 = 248,0 мм; ℓ2 =ℓ0 + s2
=
202,5 +145,5 = 348,0 мм; ℓ3 =ℓ0 + s3
=
202,5 +154,5 = 357,0 мм. Размер ℓ2 с учетом конструкций зацепов определяет длину гнезда для размещения пружины растяжения в узле. Размер ℓ3 с учетом конструкций зацепов ограничивает деформацию пружины растяжения при заневоливании. Трехжильные пружины (угол свивки 24º). Жесткость s1=F1/s1 = F2/s2 =F3/s3 = 30000d4k/D3n = H/мм; k= (1+ 0,333· sin22b)/ cosb b = arctg (0,445 i / i+1) , i = D/d1Напряжение τ3 = 1,82 F3 i /d2МПа Полученные значения жесткости должны совпадать с вычисленными по формуле (6). Полученные значения напряжений должны совпадать с указанными в ГОСТ 13764—86 для соответствующих разрядов с отклонениями не более + 10
%.
404 Not Found

The requested URL /bottom.php was not found on this server.

Additionally, a 404 Not Found error was encountered while trying to use an ErrorDocument to handle the request.

Потенциальная энергия сжатой или растянутой пружины

Рис. 7. Деформированная — сжатая или растянутая пружина обладает потенциальной энергией

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

[ large boxed{ E_{p} = frac{k}{2} cdot left( Delta L right)^{2} }]

( E_{p} left( text{Дж} right)) – потенциальная энергия сжатой или растянутой пружины;

( Delta L left(text{м} right) ) – удлинение пружины;

( displaystyle k left(frac{H}{text{м}} right) ) – коэффициент жесткости (упругости) пружины.

Плоские спиральные пружины

Плоские спиральные пружины изготавливают из тонкой высококачественной углеродистой ленты. Применяют в качестве заводных, аккумулирующих энергию, что возможно благодаря высокой гибкости ленты, позволяющей иметь большой угол поворота валика до нескольких десятков оборотов. Пружины обычно помещают в барабан для обеспечения смазки и придания им определённых внешних размеров. В неответственныхмеханизмах используютспиральные пружины и без барабанов. Внутренний конец пружины крепят, как правило, к валику, а наружный к барабану.

КПД спиральных пружин определяется отношением работы, производимой пружиной при развёртывании к работе, затрачиваемой на заводку, и колеблется в пределах 0,6-0,7 в зависимости от смазки. Следует избегатьпружин повышенной толщины ленты, так как они работают не плавно, что ведёт к перенапряжению в материале пружины и к её поломке. Толщину ленты пружины b

следует выбирать из условия
, , где r
–
радиусвалика, на который наматывается пружина. Уравнение оси пружиннойленты, плотно навитой на валик, в полярных координатах ,где ρ–текущий полярный радиус, φ- полярный угол. Начальный радиус ρ1 соответствует углу φ1.Конечный радиус ρ2 соответствуетуглуφ2 = φ1 +2n, где n—число оборотов спирали пружины равное .
Рабочая длина ленты пружиныL

= .

При жёстком закреплении концов пружины в корпусе и на валике, она испытывает чистый изгиб. Напряжение изгиба ленты ,где h

–
высота ленты, М
– изгибающиймомент. Отсюда требуемая высота ленты
.
Суммарный угол закручивания ,где J

– момент инерции сечения ленты.

Максимальный момент на валике пружины ,где nр

– максимальное расчётноечисло витков пружины.
nр =n2 – n1 , где n2
– число витков заведенной пружины в барабане, n1 – число витков свободной пружины (вне барабана).

Рабочее число оборотов барабанаφпри расчёте следует увеличивать на 0,5-1,5 для покрытия потерь на трение.

Минимальный момент на валике пружины , где np.min = n – n1 ; n –число витков спущенной пружины (в барабане).

Тарельчатые пружины

выбирают равным 2-3, а угол подъема образующей конуса 2-60. В соответствии с ГОСТ 3957 тарельчатые пружины выполняют наружным диаметром 28-300мм, толщиной
s = 1-20мм
, высотой конуса
f= 0,6-9мм
. Рабочая нагрузка пружин до 520 кН. Упругая осадка пружин допускается до 0,8f.

Тарельчатые пружины, имея небольшие габариты по высоте, представляют значительные преимущества по сравнению с другими пружинами для больших нагрузок при высокой потребной жёсткости, что и определяет область их применения. На рис. б показано обычное выполнение пакета пружин для максимальной податливости. На рис. в

показан пакет с тройным набором односторонних пружин для повышения несущей способности. На рис.
г
пакет пружин с промежуточными шайбами, более активно демпфирующих энергию колебаний.

Тарельчатые пружины штампуют, как правило, из листовой кремнистой стали 60С2А. Для повышения несущей способности их обжимают пере закалкой до полного распрямления, в результате чего в них возникают остаточные напряжения обратного знака.

Точный расчёт пружин довольно сложен и их обычно подбирают по таблицам ГОСТа 3957.

Приближённая зависимость между осевой силой Р

и осевым сжатием
λ1
одного элемента пружины , где
E и μ
– модуль упругости и коэффициент Пуассона материала пружины;

– коэффициент, принимаемый по приведенному графику.

Наибольшее напряжение сжатия на внутренней кромке пружины .

Коэффициенты К, К0, К1

также принимают по графику. Допускаемые напряжения по приведенной формуле выбирают весьма высокими, достигающими при статической нагрузке для кремнистой стали
1600 – 2000 МПа
.

Выводы

Упругие тела – такие, которые сопротивляются деформации;
Во время деформации в упругих телах возникает сила, она препятствует деформации, ее называют силой упругости;
Деформация – изменение формы, или размеров тела;
Есть несколько видов деформации: изгиб, кручение, сдвиг, растяжение/сжатие;
Удлинение пружины – это разность ее конечной и начальной длин;
Сжатая или растянутая пружина обладает потенциальной энергией (вообще, любое упруго деформированное тело обладает потенциальной энергией);
Система, состоящая из нескольких одинаковых пружин, будет иметь коэффициент жесткости, отличный от жесткости единственной пружины;
Если пружины соединяют параллельно – коэффициент жесткости системы увеличивается;
А если соединить пружины последовательно – коэффициент жесткости системы уменьшится.

Источник

Содержание

Определение и формула жесткости пружины
Формула жесткости соединений пружин
Примеры задач с решением
Типы пружин
Физические характеристики пружин
Понятие жесткости
Расчет жесткости цилиндрической пружины

Определение и формула жесткости пружины

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости.

Чаще всего ее обозначают $<overline>_$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

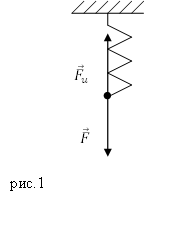
Рассмотрим пружину, на которую действует растягивающая сила ($overline$), которая направлена вертикально вниз (рис.1).

Силу $overline$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости ($<overline>_u$), уравновешивающая силу $overline$. Если деформация является небольшой и упругой, то удлинение пружины ($Delta l$) прямо пропорционально деформирующей силе:

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) — это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости — это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ — модуль сдвига (величина, зависящая от материала); $d$ — диаметр проволоки; $d_p$ — диаметр витка пружины; $n$ — количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.

Формула жесткости соединений пружин

Пусть $N$ пружин соединены последовательно. Тогда жесткость всего соединения равна:

где $k_i$ — жесткость $i-ой$ пружины.

При последовательном соединении пружин жесткость системы определяют как:

Примеры задач с решением

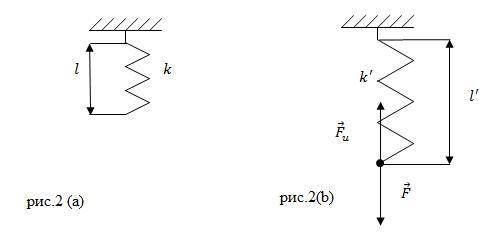
Задание. Пружина в отсутствии нагрузки имеет длину $l=0,01$ м и жесткость равную 10 $frac<Н><м>. $Чему будет равна жесткость пружины и ее длина, если на пружину действовать силой $F$= 2 Н? Считайте деформацию пружины малой и упругой.

Решение. Жесткость пружины при упругих деформациях является постоянной величиной, значит, в нашей задаче:

При упругих деформациях выполняется закон Гука:

[F=kDelta l left(1.2
ight).]

Из (1.2) найдем удлинение пружины:

Длина растянутой пружины равна:

Вычислим новую длину пружины:

Ответ. 1) $k’=10 frac<Н><м>$; 2) $l’=0,21$ м

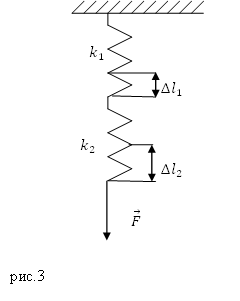
Задание. Две пружины, имеющие жесткости $k_1$ и $k_2$ соединили последовательно. Какой будет удлинение первой пружины (рис.3), если длина второй пружины увеличилась на величину $Delta l_2$?

Решение. Если пружины соединены последовательно, то деформирующая сила ($overline$), действующая на каждую из пружин одинакова, то есть можно записать для первой пружины:

Для второй пружины запишем:

Если равны левые части выражений (2.1) и (2.2), то можно приравнять и правые части:

[k_1Delta l_1=k_2Delta l_2left(2.3
ight).]

Из равенства (2.3) получим удлинение первой пружины:

Ответ. $Delta l_1=frac$

Недеформированная пружина жесткостью К, укрепленная на гладком горизонтальном стержне, имеет длину l. На свободном конце пружины закрепили шарик массой m. При вращении системы с угловой скоростью w (амега) шарик растягивает пружину. Найти длину пружины при вращении.

Как вывести формулу l=kl1/k-mw^2 для этой задачи??

Пружина — упругий объект, целенаправленно подвергающийся сжатию или растяжению, в результате чего может запасать энергию, а затем, при ослабевании внешней деформирующей силы, возвращать ее. Пружины в нормальных условиях не должны подвергаться остаточным (пластическим) деформациям, т.е. таким воздействиям, после которых форма изделия уже не восстанавливается вследствие нарушения структуры их материала.

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.

Попробуй обратиться за помощью к преподавателям

Физические характеристики пружин

Цилиндрические пружины характеризуются рядом параметров, сочетание которых обуславливает их жесткость — способность сопротивляться деформации:

материал; пружины чаще всего изготавливают из стальной проволоки, причем сталь в них применялася особая, ее характеризует среднее или высокое содержание углерода, низкое содержание других примесей (низколегированный сплав) и особая термообработка (закалка), придающая материалу дополнительную упругость;
диаметр проволоки; чем он меньше, тем эластичнее пружина, но тем меньше ее способность запасать энергию; пружины сжатия изготавливают, как правило, из более толстой проволоки, чем пружины растяжения;
форма сечения проволоки; не всегда проволока, из которой намотана пружина, имеет круглое сечение; уплощенное сечение имеют пружины сжатия, чтобы при максимальном сокращении длины (виток «садится» на соседний виток) конструкция была более устойчивой;
длина и диаметр пружины; длину пружины следует отличать от длины проволоки, из которой она намотана; эти два параметра согласуются через количество витков и диаметр пружины, который, в свою очередь, не следует путать с диаметром проволоки.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Существуют и другие физические характеристики, влияющие на работоспособность пружин. Например, при повышении температуры металл становится менее упругим, а при существенном ее понижении может стать хрупким. При интенсивной эксплуатации пружина со временем теряет часть упругости по причине постепенного разрушения связей между атомами кристаллической решетки.

Понятие жесткости

Жесткость как физическая величина характеризует силу, которую нужно приложить к пружине для достижения определенной степени растяжения или сжатия.

Коэффициент жесткости рассчитывается по формуле Гука:

где $F$ — сила, развиваемая пружиной, $k$ — коэффициент жесткости, зависящий от ее характеристик (см. выше) и измеряемый в ньютонах на метр, $x$ — абсолютное приращение расстояния, на которое изменилась длина пружины после приложения внешней силы. Знак минус в правой части формулы свидетельствует о том, что сила, порождаемая пружиной, действует в противоположном по отношению к нагрузке направлении.

Коэффициент жесткости можно вычислить экспериментально, подвешивая на расположенную вертикально и закрепленную за верхний конец пружину грузы с известной массой. В этом случае имеет место зависимость

$m cdot g — k cdot x = 0$,

где $m$ — масса, $g$ — ускорение свободного падения. Отсюда

Расчет жесткости цилиндрической пружины

Довольно просто понять как работает плоская пружина. Если положить на край письменного стола линейку и прижать один ее конец рукой к поверхности, но второй можно упруго изгибать, запасая и высвобождая энергию. Очевидно, что в момент изгиба расстояния между молекулами материала в некоторых фрагментах линейки увеличиваются, в некоторых уменьшаются. Электромагнитные связи, действующие между молекулами, стремятся вернуть вещество к прежнему геометрическому состоянию.

Несколько сложнее дело обстоит с цилиндрической пружиной. В ней энергия запасается не благодаря деформации изгиба, а за счет скручивания проволоки, из которой пружина навита, относительно продольной оси этой проволоки.

Представим сильно увеличенное сечение проволоки, из которой навита цилиндрическая пружина, выполненное перпендикулярной ее оси плоскостью. При таком рассмотрении можно абстрагироваться от спиральной формы и мысленно разбить весь объем проволоки на множество соприкасающихся торцевыми поверхностями «цилиндров», диаметр которых равен диаметру проволоки, а высота стремится к нулю. Между соприкасающимися торцами действуют молекулярные силы, препятствующие деформации.

При растяжении или сжатии пружины угол наклона между витками изменяется. Соседние «цилиндры» при этом вращаются друг относительно друга в противоположных направлениях вокруг общей оси. В каждом таком сечении запасается энергия. Отсюда следует, что чем из более длинного куска проволоки навита пружина (здесь играют роль диаметр и высота цилиндра, а также шаг витка), тем большее количество энергии она способна запасти. Увеличение диаметра проволоки также повышает ее энергоемкость. В целом формула, учитывающая основные факторы жесткости пружины, выглядит так:

$R$ — радиус цилиндра пружины,
$n$ — количество витков проволоки радиуса $r$,
$G$ — коэффициент, зависящий от материала.

Рассчитать коэффициент жесткости пружины, выполненной из стальной проволоки с $G = 8 cdot 10^<10>$ Па и диаметром 1 мм. Радиус пружины 20 мм, количество витков — 25.

Подставим в формулу числовые значения, попутно переведя их в единицы системы СИ:

Ответ: $100 frac<Н><м>$

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Источник