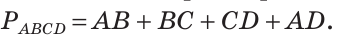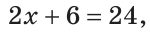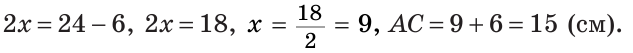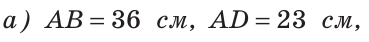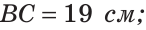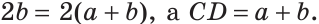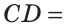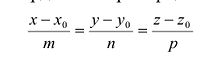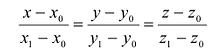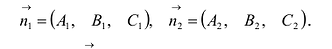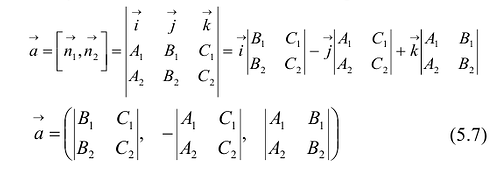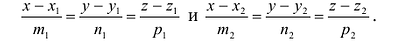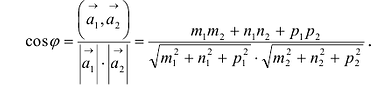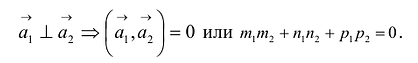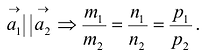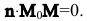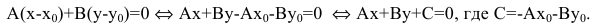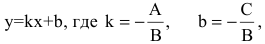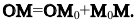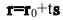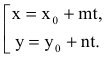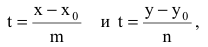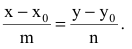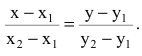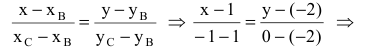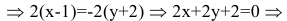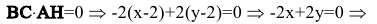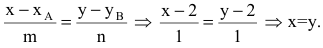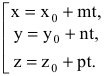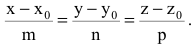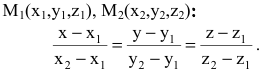• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных
Уравнение прямой по точке и вектору нормали.
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В)
перпендикулярен прямой , заданной уравнением
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С
подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно
С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки.
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой,
проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На
плоскости записанное выше уравнение прямой упрощается:
Дробь = k называется угловым коэффициентом прямой.
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту.
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить , то полученное уравнение называется
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору.
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание
прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор (α1, α2), компоненты которого удовлетворяют условию
Аα1 + Вα2 = 0 называется направляющим вектором прямой.
Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением,
коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.
при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
Уравнение прямой в отрезках.
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
или , где
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения
прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, , а = -1, b = 1.
Нормальное уравнение прямой.
Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется
нормирующем множителем, то получим
xcosφ + ysinφ — p = 0 – нормальное уравнение прямой.
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = < l , m >- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 |
x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
http://ru.onlinemschool.com/math/library/analytic_geometry/line/

Уравнением линии на плоскости называется уравнение F(x, y) = 0, ко-
торому удовлетворяют координаты любой точки данной линии и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Другими словами, линия, определенная данным уравнением (в некоторой системе координат), есть геометрическое место всех точек плоскости, координаты которых удовлетворяют этому уравнению.
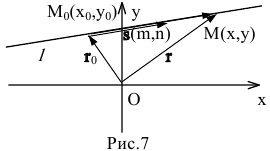
Прямая линия в векторной форме может быть задана уравнением
|
n ×( r –r0 )=0, |
(3.8) |
|
где n = (A; B) – вектор, перпендикулярный прямой; |
r = (x; y) – радиус-вектор |
произвольной точки прямой; r0 = (x0 ; y0 ) – радиус-вектор фиксированной точки прямой.
Любая прямая на плоскости может быть задана в фиксированной декартовой прямоугольной системе координат уравнением первой степени. Обратно, любое уравнение первой степени относительно декартовых координат является уравнением прямой. Уравнение вида
называется общим уравнением прямой. В уравнении (3.9) числа A, B,C – постоянные, причем A и B не равны нулю одновременно.
Если в общем уравнении прямой (3.9) один или два из трех коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным.
Если ни один из коэффициентов уравнения (3.9) не равен нулю, то его можно преобразовать к виду
|
x |
+ |
y |
= 1, |
(3.10) |
|
|
a |
b |
||||
где a = — CA и b = — CB есть величины отрезков, которые отсекает прямая на ко-
ординатных осях. Каждый из этих отрезков отложен от начала координат. Уравнение (3.10) называется уравнением прямой «в отрезках». Расстояние от точки P(x0 ; y0 ) до прямой (3.9) находится по формуле
|
d = |
Ax0 |
+ By0 |
+ C |
. |
(3.11) |
||
|
A2 + B2 |
|||||||
Угол a , определяемый, как показано на рис. 3.5, называется углом наклона прямой к оси Ох (0 £ a < p ) .
91

Рис. 3.5
Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; обычно его обозначают буквой k:
|
k=tga . |
(3.12) |
|
Уравнение вида |
|
|
y=kx+b |
(3.13) |
называется уравнением прямой с угловым коэффициентом;
k — угловой коэффициент, b — величина направленного отрезка, который отсекает прямая на оси Оу, считая от начала координат.
Если прямая задана общим уравнением Ах+Ву+С=0, то ее угловой коэф-
фициент определяется по формуле k= — BA , (B ¹ 0).
Уравнение
|
y — y0 = k(x — x0 ) |
(3.14) |
является уравнением прямой, которая проходит через точку P(х0; у0) и имеет угловой коэффициент k.
Если прямая, проходящая через заданную точку Q(x1; y1 ) , параллельна оси Oy , то ее уравнение имеет вид
|
x = x1. |
(3.15) |
|
Если прямая, проходящая через заданную точку Q(x1; y1 ) , параллельна |
|
|
оси Ox , то ее уравнение имеет вид |
|
|
y = y1 . |
(3.16) |
Если k – заданное число, то уравнение (3.14) представляет вполне определенную прямую, если же k – переменный параметр, то это уравнение определит пучок прямых, проходящих через точку P(x0 ; y0 ) (рис. 3.6), при этом
k называется параметром пучка.
92

Если прямая проходит через точки M1(x1; у1) и М2(х2; у2), то из рис. 3.7 ее угловой коэффициент определяется по формуле
|
k = |
y2 — y1 |
. |
(3.17) |
||||
|
x |
— x |
||||||
|
2 |
1 |
||||||
|
Уравнение |
|||||||
|
x — x1 |
= |
y — y1 |
(3.18) |
||||
|
x |
— x |
||||||
|
y |
2 |
— x |
|||||
|
2 |
1 |
1 |
описывает прямую, проходящую через две точки М1(x1; y1) и M2(x2; у2).
Совместное исследование уравнений прямых
Рассмотрим систему двух линейных уравнений с двумя неизвестными x и y :
|
ìA1x + B1 y + C1 |
= 0, |
(3.19) |
|
í |
||
|
îA2 x + B2 y + C2 |
= 0. |
Каждое уравнение системы (3.19) определяет некоторую прямую. Вопрос о существовании и количестве вещественных решений системы (3.19) равносилен вопросу о существовании и количестве общих точек этих прямых. Возможны три случая.
1.Прямые пересекаются, т.е. имеют единственную общую точку – система (3.19) имеет единственное решение. Критерием пересечения двух прямых
является условие A1 ¹ B1 .
A2 B2
2. Прямые совпадают, т.е. оба уравнения системы определяют одну и ту же прямую – система (3.19) имеет бесконечное множество решений. Крите-
рием совпадения двух прямых является условие A1 = B1 = C1 .
A2 B2 C2
3. Прямые параллельны – система (3.19) не имеет решений. Критерием па-
раллельности двух прямых является условие A1 = B1 ¹ C1 .
A2 B2 C2
В случае если две прямые (3.19) пересекаются, то один из двух смежных углов φ, образованных при пересечении этих прямых, определяется по формуле
93

|
tgj = |
A1B2 |
— A2 B1 |
. |
(3.20) |
||
|
A A |
||||||
|
+ B B |
||||||
|
1 |
2 |
1 |
2 |
Если известны угловые коэффициенты двух прямых k1 и k2, то угол φ от первой прямой до второй, отсчитываемый против хода часовой стрелки определяется по формуле
|
tgj = |
k2 — k1 |
. |
(3.21) |
||
|
1 |
+ k k |
2 |
|||
|
1 |
Условием параллельности двух прямых является равенство их угловых коэффициентов
Условием перпендикулярности двух прямых является соотношение
|
k1k2=–1 или k2= – |
1 |
. |
(3.23) |
k1
Если три прямые A1x+B1y+С1=0, A2x+B2y+C2=0 и A3x+B3y+С3=0 пересе-
каются в одной точке, то выполняется условие
|
A1 |
B1 |
C1 |
= 0. |
|
|
A2 |
B2 |
C2 |
(3.24) |
|
|
A3 |
B3 |
C3 |
Обратно, если имеет место (3.24), то три прямые A1x+B1y+С1=0, A2x+B2y+C2=0, A3x+B3y+С3=0 пересекаются в одной точке или параллельны.
Уравнение прямой, проходящей через точку M1(x1; y1) параллельно прямой Ах+Ву+С=0, может быть записано в виде
А(х–х1)+В(у–у1)=0. (3.25)
Пример 3.6. Определить острый угол между прямыми y= –3x+7; y=2x+1.
Ре ш е н ие . k1= –3; k2=2. По формуле (3.21) с учетом того, что угол между прямыми должен быть острым, имеем:
|
tgj = |
2 — (—3) |
=1Þ j = p/4. |
|||
|
1+ (—3)2 |
|||||
Пример 3.7. Исследовать расположение на плоскости двух прямых:
1)3x + 4y —1 = 0 и 2x + 3y —1 = 0;
2)2x + 3y +1 = 0 и 4x + 6y + 3 = 0;
3)x + y +1 = 0 и 3x + 3y + 3 = 0.
Ре ш е н ие : 1) прямые 3x + 4y —1 = 0 и 2x + 3y —1 = 0 пересекаются, так как 32 ¹ 43 . Координаты точки пересечения x = —1, y =1 найдены из решения системы двух линейных уравнений, задаюющих каждую прямую;
94

|
2) |
Прямые 2x + 3y +1 = 0 и 4x + 6y + 3 = 0 параллельны, так как |
||||
|
2 |
= |
3 |
¹ |
1 |
(система данных уравнений, очевидно, несовместна, так как умно- |
|
4 |
6 |
3 |
жая первое из них на 2 и отнимая от второго, получим противоречивое равенст-
во 1=0);
3) Прямые x + y +1 = 0 и 3x + 3y + 3 = 0 совпадают друг с другом, так как 13 = 13 = 13 (данные уравнения равносильны).
Пример 3.8. Даны вершины треугольника А(0; 1), B(6; 5), C(12; –1). Найти уравнения высоты и медианы, проведенных из вершины С.
|
Ре ш е н ие . |
Находим уравнение стороны АВ: |
x — 0 |
= |
y —1 |
; |
x |
= |
y —1 |
; |
||||||||||||
|
6 |
|||||||||||||||||||||
|
2 x +1. |
6 — 0 |
5 —1 |
4 |
||||||||||||||||||
|
4x=6y–6 или 2x–3y+3=0; y = |
|||||||||||||||||||||
|
3 |
|||||||||||||||||||||
|
Ищем уравнение высоты в виде: y — y1 = k(x — x1 ) или, с учетом того, что |
|||||||||||||||||||||
|
она опущена из вершины C(12; –1): y —12 = k(x +1). Коэффициент k |
опреде- |
||||||||||||||||||||
|
лим из условия (3.23) 2 k = —1 или k = — |
3 . Таким образом, искомое уравнение |
||||||||||||||||||||
|
3 |
2 |
||||||||||||||||||||
|
высоты имеет вид y —12 = —1,5(x +1) или y = —1,5x +10,5. |
|||||||||||||||||||||
|
Для записи уравнения медианы, найдем координаты середины стороны |
|||||||||||||||||||||
|
АВ по формулам (3.6): |
|||||||||||||||||||||
|
xM= |
x1 + x2 |
= 0 + 6 = 3, |
yM= |
y1 + y2 |
= 1+ 5 |
= 3. |
|||||||||||||||
|
2 |
2 |
2 |
2 |
||||||||||||||||||
|
Уравнение |
медианы |
CM запишем, |
используя |
уравнение |
(3.18): |
||||||||||||||||
|
x — 3 |
= |
y — 3 |
или —4(x — 3) = 9(y — 3). Окончательно имеем y = — |
4 x + 4 1 – |
|||||||||||||||||
|
12 — 3 |
|||||||||||||||||||||
|
—1— 3 |
9 |
3 |
искомое уравнение медианы.
Пример 3.9. Найти проекцию точки Р(4; 9) на прямую, проходящую че-
рез точки A(3; 1) и В(5; 2).
Ре ш е н ие . Искомая точка есть точка пересечения прямой АВ с перпендикуляром, опущенным на эту прямую из точки Р. Прежде всего, составим
уравнение прямой АВ. Применяя соотношение (3.18), получаем x 2— 3 = y1—1
или y = 12 x — 12 .
Чтобы составить уравнение перпендикуляра, опущенного из точки Р на прямую АВ, напишем уравнение произвольной прямой, проходящей через точку Р; согласно соотношению (3.14), получаем y — 9 = k(x — 4), где k — пока
еще не определенный угловой коэффициент. Нам нужно, чтобы искомая прямая
95

прошла перпендикулярно к АВ; следовательно, ее угловой коэффициент должен удовлетворять условию перпендикулярности с прямой АВ. Так как угловой ко-
эффициент прямой АВ равен 12 , то, согласно формуле (3.23), находим k = —2.
Подставляя найденное значение k в уравнение, получаем y — 9 = —2(x — 4) или y = —2x +17.
Решив систему уравнений y = 12 x — 12 и y = —2x +17 , найдем координа-
ты искомой проекции: x = 7, y = 3.
Пример 3.10. Составить уравнение прямой, проходящей через точку А(–2; –3) и начало координат.
|
Ре ш е н ие . Подставляя |
в (3.18) х1 = у1 = 0; x2 = –2; y2 = –3, имеем |
|||||||||
|
x — 0 |
= |
y — 0 |
или |
x |
= |
y |
. |
Преобразовывая последнее равенство, получаем |
||
|
—2 — 0 |
—3 — 0 |
—2 |
—3 |
|||||||
общее уравнение искомой прямой 3x — 2y = 0.
Пример 3.11. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Ре ш е н ие . Уравнение прямой имеет вид ax + by =1. По условию a=b>0
и ab/2=8. Значит, a=4. Таким образом, искомое уравнение прямой 4x + 4y =1 или в общем виде х+у–4=0.
Пример 3.12. Определить расстояние между двумя параллельными пря-
мыми 4x — 3y — 8 = 0 и 4x — 3y + 7 = 0.
|
Ре ш е н ие . |
Для решения задачи достаточно найти расстояние от любой |
|||||||
|
точки на одной |
из прямых до другой прямой. Возьмем |
точку на |
прямой |
|||||
|
4x — 3y — 8 = 0 . Пусть y = 0, тогда x = 2 . По формуле (3.11) |
найдем расстояние |
|||||||
|
от точки (2;0) до прямой 4x — 3y + 7 = 0. Получим d = |
4× 2 |
— 3×0 + 7 |
= |
15 = 3. |
||||
|
16 + 9 |
||||||||
|
5 |
Пример 3.13. Определить линейную зависимость y=kx+b между полными издержками y производства предприятия, изготавливающего однородную
продукцию, и объемом x производства, если:
1) постоянные издержки (например, затраты на содержание административных
зданий, их отопление и т.д.), не зависящие от объема продукции, составляют b (денежных единиц); 2) переменные издержки (например, материальные затраты) прямо пропорцио-
нальны с коэффициентом k объему х изготавливаемой продукции.
96

Записать эту зависимость для b = 4 (млн руб.) и k = 0,5 (млн руб. на одну единицу продукции).
Ре ш е н ие . В данном случае между полными издержками y некоторого производства и количеством x произведенной продукции имеет место линейная зависимость вида y=kx+b , где k – удельные переменные издержки (издержки на одну условную единицу продукции), а b – постоянные издержки производства. В случае b=4 (млн руб.) и k=0,5 (млн на одну условную единицу продукции) имеем уравнение y = 0,5x + 4.
Пример 3.14. Полные издержки y по производству х единиц продукции на двух предприятиях выражаются соответственно формулами:
L1 : y = 0,7x + 2 и L2 : y = 0,5x + 4,
где х – объем продукции (усл. ед.), а y – соответствующие полные издержки (млн руб.). Требуется выяснить, начиная с какого объема продукции более экономичным становится второе предприятие.
Ре ш е н ие . Построим прямые L1 и L2 (рис. 3.8)
Рис. 3.8
Найдем координаты точки их пересечения, решив следующую систему
|
уравнений: |
|||||||
|
ìy = 0,7x + 2, |
ì0,7x + 2 = 0,5x + 4, |
Û |
ì |
0,2x = 2, |
Û |
ìx =10, |
|
|
í |
Û í |
y = 0,5x + 4 |
í |
í |
|||
|
î y = 0,5x + 4 |
î |
îy = 0,5x + 4 |
î y = 9. |
Следовательно, точка А пересечения прямых имеет координаты х=10 и у=9. Это значит, что при объеме продукции х=10 усл.ед. полные издержки по производству этого объема на обоих предприятиях одинаковы и составляют 9 млн руб.
Из рис.3.8 видно, что при объеме х>10 более экономичным (издержки меньше) становится второе предприятие. Это можно установить и без помощи графика (аналитически).
97

Действительно, если обозначить y1 = 0,7x + 2 и y2 = 0,5x + 4, то, решая относительно х неравенство у2 < у1, получаем: 0,5х + 4 < 0,7x + 2 Û 0,2x > 2 Û x > 10.
Пример 3.15. Между пунктами А(5;5) и В(8;4) (на плане местности размеры даны в километрах) проложен прямолинейно провод телефонной связи. Необходимо подключить к этому проводу пункт С(2;1) по кратчайшему расстоянию. Найти точку подключения D и длину необходимого для этого провода.
Ре ш е н ие . Наикратчайшим расстоянием от пункта С(2;1) до прямой АВ является длина перпендикуляра СD, опущенного на АВ из точки С. Следовательно, необходимо найти уравнение прямой СD, перпендикулярной АВ и установить длину отрезка СD.
|
По формуле (3.18) запишем уравнение прямой АВ |
x |
— 5 |
= |
y |
— 5 |
. |
|
8 |
— 5 |
— 5 |
||||
|
4 |
Приводя подобные, получаем уравнение прямой в общем виде х+3у–20=0.
Так как угловой коэффициент прямой АВ kAB = — 13 , то угловой коэффициент
прямой CD kCD = 3. Тогда по формуле (3.14) уравнение прямой CD имеет вид
3(х–2)=(у–1) или в общем виде 3х–у–5=0.
|
Найдем координаты точки D. |
|||||||
|
ì |
3x — y — 5 = 0, |
Þ D(3,5; 5,5). |
|||||
|
D : í |
|||||||
|
îx + 3y — 20 = 0. |
|||||||
|
Обозначим |
через d расстояние от точки С до прямой АВ, тогда |
||||||
|
d = |
2 + 3×1— 20 |
= |
3 |
10 » 4,7 (км). |
|||
|
1+ 9 |
2 |
||||||
Следовательно, точка подключения к телефонному проводу будет иметь на плане местности координаты (3,5; 5,5), а длина требующегося провода составит 4,7 км.
Задачи для самостоятельного решения
3.52.Определить, какие из точек М1(3; 1), М2(2; 3), М3(6; 3), М4(–3; –3),
М5(3; –1), М6(–2; 1) лежат на прямой 2x–3у–3=0 и какие не лежат на ней.
3.53.Точки Р1, Р2, Р3, P4 и P5 расположены на прямой 3x–2у–6=0; их абсциссы соответственно равны числам 4, 0, 2, –2 и –6. Определить ординаты этих точек.
3.54.Точки Q1, Q2, Q3, Q4 и Q5 расположены на прямой х–3у+2=0; их ординаты соответственно равны числам 1, 0, 2, –1, 3. Определить абсциссы этих точек.
98
3.55.Определить точки пересечения прямой 2х–3у–12=0 с координатными осями и построить эту прямую на чертеже.
3.56.Найти точку пересечения двух прямых 3x–4y–29=0 и 2х+5у+19=0.
3.57.Стороны АВ, ВС и АС треугольника ABC даны соответственно уравнениями 4x+3у–5=0, х–3у+10=0, х–2=0. Определить координаты его вершин.
3.58.Даны уравнения двух сторон параллелограмма 8x+3y+1=0, 2x+y-1=0 и уравнение одной из его диагоналей 3x+2у+3=0. Определить координаты вершин этого параллелограмма.
3.59.Стороны треугольника лежат на прямых x+5у–7=0, 3x–2y–4=0, 7x+y+19=0. Вычислить его площадь S.
3.60.Площадь треугольника S=8 кв. ед.; две его вершины находятся в точках A(1; –2) и В(2; 3), а третья вершина С лежит на прямой 2х+у-2=0. Определить координаты вершины С.
3.61.Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Оу:
|
1) k = |
2 |
, b = 3; |
2) k = 3, b = 0; |
3) k = 0, b = –2; |
||||
|
3 |
3 |
1 |
2 . |
|||||
|
4) k =– |
, b = 3; |
5) k = –2, b = –5; |
6) k = – |
, b = |
||||
|
4 |
3 |
3 |
3.62.Определить угловой коэффициент k и отрезок b, отсекаемый на оси Оу, для каждой из прямых:
1) 5х–у+3=0; 2) 2х+3у–6=0; 3) 5х+3у+2=0; 4) 3x+2y=0; 5) y–3=0.
3.63.Дана прямая 5х+3у–3=0. Определить угловой коэффициент k прямой:
1)параллельной данной прямой;
2)перпендикулярной к данной прямой.
3.64.Дана прямая 2х+3у+4 = 0. Составить уравнение прямой, проходящей через точку M0(2; 1):
1)параллельно данной прямой; 2) перпендикулярно к данной прямой.
3.65.Даны уравнения двух сторон прямоугольника x–2у=0, х–2y+15=0 и уравнение одной из его диагоналей 7x+y–15=0. Найти вершины прямоугольника.
3.66.Найти проекцию точки Р(–6; 4) на прямую 4x–5у+3=0.
3.67.Найти точку Q, симметричную точке Р(–5; 13) относительно прямой
2х–3у–3=0.
3.68.В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и находящейся на равном расстоянии от каждой прямой:
|
1) |
5x+y+3=0 и 5x+y–17=0; |
2) |
2x+3y–6=0 и |
4х+6у+17=0; |
|
3) |
5х+7y+15=0 и 5х+7у+3=0; |
4) |
3х–15у–1=0 и |
х–5у–2=0. |
99
3.69.Вычислить угловой коэффициент k прямой, проходящей через две данные точки:
|
а) M1(2; –5), М2(3; 2); |
б) P(–3; 1), Q(7; 8); |
в) A(5; –3), В(–1; 6). |
3.70.Составить уравнения прямых, проходящих через вершины треугольника A (5; –4), В(–1; 3), С(–3; –2) параллельно противоположным сторонам.
3.71.Даны середины сторон треугольника: М1(2; 1), М2(5; 3) и М3(3; –4). Составить уравнения его сторон.
3.72.Даны две точки: Р(2; 3) и Q(–1; 0). Составить уравнение прямой, проходящей через точку Q перпендикулярно к отрезку PQ.
3.73.Составить уравнение прямой, если точка Р(2; 3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
3.74.Стороны треугольника даны уравнениями 4х–у–7=0, х+3у–31=0, х+5у–7=0. Определить точку пересечения его высот.
3.75.Даны вершины треугольника А(2; –2), В(3; –5) и С(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине A.
3.76. Составить уравнения сторон и медиан треугольника с вершинами
A(3; 2), В(5; –2), С(1; 0).
3.77.Даны две смежные вершины А(–3; –1) и B(2; 2) параллелограмма АВСD и точка Q(3; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.
3.78. Даны уравнения двух сторон прямоугольника 5х+1у–7=0, 5х+2у–36=0 и уравнение его диагонали 3х+7у–0=0. Составить уравнения остальных сторон и второй диагонали этого прямоугольника.
3.79.Составить уравнение прямой, проходящей через точку Р(3; 5) на одинаковых расстояниях от точек А(–7; 3) и B(11; –15).
3.80.Найти точку М1, симметричную точке M2(8; –9) относительно прямой, проходящей через точки A(3; –4) и B(–1; –2).
3.81.На прямой 2х–у–5=0 найти такую точку Р, сумма расстояний которой до точек А(–7; 1), B(–5; 5) была бы наименьшей.
3.82.На прямой 3x–у–1=0 найти такую точку Р, разность расстояний которой до точек A(4; 1) и B(0; 4) была бы наибольшей.
3.83.Дана прямая 2x+3у+4=0. Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 45° к данной прямой.
3.84.Точка А(–4; 5) является вершиной квадрата, диагональ которого лежит на прямой 7x–у+8=0. Составить уравнения сторон и второй диагонали этого квадрата.
100
3.85.Даны две противоположные вершины квадрата А(–1; 3) и С(6; 2). Составить уравнения его сторон.
3.86.Точка E(1; –1) является центром квадрата, одна из сторон которого лежит на прямой x–2у+12=0. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
3.87.Составить уравнение прямой, проходящей через точку M1(2; –3) параллельно прямой:
|
1) 16х–24у–7=0; |
2) 2х+3=0; |
3) 3у–1=0. |
3.88. Установить, какие из следующих пар прямых перпендикулярны:
|
1) |
3х–4у+1=0 и 4х–3у+7=0; |
2) |
6х–15у+7=0 и 10х+4у–3=0; |
|
3) |
9х–12у+5=0 и 8х+6y–13=0; |
4) |
7х–2у+1=0 и 4х+6у+17=0. |
3.89.Даны две вершины А(3; –1) и В(5; 7) треугольника ABC и точка N(4; –1) пересечения его высот. Составить уравнения сторон этого треугольника.
3.90.В треугольнике ABC даны: уравнение стороны АВ: 5х–3у+2=0, уравнения высот AN: 4x–3у+1=0 и BN: 7x+2y–22=0. Составить уравнения двух других сторон и третьей высоты этого треугольника.
3.91.Составить уравнения сторон треугольника ABC, если даны одна из его вершин A(1; 3) и уравнения двух медиан х–2у+1=0 и у–1=0.
|
3.92. Составить |
уравнения |
сторон |
треугольника, |
зная |
одну |
его |
вершину |
|||
|
В(2; |
–1), |
а |
также |
уравнения |
высоты 3x–4y+27=0 и |
биссектрисы |
||||
|
х+2у–5=0, проведенных из различных вершин. |
||||||||||
|
3.93. Составить |
уравнения |
сторон |
треугольника, |
зная |
одну |
его |
вершину |
|||
|
А(3; |
–1), |
а |
также |
уравнения |
биссектрисы x–4у+10=0 |
и |
медианы |
6x+10y–59=0, проведенных из различных вершин.
3.94.Составить уравнение прямой, которая проходит через начало координат и вместе с прямыми х–у+12=0, 2х+у+9=0 образует треугольник с площадью, равной 1,5 кв.ед.
3.95.Среди прямых, проходящих через точку P(3; 0), найти такую, отрезок которой, заключенный между прямыми 2x–у–2=0, х+y+3=0, делится в точке P пополам.
3.96.Составить уравнение прямой, проходящей через точку С(–5; 4), зная, что длина ее отрезка, заключенного между прямыми x+2y+1=0, x+2y–1=0, равна 5.
3.97.Определить, при каком значении а прямая (а+2)x+(а2–9)y+3а2–8а+5=0
|
1) |
параллельна оси абсцисс; |
2) параллельна оси ординат; |
|
3) |
проходит через начало координат. |
В каждом случае написать уравнение прямой.
3.98.Определить, при каких значениях т и п прямая
101
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Прямая:
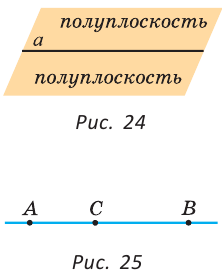
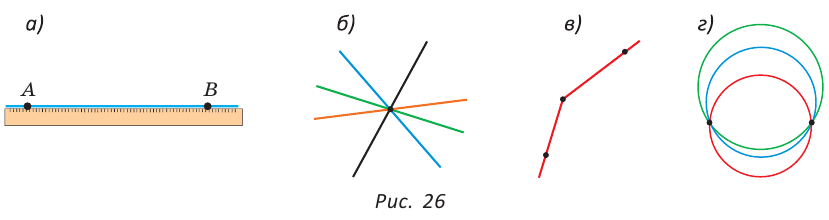
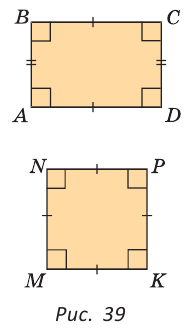
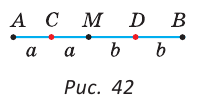
Прямая бесконечна (в обе стороны) и разбивает плоскость на две полуплоскости (рис. 24), для которых прямая является границей. Граница принадлежит полуплоскостям. На рисунке 25 точка С лежит на прямой между точками А и В, которые лежат по разные стороны от точки С. Точки С и В лежат по одну сторону от точки А. Из трех точек на прямой одна и только одна точка лежит между двумя другими.
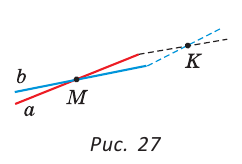
Если на плоскости отметить две точки А и В, то через них всегда можно провести прямую АВ (рис. 26, а). Через одну точку можно провести бесконечно много прямых (рис. 26, б), через три точки не всегда можно провести прямую (рис. 26, в). Через две точки можно провести бесконечно много окружностей (рис. 26, г), а прямую — только одну!
Аксиома прямой. Через любые две точки плоскости можно провести прямую, и притом только одну.
Из аксиомы следует, что если две прямые (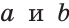
Определение. Две прямые называются пересекающимися, если они имеют общую точку.
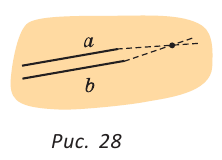
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Если прямые 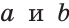
Луч:
Определение. Лучом называется часть прямой, ограниченная одной точкой.
Точка, ограничивающая луч, принадлежит лучу и называется началом луча. Луч бесконечен (в одну сторону). Он обозначается одной малой буквой, или двумя большими буквами, где первой всегда записывается начало луча.
При этом вторая точка может быть не отмечена на луче. Она указывает направление луча, например как точка В на луче АВ (рис. 29).
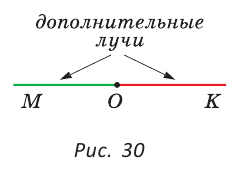
Определение. Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой.
На рисунке 30 изображены дополнительные дополнительные лучи ОМ и ОК. Они дополняют друг друга до прямой. Чтобы построить луч, дополнительный данному, достаточно продлить данный луч за его начало вдоль прямой, на которой лежит данный луч. Любая точка прямой разбивает ее на два дополнительных луча.
Отрезок:
Определение. Отрезком называется часть прямой, ограниченная двумя точками.
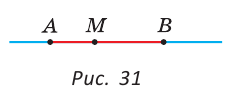
Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. На рисунке 31 изображен отрезок АВ с концами А и В. Точка М — внутренняя точка отрезка АВ.
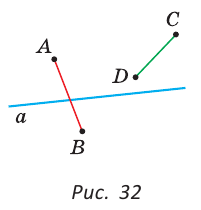
Если концы отрезка лежат в разных полуплоскостях относительно прямой, то этот отрезок пересекает прямую, если в одной полуплоскости — то не пересекает. На рисунке 32 концы отрезка АВ лежат в разных полуплоскостях относительно прямой а, и он пересекает прямую 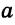
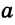
Если при наложении отрезков их концы совпадут, то по аксиоме прямой эти отрезки совпадут всеми своими точками.
Определение. Два отрезка называются равными, если их можно совместить наложением.
Важной характеристикой отрезка является его длина.
Свойства длины отрезка: каждый отрезок имеет длину, выраженную положительным числом; равным отрезкам соответствуют равные длины, большему отрезку — большая длина. И наоборот.
Аксиома измерения отрезков. Если на отрезке взять точку, то она разобьет данный отрезок на два отрезка, сумма длин которых равна длине данного отрезка.
Аксиома откладывания отрезков. На любом луче от его вершины можно отложить отрезок данной длины, и притом только один.
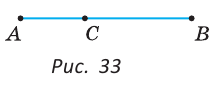
На рисунке 33 точка С лежит на отрезке АВ. По аксиоме измерения отрезков следует, что АС + СВ=АВ.
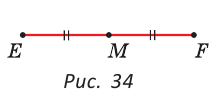
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке 34 точка М — середина отрезка EF, то есть ЕМ = MF.
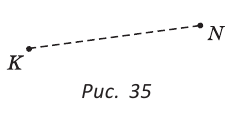
Определение. Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
На рисунке 35 расстояние между точками К и N равно длине отрезка KN.
Ломаная:
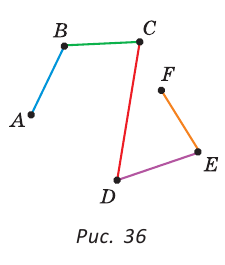
На рисунке 36 отрезки АВ, ВС, CD, DE и EF последовательно соединены своими концами: отрезок ВС соединен с отрезком АВ, отрезок CD соединен с отрезком ВС и так далее. Полученная фигура представляет собой ломаную ABCDEF. Указанные отрезки называются звеньями ломаной, а точки А, В, С, D, Е и F — вершинами ломаной.
Определение. Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами, у которой никакие два соседних звена не лежат на одной прямой. Длиной ломаной называется сумма длин ее звеньев.
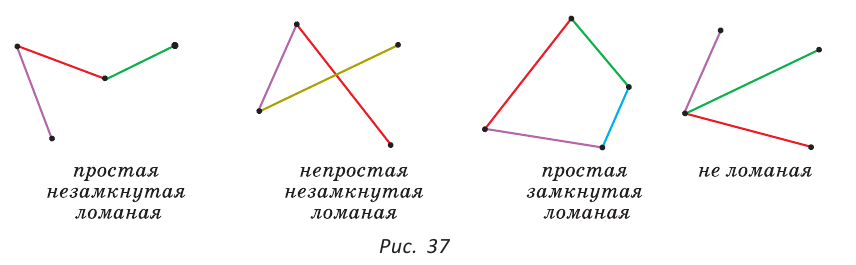
Определение. Ломаная называется замкнутой, если начало ее первого звена совпадает с концом последнего. В противном случае она называется незамкнутой. Ломаная называется простой, если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек. В противном случае она называется непростой (рис. 37).
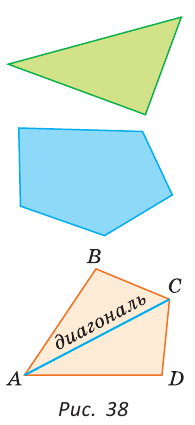
Простая замкнутая ломаная на плоскости называется многоугольником. Звенья этой ломаной называются сторонами этого многоугольника, а вершины — вершинами многоугольника. Периметром многоугольника называется сумма длин его сторон. Часть плоскости, ограниченная многоугольником, называется плоским многоугольником. Слово «плоский» употреблять не будем. Отрезок, соединяющий вершины многоугольника, не принадлежащие одной стороне, называется его диагональю. Если у многоугольника три стороны, то у него три вершины и три угла, и он называется треугольником, если четыре стороны — четырехугольником, если пять — пятиугольником и так далее.
На рисунке 38 изображен четырехугольник ABCD со сторонами АВ, ВС, CD и AD. У него четыре угла: 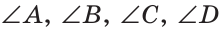
При записи многоугольника его вершины записываются последовательно, начиная с любой вершины и в любом направлении. Например, СBAD — это тот же четырехугольник ABCD.
Самые известные четырехугольники — это прямоугольник и квадрат. У прямоугольника все углы прямые, а противоположные стороны равны. Квадрат — это прямоугольник, у которого все стороны равны. На рисунке 39 ABCD — прямоугольник, MNPK — квадрат. Позже мы дадим определение прямоугольника и квадрата и рассмотрим их свойства подробно. А пока будем пользоваться указанными представлениями.
Пример:
На отрезке АВ, равном 24 см, взята точка С. Отрезок АС на 6 см больше отрезка СВ. Найти длину отрезка АС.
Решение:
Пусть СВ = 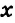
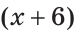
По аксиоме измерения отрезков 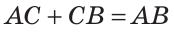
То есть, 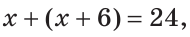
Ответ: 15 см.
Замечание. В дальнейшем при решении задач не будем ссылаться на аксиому измерения отрезков.
Пример:
На отрезке АВ отмечены точки С и D (рис. 41). Найти длину отрезка CD, если:
Решение:
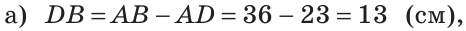
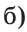
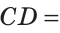
Ответ: а) 6 см; б)
Пример:
На отрезке АВ, равном 42 см, взята точка М. Найти расстояние между серединами отрезков AM и MB.
Решение:
Пусть С — середина отрезка AM, D — середина отрезка MB.
Обозначим 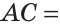
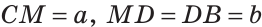
Тогда 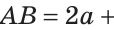
Следовательно, 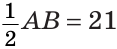
Ответ: 21 см.
Замечание. В данной задаче мы доказали свойство: «Если на отрезке отмечена точка, то расстояние между серединами полученных отрезков равно половине данного отрезка». Утверждения, которые будут доказаны нами в ключевых задачах, могут в дальнейшем использоваться как известные свойства.
Прямая в высшей математике
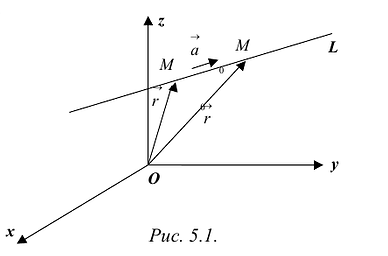
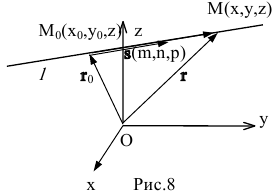
Прямая L в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой). Пусть задана такая точка 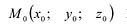
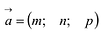
Если М(х, у, z) — произвольная текущая точка прямой L, то вектор 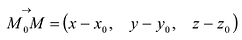
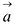
Этим соотношениям удовлетворяют координаты любой точки прямой L и только этой прямой. Равенства (5.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 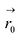
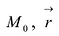
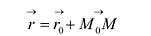
В силу коллинеарности векторов 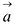
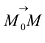
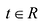
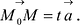
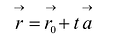
В координатной форме уравнение (5.3) равносильно трем уравнениям:
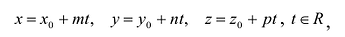
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (5.4) параметр t, легко перейти к каноническим уравнениям прямой (5.1).
Обратный переход от (5.1) к (5.4) осуществляют, приравнивая каждое из трех соотношений (5.1) к t. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 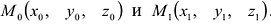
Очевидно, что в этом случае направляющим вектором прямой L будет вектор 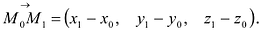
Прямую L в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии L в общем виде:
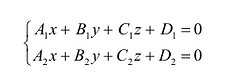
Система двух уравнений первой степени (5.6) определяет прямую линию при условии, что нормальные векторы 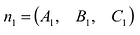
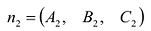
Чтобы перейти от общих уравнений прямой (5.6) к ее каноническим уравнениям (5.1), нужно на прямой найти какую-нибудь точку 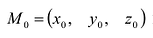
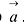
Точку 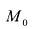
Направляющий вектор 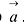
Поэтому в качестве 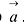
- Заказать решение задач по высшей математике
Понятие прямой
Нормальным вектором прямой называется любой вектор, перпендикулярный прямой.
Направляющим вектором прямой называется любой вектор, лежащий на этой прямой.
Взаимное расположение прямых
Пусть даны две прямые:
Эти прямые заданы своими точками 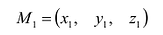
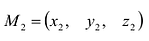
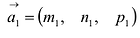
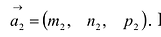
Параллельность или перпендикулярность прямых равносильна, соответственно, параллельности или перпендикулярности их направляющих векторов. Поэтому условие перпендикулярности прямых можно записать в виде:
Условие параллельности:
Возможны четыре случая взаимного расположения прямых:
Условие (5.8) выполняется в случаях I-III и означает, что прямые лежат в одной плоскости.
Уравнения прямой на плоскости
1. Па плоскости Оху составим уравнение прямой l, проходящей через точку 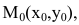
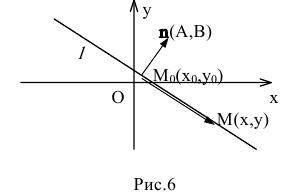
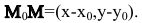
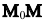
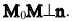
В координатной форме это равенство примет вид:
Уравнение Ах+Ву+С=0, где А и В не равны одновременно нулю 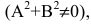
Если 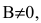
притом 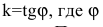
Вывод. Прямая на плоскости однозначно определяется точкой и нормальным вектором.
2. Па плоскости Оху составим уравнение прямой l, проходящей через точку 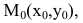
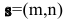
Пусть М(х,у) — произвольная точка прямой l, 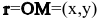
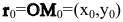
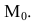
Так как векторы 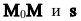
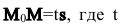
или в координатной форме параметрические уравнения прямой:
Пусть m и n отличны от нуля. Разрешим каждое из уравнений относительно t:
откуда получаем каноническое уравнение прямой:
Пусть прямая l проходит через две точки 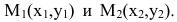
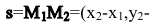
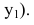
Вывод. Прямая однозначно определяется точкой и направляющим вектором.
Пример:
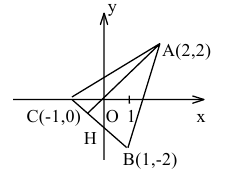
Вершины треугольника находятся в точках А(2,2), В(1,-2), С(-1,0). Найти проекцию точки А на основание ВС.
Решение:
Построим чертеж.
Проекция точки А на ВС есть точка пересечения основания ВС с перпендикуляром, опущенным из А на ВС.
Составим уравнение прямой ВС по двум точкам:
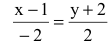
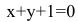
Обозначим искомую проекцию точкой Н(х,у). Т.к. 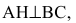
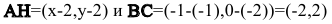
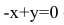
Теперь найдем проекцию точки А на основание ВС. Для этого решим систему: 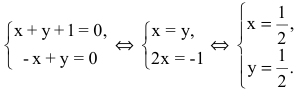
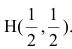
Замечание. Уравнение прямой АН можно было находить другими способами. Например, из общего уравнения прямой ВС х+у+1=0 можно выписать координаты нормального вектора 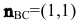
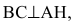
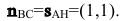
По нормальному вектору 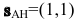
Уравнения прямой в пространстве
Уравнения прямой l, проходящей через точку 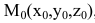
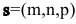
Пусть M(x,y,z) — произвольная точка прямой 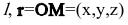
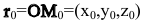
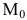
Тогда векторное уравнение прямой останется прежним: 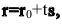
Параметрические уравнения прямой примут вид:
В случае 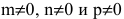
Наконец, составим уравнения прямой, проходящей через две точки
Внимание! В пространстве точка и нормальный вектор однозначным образом определяют плоскость. Поэтому в пространстве общие уравнения прямой будут задаваться линией пересечения двух плоскостей.
- Плоскость — определение, виды и правила
- Кривые второго порядка
- Евклидово пространство
- Матрица — виды, операции и действия с примерами
- Корень из числа — нахождение и вычисление
- Теория множеств — виды, операции и примеры
- Числовые множества
- Вектор — определение и основные понятия
Государственное образовательное учреждение
Среднего профессионального образования
«Котовский индустриальный техникум»
МАТЕМАТИКА
Модуль по теме:
«Прямая на плоскости и ее уравнения»
Котовск, 2014
г.
Учебное пособие для студентов техникума II курса
Авторы:
Т.А. Букатина – преподаватель математики.
Модуль содержит теоретический материал, необходимый при
изучении темы: «Прямая на плоскости и ее уравнения». В конце изложения теории
приводятся примеры решения типовых задач по данной теме. Модуль завершается
блоком заданий для самостоятельной работы, вопросами для повторения и зачетными
заданиями.
Модуль составлен в соответствии с программой по
математике, рекомендованной Министерством образования и науки РФ для средних
специальных учебных заведений.
Данный модуль может быть использован на учебных занятиях
и для самостоятельной подготовки студентов всех специальностей.
Прямая на плоскости и её уравнения
1.
Уравнение линии
на плоскости
Рассмотрим уравнение
, (1)
где и
—
произвольные переменные, принимающие действительные значения.
Известно, что решением уравнения
(1) является любая упорядоченная пара значений переменных и
,
обращающая это уравнение в верное равенство. Заметим, что уравнению (1) может
удовлетворять одна пара действительных чисел, несколько и даже бесконечное
множество таких пар. Например, уравнению удовлетворяет
единственная пара чисел и
. Уравнению
удовлетворяет
любая пара чисел и
, где
— произвольное число. Существуют уравнения
вида (1), которым не удовлетворяет ни одна пара действительных чисел. Такими,
например, являются уравнения ,
.
Зададим на плоскости систему
координат . Если рассматривать множество пар
значений переменных и
,
удовлетворяющих уравнению (1), как координаты точек на плоскости, то
множество этих точек представляет график уравнения (1), который, вообще
говоря, есть некоторая линия .
Таким образом, уравнению с
переменными и
соответствует
на плоскости, вообще говоря, некоторая линия, координаты точек которой
удовлетворяют данному уравнению. Построение графиков функций можно
рассматривать как примеры нахождения линий, соответствующих данным уравнениям.
Не менее важной является
обратная задача: по данной на плоскости линии найти соответствующее ей
уравнение.
Пример №1:
Лежат ли точки и
на линии
?
Подставив в данное
уравнение вместо и
координаты
точки , получим
.
Следовательно, точка лежит
на данной линии. Подставим координаты точки :
,
т.е. точка не
лежит на данной линии.
ч.т.д.
2. Уравнение прямой, проходящей через
данную точку перпендикулярно данному вектору
Пусть в плоскости заданы некоторая точка
и ненулевой вектор
с координатами
.
Требуется составить уравнение прямой , проходящей через точку
и перпендикулярной вектору
(рис. 1).

(рис. 1)
Определение. Любой ненулевой вектор ,
перпендикулярный прямой , называется нормальным
вектором этой прямой. ;
.
Очевидно, что через точку в плоскости
проходит
единственная прямая , имеющая нормальный вектор
. Возьмем на прямой
произвольную точку
.
Тогда вектор перпендикулярен вектору
и, следовательно, их скалярное
произведение равно нулю, т.е.
.
(1)
Учитывая, что и
, выразим равенство (1) в координатной
форме:
. (2)
—
уравнение прямой, проходящей через данную точку, с данным
нормальным
вектором
где —
координаты нормального вектора
—
текущие координаты
—
координаты точки, через которую проходит прямая
Пример №1:
Составить уравнение прямой, проходящей через
точку перпендикулярно вектору
.
Из условия задачи
имеем
,
,
,
.
Подставив эти значения в уравнение (2),
получим
.
ч.т.д.
Упражнения:
1. Составить уравнение прямой, проходящей
через начало координат перпендикулярно вектору .
2. Составить уравнение прямой, проходящей
через точку перпендикулярно вектору
.
3. Составить уравнение прямой, проходящей
через середину отрезка перпендикулярно
к нему, если и
.
3. Общее
уравнение прямой и неполные уравнения прямой
3.1 Общее
уравнение прямой
Пусть дана произвольная прямая.
Выберем на ней некоторую точку , и пусть
— произвольный нормальный вектор этой
прямой, тогда (из п.2) уравнением этой прямой будет уравнение . Запишем его так:
,
; обозначив число-
С,
получим .
—
общее уравнение прямой,
где
— текущие координаты,
— координаты нормального вектора.
Задача
Указать нормальные векторы для
прямых, заданных уравнениями 1);
2);
3)
Нормальным вектором первой
прямой является вектор ; второй- вектор
; третий — вектор
.
3.2 Неполные уравнения прямой
В общем уравнении прямой ,
могут
принимать различные действительные значения, исключая одновременное равенство
нулю и
.
Рассмотрим некоторые частные
случаи уравнения , получающиеся при равенстве
нулю отдельных его коэффициентов.
1)
Пусть в уравнении ,
=0,
тогда . Обозначим
,
получим .
— уравнение прямой
параллельной оси (рис. 2)
Если кроме того, , то
уравнение примет вид
.
— уравнение
прямой, совпадающей с осью .

рис. 2
2)
Пусть , тогда уравнение
примет
вид , или
,
положим
, получим
.
— уравнение
прямой параллельной оси (рис.3)

рис.3
Если же кроме того, , то уравнение
примет
вид .
—
уравнение прямой совпадающей с осью ординат (рис.4)

рис.4

Пусть в уравнении
, тогда
;
, положим
—
формула углового коэффициента прямой из общего уравнения прямой, получим
—
уравнение прямой, проходящей через начало координат (рис.5)

Определение: Условным коэффициентом прямой
называется тангенс угла наклона прямой к положительному направлению оси .
— определение
углового коэффициента прямой.
Пример:
Найти угловой коэффициент прямой .
,
.
Ответ: .
3.3 Уравнение
прямой с угловым коэффициентом и начальной ординатой
Рассмотрим общее уравнение
прямой
;
;
, получим
.
— уравнение прямой с угловым
коэффициентом и начальной ординатой
.
Пример №1.
Общее уравнение прямой записать
в виде .
Решение: I способ:
,
,
.
II способ:
.
Пример №2.
Составить уравнение прямой, образующей с положительным
направлением оси угол
и
отсекающей на оси отрезок, равный 4.
Дано:
.
Составить уравнение прямой .
Решение:
.
Ответ: .
Упражнения:
1.
Составить уравнение
прямой, проходящей через начало координат и составляющей с положительным
направлением оси углы: 1)
, 2)
.
2.
Найти угловой коэффициент
и начальную ординату прямой .
3.
Составить уравнение
прямой, проходящей через точку и имеющей начальную
ординату .
4.
Написать общее уравнение
прямой из данных прямых и найти координаты её нормального вектора: 1) , 2)
.
4.Другие формы уравнения прямой на
плоскости
В этом параграфе мы познакомимся
с некоторыми другими формами уравнения прямой на плоскости.
1. Уравнение прямой,
проходящей через данную точку с данным угловым коэффициентом. Пусть даны точка и
угловой коэффициент прямой, проходящей через точку
. Требуется составить уравнение искомой
прямой в виде
. (1)
В этом уравнении координаты и
нормального
вектора нам известны, поэтому постараемся их
исключить. Для этого разделим уравнение (1) на (
, в противном случае
не существует):
,
откуда
,
или
. (2)
Определение. Уравнение (2)
называется уравнением прямой, проходящей через данную точку с
данным угловым коэффициентом.
2. Уравнение прямой, проходящей через две
данные точки.
Пусть даны две различные точки и
.
Требуется составить уравнение прямой, проходящей через эти точки. Возьмем
произвольную точку на этой прямой (рис. 6).

рис. 6
Рассмотрим векторы и
.
(3)
Точки ,
и
лежат
на одной прямой тогда и только тогда, когда векторы (3) коллинеарны и,
следовательно, их координаты пропорциональны. При и
имеем
. (4)
Определение. Уравнение (4) называется уравнением прямой,
проходящей через две данные точки.
Если , то прямая параллельна оси
и, следовательно, её уравнение имеет вид
. (5)
Если , то
прямая параллельна оси и её уравнение имеет вид
. (6)
Пример:
Даны координаты точек и
. Составить уравнение прямой
.
Решение: ;
.
3. Уравнение прямой в отрезках.
Пусть требуется составить
уравнение прямой , отсекающей на оси
отрезок величиной
, а на оси
—
отрезок величиной
(рис.
7).

рис.
7
Обозначим точки пересечения
прямой с осями координат
и
соответственно
через точки и
. Тогда точка
имеет координаты
, а точка
—
координаты . Составим уравнение прямой
как прямой, проходящей через две
точки и
.
Заменив в (4) ,
координатами
точки и
,
— координатами точки
, получим
,
откуда
. (7)
Определение. Уравнение (7) называется уравнением в отрезках (оно
связывает текущие координаты и
и величины отрезков
и
,
отсекаемые прямой на осях координат).
Пример:
Построить прямую .
Решение: Преобразуем данное уравнение к виду (7); для этого
перенесем свободный член вправо и разделим обе части на него:
.
Сравнивая полученное уравнение с уравнением
(7), найдем и
.
Отложим на оси отрезок
величиной
и на оси
—
отрезок величиной
.
Прямая, проведенная через точки и
, будет искомой (рис.


рис. 8
Упражнения:
1.
Составить уравнение
прямой, проходящей через точку и образующей с
положительным направлением оси угол
.
2.
Составить уравнение
прямой, проходящей через точку и имеющей угловой
коэффициент, равный .
3.
Прямая проходит через
точки и
. Найти
отрезки, отсекаемые этой прямой на осях и
.
4.
Составить уравнение
прямой, проходящей через точку и отсекающей на оси
отрезок, равный
.
5.
Составить уравнение прямой
в отрезках, если она пересекает оси координат в точках:
1) и
2) и
.
6. Найти длину отрезка, заключенного между
точками пересечения прямой с осями координат.
7. Составить уравнение прямой, проходящей
через две заданные точки, если:
1) ;
2) ;
3) ;
4) .
8. Написать уравнения в отрезках и построить
следующие прямые:
1) ;
2) .
9. Найти площадь треугольника, ограниченного
прямой и осями координат.
5. Вычисление угла между прямыми
Пусть требуется определить угол
между прямыми и
,
заданными в плоскости уравнениями
,
.
Вычисление одного из смежных
углов между прямыми и
сводится
к вычислению угла между нормальными векторами
и
этих
прямых (рис. 9)

рис.
9
Но .
Записав правую часть последнего равенства в координатной форме, получаем 


формула вычисления угла между прямыми
Пример №1:
Найти угол между прямыми и
.
Решение: По формуле 
,
.
Если прямые и
заданы
соответственно уравнениями
и
,
то угол , на
который нужно повернуть прямую в положительном
направлении до совпадения с прямой , можно вычислить через
угловые коэффициенты и
этих
прямых. Из рис. 9 видно, что , откуда
.
Если прямые и
не
перпендикулярны, т.е. имеет смысл , то
.
Но ,
, поэтому
.
Пример №2:
Найти острый угол между прямыми и
.
Решение: Из уравнения находим
. Сравнивая уравнение
с уравнением
,
находим . По формуле имеем

В таблице тангенсов или при помощи
микрокалькулятора находим .
Упражнения:
1. Вычислить угол между прямыми:
1) и
;
2) и
;
3) и
;
4) и
.
2. Вычислить угол между прямой и прямой, проходящей через точки
и
.
3. Даны уравнения сторон треугольника :
,
,
. Найти внутренние углы треугольника.
6. Пересечение прямых.
Условие параллельности и перпендикулярности прямых
1.
Пересечение прямых
Пусть даны две прямые,
определяемые уравнениями
и
.
Требуется найти точку их пересечения. Точка
пересечения данных прямых есть их общая точка. Координаты этой точки удовлетворяют
как первому, так и второму уравнению, т.е. эти координаты являются общими
корнями данных уравнений.
Чтобы найти эти корни, нужно как
известно из алгебры, решить совместно данные уравнения, рассматривая их как
систему уравнений 
Пример:
Найти точку пересечения прямых и
.
Решение: Решим данные уравнения как систему
получим
, зная
, находим
,
например значение подставляем во второе
уравнение
Ответ: .
2.
Условие
параллельности прямых
Пусть даны на плоскости в
прямоугольной системе координат прямые
и
, и
заданные уравнениями и
(рис.
10)

рис. 10
,
(;
;
)
векторы
и
коллинеарны
значит их одноименные координаты пропорциональны, т.е. .

— условие параллельности
прямых

— условие совпадения
прямых
Перепишем равенство или
, т.к.
и
, то
.
— условие
параллельности прямых
Таким образом прямые параллельны
тогда и только тогда, когда их угловые коэффициенты равны между собой.
Пример №1:
Показать, что прямые и
параллельны
, если
.
Решение: —
(
;
)
—
(
;
)
.
Пример №2:
При каком значении прямые
и
будут
параллельны.
Решение:
Ответ: .
Пример №3:
Написать уравнение прямой, проходящей через
точку и параллельной прямой
.
Дано:
—
Написать уравнение
Решение:
;
Т.к. , то
—
(
;
)
;
Ответ: .
3.
Условие
перпендикулярности прямых
Пусть на плоскости в системе
координат даны два взаимно перпендикулярные прямые и
, заданные уравнениями
и
(рис.
11).

рис. 11
(;
;
;
;
)
.
—
условие перпендикулярности прямых

равенство , если
и
, то разделим обе части равенства на
, получим
или

и
, то
,
отсюда при имеем
.
—
условие перпендикулярности прямых
Таким образом, прямые
перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратные по
величине и противоположны по знаку.
Пример №1:
Показать, что прямые и
перпендикулярны.
Решение:
, если
—
(
;
)
—
(
;
)
.
Пример №2:
Написать уравнение прямой, проходящей через
точку и перпендикулярной прямой
.
Дано:
—
Написать уравнение
Решение:
—
(
;
)
;

;
Ответ: .
Упражнения:
1.
Найти точку пересечения
двух прямых:
1) и
;
2) и
.
2. Параллельны ли прямые:
1) и
;
2) и
;
3) и
.
3. Перпендикулярны ли прямые:
1) и
;
2) и
.
4. При каких значениях прямые
и
параллельны.
5. При каких значениях прямые
и
перпендикулярны.
6. Написать уравнение прямой, проходящей
через точку , параллельной прямой
.
7. Написать уравнение прямой, проходящей
через точку и перпендикулярной прямой
.
Вопросы для повторения:
1.
Какое вы знаете уравнение
линии на плоскости?
2.
Дайте определение
нормального вектора прямой.
3.
Каково уравнение прямой,
проходящей через данную точку и нормальным вектором?
4.
Какое уравнение прямой
называется общим?
5.
Какие вы знаете частные
случаи уравнения прямой?
6.
Каково уравнение прямой с
угловым коэффициентом и начальной ординатой?
7.
Какое знаете уравнение
прямой, проходящей через точку с заданным направлением (пучок прямых)?
8.
По какой формуле можно
написать уравнение прямой, проходящей через две точки?
9.
Что представляет собой
уравнение прямой в отрезках?
10.
Как найти угол между
прямыми.
11.
Какие условия параллельности
прямых знаете?
12.
Какие условия
перпендикулярности прямых знаете?
13.
По какой формуле можно
найти координаты точки пересечения прямых?
Зачетная работа
«Прямая на плоскости»
1.
Написать уравнение прямой,
проходящей через точку и перпендикулярной вектору
, если
и
.
2.
При каких значениях прямые
и
параллельны?
3.
При каких значениях прямые
и
перпендикулярны?
4.
Найти угол между прямыми и
.
5.
Определить длину отрезка
прямой , заключенного между точками пересечения
прямой с осями координат.
Литература:
1.
А.А. Дадаян «Математика»
Профессиональное образование
2.
Зайцев «Элементы высшей
математики»
3.
Г.Н. Яковлев «Математика
для техникумов»
4.
И.И. Валуцэ «Математика
для техникумов»
5.
Н.В. Богомолов
«Практические занятия по математике».