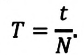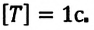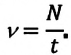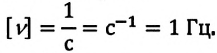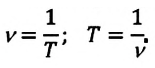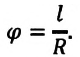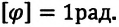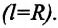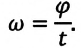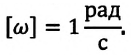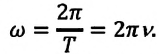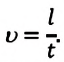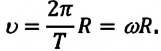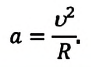Как найти длину пути по окружности

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Длина пройденного пути по окружности

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Движение по окружности

Наряду с движением вдоль прямой в школьной физике рассматривают движение по окружности. Для него, по аналогии с прямолинейным движением, вводятся понятия пройденного пути, скорости движения и ускорения.

В физике выделяют несколько видов движения тел. Движение по окружности – это один из случаев движения вдоль кривой линии — криволинейного движения.

Сравним понятия пройденного пути, скорости и ускорения для прямолинейного движения и движения по окружности.

Угловой путь

Для начала, вспомним, что линейное перемещение – это разница между конечным и начальным положением точки на оси (рис. 1).

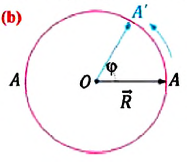
Рассмотрим теперь колесо (рис. 2). На горизонтальной линии, проходящей через диаметр колеса, справа отметим красную точку, от которой мы начнем отсчитывать углы. Условимся считать, что возле этой точки находится нулевой угол.

На ободе колеса выберем точку, например — ниппель. Сначала ниппель находился в точке 1. Точка 1 сдвинута на угол (gamma_ ) относительно начала отсчета.

Будем вращать колесо в направлении, обозначенном синей стрелкой. Повернем колесо на некоторый угол, так, чтобы к концу движения ниппель переместился в точку, обозначенную цифрой 2 на рисунке. Эта точка смещена на угол (gamma_ ) по отношению к началу отсчета.

По аналогии с поступательным движением, угловой путь, который прошел ниппель — это разница (разность) угловых положений точек 1 и 2.

(varphi left( text right)) – угловой путь измеряется в радианах.

Угловой путь – это угол, на который повернулся ниппель, по отношению к его начальному положению.

Угловая скорость — куда она направлена

Если тело двигалось равномерно (с неизменной скоростью), то линейную скорость можно определить по формуле

(v left( frac > right)) — линейная скорость – это путь, деленный на время, поэтому она имеет размерность метров деленных на секунду.

Аналогично линейному случаю, если угловой путь поделить на время движения, получим угловую скорость.

(omega left( frac > right)) – угловая скорость – это угловой путь, деленный на время, поэтому она имеет размерность радиан деленных на секунду.

Угловая скорость ( omega ), так же, как и линейная скорость, является вектором. Но в отличии от линейной скорости его направление можно определить по правилу буравчика (правого винта).

Примечание: Направление вектора угловой скорости ( vec ) можно определить по правилу буравчика (правого винта)!

На рисунке 3 окружность располагается в горизонтальной плоскости, а вектор ( vec ) направлен вдоль вертикальной оси вращения. Направление вращения указано синей стрелкой.

При движении по окружности вектор линейной скорости (vec ) изменяет свое направление. Но в каждой точке окружности вектор (vec ) направлен по касательной к окружности, т. е. перпендикулярно радиусу.

Примечание: Касательная и радиус перпендикулярны, это известно из геометрии.

Если точка начнет вращаться в противоположную сторону, то векторы линейной и угловой скорости развернутся противоположно направлениям, указанным на рисунке 3.

Связь между линейной и угловой скоростью

Угловая и линейная скорость связаны математически. Линейная скорость – это векторное произведение вектора угловой скорости и вектора радиуса окружности.

Примечание: Радиус окружности – это вектор, он направлен от центра окружности к ее внешней границе.

Скалярный вид записи связи скоростей:

(omega left( frac > right)) – угловая скорость;

(v left( frac > right)) — линейная скорость;

(R left( text right)) – радиус окружности.

Частота и период

Вращательное движение описывают с помощью таких характеристик, как частота и период.

Период обращения – это время одного полного оборота. В системе СИ период измеряют в секундах.

( T left(c right)) – время, за которое тело совершило полный оборот – период. Время – это скалярная величина.

Частота отвечает на вопрос: «Сколько полных оборотов совершило тело за одну секунду?».

( displaystyle nuleft( frac right)) – частота оборотов, скаляр.

Вместо записи ( displaystyle left( frac right)) иногда используют (displaystyle left( c^ right)), или ( left( text right)) – Герц. Это фамилия Генриха Герца, знаменитого физика.

[displaystyle 1 text = frac = c^ ]

Частота и период связаны обратной пропорциональностью:

Количество оборотов

Двигаясь по окружности достаточное время, тело может пройти не один оборот. Зная угловой путь (varphi ) мы можем вычислить количество N оборотов.

( N ) – количество оборотов, скаляр. Обороты считают поштучно.

Связь между угловой скоростью и частотой

Разделим обе части уравнения на время t, в течение которого тело вращалось

Левая часть уравнения – это угловая скорость.

А дробь в правой части – это частота

Таким образом, мы получили связь между угловой скоростью и частотой

Примечание: Решая задачи на равноускоренное движение по окружности, удобно переходить от частоты к угловой скорости. Тогда можно будет применять аналогию с формулами для равноускоренного движения по прямой.

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Понятия и определения

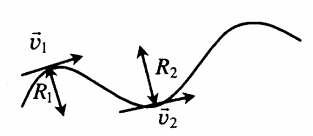
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алиса Никитина | Просмотров: 22.1k

Человек регулярно сталкивается с разными видами движения. Перемещение тела по окружности позволяет понять многие физические процессы. На основе закономерностей такого явления работают разнообразные механизмы. Рассчитать характеристики движения по окружности достаточно просто, если знать и уметь применять несколько основных формул.

Движение тела по окружности — какими законами описывается

Движением по окружности в теории называют вращение какой-либо материальной точки или тела относительно оси, неподвижной в выбранной системе отсчета и не проходящей через центр тела.

Тело может двигаться по окружности двумя способами:

• равномерно;
• неравномерно.

Равномерное движение тела характеризуется постоянной угловой скоростью. Для описания такого перемещения применяют следующие формулы:

• угловая скорость: (omega =frac{2pi }{T})
• скорость движения: (V =frac{2pi R}{T}=omega R)
• угол поворота: (phi =2pi frac{t}{T}=omega t)
• ускорение: (frac{2pi v}{T}=omega ^{2}R)

Неравномерное движение возможно при переменной угловой скорости тела. В данном случае применимы формулы:

• тангенциальное ускорение: (a_{t}=frac{dv}{dt})
• центростремительное ускорение: (a_{n}=frac{v^{2}}{R}=omega ^{2}R)

В представленных уравнениях используются такие параметры, как:

• Т — период вращения;
• t — время;
• ω — угловая скорость;
• R — радиус;
• a_t — тангенциальное ускорение;
• a_n — центростремительное или полное ускорение.

При отсутствии специальных оговорок, в процессе решения задач движение тела по окружности принимают за равномерное. Для расчета пройденного пути используют формулу:

(S=frac{v}{t})

где:

• S является расстоянием, которое преодолело тело;
• v представляет собой скорость движения тела;
• t определяет время движения.

Таким образом, справедливы выражения:

(v=frac{S}{t})

(t =frac{v}{S})

Величины, которые применяют для решения задач, характеризуются положительными значениями:

S > 0, v > 0, t > 0

При решении задач принято все величины переводить в единицы измерения, согласно системе СИ.

Секретом заданий на движение тела по окружности является то, что обгоняющий будет преодолевать на 1 круг больше при первом обгоне. Данное расстояние считается на n кругов больше, если первый объект обогнал другого в n-ый раз.

Задачи на движение по окружности от простых до сложных

Задачи на движение тела по окружности отличаются по степени сложности. Можно рассмотреть примеры простых заданий.

Задача 1

Длина круговой трассы составляет 8 километров. Из ее точки в один момент времени в одинаковом направлении выехали два автомобиля. Первый автомобиль развил скорость 114 км/ч и, спустя 20 минут после начала движения, обогнал второй автомобиль на один круг. Требуется определить скорость, с которой двигался второй автомобиль. Ответ необходимо представить в км/ч.

Решение

Известно, что старт произошел одновременно для обоих автомобилей. Через 20 минут после начала движения первое транспортное средство опережало второе на один круг. Таким образом, в течение 20 минут или 1/3 часа первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.

Ответ: второй автомобиль двигался со скоростью 90 км/ч.

Задача 2

Из пункта А круговой трассы выехал велосипедист, а спустя полчаса стартовал мотоциклист. Через 10 минут после начала пути водитель мотоцикла догнал велосипедиста в первый раз. Спустя еще 30 минут мотоциклист догнал велосипедиста повторно. Требуется определить, какова скорость мотоциклиста, в том случае, когда длина трассы составляет 30 км. Ответ необходимо представить в км/ч.

Решение

В первую очередь требуется перевести минуты в часы. Скорости мотоциклиста и велосипедиста можно обозначить х и у. В первый раз водитель мотоцикла обогнал велосипедиста, спустя 10 минут или 1/6 часа после начала движения. До этого момента велосипедист находился в движении 40 минут или 2/3 часа.

Можно упростить запись условий задачи:

велосипедист: v = х, t = 2/3, S = 2/3*х;

мотоциклист: v = у, t = 1/6, S = 1/6*у.

Велосипедист и мотоциклист преодолели одинаковый путь:

(frac{1}{6}y=frac{2}{3}x)

Спустя 30 минут или 1/2 часа после первого обгона мотоциклист выполнил второй обгон велосипедиста.

Таким образом:

велосипедист: v = х, t = 1/2, S = 1/2*х;

мотоциклист: v = у, t = 1/2, S = 1/2*у.

Требуется определить расстояния, которые преодолели гонщики. Мотоциклист обогнал велосипедиста, то есть проехал больше на один круг. Это является ключевым моментом в данной задаче. Один круг составляет 30 километров. Второе уравнение будет иметь вид:

(frac{1}{2}y-frac{1}{2}x=30)

Далее необходимо решить полученную систему:

у = 4х

у – х = 60

Таким образом, х = 20, у = 80.

Ответ: скорость мотоциклиста равна 80 км/ч.

Бывают задания на движение тела по окружности с повышенной степенью сложности. Как правило, подобные примеры при невозможности проведения экспериментов требуют сложных вычислений.

Задача 3

На часах со стрелками время 8 часов 00 минут. Требуется определить, через сколько минут минутная стрелка в четвертый раз догонит часовую стрелку.

Решение

Спустя один час минутная стрелка преодолевает один круг, а часовая проходит лишь 1/12 циферблата. Допустим, что скорости равны 1 круг в час и 1/12 круга в час соответственно. Начало движения приходится на 8.00. Необходимо определить время, в течение которого минутной стрелке в первый раз удастся догнать часовую.

Минутная стрелка преодолеет на 2/3 круга больше. Исходя из этого, можно записать уравнение:

(1*t-frac{1}{12}t=frac{2}{3})

Таким образом, спустя 8/11 часа стрелки совпадут. Предположим, что через время z стрелки совпадут повторно. Минутная стрелка преодолеет расстояние 1*z, а часовая 1/12*z. При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение:

(1*z-frac{1}{12}z=1)

Решение данного уравнения будет таким:

(z=frac{12}{11})

Таким образом, через 12/11 часа стрелки совпадут повторно. Спустя еще 12/11 часа они встретятся вновь и так далее. Поэтому при старте в 8.00 в четвертый раз минутная стрелка догонит часовую через:

(frac{8}{11}+3frac{12}{11}) часа

Ответ: минутная и часовая стрелки совпадут в четвертый раз через (frac{8}{11}+3frac{12}{11})часа.

Нередко при решении задач на движение по окружности требуется рассчитать среднюю скорость тела. Важно, что данная величина не совпадает со средним арифметическим скоростей. Средняя скорость определяется с помощью формулы:

(v=frac{S_{0}}{t_{0}})

где v является средней скоростью;

S₀ представляет собой общий путь;

t₀ определяет общее время.

При наличии двух участков пути средняя скорость рассчитывается по формуле:

(v=frac{S_{1}+S_{2}}{t_{1}+t_{2}})

Наиболее сложными задачами считаются примеры с пятизначными дискриминантами. Рассмотрим алгоритм действий в таком случае.

Задача 4

Пара гонщиков участвует в соревновании. Путь, который требуется преодолеть, равен 60 кругам кольцевой трассы в 3 км. После одновременного старта первый гонщик пересек финиш раньше, чем второй на 10 минут. Требуется рассчитать среднюю скорость второго гонщика. Известно, что впервые первый участник обогнал второго на круг, спустя 15 минут после начала движения. Ответ требуется записать в км/ч.

Решение

Первый участник гонки, находясь в движении 15 минут, догнал второго гонщика на первом круге. Таким образом, в течение 15 минут он преодолел на 1 круг или на 3 км больше, чем второй. За час первый гонщик проехал 3*4=12 километров больше. При этом скорость его движения на 12 км/ч превышает скорость второго гонщика. 10 минут соответствует ¼ часа. Можно записать уравнение:

(frac{180}{x}-frac{180}{x+12}=frac{1}{6})

Далее необходимо преобразовать выражение к квадратному уравнению:

(x^{2}+12x-12960=0)

Таким образом, получен пятизначный дискриминант. Есть более простой вариант решения задачи. Можно записать уравнение:

(frac{180}{x}-frac{180}{x+12}=frac{1}{6})

В нем 180 можно поделить на 12. Заменим х=12z:

(frac{180}{12z}-frac{180}{12z+12}=frac{1}{6})

(frac{15}{z}-frac{15}{z+1}=frac{1}{6})

(frac{90}{z}-frac{90}{z+1}=1)

Данное равенство можно преобразить в квадратное уравнение. Целый положительный корень такого выражения z=9. Тогда получим:

(х=12z=108)

Ответ: средняя скорость второго гонщика равна 108 км/ч.

Нахождение линейной скорости при движении по окружности

Любая точка, находящаяся на окружности, перемещается с некоторой скоростью. Данная величина называется линейной скоростью. Вектор линейной скорости всегда совпадает по направлению с касательной к окружности. К примеру, стружка из точильного станка движется, повторяя направление мгновенной скорости.

Можно рассмотреть какую-то точку на окружности, совершившую один оборот. При этом было затрачено время равное периоду Т. Расстояние или путь, пройденный точкой, представляет собой длину рассматриваемой окружности.

Задачи на тему равномерное движение по окружности

Задача 1

Радиус выпуклого моста равен 90 м. Требуется определить скорость, с которой автомобиль должен пройти его середину, чтобы пассажир на мгновение ощутил невесомость.

Решение

Согласно условиям задачи:

R = 90 м

N = 0

Сила реакции опоры обладает нулевым значением, так как пассажир в состоянии невесомости не оказывает давление на сиденье автомобиля.

Решение задачи необходимо представить в системе отсчета, которая связана с Землей. Человек совершает движение вместе с автомобилем. Ускорение при этом направлено вниз. На пассажира действует сила притяжения Земли, которая будет центростремительной:

(mg=mfrac{v^{2}}{R})

Таким образом:

(v=sqrt{frac{Rmg}{m}}=sqrt{Rg}=sqrt{90*10}=30) м/с

Ответ: скорость автомобиля составляет 30 м/с.

Задача 2

Масса девочки 40 кг. Она качается на качелях, длина подвеса которых составляет 4 м. Требуется определить силу, с которой девочка давит на сиденье при прохождении среднего положения со скоростью 5 м/с.

Решение

На девочку действует сила тяжести (mvec{g}) и сила реакции опоры (vec{N}).

Качели находятся под действием силы давления  (vec{F_{g}}), которая направлена вниз. Согласно третьему закону Ньютона, данная сила соответствует взятой со знаком минус силе реакции опоры:

(vec{F_{g}}=-vec{N})

Таким образом, решением задачи является определение силы реакции опоры. Исходя из закона динамики:

(mvec{g}+vec{N}= mvec{a})

В проекции на ось Х:

(N-mg=mfrac{v^{2}}{R})

Из чего следует вывод:

(F_{g}=left|N right|=m(g+frac{v^{2}}{R}))

(F_{g}=40(10+frac{5^{2}}{4})=650) Н

Ответ: сила равна 650 Н.

Задача 3

Шарик привязали с помощью нити к подвесу. Он описывает в горизонтальной плоскости окружность, совершая движение с постоянной скоростью. Нить обладает длиной 0,6 м и составляет с вертикалью угол в 60 градусов. Необходимо рассчитать, какова скорость шарика.

Решение

Сумма сил (mvec{g}) и натяжения (vec{F_{n}}), исходя из правила параллелограмма, соответствует результирующей силе, направленной в центр вращения (sum_{i}^{}{vec{F}_{i}}):

(sum_{i}^{}{vec{F}_{i}}= mvec{g}+vec{F_{n}}= mvec{a})

Силы в сумме определяются из прямоугольного треугольника с углом α равным 60 градусам. Исходя из того, что (vec{F_{n}}) является противолежащим катетом, получим:

(vec{F_{n}}=mg*tg α)

Таким образом:

(mg*tg α= mvec{a}= mfrac{v^{2}}{R})

(v^{2}=frac{mg*tan alpha *R}{m}=gR*tan alpha)

R включен в прямоугольный треугольник, в котором длина нити представляет собой гипотенузу. R является катетом, противолежащий углу α в 60 градусов.

(R=l*sin alpha)

Преобразив формулу квадрата скорости шарика с помощью подстановки выражения для радиуса, получим:

(v^{2}=gl*sin alpha *tan alpha )

(v=sqrt{gl*sin alpha *tan alpha }=sqrt{10*0.6*frac{sqrt{3}}{2}*sqrt{3}}=3) м/с

Ответ: скорость шарика составляет 3 м/с.

Задача 4

Необходимо определить максимальную скорость мотоцикла по горизонтальной плоскости, который описывает при этом дугу окружности с радиусом 100 м. Коэффициент трения резины о плоскость составляет 0,4.

Решение

Во время поворота мотоцикл наклоняется к центру поворота. На транспортное средство оказывают действие:

• сила тяжести (mvec{g});
• сила реакции опоры (vec{N});
• сила трения (vec{F_{tr}});
• сила тяги (vec{F_{t}});
• сила сопротивления (vec{F_{c}}).

Данные силы в сумме составляют:

(mvec{g}+vec{N}+vec{F_{tr}}+vec{F_{t}}+vec{F_{c}}= mvec{a})

Согласно выражениям:

(mvec{g}+vec{N}=0)

(vec{F_{t}}+vec{F_{c}}=0)

Получим:

(vec{F_{tr}}= mvec{a})

Сила трения составляет:

(F_{tr}= mu mg)

Таким образом:

(mu mg=ma= mfrac{v^{2}}{R})

(v=sqrt{frac{mu mgR}{m}}=sqrt{mu gR}=sqrt{0.4*10*100}=20) м/с

Ответ: максимальная скорость равна 20 м/с.

Задачи разной сложности по теме движения тела по кружности часто встречаются не только в школьной программе, но и во время обучения в вузе. Знание основных закономерностей позволит быстро найти решение примера любой сложности. Если в процессе расчетов возникают трудности, всегда можно обратиться за помощью к сервису Феникс.Хелп.

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

Равномерное движение по окружности:

На предыдущих уроках вы ознакомились с различными видами прямолинейного движения, с величинами, характеризующими эти движения, и определили, как изменяются эти величины со временем.

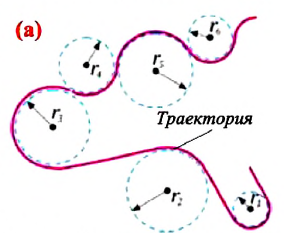
Наиболее простой вид криволинейного движения — это широко распространенное в природе и технике движение по окружности. Вращение точек поверхности Земли вокруг своей оси, точек часовых стрелок, точек автомобильных колес и др. является движением по окружности. Теоретическая и практическая важность изучения движения по окружности заключается в том, что произвольную криволинейную траекторию можно представить как сумму дуг окружностей разных радиусов (а). Самый простой вид движения по окружности — это равномерное движение.

• Равномерное движение по окружности — это движение, при котором модуль скорости материальной точки в каждой точке этой окружности остается неизменным. Такое движение характеризуется следующими величинами:

Период обращения — это время, затраченное на один полный оборот материальной точки по окружности:

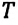
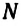
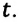
Где  — период обращения, — число полных оборотов материальной точки за время За единицу периода обращения в СИ принята секунда:

Частота обращения — это число оборотов материальной точки по окружности, совершаемых за единицу времени:

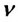
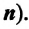
Где — частота обращения (иногда обозначается буквой За единицу частоты обращения в СИ принят 1 герц — частота такого обращения, когда тело за секунду совершает один полный оборот:

Период и частота обращения обратно пропорциональны друг другу:

Это означает, что во сколько раз уменьшится частота обращения, во столько же раз увеличится период обращения, и наоборот.

Угол поворота — это угол, на который поворачивается радиус-вектор при движении материальной точки по окружности. Угол поворота измеряется отношением длины дуги окружности между начальным и конечным радиус-векторами к радиусу окружности (b):

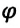
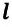
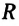
Где  — угол поворота, — длина дуги, соответствующая углу поворота,  — радиус окружности. Углы поворота радиус-вектора материальной точки, движущейся равномерно по окружности, за равные промежутки времени одинаковы.

Угол поворота является скалярной величиной, единица его измерения в СИ — радиан:

• 1 рад — это угол поворота радиус-вектора, соответствующий дуге, длина которой равна радиусу окружности

Угловая скорость — это физическая величина, измеряемая отношением угла поворота к промежутку времени, за которое этот поворот совершен:

Угловая скорость материальной точки, равномерно движущейся по окружности, с течением времени остается неизменной 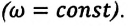 Единица угловой скорости в СИ — радиан в секунду:

За единицу угловой скорости принята угловая скорость такого равномерного движения по окружности, при котором за 1 секунду радиус-вектор материальной точки поворачивается на угол в 1 радиан.

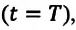
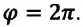
Материальная точка, движущаяся равномерно по окружности, за время, равное периоду обращения совершает один полный оборот, за это время радиус-вектор поворачивается на угол  Поэтому при равномерном движении по окружности между угловой скоростью и периодом обращения (частотой обращения) имеется связь:

Линейная скорость. Скорость движения материальной точки по окружности называется линейной скоростью. Линейная скорость материальной точки, равномерно движущейся по окружности, оставаясь постоянной по модулю 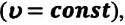непрерывно изменяется по направлению и в любой точке направлена по касательной к траектории (с).

Численное значение линейной скорости при равномерном движении по окружности равно отношению пройденного пути ко времени, затраченному на его прохождение:

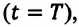
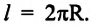
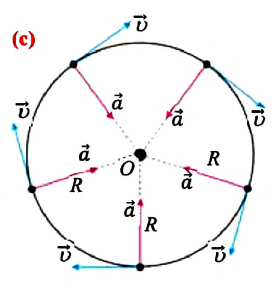
Материальная точка, двигаясь равномерно по окружности, за время, равное периоду обращения проходит путь, равный длине круга: Приняв это во внимание в формуле линейной скорости, получим выражение, связывающее линейную скорость с угловой скоростью:

Центростремительное ускорение:

Быстрота изменения направления линейной скорости при равномерном движении по окружности характеризуется физической величиной называемой центростремительным, или нормальным, ускорением. Вектор центростремительного, или нормального, ускорения в любой точке траектории направлен по радиусу к центру окружности (см.: с). Модуль центростремительного ускорения материальной точки при равномерном движении по окружности равен отношению квадрата линейной скорости к радиусу окружности: