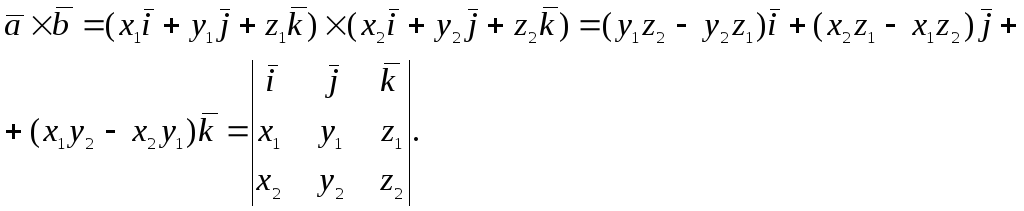Как найти длину ребра через векторы

Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)

Краткая теория

---

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды 
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

 найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

Угол между ребрами

 и

 найдем как угол
между направляющими векторами

  и

:

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

 и гранью

.

Для этого вычислим
координаты нормального вектора плоскости

 –им будет
векторное произведение векторов 

 и

.

 

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

  

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

    и 

:

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

  и

:

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

.  Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

 

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

 -уравнение
грани

 

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

 из вершины

:

Нормальный вектор

 является
направляющим вектором высоты, кроме того, высота проходит через точку

 

Искомое уравнение
высоты:

Сделаем схематический чертеж:

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Длина ребра через вектор

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

По координатам вершин пирамиды найти

Дата добавления: 2015-01-16 ; просмотров: 15047 ; Нарушение авторских прав

Даны координаты пирамиды: A(4,2,5), B(-3,5,6), C(2,-3,-2), D(9,4,18)
1) Координаты векторов.
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i; Z = z_j — z_i
здесь X,Y,Z координаты вектора; x_i, y_i, z_i — координаты точки А_i; x_j, y_j, z_j — координаты точки А_j;
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁; Z = z₂ — z₁
X = -3-4; Y = 5-2; Z = 6-5
AB(-7;3;1)
AC(-2;-5;-7)
AD(5;2;13)
BC(5;-8;-8)
BD(12;-1;12)
CD(7;7;20)

2) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:

3) Угол между ребрами.
Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂
Найдем угол между ребрами AB(-7;3;1) и AC(-2;-5;-7):

γ = arccos(0.118) = 96.775 0

4) Площадь грани
Площадь грани можно найти по формуле:

где

Найдем площадь грани ABC
Найдем угол между ребрами AB(-7;3;1) и AC(-2;-5;-7):

Площадь грани ABC

Найдем площадь грани с учётом геометрического смысла векторного произведения:

Векторное произведение:

= i(3 • (-7)-(-5) • 1) — j((-7) • (-7)-(-2) • 1) + k((-7) • (-5)-(-2) • 3) = -16i — 51j + 41k

X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3

Находим определитель матрицы
∆ = (-7) • ((-5) • 13-2 • (-7))-(-2) • (3 • 13-2 • 1)+5 • (3 • (-7)-(-5) • 1) = 351
7) Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂), представляется уравнениями:

Уравнение прямой AD(5,2,13)

Уравнение плоскости.
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости ABC

(x-4)(3 • (-7)-(-5) • 1) — (y-2)((-7) • (-7)-(-2) • 1) + (z-5)((-7) • (-5)-(-2) • 3) = -16x — 51y + 41z-39 = 0

10) Длина высоты пирамиды, проведенной из вершины D(9,4,18)
Расстояние d от точки M₁(x₁;y₁;z₁) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:

Уравнение плоскости ABC: -16x — 51y + 41z-39 = 0

11) Уравнение высоты пирамиды через вершину D(9,4,18)
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости ABC: -16x — 51y + 41z-39 = 0

Пример 1:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

Сделать чертеж.

А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Решение от преподавателя:

Пример 2:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

 Уравнение плоскости. 
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-3)(1*2-0*3) — (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y — 3z-38 = 0 

Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.267) = 15.486^o 

Уравнение высоты пирамиды через вершину A₄(0,2,2) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 

Уравнение плоскости через вершину A₄(0,2,2) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
2(x-0)+13(y-2)-3(z-2) = 0 
или 
2x+13y-3z-20 = 0

Пример 4:

Решение от преподавателя:

Даны координаты пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 

1. Уравнение плоскости. 
   Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

(x-0)(3*2-8*3) — (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x — 15y + 33z-18 = 0 
Упростим выражение: -6x — 5y + 11z-6 = 0 

2) Угол между прямой A₁A₄ и плоскостью A₁A₂A₃. 
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.193) = 11.128^o 

3) Уравнение высоты пирамиды через вершину A₄(0,5,4) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 

4) Уравнение плоскости через вершину A₄(0,5,4) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости

5)  Координаты вектора  A₁A₄(0;4;3) 

Уравнение прямой, проходящей через точку А₁(0,1,1) параллельно вектору А₁А₂(0,4,3) имеет вид:

Пример 5:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

1) Даны координаты  вершин пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 
Координаты векторов. 
Координаты векторов:       A₁A₂(3;3;3)        A₁A₄(0;4;3) 

 Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   ,    где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
Найдем угол между ребрами A₁A₂(3;3;3) и A₁A₃(0;4;3): 

А₁ = arccos(0,808)

Найдем площадь грани с учётом геометрического смысла векторного произведения: 
S =
Найдем векторное произведение

=i(3*2-8*3) — j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i — 15j + 33k 

3) Объем пирамиды. 
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

Координатывекторов:A₁A₂(3;3;3)    A₁A₃(-3;8;2) A₁A₄(0;4;3) :      

Пример 7:

Решение от преподавателя:

1. Угол между ребрами. 
   Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   
   где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   γ = arccos(0) = 90.003⁰ 
2. Площадь грани 
   Площадь грани можно найти по формуле: 
   
   где 
   
   Найдем площадь грани A₁A₂A₃ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   
   Площадь грани A₁A₂A₃ 
3. Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

где определитель матрицы равен: 
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18 

Пример 8:

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Решение от преподавателя:

1) Длина ребра A₁A₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁А₂А₃;

Найдем уравнение стороны А₁А₄:

Вектор нормали:  к плоскости А₁А₂А₃.

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

Итак: z=4 – уравнение плоскости А₁А₂А₃.

уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

A₄O – высота:

Уравнение A₄O:

Т.к. , то

В результате получаем уравнение высоты:

Пример 9:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Любой вектор в декартовой системе координат может быть представлен в виде

Где координаты вектора Орты координатных осей.

Вектор с началом в точке и концом в точке Имеет вид:

,

то есть .

Длина отрезка называется Длиной (модулем) вектора, обозначается = и вычисляется по формуле

.

Сумма векторов и определяется формулой

Произведение вектора На число определяется формулой

.

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т. е.

.

Скалярное произведение векторов и вычисляется по формуле:

.

Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:

1) длина вектора равна площади параллелограмма, построенного на векторах и , т. е. ;

2) вектор перпендикулярен векторам и ;

3) векторы образуют правую тройку, то есть они ориентированы по отношению друг к другу соответственно как орты .

Модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на этих векторах:

Векторное произведение векторов и вычисляется по формуле:

.

Смешанным произведением векторов называется скалярное произведение вектора на вектор , то есть .

Модуль смешанного произведения векторов численно равен объему параллелепипеда, построенного на этих векторах:

Пусть Тогда

.

Уравнение любой плоскости может быть записано в виде:

где .

Вектор , перпендикулярный плоскости, называется Нормальным Вектором плоскости.

Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

Угол между плоскостями и определяется следующим образом:

.

Расстояние от точки До плоскости, определяемой уравнением , находится по формуле

.

Прямая В пространстве может быть задана уравнениями двух плоскостей

,

Пересекающихся по этой прямой, или Каноническими уравнениями прямой

,

Которые определяют прямую, проходящую через точку и параллельную вектору . Вектор называется Направляющим вектором прямой.

Уравнения прямой, проходящей через две точки и , имеют вид:

.

Угол между Двумя прямыми и определяется следующим образом:

.

Угол между прямой и плоскостью определяется следующим образом:

.

Если Точка Делит отрезок АВ, где ,, в Отношении, то координаты точки М определяются по формулам:

.

Задание 1. Даны координаты вершин пирамиды : , . Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой ; 7) уравнение плоскости ; уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Решение. 1) Для определения длины ребра найдем координаты вектора : . Тогда длина ребра будет равна длине вектора :

.

2) Найдем угол между ребрами и . Для этого, как и раньше, найдем координаты вектора , определяющего ребро . Получим и .

Тогда угол между ребрами и можно найти из определения скалярного произведения двух векторов:

.

Следовательно, .

3) Чтобы найти угол между ребром и гранью , определим нормальный вектор Плоскости . Из определения векторного произведения двух векторов имеем:

,

Т. е. и . Тогда , .

Так как нормальный вектор перпендикулярен плоскости , то угол между ребром и гранью определяется как .

4) Площадь грани можем найти по формуле . Следовательно, Кв. ед.

5) Объем пирамиды, построенной на векторах, равен 1/6 объема параллелепипеда, построенного на этих же векторах. Для определения объема параллелепипеда воспользуемся свойством смешанного произведения векторов. В результате имеем:

Таким образом, куб. ед.

6) Составим уравнения прямой . Для этого воспользуемся уравнениями прямой, проходящей через две заданные точки И :

.

Получаем:

.

7) Уравнение плоскости можно найти по формуле:, где , . Следовательно, уравнение плоскости имеет вид: или после упрощения .

Чтобы составить уравнение высоты , опущенной из вершины на грань , воспользуемся формулой:

,

Где , — направляющий вектор высоты Пирамиды . Так как вектор Перпендикулярен грани , то в качестве Можно взять вектор — нормальный вектор плоскости .

Следовательно, имеем: или .

9) Сделаем теперь чертеж:

< Предыдущая		Следующая >

§1. Векторная алгебра

1.
Определение. Линейные операции. Базис.
Вектором

называется направленный отрезок в
пространстве (на плоскости). Вектор
имеет две характеристики: длину,
называемую также модулем и обозначаемую

,
и направление. Принято также вектор
обозначать двумя буквами, первая из
которых указывает начало вектора, вторая
– конец:
.

Два
вектора считаются равными,
если они:

1)
равны по длине; 2) лежат на параллельных
прямых; 3) сонаправлены. Вектор, имеющий
нулевую длину (т.е. у которого совпадают
начало и конец), называется нуль-вектором,
или нулевым вектором, и обозначается
0.
Нуль-вектор считается параллельным
любому вектору. Вектор, модуль которого
равен единице, называется единичным
вектором, или ортом.

Суммойвекторов
иназывается вектор,
определяемый по правилу: если путём
параллельного переноса совместить
начало векторас концом вектора,
то начало векторасовпадает с началом,
а конец– с концом;
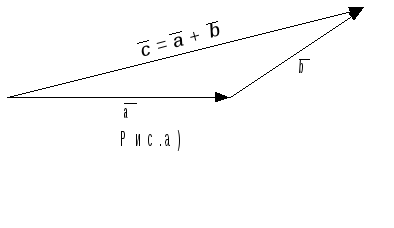
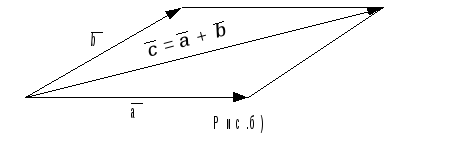
при этом пишут(рис. а). Векторы можно складывать и по
«правилу параллелограмма» (рис. б). Если
слагаемых больше, то используют правило
замыкания ломаной (рис.в) .

Справедливо правило
уничтожения средней буквы:

.

Произведением
вектора

на действительное число
называется
вектор, обозначаемый
,
или,
и удовлетворяющий следующим требованиям:

1)
;
2)ипараллельны; 3)исонаправлены прии направлены в противоположные стороны
при.

Линейные
операции удовлетворяют следующим
свойствам:

1)
+=+– коммутативность.

2)
+ (+)
= (+)+

3)
+=

4)
+(-1)=

5)
()=()
– ассоциативность

6)
(+)=+– дистрибутивность

7)
(+)
=+

1=

Единичный
вектор,
параллельный
и сонаправленный с ним, называется ортом
вектораи обозначается;.

Векторы
,называютсяколлинеарными,
если они лежат на одной прямой (или на
параллельных прямых). Векторы
,
лежащие в одной плоскости (или в
параллельных плоскостях), называюткомпланарными.

Рассмотрим
систему векторов

.

Система
векторов

называется линейно
зависимой,
если существуют числа
,
не все равные нулю и такие, что.
Если же равенствовозможно лишь при,
то система векторовназываетсялинейно
независимой.

Теорема
1. а) Векторы
коллинеарны в том и только в том случае,
если они линейно зависимы; б) векторыкомпланарны в том и только в том случае,
если они линейно зависимы.

Упорядоченная
тройка
(двойка)
некомпланарных (неколлинеарных) векторов
пространства (плоскости) называетсябазисом
во множестве всех векторов пространства
(плоскости). Любой вектор
в пространстве может быть представлен
в виде линейной комбинации векторов
базиса:

.

Более
того, такое представление единственно;
числа
называютсякоординатами
вектора
в базисе.

Последнее
означает, что координаты вектора
однозначно определяют сам вектор. Иначе
говоря, упорядоченную тройку чисел
можно считать вектором в фиксированном
базисе. В связи с этим можно записать
следующиесвойства:

равные
векторы имеют одинаковые координаты;

при
умножении вектора на число его компоненты
тоже умножаются на это число, т.е.

=
;

при
сложении векторов складываются их
соответствующие компоненты:

;

;

+
=.

Векторы
иколлинеарны в том и только в том случае,
если координаты этих векторов (в
произвольном базисе) пропорциональны.

Если
векторы
единичные и взаимно перпендикулярны,
то они образуют базис, который называетсяортонормированным.

Типовой
пример. Найти
орт вектора
.

►,

.
Тогда
.◄

Если

,

,
то условие
коллинеарности
векторов
и– это пропорциональность координат.

Типовой
пример.
Дано:
,,.
Есть ли среди них коллинеарные?

►Проверяя
условие коллинеарности
двух векторов попарно, получаем, чтоколлинеарен,
коэффициент пропорциональности их
координат равен (-2).◄

Типовой
пример.
Дано: точки
,

,
число
.
Найти точку
,
которая делила бы отрезок

в отношении
.

►Так
как отрезок
делится
точкой М в отношении
,
это означает, что
.
Координаты
,
координаты
.
Значит,
.
Откуда получаем:
.
Т.е. точка
==;=.

В
частности, если М – середина отрезка
АВ, то

.◄

Типовой
пример. Дан
треугольник
,
где
,

,.

Найти
координаты точки
–пересечения
биссектрисы угла
со стороной.

►,
,

,

.

.

;

;

Итак,
.
◄

Упорядоченная
тройка некомпланарных векторов
образуетправую
(левую)
тройку, если после совмещения их начал
путём параллельного переноса кратчайший
поворот от первого вектора
ко второму векторувиден из конца третьего векторасовершающимся против (по) часовой
стрелки.

Для
ортонормированного базиса
,
образующего правую тройку, приняты
обозначения.

Проекцией
вектора
на вектор(или на ось, параллельную и сонаправленную)
называют число,
где
– угол между векторами
и.
В ортонормированном базисе координатыX,
Y
, Z
вектора
совпадают с его проекциями на базисные
орты
:
при этом .

Обозначим
через
углы между вектороми векторами

соответственно. Числа
называютсянаправляющими
косинусами
вектора
.
Имеют место формулы:

,
,

Часто
краткости ради вместо
пишут.
Аналогичные определения приняты на
множестве векторов плоскости.

Теорема
2. Тройка
векторов
,,образует базис в том и только в том
случае, если

.

Типовой
пример.
Доказать, что векторы
,,
образуют базис. Найти разложение векторав этом базисе.

►Имеем

.

Следовательно,
векторы
образуют базис. КоординатыX,
Y,
Z
вектора
в этом базисе должны удовлетворять
равенству,
или в матричной записи

.

Это
приводит к системе линейных алгебраических
уравнений

Решив
эту систему, найдём X
= 2, Y
= 1, Z
= 1. Таким образом,
.◄

Прямоугольная
система координат
в пространстве задаётся точкой 0 –
началом координат – и ортонормированным
базисом
.

Оси
0x,
0y,
0z,
проведённые через точку 0 параллельно
векторам
,
называются координатными
осями.

Каждой
точке M
пространства ставится в соответствие
вектор
,
называемыйрадиус-вектором
точки M;
это соответствие является взаимно-однозначным.
Координатами x
, y
, z
точки M
называются координаты её радиус-вектора

Координаты вектора
выражаются через координаты началаи концавектора по формулам,,.

Расстояние
между точками
ивыражается формулой.

2. Скалярное
произведение и его приложения.
Скалярным произведением
двух векторов
иназывают
число, определяемое формулой.
(1)

Скалярное
произведение обладает следующими
свойствами:

1)

2)

3)

4)
,.

Из
(1) также следует, что

прпр.
(2)

Число,
равное
,
называетсяскалярным
квадратом
вектора
.
Скалярный квадрат вектора равен квадрату
его длины.
Действительно,

.

Рассмотрим
ортонормированный базис
Очевидно,

.
(3)

Используя
свойства скалярного произведения и
учитывая (3), легко найти выражение
скалярного произведения через координаты
перемножаемых векторов в ортонормированном
базисе.

Теорема.
Если
,
то

(4)

Если
то из (4) найдем, что

Отсюда
следует формула косинуса угла между
векторами
и;

,
т.е.
.

Условие
перпендикулярности:
в том и только в том случае, если

Типовой
пример. Даны
точки: А(2;1;4),
В(0;-1;2),
С(4;3;-2).
Требуется: а) найти координаты вектора
;

б) найти угол
.

►а)
Найдем координаты вектора
:
из координат конца (точкаВ)
вычтем координаты начала (точка А):
.
Найдем координаты вектора:.
Найдем координаты вектора:

.

Найдем
координаты вектора
:

.

б) Найдем длины
векторов
ипо формуле.

Получаем:

,

.

Для
нахождения угла воспользуемся формулой

;

.

Ответ:

;.◄

Типовой
пример. Даны
точки A(–2; 1; 3), B(0;
–1; 2), C(3;
–2; 1).

Найти:
а) длину отрезка АВ; б) косинус угла B
в треугольнике АВС;
в)
;
г)
и направляющие косинусы.

►а)
;

б)
угол В в треугольнике АВС есть угол
между векторами
и.
Имеем,,
,
,

;

в)

,
,

,

,

отсюда
находим

;

г)
.

Направляющими
косинусами вектора
являются 2/3, –2/3, –1/3.

Типовой
пример.
Дано:
,,,.
Найти угол между векторамии.

►
Так как
или.

,

,

Таким
образом,
.
◄

Типовой
пример.
Найти длину вектора
,
если,,.

►

◄

3.
Векторное произведение и его свойства.
Векторным
произведением
упорядоченной пары неколлинеарных
векторовиназывается вектор,
удовлетворяющий следующим трём
требованиям:

1),
где
– угол между векторами
и;

2)

перпендикулярен каждому из векторови;

3)

образуют правую тройку.

Векторное
произведение принято также обозначать
.

Свойства
векторного произведения

1)
векторы

и
– коллинеарны;

2)

(антикоммутативность);

3)
,


(однородность);

4)
,

(дистрибутивность).

Выражение
векторного произведения через координаты
сомножителей

Найдем
векторные произведения базисных ортов
,
,
.
Результаты можно записать в табл. 1.

Таблица 1

Пользуясь
этой таблицей и свойствами векторного
произведения, легко найти формулу для
выражения векторного произведения
через декартовы координаты сомножителей.

Теорема.
Если
,
то

Типовой
пример. Вычислить
длину стороны АВ и площадь параллелограмма,
построенного на векторах
и,
если

А(3;2;1),
В(-1;0;2),
С(0;-1;1).

►Найдем
координаты вектора
:.
Длина стороныАВ
равна длине
вектора
:

.

Площадь
параллелограмма, построенного на
векторах
и, численно равна длине вектора.
Поскольку(-3;-3;0),
то

.

Т.е.
,
а его длина.
Значит:(кв. ед.).Ответ:
,(кв. ед.)◄

4. Смешанное
произведение векторов.
Смешанным
произведением
трех векторов ,
,

называется число, равное скалярному
произведению вектора
на векторное произведение векторов
и ,
т.е.
.

Геометрический
смысл смешанного произведения выражает
следующая теорема.

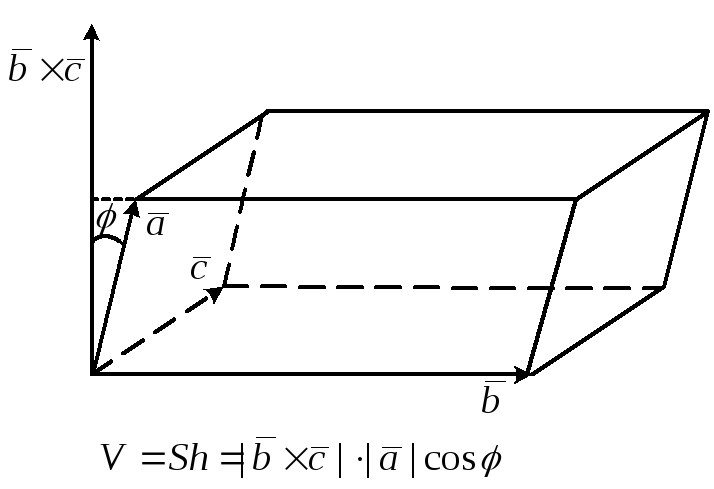
Теорема.
Смешанное
произведение
равно объему
параллелепипеда, построенного на
приведенных к общему началу векторах,
,
,
взятому со
знаком «плюс», если тройка векторов ,
,

правая, и со знаком «минус», если тройка
векторов ,
,

левая. Если же векторы ,
,

компланарны, то
.

В
краткой записи:

Свойства смешанного
произведения

1.

.
Данное равенствопозволяет обозначать смешанное
произведение векторов,
,

символом
,
не указывая при этом, какие именно два
вектора (первые или последние) перемножаются
векторно.

2.
Величина
векторного произведения не изменяется
при циклической перестановке сомножителей:

3.

векторыкомпланарны.

4.
Смешанное
произведение линейно по каждому из
сомножителей. В частности,

.

Выражение
векторного произведения через координаты
сомножителей.

Теорема.
Если векторы
заданы своими координатами:,,,
то смешанное произведение
равняется
определителю, строки которого
соответственно равны координатам
перемножаемых векторов, т.е.

.

Действительно,.Тогда

.

Типовой
пример. Даны
точки A(4;
-1; 3), B(0;
1; 2), C(3;
-2; 5), D(1;
-1; 1). Найти: а) площадь треугольника АВС;
б) высоту
треугольника АВС, опущенную из вершины
А на сторону ВС; в) объём пирамиды АВСD.

►а)
Площадь
треугольника АВС равна половине площади
параллелограммаS,
построенного на векторах
и,
т.е..
Имеем,
,

;

б)

;

,

;

;

в)
Объём
пирамиды АВСD
равен
объёма параллелепипеда, построенного
на векторах.
Имеем,,;

.◄

Типовой пример.
Даны координаты
вершин пирамиды
.

►1)
Найти длину
ребра
.

2)
Найти угол между ребрами
и.

3)
Найти угол между ребром
и гранью.
Сначала найдем вектор нормали к граникак векторное произведение векторови.

=
(2-1;
1-0; 1-3) = (1; 1; -2),

Найдем
угол между вектором нормали и вектором
.

,
-4
– 4 = -8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
– .

.

4)
Найти площадь
грани

.

5)
Найти объем
пирамиды.

(ед³).◄