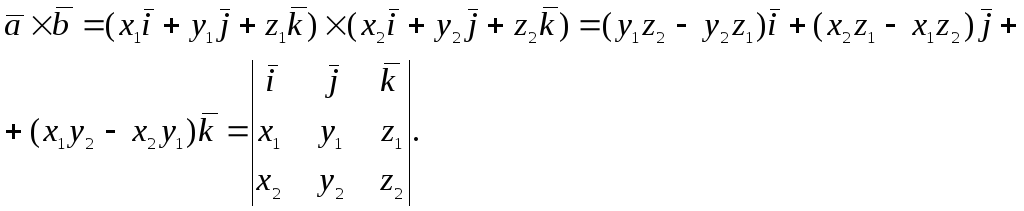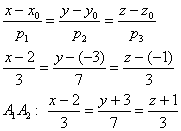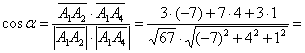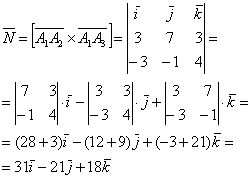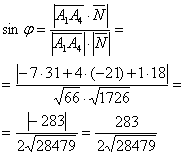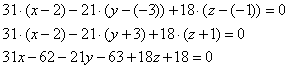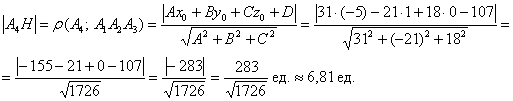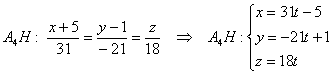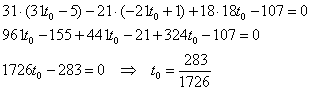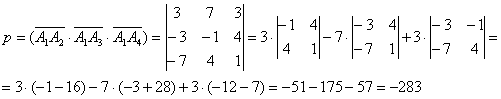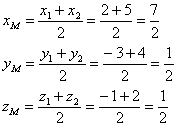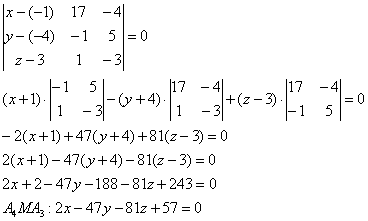Как найти длину ребра треугольника векторы

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

источники:

http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-koordinaty-vershin-piramidy

http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/

Источник

§1. Векторная алгебра

1.
Определение. Линейные операции. Базис.
Вектором

называется направленный отрезок в
пространстве (на плоскости). Вектор
имеет две характеристики: длину,
называемую также модулем и обозначаемую

,
и направление. Принято также вектор
обозначать двумя буквами, первая из
которых указывает начало вектора, вторая
– конец:
.

Два
вектора считаются равными,
если они:

1)
равны по длине; 2) лежат на параллельных
прямых; 3) сонаправлены. Вектор, имеющий
нулевую длину (т.е. у которого совпадают
начало и конец), называется нуль-вектором,
или нулевым вектором, и обозначается
0.
Нуль-вектор считается параллельным
любому вектору. Вектор, модуль которого
равен единице, называется единичным
вектором, или ортом.

Суммойвекторов
иназывается вектор,
определяемый по правилу: если путём
параллельного переноса совместить
начало векторас концом вектора,
то начало векторасовпадает с началом,
а конец– с концом;
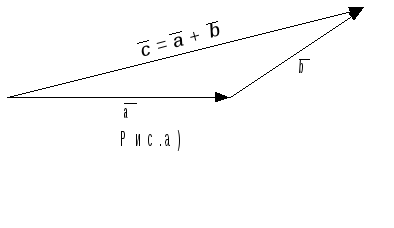
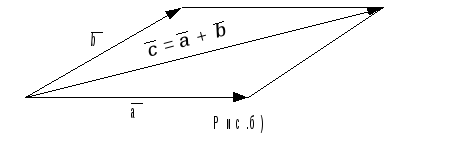
при этом пишут(рис. а). Векторы можно складывать и по
«правилу параллелограмма» (рис. б). Если
слагаемых больше, то используют правило
замыкания ломаной (рис.в) .

Справедливо правило
уничтожения средней буквы:

Произведением
вектора

на действительное число
называется
вектор, обозначаемый
,
или,
и удовлетворяющий следующим требованиям:

1)
;
2)ипараллельны; 3)исонаправлены прии направлены в противоположные стороны
при.

Линейные
операции удовлетворяют следующим
свойствам:

1)
+=+– коммутативность.

2)
+ (+)
= (+)+

3)
+=

4)
+(-1)=

5)
()=()
– ассоциативность

6)
(+)=+– дистрибутивность

7)
(+)
=+

1=

Единичный
вектор,
параллельный
и сонаправленный с ним, называется ортом
вектораи обозначается;.

Векторы
,называютсяколлинеарными,
если они лежат на одной прямой (или на
параллельных прямых). Векторы
,
лежащие в одной плоскости (или в
параллельных плоскостях), называюткомпланарными.

Рассмотрим
систему векторов

Система
векторов

называется линейно
зависимой,
если существуют числа
,
не все равные нулю и такие, что.
Если же равенствовозможно лишь при,
то система векторовназываетсялинейно
независимой.

Теорема
1. а) Векторы
коллинеарны в том и только в том случае,
если они линейно зависимы; б) векторыкомпланарны в том и только в том случае,
если они линейно зависимы.

Упорядоченная
тройка
(двойка)
некомпланарных (неколлинеарных) векторов
пространства (плоскости) называетсябазисом
во множестве всех векторов пространства
(плоскости). Любой вектор
в пространстве может быть представлен
в виде линейной комбинации векторов
базиса:

Более
того, такое представление единственно;
числа
называютсякоординатами
вектора
в базисе.

Последнее
означает, что координаты вектора
однозначно определяют сам вектор. Иначе
говоря, упорядоченную тройку чисел
можно считать вектором в фиксированном
базисе. В связи с этим можно записать
следующиесвойства:

равные
векторы имеют одинаковые координаты;

при
умножении вектора на число его компоненты
тоже умножаются на это число, т.е.

=
;

при
сложении векторов складываются их
соответствующие компоненты:

;

+
=.

Векторы
иколлинеарны в том и только в том случае,
если координаты этих векторов (в
произвольном базисе) пропорциональны.

Если
векторы
единичные и взаимно перпендикулярны,
то они образуют базис, который называетсяортонормированным.

Типовой
пример. Найти
орт вектора
.

►,

.
Тогда
.◄

Если

,
то условие
коллинеарности
векторов
и– это пропорциональность координат.

Типовой
пример.
Дано:
,,.
Есть ли среди них коллинеарные?

►Проверяя
условие коллинеарности
двух векторов попарно, получаем, чтоколлинеарен,
коэффициент пропорциональности их
координат равен (-2).◄

Типовой
пример.
Дано: точки
,

,
число
.
Найти точку
,
которая делила бы отрезок

в отношении
.

►Так
как отрезок
делится
точкой М в отношении
,
это означает, что
.
Координаты
,
координаты
.
Значит,
.
Откуда получаем:
.
Т.е. точка
==;=.

В
частности, если М – середина отрезка
АВ, то

.◄

Типовой
пример. Дан
треугольник
,
где
,

,.

Н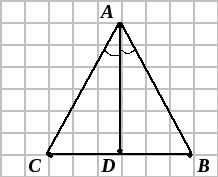айти
координаты точки
–пересечения
биссектрисы угла
со стороной.

►,
,

;

Итак,
.
◄

Упорядоченная
тройка некомпланарных векторов
образуетправую
(левую)
тройку, если после совмещения их начал
путём параллельного переноса кратчайший
поворот от первого вектора
ко второму векторувиден из конца третьего векторасовершающимся против (по) часовой
стрелки.

Для
ортонормированного базиса
,
образующего правую тройку, приняты
обозначения.

Проекцией
вектора
на вектор(или на ось, параллельную и сонаправленную)
называют число,
где
– угол между векторами
и.
В ортонормированном базисе координатыX,
Y
, Z
вектора
совпадают с его проекциями на базисные
орты
:
при этом .

Обозначим
через
углы между вектороми векторами

соответственно. Числа
называютсянаправляющими
косинусами
вектора
.
Имеют место формулы:

,
,

Часто
краткости ради вместо
пишут.
Аналогичные определения приняты на
множестве векторов плоскости.

Теорема
2. Тройка
векторов
,,образует базис в том и только в том
случае, если

Типовой
пример.
Доказать, что векторы
,,
образуют базис. Найти разложение векторав этом базисе.

►Имеем

Следовательно,
векторы
образуют базис. КоординатыX,
Y,
Z
вектора
в этом базисе должны удовлетворять
равенству,
или в матричной записи

Это
приводит к системе линейных алгебраических
уравнений

Решив
эту систему, найдём X
= 2, Y
= 1, Z
= 1. Таким образом,
.◄

Прямоугольная
система координат
в пространстве задаётся точкой 0 –
началом координат – и ортонормированным
базисом
.

Оси
0x,
0y,
0z,
проведённые через точку 0 параллельно
векторам
,
называются координатными
осями.

Каждой
точке M
пространства ставится в соответствие
вектор
,
называемыйрадиус-вектором
точки M;
это соответствие является взаимно-однозначным.
Координатами x
, y
, z
точки M
называются координаты её радиус-вектора

Координаты вектора
выражаются через координаты началаи концавектора по формулам,,.

Расстояние
между точками
ивыражается формулой.

2. Скалярное
произведение и его приложения.
Скалярным произведением
двух векторов
иназывают
число, определяемое формулой.
(1)

Скалярное
произведение обладает следующими
свойствами:

4)
,.

Из
(1) также следует, что

прпр.
(2)

Число,
равное
,
называетсяскалярным
квадратом
вектора
.
Скалярный квадрат вектора равен квадрату
его длины.
Действительно,

Рассмотрим
ортонормированный базис
Очевидно,

.
(3)

Используя
свойства скалярного произведения и
учитывая (3), легко найти выражение
скалярного произведения через координаты
перемножаемых векторов в ортонормированном
базисе.

Теорема.
Если
,
то

(4)

Если
то из (4) найдем, что

Отсюда
следует формула косинуса угла между
векторами
и;

,
т.е.
.

Условие
перпендикулярности:
в том и только в том случае, если

Типовой
пример. Даны
точки: А(2;1;4),
В(0;-1;2),
С(4;3;-2).
Требуется: а) найти координаты вектора
;

б) найти угол
.

►а)
Найдем координаты вектора
:
из координат конца (точкаВ)
вычтем координаты начала (точка А):
.
Найдем координаты вектора:.
Найдем координаты вектора:

Найдем
координаты вектора
:

б) Найдем длины
векторов
ипо формуле.

Получаем:

Для
нахождения угла воспользуемся формулой

;

Ответ:

;.◄

Типовой
пример. Даны
точки A(–2; 1; 3), B(0;
–1; 2), C(3;
–2; 1).

Найти:
а) длину отрезка АВ; б) косинус угла B
в треугольнике АВС;
в)
;
г)
и направляющие косинусы.

►а)
;

б)
угол В в треугольнике АВС есть угол
между векторами
и.
Имеем,,
,
,

;

в)

,
,

отсюда
находим

;

г)
.

Направляющими
косинусами вектора
являются 2/3, –2/3, –1/3.

Типовой
пример.
Дано:
,,,.
Найти угол между векторамии.

►
Так как
или.

Таким
образом,
.
◄

Типовой
пример.
Найти длину вектора
,
если,,.

►

◄

3.
Векторное произведение и его свойства.
Векторным
произведением
упорядоченной пары неколлинеарных
векторовиназывается вектор,
удовлетворяющий следующим трём
требованиям:

1),
где
– угол между векторами
и;

2)

перпендикулярен каждому из векторови;

3)

образуют правую тройку.

Векторное
произведение принято также обозначать
.

Свойства
векторного произведения

1)
векторы

и
– коллинеарны;

2)

(антикоммутативность);

3)
,

(однородность);

4)
,

(дистрибутивность).

Выражение
векторного произведения через координаты
сомножителей

Найдем
векторные произведения базисных ортов
,
,
.
Результаты можно записать в табл. 1.

Таблица 1

Пользуясь
этой таблицей и свойствами векторного
произведения, легко найти формулу для
выражения векторного произведения
через декартовы координаты сомножителей.

Теорема.
Если
,
то

Типовой
пример. Вычислить
длину стороны АВ и площадь параллелограмма,
построенного на векторах
и,
если

А(3;2;1),
В(-1;0;2),
С(0;-1;1).

►Найдем
координаты вектора
:.
Длина стороныАВ
равна длине
вектора
:

Площадь
параллелограмма, построенного на
векторах
и, численно равна длине вектора.
Поскольку(-3;-3;0),
то

Т.е.
,
а его длина.
Значит:(кв. ед.).Ответ:
,(кв. ед.)◄

4. Смешанное
произведение векторов.
Смешанным
произведением
трех векторов ,
,

называется число, равное скалярному
произведению вектора
на векторное произведение векторов
и ,
т.е.
.

Геометрический
смысл смешанного произведения выражает
следующая теорема.

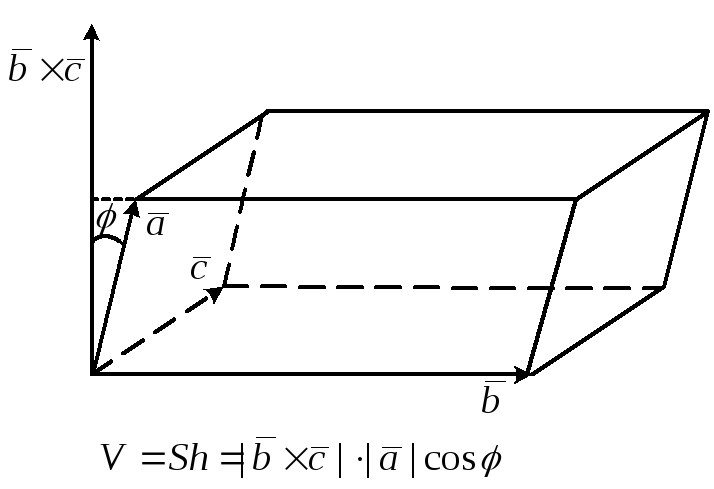
Теорема.
Смешанное
произведение
равно объему
параллелепипеда, построенного на
приведенных к общему началу векторах,
,
,
взятому со
знаком «плюс», если тройка векторов ,
,

правая, и со знаком «минус», если тройка
векторов ,
,

левая. Если же векторы ,
,

компланарны, то
.

В
краткой записи:

Свойства смешанного
произведения

1.

.
Данное равенствопозволяет обозначать смешанное
произведение векторов,
,

символом
,
не указывая при этом, какие именно два
вектора (первые или последние) перемножаются
векторно.

2.
Величина
векторного произведения не изменяется
при циклической перестановке сомножителей:

векторыкомпланарны.

4.
Смешанное
произведение линейно по каждому из
сомножителей. В частности,

Выражение
векторного произведения через координаты
сомножителей.

Теорема.
Если векторы
заданы своими координатами:,,,
то смешанное произведение
равняется
определителю, строки которого
соответственно равны координатам
перемножаемых векторов, т.е.

Действительно,.Тогда

Типовой
пример. Даны
точки A(4;
-1; 3), B(0;
1; 2), C(3;
-2; 5), D(1;
-1; 1). Найти: а) площадь треугольника АВС;
б) высоту
треугольника АВС, опущенную из вершины
А на сторону ВС; в) объём пирамиды АВСD.

►а)
Площадь
треугольника АВС равна половине площади
параллелограммаS,
построенного на векторах
и,
т.е..
Имеем,
,

;

б)

;

в)
Объём
пирамиды АВСD
равен
объёма параллелепипеда, построенного
на векторах.
Имеем,,;

.◄

Типовой пример.
Даны координаты
вершин пирамиды
.

►1)
Найти длину
ребра
.

2)
Найти угол между ребрами
и.

3)
Найти угол между ребром
и гранью.
Сначала найдем вектор нормали к граникак векторное произведение векторови.

=
(2-1;
1-0; 1-3) = (1; 1; -2),

Найдем
угол между вектором нормали и вектором
.

,
-4
– 4 = -8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
– .

4)
Найти площадь
грани

5)
Найти объем
пирамиды.

(ед³).◄

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

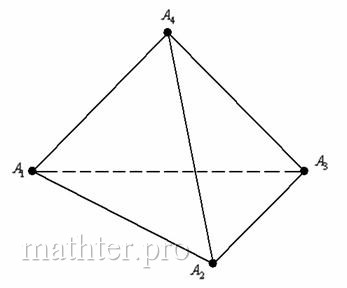
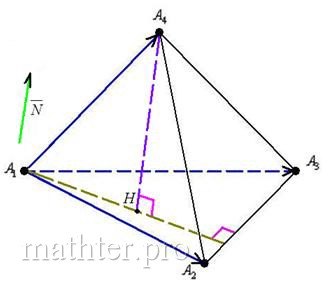
5.7. Задача с треугольной пирамидой

Концептуально эта задача напоминает задачу с треугольником на плоскости. Только вот треугольников у нас теперь

четыре, и образуют они треугольную пирамиду или тетраэдр:

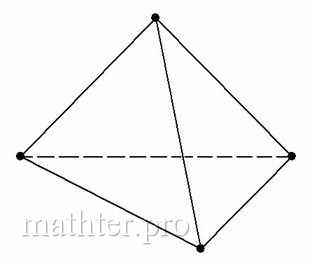
У треугольной пирамиды есть:

– четыре вершины;

– шесть рёбер (сторон);

– четыре грани.

Чем богаты, тем и рады.

Не буду перечислять геометрические свойства данной фигуры, известные из школьной программы, поскольку аналитическую геометрию интересует совсем

другое, а именно: уравнения рёбер, плоскостей, всевозможные длины, углы и некоторые другие вещи, которые вы увидите прямо сейчас. Типовая задача

формулируется так:

Задача 166

Треугольная пирамида задана координатами своих вершин, пусть это будут вершины . Требуется: … если повезёт, то только 3-4 пункта из перечисленных:

1) найти длину ребра ;

2) составить уравнения стороны ;

3) найти угол между рёбрами ;

4) найти площадь грани ;

5) найти угол между ребром и плоскостью ;

6) составить уравнение грани ;

7) составить уравнения высоты , опущенной из вершины на грань ;

вычислить длину высоты ;

9) найти основание высоты ;

10) вычислить объем пирамиды;

11) составить уравнения медианы грани ;

12) составить уравнение плоскости, проходящей через прямую и вершину ;

13) найти угол между плоскостями и

14) выполнить чертёж пирамиды в прямоугольной системе координат.

15) перекреститься левой пяткой.

Во-первых, разберёмся с обозначениями вершин. Самый распространённый вариант, когда они обозначены буквами :

Если бегло просмотреть пункты условия, то легко заметить, что

там часто встречается грань . Чаще всего требуется составить уравнение этой

«особенной» грани, а также найти её площадь. В качестве «особенной» вершины выступает точка , обычно из неё строится перпендикуляр к плоскости .

А всё это я сказал к тому, что в вашей задаче могут быть совершенно другие обозначения вершин. Например, . Здесь «особой» гранью, скорее всего, будет , а «особенной» точкой – вершина .

В этой связи очень важно выполнить схематический рисунок пирамиды, чтобы не запутаться в дальнейшем алгоритме решение. Да, более подготовленные

читатели могут представлять тетраэдр мысленно, но для «чайников» чертёж просто обязателен.

Итак, на предварительном этапе разбираемся с обозначениями вершин, анализируем условие, находим «особенную» плоскость и точку и

выполняем бесхитростный набросок на черновике.

С чего начать решение? Начать лучше всего с того, что загнать координаты вершин в Геометрический

калькулятор (см. приложения), который автоматически рассчитает наиболее популярные пункты. Ибо приятно заранее знать

правильные ответы

Но расписать-то всё нужно подробно. И поэтому оформление решения удобно начать с нахождения векторов. Почти всегда векторы

откладываются от первой вершины, в данном случае – от точки :
Решим эту элементарную задачу:

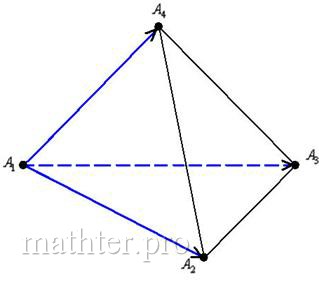
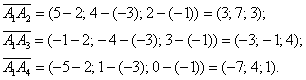
Чтобы комфортнее воспринимать информацию, координаты четырёх точек и трёх полученных вектора рекомендую переписать на отдельный листочек.

Это же сделайте, когда будете решать свою задачу – чтобы каждый раз не выискивать нужный вектор, нужную точку. Их удобно держать перед

глазами.

Понеслось:

1) Найдём длину ребра . Длина данного ребра равна длине вектора :

Я обычно округляю результаты до двух знаков после запятой, но в условии задачи может быть дополнительное указание проводить округления,

например, до 1 или 3 десятичных знаков.

Полагаю, в случае надобности никого не затруднит аналогичным образом найти длину ребра или . Как вариант, можно использовать

формулу расстояния между двумя точками: . Но зачем? У нас уже найдены

векторы.

2) Найдём уравнения ребра . Строго говоря, здесь следует

сказать «уравнения прямой, которая содержит ребро», но этим почти всегда пренебрегают. «По умолчанию» обычно подразумевается, что студент запишет канонические уравнения прямой.

Уравнения ребра составим по точке (можно взять ) и направляющему

вектору :

Для проверки подставляем координаты точек в полученное уравнение. Обе

должны «подойти».

3) Найдём угол между сторонами :

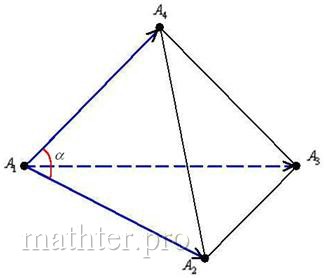
Перед вами обычный угол пространственного треугольника,

который рассчитывается как угол между векторами: . И снова при делах ~~задро~~ тривиальная формула:

– заметьте, что в ходе вычислений можно (и нужно) использовать ранее полученные результаты, в данном случае нам

уже известно, что (см. пункт 1).

С помощью обратной функции находим сам угол:

4) Найдём площадь грани :

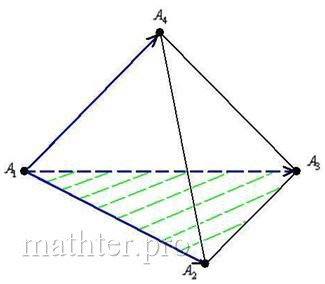
Площадь треугольника вычислим с помощью векторного произведения векторов, используя формулу:

Найдём векторное произведение:

и вычислим его длину:

…и вынести из-под корня ничего нельзя, поэтому он войдёт в ответ в

неизменном виде.

Таким образом, площадь грани :

Если получаются страшноватые числа, не обращайте внимания, обычная картина. Главное, не допустить ошибку в вычислениях.

5) Найдём угол между ребром и плоскостью , прошу прощения за неточность

последующих чертежей, я рисую от руки:

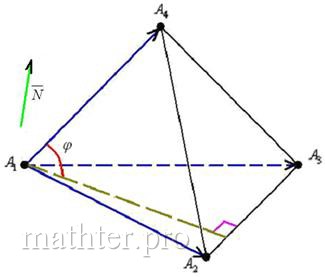
Это стандартная задача, рассмотренная в Задаче 162 (пункт

«д»). Используем формулу:

и с помощью арксинуса рассчитываем сам угол:

6) Составим уравнение грани . А точнее, «уравнение плоскости,

которая содержит грань». Первая мысль – использовать точки , но есть более выгодное решение. У нас уже найден

вектор нормали плоскости . Поэтому уравнение грани составим по точке (можно взять либо ) и вектору нормали :

Таким образом:

Для проверки можно подставить координаты точек в полученное уравнение, все три точки

должны «подойти».

7) Как составить уравнения высоты пирамиды? Звучит грозно, решается просто.

Уравнения высоты , опущенной из вершины на грань , составим по точке и направляющему

вектору :

– по умолчанию записываем канонические уравнения.

Вектор нормали в рассматриваемой задаче работает «на всю катушку», и как только вам предложили найти площадь грани, составить уравнение грани или

уравнения высоты – сразу «пробивайте» векторное произведение.

Длину высоты найдём как расстояние от точки до плоскости :

Результат громоздкий, поэтому позволим себе вольность не избавляться от иррациональности в знаменателе.

Теперь пунктик потруднее:

9) Найдём основание высоты – точку . Тема пересечения

прямой и плоскости подробно муссировалась в той же в Задаче 162 (пункт «б»). Повторим.

Перепишем уравнения высоты в параметрической форме:

Неизвестным координатам точки соответствует вполне конкретное значение

параметра :
, или: .

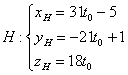
Основание высоты, понятно, лежит в плоскости. Подставим параметрические координаты точки в уравнение :

Кому-то покажется жестью, но на самом деле шифер Который шуршит.

Полученное значение параметра подставим в координаты нашей точки:

Сурово, но идеально точно. Я проверил.

10) Объём треугольной пирамиды в ангеме традиционно рассчитывается с помощью

смешанного произведения векторов:

Таким образом,

И тут уместно выполнить проверку, вычислив объем тетраэдра по школьной формуле , где – площадь грани, – длина высоты, опущенной к этой грани. Уместно ПОТОМУ, что мы знаем и площадь грани , и длину высоты :
, чему мы очень рады.

11) Составим уравнения медианы грани . Ничего сложного, обычная медиана обычного пространственного треугольника:
По сравнению с треугольником на

плоскости, добавится лишь дополнительная координата. Нам известны вершины , и по формулам координат середины отрезка находим адрес точки :

Уравнения медианы можно составить по двум точкам, но сначала (см. по ссылке, почему) лучше найти

направляющий вектор: . В качестве направляющего можно взять любой

коллинеарный вектор, и сейчас подходящий момент избавиться от дробей:

Уравнения медианы составим по точке и направляющему вектору :

Заметьте, что уравнения с эстетической точки зрения лучше составить по точке , так как координаты точки «эм» – дробные. Проверка обыденна, нужно подставить координаты точек в полученные уравнения.

12) Составим уравнение плоскости, проходящей через прямую и вершину :

Увы, мы не знаем «вкусный» вектор нормали, и поэтому уравнение

плоскости придётся добывать по точке и двум

неколлинеарным векторам.

В качестве точки обязательно выбираем «одинокую» точку, которая не принадлежит прямой, в данном случае – это вершина . Один из нужных векторов уже известен: , но, конечно же, удобнее выбрать друга-мажора . Ему в пару подходит вектор , но лучше .
Ибо координаты этого вектора будут целыми:

Уравнение плоскости составим по точке и двум неколлинеарным векторам :

Непременно проверяем, что координаты точек удовлетворяют

полученному уравнению.

13) Найдём угол между плоскостями и .

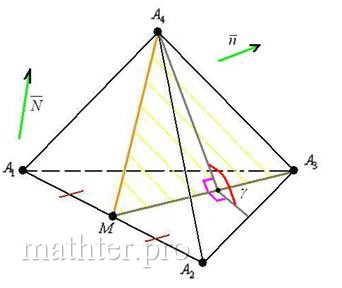
Это типовая задача.

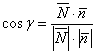
Обозначим искомый угол через и используем формулу: , где – вектор

нормали плоскости . Напоминаю, что вектор и его длина уже известны.

Осталось из уравнения снять вектор нормали: и аккуратно провести вычисления:

Возиться с такими корнями смысла нет, поэтому сразу находим угол:

От тупизны подальше за ответ таки лучше принять смежного соседа:

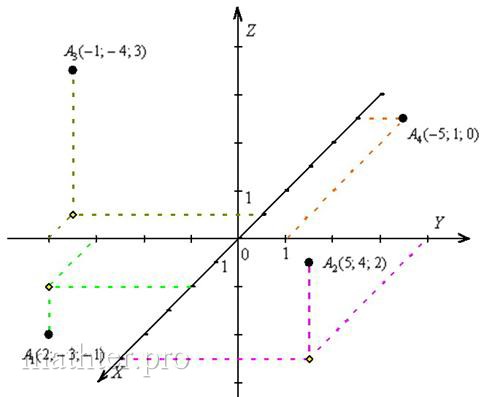
14) Выполним точный чертёж пирамиды прямоугольной системе координат. Да, конечно, существуют программы и онлайн сервисы для построения чертежей, но не

факт, что они под рукой, и не факт, что такой чертёж будет качественным. Поэтому я расскажу вам о ручном способе построения – в тетради с помощью

карандаша и линейки.

С чего начать?

Во-первых, нужно правильно изобразить декартову систему координат на клетчатой бумаге. Во-вторых, необходимо уметь строить точки в трёхмерном пространстве, о чём мы уже вспомнили, когда разбирали канонические уравнения прямой. И сейчас тема получает продолжение.

Построим точку . Для этого отмеряем 2 единицы в положительном направлении

оси и 3 единицы в отрицательном направлении оси . В плоскости прочерчиваем тонкие

пунктирные дорожки, которые параллельны соответствующим координатным осям. Пересечение этих дорожек отмечено ромбиком (слева

внизу):

Теперь, в соответствии с отрицательной «зетовой» координатой, отмеряем 1 единицу вниз и тоже проводим пунктирную дорожку. Здесь и будет находиться

наша точка , она расположена в нижнем полупространстве.

Для точки отмеряем 5 единиц «на себя» и 4 единицы вправо, строим параллельные

осям пунктирные дорожки и находим их точку пересечения. В соответствии с «зетовой» координатой, чертим пунктиром «подставку для точки» – 2 единицы

вверх. Данная точка расположена в верхнем полупространстве.

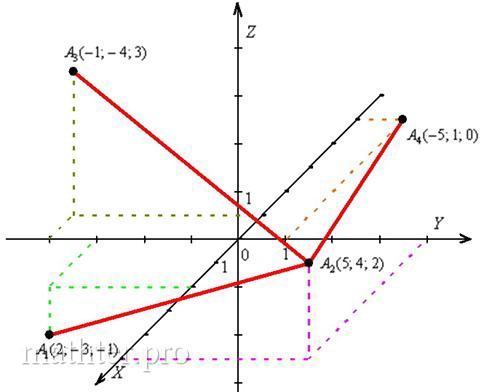
Аналогично строятся две другие точки. Заметьте, что вершина лежит в самой

плоскости .

Теперь нужно разобраться в удалённости точек, а в этом как раз и помогут пунктирные линии. Немного включаем пространственное воображение и

внимательно смотрим на ось . Очевидно, что самая близкая к нам вершина – , а самая удалённая – .

Строим рёбра. Если есть сомнения, то сначала тонко-тонко прочерчиваем все 6 сторон и начинаем разбираться, какие рёбра видимы, а какие нет. Лучше начать от самой близкой точки . Очевидно, что все

три «исходящих» ребра в поле нашего зрения:

Должен предостеречь, что так бывает далеко не всегда, одно ребро, например, может быть от нас скрыто. Не теряйте визуального восприятия

пространства!

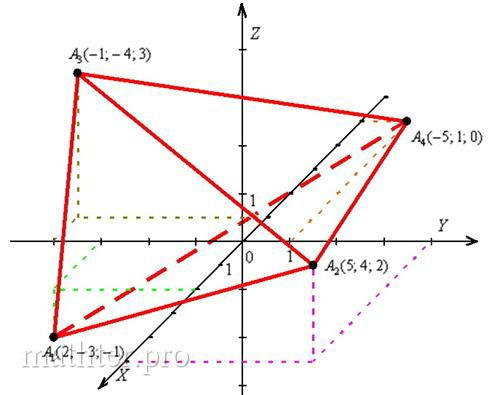
Какие ещё стороны в зоне видимости? ВиднЫ рёбра , а вот сторона спряталась за пирамидой. Обратите внимание, что она лежит в нижнем

полупространстве и проходит под осями :

Готово.

Следует отметить, что чертеж-«конфетка» получается далеко не всегда. Бывает, что фортуна разворачивается задом. Так, грань пирамиды может полностью

или частично закрывать всё остальное (слева).

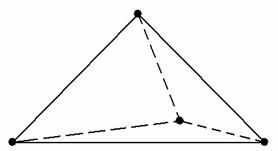
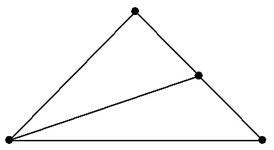
Но самое скверное, когда перекрываются рёбра (справа). Тут сразу три ребра выстроились на одной прямой (правая верхняя прямая). В

подобной ситуации можно жирно прочертить накладывающиеся стороны разными цветами и ниже чертежа записать дополнительные комментарии о расположении

пирамиды. А можно поступить творчески – поменять оси местами (например, и ).

Существуют и более мелкие неприятности, например, одна из сторон пирамиды может наложить на координатную ось (а то и вовсе расположиться за ней).
Увы, перечисленные случаи – не редкость на практике.

В конце решения следует выполнить Пункт 15, после чего желательно записать ответ, где по пунктам перечислить

полученные результаты.

6.1. Поверхности второго порядка

5.6.7. Добро пожаловать в «реальные боевые условия»!

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник

Любой вектор в декартовой системе координат может быть представлен в виде

Где координаты вектора Орты координатных осей.

Вектор с началом в точке и концом в точке Имеет вид:

то есть .

Длина отрезка называется Длиной (модулем) вектора, обозначается = и вычисляется по формуле

Сумма векторов и определяется формулой

Произведение вектора На число определяется формулой

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними, т. е.

Скалярное произведение векторов и вычисляется по формуле:

Векторным произведением векторов и называется вектор, обозначаемый и удовлетворяющий следующим условиям:

1) длина вектора равна площади параллелограмма, построенного на векторах и , т. е. ;

2) вектор перпендикулярен векторам и ;

3) векторы образуют правую тройку, то есть они ориентированы по отношению друг к другу соответственно как орты .

Модуль векторного произведения векторов и численно равен площади параллелограмма, построенного на этих векторах:

Векторное произведение векторов и вычисляется по формуле:

Смешанным произведением векторов называется скалярное произведение вектора на вектор , то есть .

Модуль смешанного произведения векторов численно равен объему параллелепипеда, построенного на этих векторах:

Пусть Тогда

Уравнение любой плоскости может быть записано в виде:

где .

Вектор , перпендикулярный плоскости, называется Нормальным Вектором плоскости.

Уравнение плоскости, проходящей через точку и перпендикулярной вектору , имеет вид

Угол между плоскостями и определяется следующим образом:

Расстояние от точки До плоскости, определяемой уравнением , находится по формуле

Прямая В пространстве может быть задана уравнениями двух плоскостей

Пересекающихся по этой прямой, или Каноническими уравнениями прямой

Которые определяют прямую, проходящую через точку и параллельную вектору . Вектор называется Направляющим вектором прямой.

Уравнения прямой, проходящей через две точки и , имеют вид:

Угол между Двумя прямыми и определяется следующим образом:

Угол между прямой и плоскостью определяется следующим образом:

Если Точка Делит отрезок АВ, где ,, в Отношении, то координаты точки М определяются по формулам:

Задание 1. Даны координаты вершин пирамиды : , . Найти: 1) длину ребра ; 2) угол между ребрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объем пирамиды; 6) уравнения прямой ; 7) уравнение плоскости ; уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Решение. 1) Для определения длины ребра найдем координаты вектора : . Тогда длина ребра будет равна длине вектора :

2) Найдем угол между ребрами и . Для этого, как и раньше, найдем координаты вектора , определяющего ребро . Получим и .

Тогда угол между ребрами и можно найти из определения скалярного произведения двух векторов:

Следовательно, .

3) Чтобы найти угол между ребром и гранью , определим нормальный вектор Плоскости . Из определения векторного произведения двух векторов имеем:

Т. е. и . Тогда , .

Так как нормальный вектор перпендикулярен плоскости , то угол между ребром и гранью определяется как .

4) Площадь грани можем найти по формуле . Следовательно, Кв. ед.

5) Объем пирамиды, построенной на векторах, равен 1/6 объема параллелепипеда, построенного на этих же векторах. Для определения объема параллелепипеда воспользуемся свойством смешанного произведения векторов. В результате имеем:

Таким образом, куб. ед.