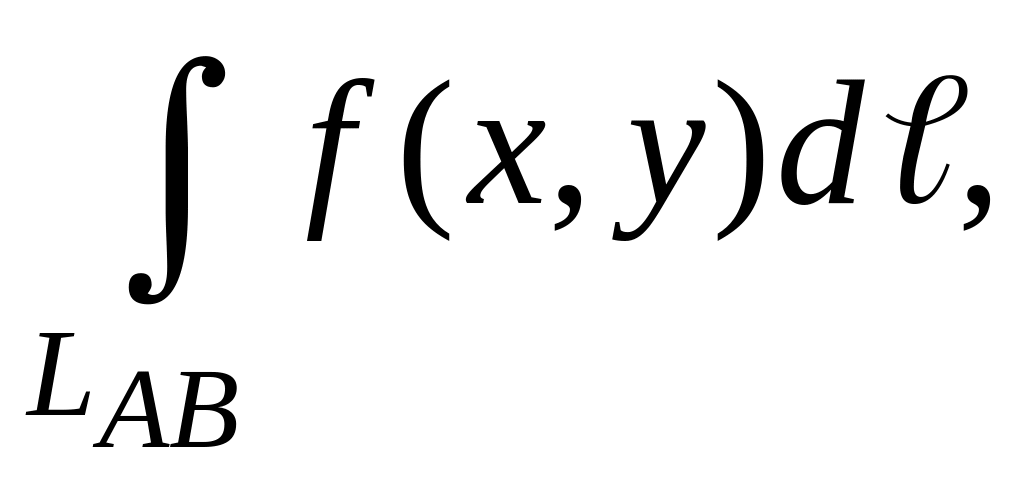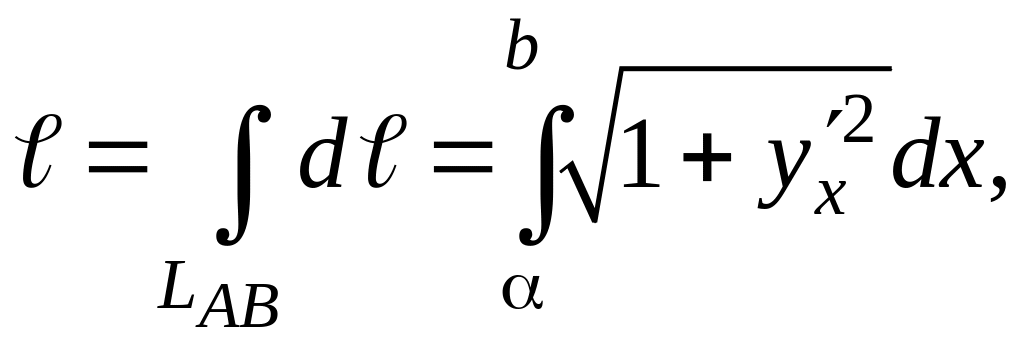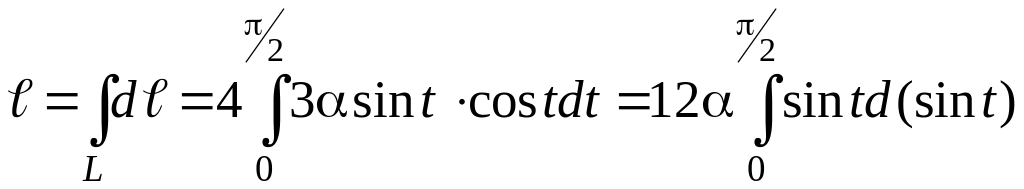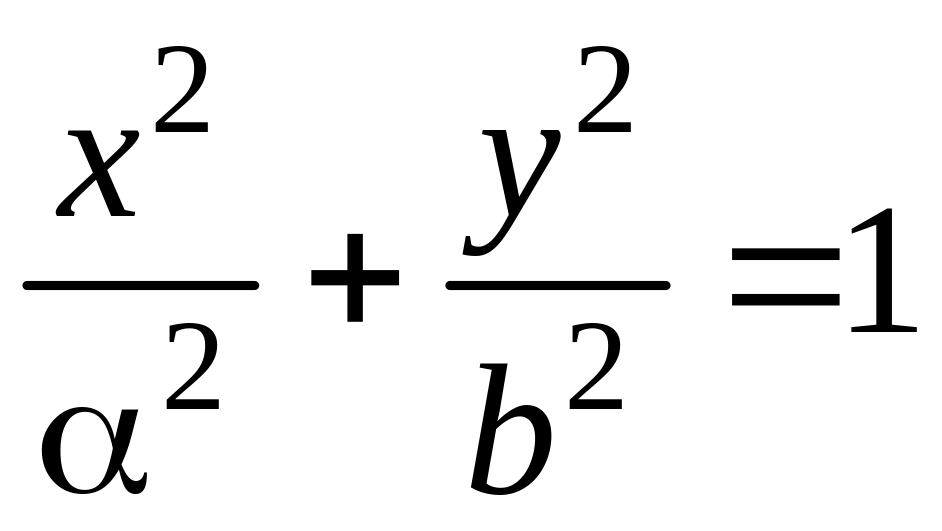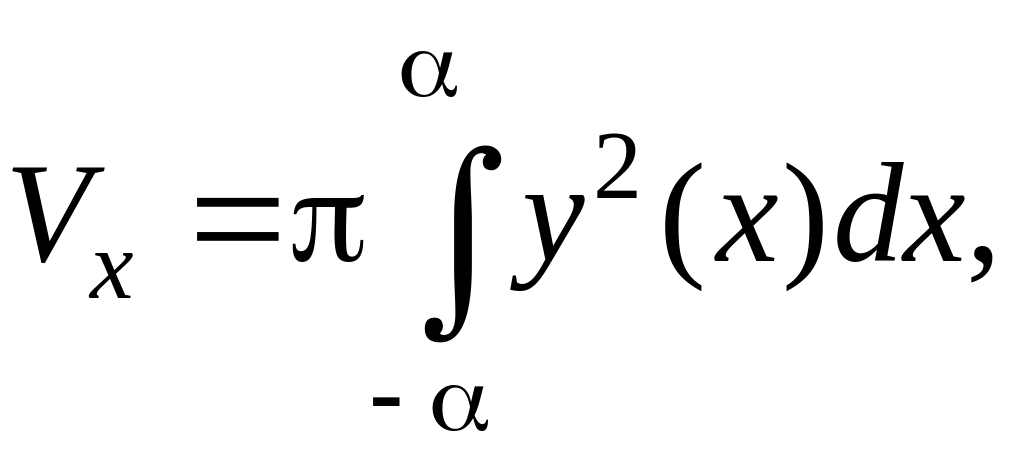Как найти длину смещенной линии - Исправление недочетов и поиск решений вместе с Examum.ru

Как сместить линию?

Затем выполните следующие действия:

Выберите инструмент «Смещение» ( ) или нажмите клавишу F.
Щелкните один из выбранных сегментов линии или грань, которую вы хотите сместить.
Переместите курсор, чтобы определить размер смещения. …
Переместите курсор, чтобы определить размер смещения. …
Нажмите, чтобы завершить смещение.

Тип O или смещение в командной строке и нажмите Enter. Укажите расстояние смещения. Например, 1. Выберите объект для смещения.

: режущий инструмент, режущая кромка которого не находится на одной линии с хвостовиком.

Можно ли сместить линию в Arcmap?

Наблюдения и советы этой статьи мы подготовили на основании опыта команды Линия смещения окно позволяет являетесь добавить COGO линий по обе стороны от указанной центральной линии. Укажите параметры, такие как начальное расстояние вдоль линия, сторону и длину, чтобы создать новый линия. на панели инструментов редактора. Щелкните линия функция или функции, для которых являетесь хочу создать линия смещения.

Что вы имеете в виду под размером и смещением?

Приведенное значение смещения представляет расстояние от указанных размерных точек на виде до начала выносных линий. … Вы можете установить смещение выносных линий размера от размерной линии. Приведенное значение смещения представляет собой расстояние от размерной линии до конца выносных линий.

Почему я не могу сместить линию в AutoCAD?

Когда мы перемещаемся по команде OFFSET, мы получаем «Невозможно сместить этот объект». сообщение в командной строке. Если наша полилиния была создана путем ввода данных съемки, у нас могут быть некоторые перекрывающиеся сегменты, сегменты нулевой длины или другая нежелательная геометрия.. Эти элементы могут привести к невозможности смещения объекта.

Что можно создать из команды offset?

Создает концентрические окружности, параллельные линии и параллельные кривые. Вы можете сместить объект на указанное расстояние или через точку. После смещения объектов их можно обрезать и удлинить, что является эффективным методом создания чертежей, содержащих множество параллельных линий и кривых.

Как добавить смещение к изображению?

Как использовать смещение

ШАГ 1: ИМПОРТ ИЗОБРАЖЕНИЯ В ПРОСТРАНСТВО ДИЗАЙНА. Начните с вставки изображения или текста на холст пространства дизайна. …
ШАГ 2: ВЫБЕРИТЕ СМЕЩЕНИЕ. …
ВЫБЕРИТЕ СТИЛЬ УГЛА. …
ШАГ 4: ВЫБЕРИТЕ ИЛИ ОТМЕНИТЕ ВЫБОР СВАРКИ. …
ВЫБЕРИТЕ ПРИМЕНИТЬ. …
ИЗМЕНИТЬ ЦВЕТ И КОНТУР. …
(ДОПОЛНИТЕЛЬНО) ВЫРАВНИТЕ ДЛЯ ПЕЧАТИ, ЗАТЕМ РАЗРЕЗАЙТЕ.

Инструмент «Смещение» в SketchUp дает нам возможность создать новый контур из уже существующей формы, которая у нас есть. Этот инструмент очень поможет нам, когда мы хотим нарисовать план, так как мы можем задать Смещение определенного размера, чтобы нарисовать ширину внешних стен здания всего одним движением.

Сколько существует типов смещения?

РЕКЛАМА: Смещения классифицируются по направлению и длине, по направлению Два типа т. е. перпендикулярные смещения и наклонные смещения в зависимости от длины, т. е. короткие смещения и длинные смещения.

Как сместить точки в ArcGIS?

На вкладке «Позиция» разверните узел Размещениеи выберите Лучшее положение в раскрывающемся списке. В разделе Размещение укажите Предпочтительное смещение, Максимальное смещение и Измерить смещение от. Дополнительную информацию см. в ArcGIS Pro: метки точки смещения.

Как вы смещаете линии в ArcGIS pro?

Создание объектов вдоль линии со смещением

На вкладке «Правка» в группе «Возможности» нажмите «Изменить» . …
Разверните Конструкцию и щелкните Смещение . …
Установите флажок Предварительный просмотр, чтобы отобразить предварительный просмотр вспомогательной линии.
Чтобы нарисовать вспомогательную линию с двумя точками, выполните следующие действия: …
Чтобы трассировать вспомогательную линию с двумя точками, выполните следующие действия:

Как нарисовать параллельную линию в Arcmap?

Чтобы создать новый сегмент, параллельный другому сегменту, нажмите «Ограничение параллельности» на панели инструментов «Построение элементов» и щелкните сегмент. При перемещении указателя может измениться длина сегмента, но не угол. Например, вы можете использовать эту команду для создания газопровода параллельно улице.

Источник

Длину
плоских кривых, заключенных между двумя
точками А
и В,
можно найти с помощью криволинейного
интеграла

если положить f(x,y)
≡ 1. В этом случае криволинейный интеграл,
также как и двойной, будет равен размерам
области интегрирования, т.е. длине части
линии L_AB.

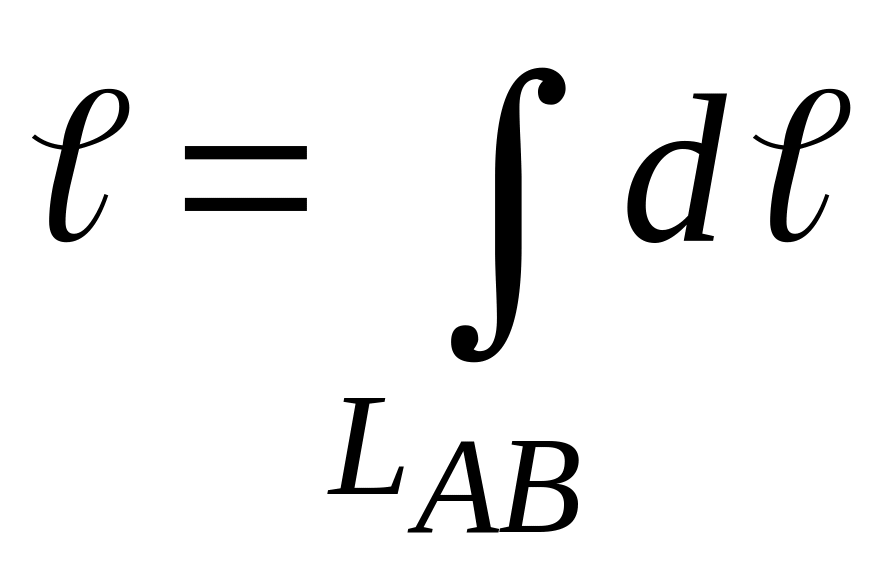
Меру
элементарной части (дифференциал длины)
— dℓ
выражают через уравнение данной линии
L_AB
и переходят к линейному интегралу. Если
кривая L_AB
задана в декартовой системе координат
непрерывной и дифференцируемой функцией
y
= y(x),
то вычисление ее длины сводят к вычислению
линейного интеграла вида:

где

Пределы
в линейном интеграле α
и b
– являются проекциями на ось Oх
точек линии А
и В
соответственно.

Длину
дуги АВ
кривой, заданной параметрическими
уравнениями x
= x(t);
y
= y(t),
находят по формуле

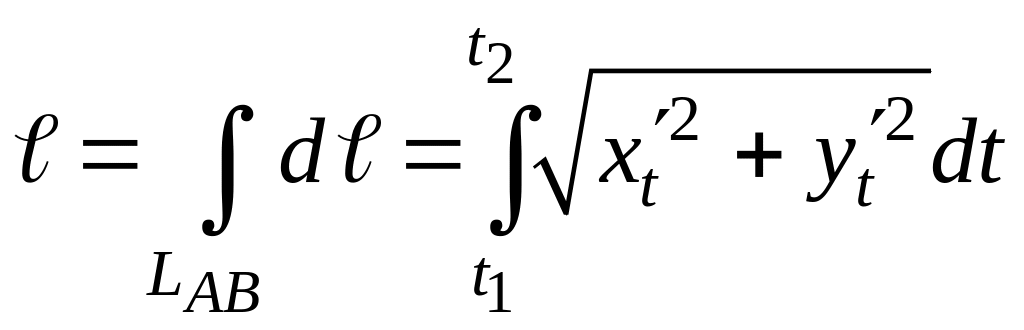
где
t₁
и t₂
значения параметра t
в точках А
и В.

И
наконец, длина линии L_AB,
уравнение которой r
= r(φ)
задано в полярной системе координат,
равна линейному интегралу

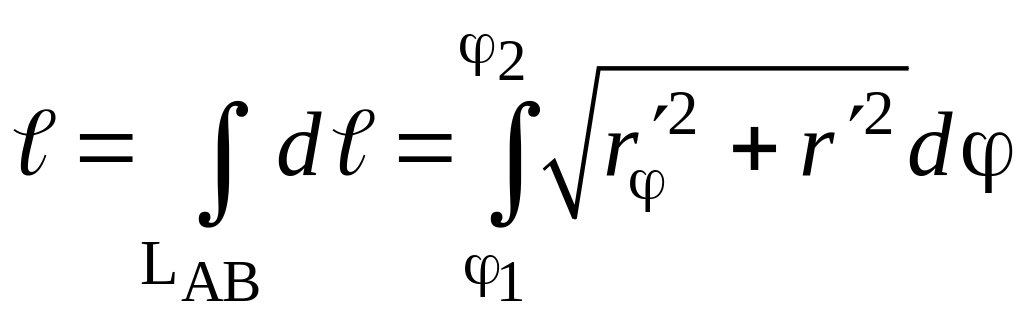
где
φ₁
и φ₂
полярные углы точек А
и В.

Пример
5. Найти длину
полукубической параболы y²
= x³
от точки А(0,0)
до точки В(4;8).

Решение.
Длина отрезка полукубической параболы
между точками А
и В
равна криволинейному интегралу

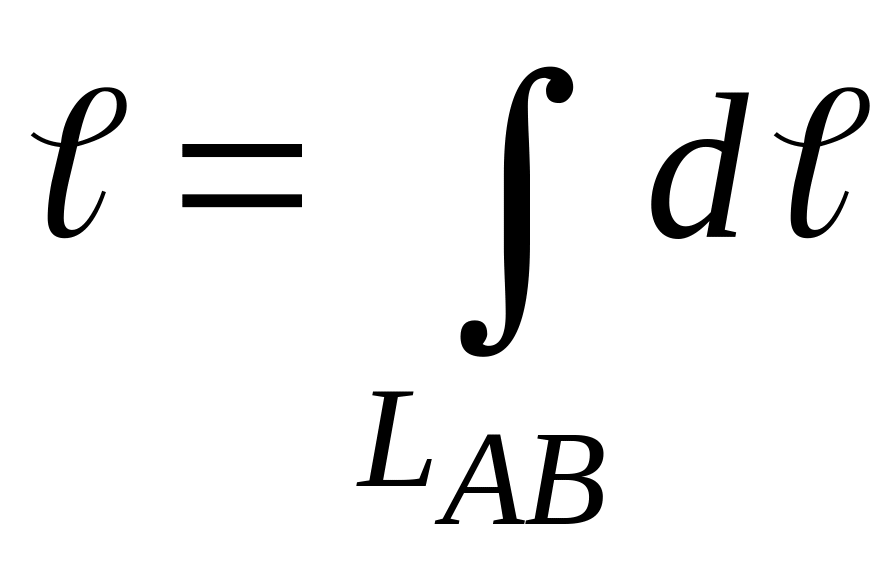
Дифференциал
длины кривой в
декартовой системе координат
выражают через ее уравнение y
= y(x)
по формуле

Найдем
его для данной линии

Переход
от криволинейного интеграла к линейному
и вычисление последнего дает искомую
длину:

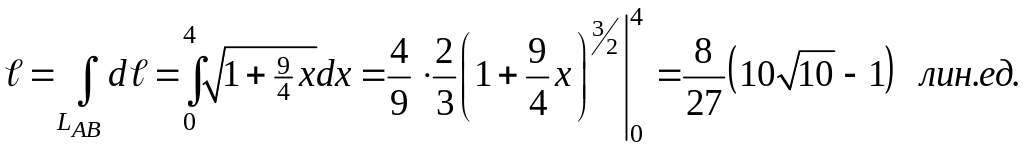
Пример
6. Найти длину
астроиды, заданную
параметрическими уравнениями

Решение.

Длину астроиды
также найдем с помощью криволинейного
интеграла

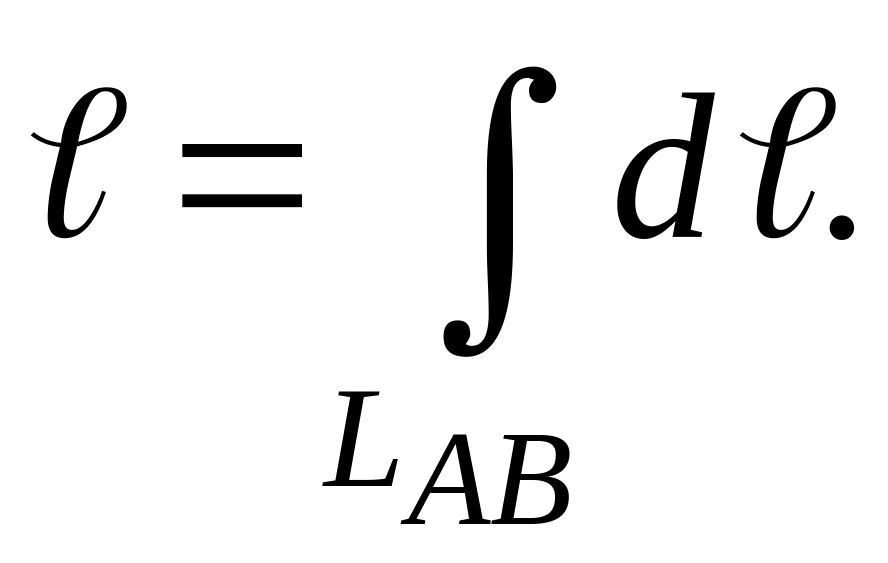
Дифференциал
длины кривой, заданной параметрически,
выражают через ее уравнение по формуле

Найдем его для
астроиды

Подставляя
найденное выражение для dℓ
в криволинейный интеграл и переходя к
линейному, получим:

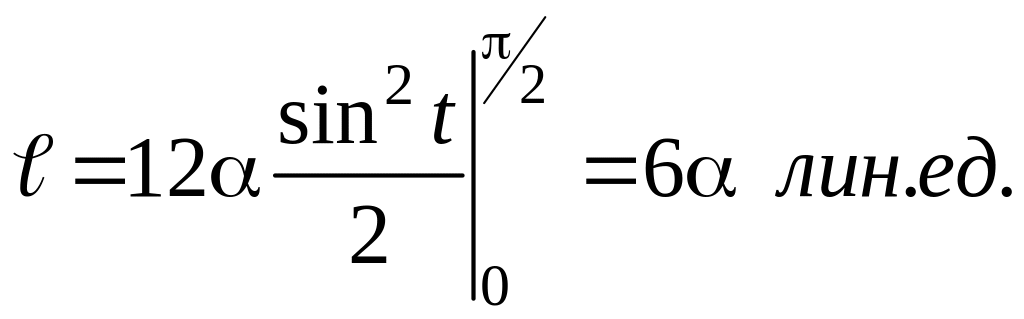
3.11.3.Вычисление объемов тел

Объем
тел, в зависимости от их формы и условий
задачи, можно находить различными
способами.В частом случае, когда известна
площадь поперечных сечений тела, его
объем вычисляют с помощью линейного
интеграла
по формуле:

где
S(x)
– площадь сечения тела плоскостью,
перпендикулярной оси Ox,
α
и b
– проекции его крайних точек на ту же
ось.

Исходя
из этой формулы, находят объем тел
вращения.

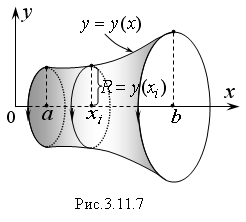
П
усть
криволинейная трапеция, ограниченная
сверху графиком непрерывной функции y
= y(x)
и прямыми x
= α,

x
= b,
вращается вокруг оси Oх
(Рис. 3.11.7).

В
результате ее вращения образуется тело.
Его плоскими сечениями, перпендикулярными
оси Oх,
являются круги с различными радиусами

R
= y(x),
площадь которых равна:

Следовательно,
объем полученного тела можно найти по
формуле

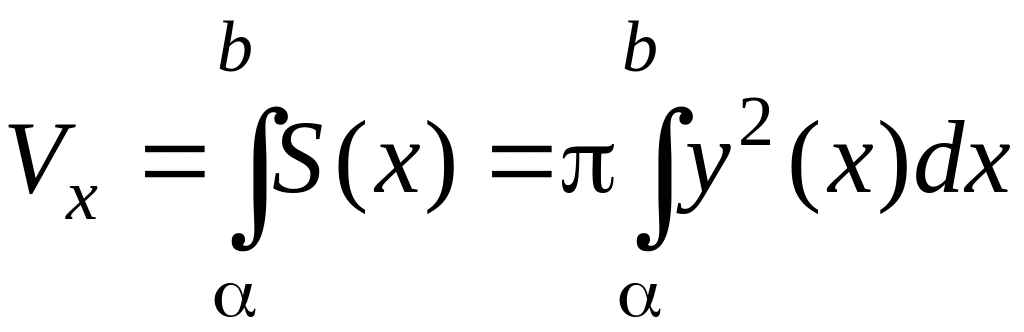
П
ри
вращении линии, ограничивающей
криволинейную трапецию, вокруг оси Oy
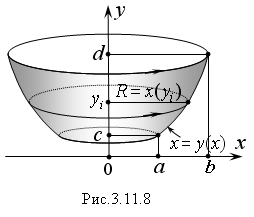
(Рис. 3.11.8) объем полученного тела равен:

где
x(y)
– уравнение вращающейся линии решенное
относительно переменной x.

Пример
7. Найти объем
тела, полученного при вращении эллипса
относительно осей Ox
и Oy.

Р
ешение.
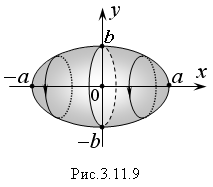
График эллипса

изображен на рисунке 3.11.9.

Координаты
его крайних точек по оси Oх:

x₁
= –α,
x₂
= α,
по оси Oy:
y₁
= –b,
y₂
= b.

Объем
тела, образованного вращением эллипса
относительно оси Oх,
найдем по формуле:

где

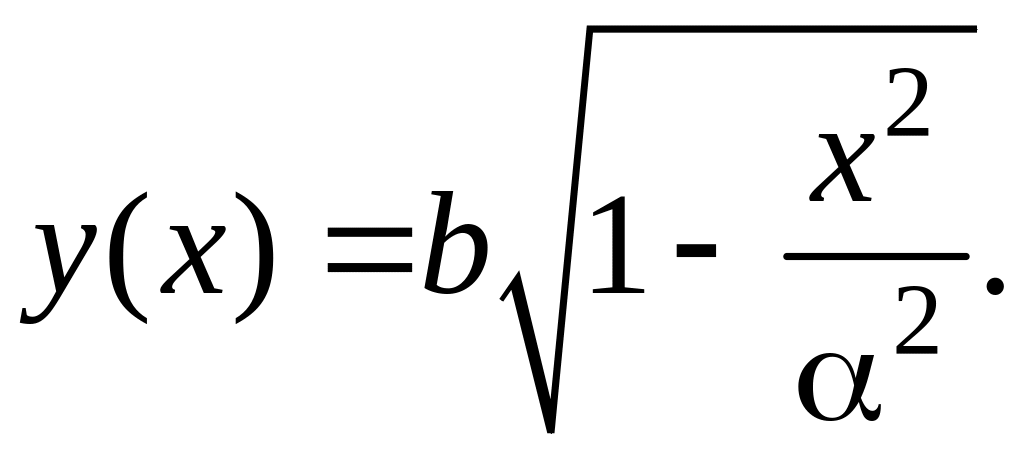
С учетом симметрии

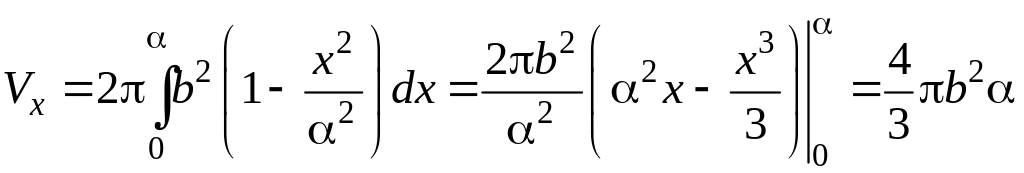
Аналогично,
вычислим объем Vy

где

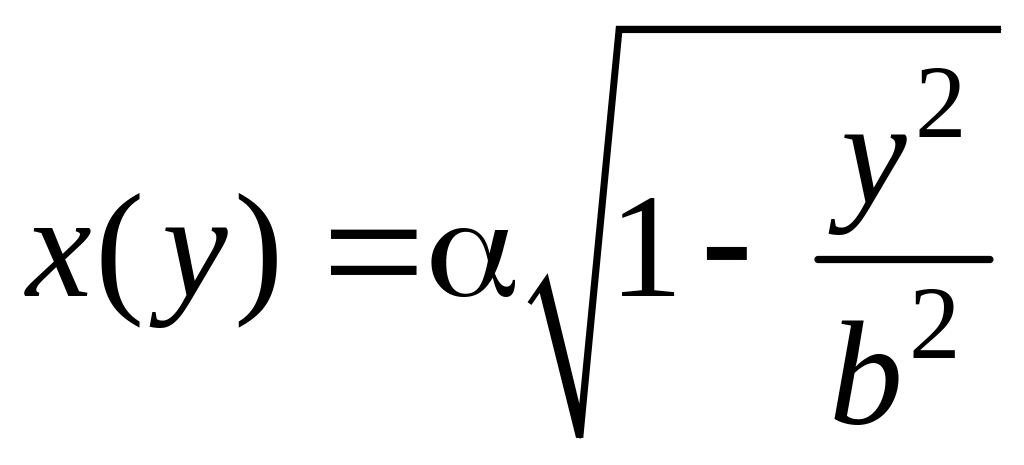
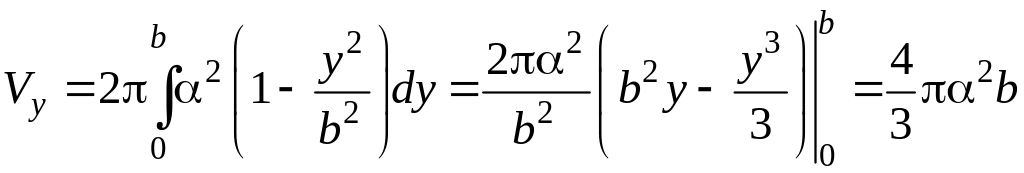
Если
α
= b,
то тела вращения относительно осей Oх
и Oy
становятся шаром, объем которого равен

.

Р
ассмотрим
теперь общий случай вычисления объемов
тел с помощью кратныx
интегралов.

Пусть
тело произвольной формы ограничено
двумя поверхностями, уравнения которых
известны:

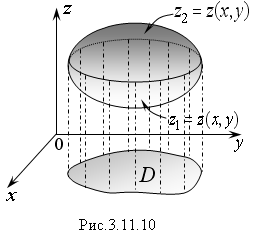
Проекцией данного тела на плоскость
xOy
является область D
(Рис. 3.11.10). Двойной интеграл по области
D
геометрически равен объему цилиндра,
построенного на этой области и
ограниченного сверху графиком
подынтегральной функции. Поэтому объем
тела, изображенного на рисунке 3.11.10,
можно представить как разность объемов
двух цилиндрических тел, или как разность
двух двойных интегралов:

В
самом общем случае объем тел произвольной
формы находят с помощью тройного
интеграла,
в котором подынтегральная функция равна
единице

Легко
заметить, что предыдущая формула является
следствием последней, в самом деле:

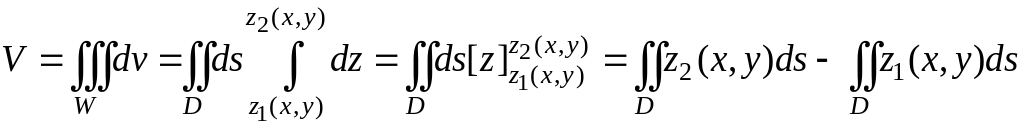
Пример
8. Найти
объем, ограниченный поверхностями:

z
= 0, z
+ x
= 6

Р
ешение.
Тело ограничено двумя цилиндрическими
поверхностями

с образующими, параллельными оси Oz,
и двумя плоскостями z
= 0, z
= 6 – x.
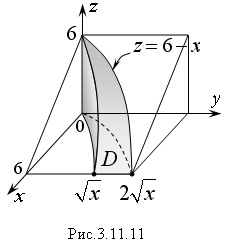
Искомый объем равен объему цилиндрического
тела, построенного на области D
и ограниченного сверху плоскостью z
= 6 – x
(Рис. 3.11.11). Найдем его с помощью двойного
интеграла

Переменная
x
внутри области D
изменяется от 0 до 6, а переменная y
от ее значений на линии

до значений на линии

.
Перейдем к двукратному интегрированию:

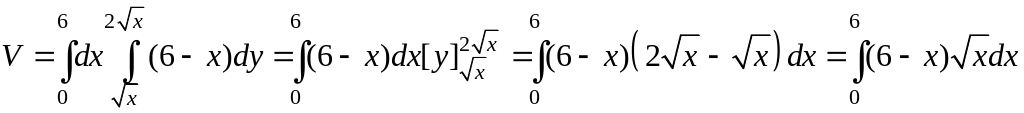
Вычисляя последний
интеграл, получим

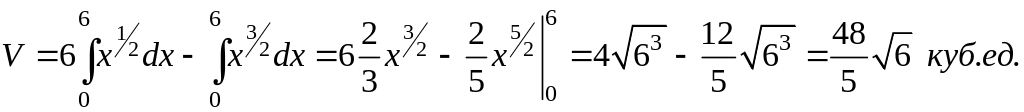
Для сравнения
найдем этот же объем с помощью тройного
интеграла

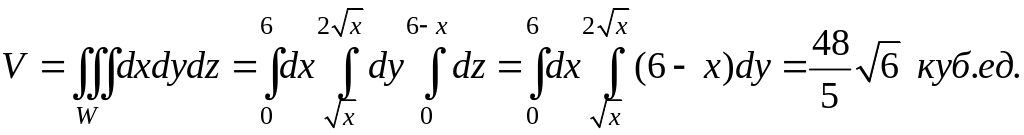
После
подстановки пределов для переменной z
мы приходим к такому же двойному
интегралу.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Математика провисающих проводов и цепей в играх

Время на прочтение
5 мин

Количество просмотров 12K

Во многих современных играх присутствуют провода, кабели и цепи. В этой статье мы рассмотрим математические модели, от которых зависит их форма, также называемая catenary («цепная линия»).

Введение в цепные линии

Из множества изученных и описанных математических объектов один очень дорог многим разработчикам игр. И только некоторые из них знают его истинное название: цепная линия.

Цепная линия — это фигура, к которой естественным образом сводится подвешенная за края верёвка или цепь. Неслучайно само название catenary происходит от латинского catenaria, что и означает «цепь».

В современных играх появляется всё больше заброшенных предприятий и разрушенных окружений. И во многих из них встречается довольно много свисающих проводов. Например, их можно увидеть в комнате GLaDOS из «Portal» или в «Half-Life: Alyx».

Так как цепные линии окружают нас повсюду, неудивительно, что мы с детства привыкли к их форме. А ещё это означает, что мы очень легко замечаем, когда что-то свисает неправильно. Подобно сложности движения кожи или физики ткани, неправильное свисание цепных линий само по себе создаёт эффект «зловещей долины».

Тем не менее, в очень многих играх цепные линии реализуют неправильно! Однако причина этого неудивительна. Хоть их так легко создавать в реальной жизни, их математическое описание — настоящий кошмар. За исключением нескольких особых случаев, «простых» уравнений для генерации цепной линии не существует; по крайней мере, не в том виде, который нужен для украшения уровня.

Один из стандартных способов создания физически обоснованных цепных линий без затрат — использование твёрдых тел (rigid bodies) и шарниров (hinge joints) при создании цепей и верёвок. Это имеет и дополнительное преимущество — они реагируют на действия игрока, однако ценой затратных вычислений. Большинство свисающих проводов и кабелей является частью фона, и использовать физику для их создания было бы слишком затратно. Следовательно, очень важно иметь возможность создавать статические цепные линии без вычислений в реальном времени.

Кроме того, отрисовка цепных линий имеет ещё одно преимущество. Допустим, что нам нужно создать для игры настоящий, управляемый физикой свисающий провод. Как располагать сегменты провода при его создании в игре? Многие разработчики бы просто разместили их вдоль линии, позволив физическому движку самому выбрать равновесное состояние. Отрисовка цепных линий позволяет инициализировать физически верные провода и кабели уже в их состоянии равновесия, без необходимости ждать, пока они сами остановятся в нужном положении.

Стоит заметить, что в Unity нет встроенных инструментов для кабелей и цепей, а в Unreal Engine существует Cable Component, решающий как раз эту задачу при помощи техники Verlet Integration (которая станет темой моих будущих статей). А на случай, если вам нравятся шейдеры, Росс Бёрдсэлл недавно создал гениальное решение для симуляции спиральных шнуров в Unreal Engine 4.

Формальное определение

Если мы хотим получить физически корректные цепные линии, то, наверно, лучше начать с начала. Простейшая цепная линия задаётся однозначно определённым уравнением с использованием

$cosh$ — гиперболического косинуса:

$begin{equation*} y=a cosh{left(frac{x}{a}right)}end{equation*} (1)$

Уравнение цепной линии имеет параметр

$a$ , меняющий общую «ширину» кривой. Однако все кривые цепных линий похожи, потому что все они являются версиями друг друга с разным масштабом. Ниже показано изменение кривой как функции от

$a$ (в оригинале статьи анимация интерактивна):

Что такое гиперболический косинус?

Многие из вас знакомы с более «традиционной» функцией косинуса. Синус и косинус задаются на окружности, а их гиперболические аналоги — на гиперболе (см. анимацию ниже).

Их естественной областью использования является изучение гиперболической геометрии. Также они часто оказываются решением множества дифференциальных уравнений. На самом деле,

$sinh$ и

$cosh$ играют важную роль в решении следующего дифференциального уравнения:

$f^{primeprime}=f$

а именно:

Также они сильно связаны с

${rm e}^{x}$ :

$begin{split}sinh{x} & = frac{{rm e}^{x}-{rm e}^{-x}}{2} \cosh{x} & = frac{{rm e}^{x}+{rm e}^{-x}}{2} \end{split}$

Покажите, как выводится уравнение!

Вывод уравнения цепной линии — сложная задача, требующая довольно продвинутого математического анализа. Если вам любопытно, на Math24 есть очень подробная статья Equation of Catenary, пошагово демонстрирующая его вывод.

Вывод уравнения начинается с допущения о том, что для каждого небольшого сегмента цепи гравитационные силы находятся в идеальном балансе с силой натяжения от соседних сегментов. Это приводит к созданию системы уравнений, при решении которой мы получаем (1):

$y=a cosh{left(frac{x}{a}right)}$

Этот вывод также даёт нам некое понимание того, что же на самом деле означает параметр

$a$ :

$a = frac{T_0}{ρ g A}$

где:

Как используют цепные линии?

Кроме использования для воссоздания висящих цепей, цепные линии особенно полезны во множестве других областей применения. Их форма образуется благодаря тщательному балансу между внутренним натяжением цепи и силой гравитации. Такое равновесие означает, что вес самой цепи равномерно распределён вдоль всей длины. Благодаря этому перевёрнутые цепные линии становятся идеальной формой для свободно стоящих арок постоянной толщины.

Доктор Том Кроуфорд рассказывал об этом в недавнем видео Numberphile, объясняя, как внутренняя структура купола собора Святого Павла в Лондоне поддерживается перевёрнутой трёхмерной цепной линией.

Цепные линии обладают и ещё одним любопытным свойством. Они являются формой, позволяющей квадратам перемещаться без колебаний их центров (см. анимацию ниже).

Параметризация цепной линии

Если мы хотим научиться рисовать физически точные цепные линии, то (1) может быть не лучшим способом для этого. Причина проста: кроме изменения

$a$ у нас практически нет никакого контроля над тем, где и как их можно разместить.

Более «настраиваемым» уравнением является (2), позволяющее перемещать кривую горизонтально и вертикально при помощи двух дополнительных параметров

$p$ и

$q$ :

$begin{equation*} y=a cosh{left(frac{x-p}{a}right)}+qend{equation*} (2)$

Однако в идеале нам бы подошло уравнение цепной линии, проходящей через две точки закрепления

$P_1$ и

$P_2$ :

$begin{split}P_1 & = left(x_1, y_1right) \P_2 & = left(x_2, y_2right)end{split}$

Параметр

$p$ позволяет перемещать вершину цепной линии; когда

$p=0$ , вершина находится на оси Y. Мы можем сдвигать цепную линию так, чтобы вершина находилась ровно между

$P_1$ и

$P_2$ :

$p=frac{x_1+x_2}{2}$

На самом деле, это идеально, если и

$P_1$ , и

$P_2$ находятся на одном уровне (т.е. когда

). Но если это не так, то получившаяся цепная линия будет физически неверной. Кроме того, это почти не позволяет нам управлять степенью провисания цепной линии. Поэтому нам нужно подойти к задаче по-другому: нам нужен более «художественный» способ управления линией.

Решение задачи цепной линии

В этом разделе мы покажем уравнения физически правильной цепной линии, представляющей верёвку, закреплённую в двух точках пространства,

$P_1$ и

$P_2$ , с заданной длиной

$l$ . Математический вывод уравнения довольно запутан, поэтому чтобы не мучить вас, я просто покажу результат решения.

Для начала зададим два вспомогательных параметра,

$h$ и

$v$ , указывающих горизонтальное и вертикальное расстояние между двумя точками.

$begin{equation*}begin{split}h & = x_2 - x_1 \v & = y_2 - y_1 \end{split}end{equation*} (3)$

При выводе уравнения мы предполагаем, что

; если это не так, то можно просто поменять местами две точки. Также нам нужно задать условие, что

$l$ больше расстояния между двумя точками. Это кажется справедливым, ведь длина цепной линии должна быть не меньше расстояния между точек закрепления.

Мы получаем следующие значения для

$p$ и

$q$ :

$begin{equation*} p=frac{x_1+x_2-a ln{left(frac{l+v}{l-v}right)}}{2}end{equation*} (4)$

$begin{equation*} q=frac{y_1+y_2-l coth{left(frac{h}{2a}right)} }{2}end{equation*} (5)$

где

$coth$ — гиперболический котангенс:

$coth{x}=frac{cosh{x}}{sinh{x}}$

На показанной ниже анимации (в оригинале статьи она интерактивна) перемещается вторая точка закрепления (

$P_2$ ) и меняется длина цепи (

$l$ ), при этом изменяется форма линии.

Находим a

В предыдущем разделе нам не удалось представить уравнение первого параметра цепной линии:

$a$ . Так получилось, потому что в этом случае нет лаконичного решения, способного вычислить его точное значение. На самом деле, при любых попытках вывода

$a$ мы придём к следующему трансцендентному уравнению:

$begin{equation*} sqrt{l^2-v^2}=2 a sinh{left(frac{h}{2 a}right)}end{equation*} (6)$

Иными словами, мы не можем преобразовать это уравнение в более простой вид

$a=...$ так, чтобы

$a$ не находилась и в правой части уравнения. Иногда трансцендентные уравнения можно переписать в таком виде, но часто это требует бесконечного количества операций (например, использования рядов или интеграла).

Когда такое происходит, то это значит, что нам нужен другой способ вычисления значения

$a$ . Если не получается решить задачу аналитически, то приходится использовать численные решения. То есть нам нужно использовать алгоритм для поиска приблизительного решения. Об этом мы поговорим в следующей статье.

Источник