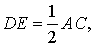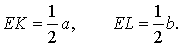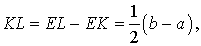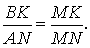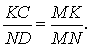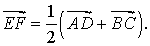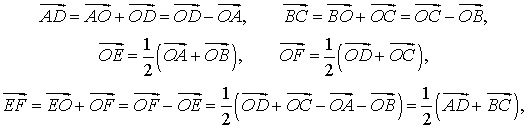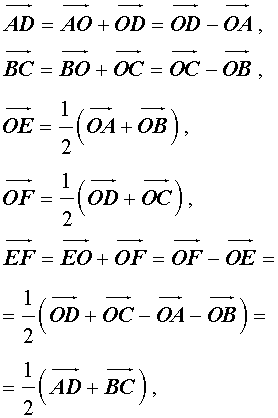Как найти длину средней линии в квадрате

Все формулы средней линии трапеции

Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.

1. Формула средней линии трапеции через основания

b — верхнее основание

a — нижнее основание

m — средняя линия

Формула средней линии, ( m ):

2. Формулы средней линии через основание, высоту и углы при нижнем основании

b — верхнее основание

a — нижнее основание

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, ( m ):

3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

α , β — углы между диагоналями

d ₁ , d ₂ — диагонали трапеции

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции , ( m ):

4. Формула средней линии трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

m — средняя линия

Как найти среднюю линию треугольника?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Средние линии

Средние линии треугольника

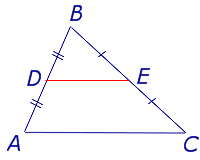
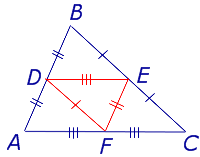
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

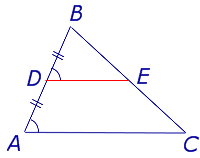
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

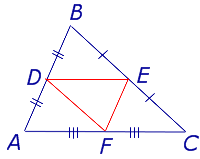
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

• Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
• Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

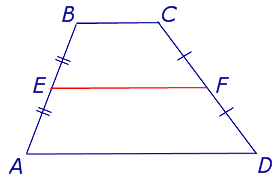
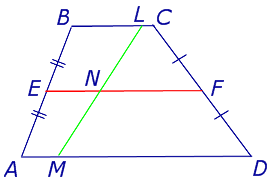
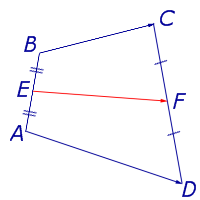
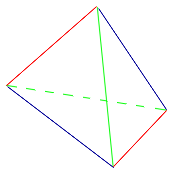
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

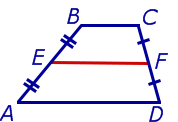
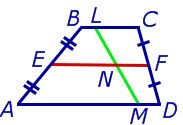
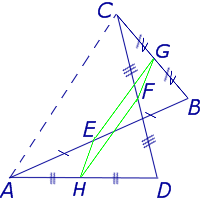
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

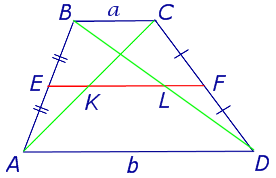
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

что и требовалось доказать.

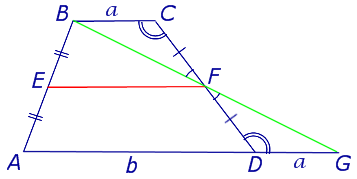
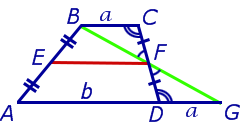
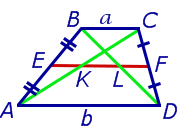
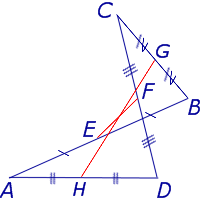
Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

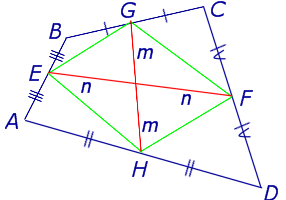
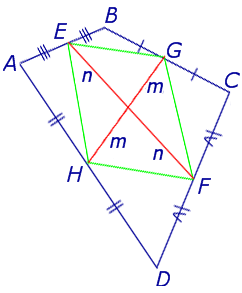
Средние линии четырехугольника. Теорема Вариньона

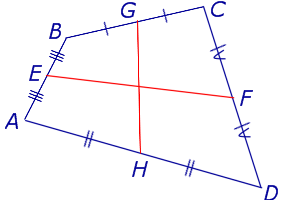
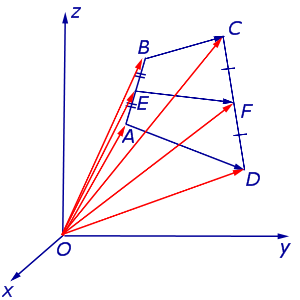
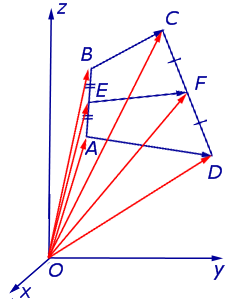
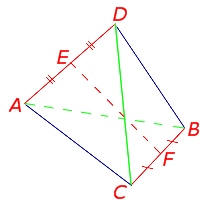
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

На рисунке 10 средние линии – это отрезки EF и GH .

Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

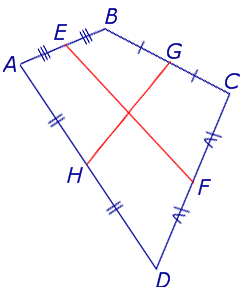
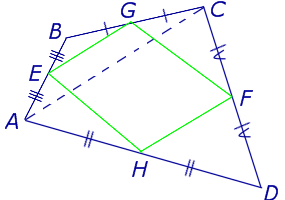
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

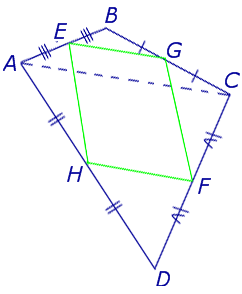
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.
   
   
   
2. Диагонали квадрата равны и пересекаются под прямым углом.
   
   
3. Диагонали квадрата делятся точкой пересечения пополам.
   
4. Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
   
   
5. Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:
   
   

Периметр квадрата P в 4 раза больше его стороны и равен: 

Площадь квадрата равна квадрату его стороны: .

Теорема 1. Диагональ квадрата равна произведению его стороны на , то есть
.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме

Тогда , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна .

Решение:

Мы знаем, что . Тогда .

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

Тогда по формуле площади квадрата:

Второй способ решения:

Воспользуемся формулой для площади ромба:

Ответ: 0,5

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной .

Решение:

Радиус описанной окружности равен половине диагонали квадрата, поэтому

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Решение:

Диаметр окружности равен стороне квадрата: .

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

Поэтому

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата: 

Периметр квадрата со стороной 3 равен: 

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью .

Решение:

Площадь круга  откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными .

 

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .

Ответ: 5.

Стороны квадрата 15, как найти середину?

А если надо тебе найти длину то по теореме пифагора это равно 15корень из 2.

Если если расстояние от середины до стороны то 15 корень из 2 раздели на 2.

K, L, N, M — середины сторон квадрата ABCD ; AC = 10 см?

K, L, N, M — середины сторон квадрата ABCD ; AC = 10 см.

Найти периметр KMNL.

Найти периметр KMNL, помогите, пожалуйста).

Диагонали квадрата ABCD пересекаются в точке o k середина стороны ab найти велечину угла aok?

Диагонали квадрата ABCD пересекаются в точке o k середина стороны ab найти велечину угла aok.

Длина стороны квадрата АВСD равна 6 см?

Длина стороны квадрата АВСD равна 6 см.

Точка М удалена от каждой вершины на 17 см.

Найдите расстояние от, середины отрезка МА до середины каждой из сторон квадрата.

У квадрата с диагональю 6 см последовательно соединили отрезки середины сторон?

У квадрата с диагональю 6 см последовательно соединили отрезки середины сторон.

Найти периметр образовавшегося четырехугольника.

Дан квадрат со стороной 2 см?

Дан квадрат со стороной 2 см.

Точка S отдалёная от каждой из вершин квадрата на 2 см.

Найти расстояние от середины отрезка SC до середины стороны AD квадрата.

Сторона квадрата равна а?

Сторона квадрата равна а.

Если соединить середины смежных сторон и противоположную вершину квадрата, то площадь полученного треугольника равна.

Найти объем тела, полученного при вращении квадрата со сторонами 7 см вокруг прямой, проходящей через середины его противоположных сторон?

Найти объем тела, полученного при вращении квадрата со сторонами 7 см вокруг прямой, проходящей через середины его противоположных сторон.

В квадрате АВСД точка К середина стороны ВС, точка М середина стороны АВ?

В квадрате АВСД точка К середина стороны ВС, точка М середина стороны АВ.

Докажите что прямые АК и МД взаимно перпендикулярны.

Дан квадрат со стороной 6 см?

Дан квадрат со стороной 6 см.

Точка S удалена от каждой вершины квадрата на 7 см.

Найдите расстояние от середины отрезка SA к середине стороны CD квадрата.

Площадь квадрата равна 12?

Площадь квадрата равна 12.

Найдите площадь квадрата, вершинами которого являются середины сторон данного квадрата.

На этой странице находится вопрос Стороны квадрата 15, как найти середину?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 10 — 11 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

Б — да, ответствующие углы раны, В — да, сумма соседних углов = 180 градусов а — нет . Накрест лежащие углы не равны г — нет, сумма соседних углов не равна 180 градусов.

Помойму 30 но это не точно.

Нет, не всегда теоремы равенства треугольников знаешь .

Получ. Они образуют перпендикуляр.

Давайте я попробую помочь. : ).

1. нехай АВС — рівнобедрений трикутник ; АС = 4 см, АВ = 11см ; ВС = АВ = 11 см(АВС рівнобедрений), тоді Р = АВ + ВС + АС = 11 + 11 + 4 = 26(см) 2. Нехай АВС — рівнобедрений трикутник ; АС = 8см, Р = 26см ; у рівнобедреному трикутнику бічні сторони ..

Короче, вот тебе решение с чертежом. Я сама пыталась решить, но ничо не поняла) ответ скорее всего удалят.

Рисунка не будет, ибо там рисовать нечего. Обычный треугольник АВС только с продолженной стороной АС, там и будет угол в 150° Дано : ΔАВС — равносторонний. ∠С(внешний) = 150° Найти : ∠В Решение : 1)∠С = 180° — 150° = 30° (смежные углы) 2)∠А = ∠С = ..

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Перечислим свойства квадрата:

1. Все углы квадрата — прямые, все стороны квадрата — равны.
2. Диагонали квадрата равны и пересекаются под прямым углом.
3. Диагонали квадрата делят его углы пополам.

Площадь квадрата, очевидно, равна квадрату его стороны: .
Диагональ квадрата равна произведению его стороны на , то есть
.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

1 . Найдите сторону квадрата, диагональ которого равна .

Мы знаем, что . Тогда .

2 . Найдите радиус окружности, описанной около квадрата со стороной, равной .

Очевидно, радиус окружности равен половине диагонали квадрата.

3 . Найдите сторону квадрата, описанного около окружности радиуса .

Диаметр окружности равен стороне квадрата.

4 . Найдите радиус окружности, вписанной в квадрат , считая стороны квадратных клеток равными .

Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.

5 . Найдите радиус окружности, вписанной в четырехугольник . В ответе укажите
.

Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, . Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .

Квадрат, свойства и формулы, площадь и периметр

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат (понятие, определение), диагональ квадрата:

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Квадрат – это четырехугольник, имеющий равные стороны и углы.

Все углы квадрата прямые. Каждый из них прямой и равен 90°.

Таким образом, все квадраты отличаются друг от друга только длиной стороны.

Рис. 2. Квадрат и диагонали квадрата

Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.

Квадрат является одновременно частным случаем других фигур: параллелограмма, ромба и прямоугольника. Поэтому квадрату присущи все свойства параллелограмма, ромба и прямоугольника .

Квадрат – это равносторонний прямоугольник.

Квадрат – это ромб с прямыми углами.

Свойства квадрата:

1. Длины всех сторон равны.

2. Противоположные стороны квадрата параллельны.

3. Все углы квадрата прямые. Каждый из них равен 90°.

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

6. Диагонали квадрата взаимно перпендикулярны.

7. Диагонали квадрата точкой пересечения делятся пополам.

8. Угол между диагональю и стороной квадрата равен 45 градусам.

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

Обе диагонали делят квадрат на 4 равных равнобедренных прямоугольных треугольника .

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Формулы квадрата. Площадь квадрата. Периметр квадрата:

Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.

Формула диагонали квадрата:

, , , , .

Формула радиуса вписанной окружности квадрата:

Радиус вписанной окружности квадрата равен половине его стороны.

.

Формула радиуса описанной окружности квадрата:

.

Формула периметра квадрата:

, , .

Формула площади квадрата:

, , , , .

Ответов на вопрос о том, что такое квадрат, может быть множество. Все зависит от того, кому вы этот вопрос адресовали. Музыкант скажет, что квадрат — это 4, 8, 16, 32 такта или джазовая импровизация. Ребенок — что это игра с мячом или детский журнал. Печатник отправит вас изучать кегли шрифта, а техник — разновидности металлопрокатного профиля.

Много и других значений у этого слова, но сегодня мы зададим вопрос математику. Итак…

Разбираться с этой фигурой мы будем постепенно, от простого к сложному, и начнем с истории квадрата. Как он появился, как его воспринимали люди, ученые разных стран и цивилизаций?

История изучения квадрата

Древний мир воспринимает квадрат, главным образом, как четыре стороны света. Вообще, несмотря на множество четырехугольников, именно у квадрата главное число — четыре. Для ассирийцев и перуанцев квадрат — весь мир, то есть он представляет четыре основных направления, стороны света.

Даже Вселенную представляли как квадрат, еще и разделенный на четыре части — это видение жителей Северной Америки. Для кельтов вселенная — это целых три квадрата, вложенных друг в друга, а из центра вытекают четыре (!) реки. А египтяне вообще обожествляли эту фигуру!

Впервые описали квадрат посредством математических формул греки. Но для них этот многоугольник обладал только отрицательными характеристиками. Пифагор вообще не любил четные числа, видя в них слабость и женственность.

Даже в религиях присутствует квадрат. В Исламе Кааба — пуп Земли — имеет не какую-нибудь сферическую, а именно кубическую форму.

В Индии главной графемой, изображающей Землю, или символом земли, был перекрещенный квадрат. И снова речь идет о четырех сторонах света, четырех областях земли.

В Китае квадрат — это мир, гармония и порядок. Хаос побеждается построением квадратной Вары. А квадрат, вписанный в круг, является основой видения мира, символизируя единство и связь Космоса и Земли.

Языческая Русь — Квадрат Сварога. Этот символ еще называют Звездой Сварога, или Звездой Руси. Он довольно сложный, так как составлен из пересекающихся и замкнутых линий. Сварог — бог-Кузнец, самый главный творец, создатель и само небо в представлении русичей. В этом символе есть ромб, что опять говорит о Земле и четырех ее направлениях. И звезда с четырьмя лучами — 4 стороны света, 4 лика Сварога — его всеведение. А пересечение лучей — очаг.

Интересное о квадрате

Самое популярное словосочетание, которое приходит в голову о нашем главном герое — «Черный Квадрат».

Картина Малевича до сих пор очень популярна. Сам автор после ее создания долго мучился вопросом о том, что же это такое, и почему простой черный квадрат на белом фоне так притягивает внимание к себе.

Но если вы приглядитесь внимательно, то заметите, что плоскость квадрата не гладкая, а в трещинах черной краски есть множество разноцветных оттенков. Видимо, вначале была некая композиция, которая автору не понравилась, и он закрыл ее от наших глаз этой фигурой. Черный квадрат, как ничто — черная дыра, только магической квадратной формы. А пустота, как известно, притягивает…

Еще очень популярны «магические квадраты». По сути это — таблица, естественно, квадратная, заполненная числами в каждой графе. Сумма этих чисел одинакова во всех строках, столбцах и диагоналях (по отдельности). Если диагонали исключаются из равенства, то квадрат – полумагический.

Альбрехт Дюрер в 1514 году создал картину «Меланхолия I», на которой изобразил магический квадрат 4х4. В нем сумма чисел всех столбцов, строк, диагоналей и даже внутренних квадратов равна тридцати четырем.

На базе этих таблиц появились очень интересные и популярные головоломки — «Судоку».

Египтяне первыми стали проводить линии взаимосвязи чисел (дата рождения) и качеств характера, способностей и талантов человека. Пифагор взял эти знания, несколько переработал и поместил в квадрат. Получился Квадрат Пифагора.

Это уже отдельное направление в нумерологии. Из даты рождения человека путем сложений высчитывают четыре основных числа, которые помещают в психоматрицу (квадрат). Так и раскладывают все тайные сведения о вашей энергии, здоровье, таланте, удаче, темпераменте и прочем по полочкам. В среднем, по опросам достоверность составляет 60%-80%.

Что такое квадрат?

Квадратом называют геометрическую фигуру. Форма квадрата — четырехугольник, который имеет равные стороны и углы. Еще точнее, этот четырехугольник называют правильным.

У квадрата есть свои признаки. Это:

• стороны, равные по длине;
• равные между собой углы — прямые (по 90 градусов).

В силу этих признаков и особенностей в квадрат можно вписать окружность и описать ее вокруг него. Описанная окружность будет касаться всех его вершин, вписанная — середины всех его сторон. Их центр будет совпадать с центром квадрата и разделит все его диагонали пополам. Последние, в свою очередь, равны между собой и делят углы квадрата на равные части.

Одна диагональ разделяет квадрат на два равнобедренных треугольника, обе — на четыре.

Таким образом, если длина стороны квадрата — t, длина радиуса описанной окружности — R, а вписанной — r, то

• площадь основания квадрата, или площадь квадрата (S) будет равна S=t²=2R²=4r²;

• периметр квадрата P следует вычислять по формуле P=4t=4√2R=8r;

• длину радиуса описанной окружности R=(√2/2)t;

• вписанной — r=t/2.

Площадь основания квадрата еще можно вычислить, зная его сторону (a) или длину его диагонали (c), тогда формулы будут выглядеть соответственно: S=a² и S=1/2c².

Что такое квадрат, мы с вами выяснили. Давайте подробнее рассмотрим детали, ведь фигура квадрат самый симметричный четырехугольник. У него пять осей симметрии, причем одна (четвертого порядка) проходит через центр и является перпендикуляром к плоскости самого квадрата, а четыре другие — оси симметрии второго порядка, две из них параллельны сторонам, а еще две проходят через диагонали квадрата.

Способы построения квадрата

Исходя из определений, кажется, что нет ничего проще, чем построить правильный квадрат. Это так, но при условии, что у вас есть все измерительные инструменты. А если чего-то нет в наличии?

Давайте рассмотрим существующие способы, которые помогут нам построить эту фигуру.

Измерительная линейка и угольник — это основные инструменты, при помощи которых наиболее просто можно построить квадрат.

Сначала отметьте точку, допустим А, от нее мы построим основание квадрата.

С помощью линейки отложите от нее вправо расстояние, равное длине стороны, допустим 30 мм, и поставьте точку Б.

Теперь от обеих точек, воспользовавшись угольником, проведите вверх перпендикуляры по 30 мм каждый. На концах перпендикуляров ставим точки В и Г, которые соединяем между собой, пользуясь линейкой — все, квадрат АБВГ со стороной 30 мм готов!

С помощью линейки и транспортира тоже довольно легко построить квадрат. Начните, как и в предыдущем случае с точки, допустим Н, от нее отложите горизонтальный отрезок, например 50 мм. Поставьте точку О.

Теперь центр транспортира соедините с точкой Н, поставьте отметку у величины угла 90⁰, через нее и точку Н постройте вертикальный отрезок 50 мм, на его конце поставьте точку П. Далее подобным образом постройте третий отрезок от точки О через угол 90⁰, равный 50 мм, пусть он заканчивается точкой Р. Соедините точки П и Р. У вас получился квадрат НОРП с длиной стороны 50 мм.

Можно построить квадрат, пользуясь только циркулем и линейкой. Если вам важен размер квадрата и известна длина стороны, то понадобится еще и калькулятор.

Итак, ставьте первую точку Е — это будет она из вершин квадрата. Далее укажите место, где будет находится противоположная вершина Ж, то есть постойте диагональ ЕЖ вашей фигуры. Если вы строите квадрат по размерам, то имея длину стороны, высчитайте длину диагонали по формуле:

d=√2*a, где a — длина стороны.

После того как вы узнаете длину диагонали, постройте отрезок ЕЖ этой величины. Из точки Е с помощью циркуля в направлении точки Ж проведите полукруг радиусом ЕЖ. И наоборот, из точки Ж — полукруг в сторону точки Е, радиусом ЖЕ. Через точки пересечения этих полукругов, пользуясь линейкой, постройте отрезок ЗИ. ЕЖ и ЗИ пересекаются под прямым углом и являются диагоналями будущего квадрата. Соединив точки ЕИ, ИЖ, ЖЗ и ЗЕ с помощью линейки, вы получите вписанный квадрат ЕИЖЗ.

Еще есть возможность построить квадрат с помощью одной линейки. Что такое квадрат? Это участок плоскости, ограниченный пересекающимися отрезками (линиями, лучами). Следовательно, мы можем построить квадрат по координатам его вершин. Сначала начертите оси координат. Стороны квадрата могут лежать на них, или центр пересечения диагоналей будет совпадать с точкой начала координат — это зависит от вашего желания или условий задачи. Возможно, ваша фигура будет отстоять от осей на некотором расстоянии. В любом случае, сначала отмечаете по числовым значениям (произвольно или условно) две точки, тогда вам будет известна длина стороны квадрата. Теперь можно вычислить координаты оставшихся двух вершин, помня, что стороны квадрата равны и между собой попарно параллельны. Последний шаг — соединить все точки последовательно между собой с помощью линейки.

Какие бывают квадраты?

Квадрат — фигура четко определенная и жестко ограниченная своими определениями, поэтому виды квадратов не отличаются многообразием.

В Неевклидовой геометрии квадрат воспринимается более широко — это четырехугольник с равными сторонами и углами, но градус углов не задан. Это значит, что углы могут быть и по 120 градусов («выпуклый» квадрат) и, например, по 72 градуса («вогнутый» квадрат).

Если вы спросите, что такое квадрат, у геометра или информатика, вам ответят, что — это полный или планарный граф (графы с К₁ по К₄). И это абсолютно справедливо. У графа есть вершины и ребра. Когда они встают в упорядоченную пару, образуется граф. Число вершин — это порядок графа, число ребер — его размер. Таким образом, квадрат — это планарный граф с четырьмя вершинами и шестью ребрами, или К₄:6.

Сторона квадрата

Одно из главных условий существования квадрата — наличие равных по длине сторон — делает сторону очень важной для различных вычислений. Но в то же время дает много способов, чтобы длина стороны квадрата была вычислена при наличии самых разных исходных данных.

Итак, как найти значение стороны квадрата?

• Если вам известна только длина диагонали квадрата d, то вычислить сторону можно по следующей формуле: a=d/√2.
• Диаметр вписанной окружности равен стороне квадрата и, следовательно, двум радиусам, то есть: a=D=2R.
• Радиус описанной окружности тоже может помочь вычислить, чему равна сторона квадрата. Мы можем по радиусу R узнать диаметр D, который, в свою очередь, равен диагонали квадрата d, а формулу для стороны квадрата через диагональ мы уже знаем: a=D/√2=d/√2=2R/√2.
• Из равенства сторон следует, что узнать сторону квадрата (a) можно при помощи его периметра P или площади S: a=√S=P/4.
• Если мы знаем длину линии, которая выходит из угла квадрата и пересекает середину его смежной стороны C, то нам также удастся узнать, какова же длина стороны квадрата: a=2C/√5.

Вот сколько способов существует, чтобы выяснить такой важный параметр, как длина стороны квадрата.

Объем квадрата

Сама фраза является абсурдом. Что такое квадрат? Это плоская фигура, имеющая всего два параметра — длину и ширину. А объем? Это количественная характеристика пространства, которое занимает объект, то есть ее можно вычислить только у объемных тел.

Объемное тело, всеми гранями которого являются квадраты, — куб. Несмотря на колоссальное и принципиальное различие, школьники довольно часто пытаются вычислить объем квадрата. Если это кому-то удастся, Нобелевская премия обеспечена.

А чтобы узнать объем куба V, достаточно перемножить все три его ребра — a, b, c: V=a*b*c. А так как они по определению равны, то формула может выглядеть иначе: V=a³.

Величины, части и характеристики

У квадрата, как и у любого многоугольника, есть вершины — это точки, в которых пересекаются его стороны. Вершины квадрата лежат на описанной вокруг него окружности. Через вершину в центр квадрата проходит диагональ, которая также является биссектрисой и радиусом описанной окружности.

Так как квадрат — это плоская фигура, то рассечь и построить сечение квадрата невозможно. Зато он может быть результатом пересечения многих объемных тел плоскостью. Например, цилиндра. Осевое сечение у цилиндра — прямоугольник или квадрат. Даже при пересечении тела плоскостью под произвольным углом может получиться квадрат!

Но у квадрата есть еще одно отношение к сечению, да не к какому-нибудь, а к Золотому сечению.

Все мы знаем, что Золотое сечение — это пропорция, в которой одна величина относится к другой так же, как их сумма к большей величине. В обобщенном процентном выражении это выглядит следующим образом: исходная величина (сумма) делится на 62 и 38 процентов.

Золотое сечение очень популярно. Оно используется в дизайне, архитектуре, да где угодно, даже в экономике. Но это далеко не единственная пропорция, выведенная Пифагором. Есть, например, еще выражение «√2». На его основе проводится построение динамических прямоугольников, которые, в свою очередь, являются основоположниками форматов группы А (А6, А5, А4 и т.п.). Почему речь зашла о динамических прямоугольниках? Потому что их построение начинается с квадрата.

Да, для начала вам нужно построить квадрат. Его сторона будет равна меньшей стороне будущего прямоугольника. Затем необходимо провести диагональ этого квадрата и, воспользовавшись циркулем, длину этой диагонали отложить на продолжении стороны квадрата. Из полученной на пересечении точки выстраиваем прямоугольник, у которого снова строим диагональ и откладываем ее длину на продолжении стороны. Если продолжить работу по этой схеме, получатся те самые динамические прямоугольники.

Отношение длинной стороны первого прямоугольника к короткой будет 0,7. Это почти 0,68 в Золотом сечении.

Углы квадрата

Собственно, что-то свежее сказать об углах уже сложно. Все свойства, они же признаки квадрата, мы перечислили. Что касается углов, их четыре (как и во всяком четырехугольнике), каждый угол в квадрате — прямой, то есть имеет размер девяносто градусов. По определению, существует лишь прямоугольный квадрат. Если углы большего или меньшего размера — это уже другая фигура.

Диагонали квадрата делят его углы пополам, то есть являются биссектрисами.

Уравнение квадрата

При необходимости вычислить значение различных величин у квадрата (площади, периметра, длин сторон или диагоналей) используют различные уравнения, которые выводятся из свойств квадрата, основных законов и правил геометрии.

1. Уравнение площади квадрата

Из уравнений для вычисления площади четырехугольников мы знаем, что она (площадь) равна произведению длины и ширины. А так как стороны квадрата одинаковые по длине, то площадь его будет равна длине любой стороны, возведенной во вторую степень

S=a².

Используя теорему Пифагора, мы можем вычислить площадь квадрата, зная длину его диагонали.

S=d²/2.

2. Уравнение периметра квадрата

Периметр квадрата, как и всех четырехугольников, равен сумме длин его сторон, а так как они все одинаковые, то можно сказать, что периметр квадрата равен длине стороны, умноженной на четыре

P=a+a+a+a=4a.

Снова теорема Пифагора поможет нам найти периметр через диагональ. Нужно значение длины диагонали умножить на два корня из двух

P=2√2d

3. Уравнение диагонали квадрата

Диагонали квадрата равны, пересекаются под прямым углом и делятся точкой пересечения пополам.

Найти их можно, исходя из вышеприведенных уравнений площади и периметра квадрата

d=√2*a, d=√2S, d=P/2√2

Есть еще способы узнать, какова же длина диагонали квадрата. Радиус вписанной в квадрат окружности равен половине его диагонали, отсюда

d=√2D=2√2R, где D — диаметр, а R — радиус вписанной окружности.

Зная радиус описанной окружности, рассчитать диагональ еще проще, ведь она является диаметром, то есть d=D=2R.

Также есть возможность вычислить длину диагонали, зная длину линии, выходящей из угла к центру стороны квадрата C: d=√8/5*C.

Но не стоит забывать, что квадрат — это участок плоскости, ограниченный четырьмя пересекающимися линиями.

Для линий (и образованных ими фигур) существует достаточно уравнений, не нуждающихся в дополнительном описании, но линия бесконечна. А многоугольники ограничены пересечением линий. Для них можно использовать линейные уравнения, объединенные в систему, задающие прямые линии. Но необходимо указывать дополнительные параметры, условия.

Для определения многоугольников же необходимо составить такое уравнение, которое бы описывало не линию, а отдельный произвольный отрезок без вмешательства дополнительных условий и описаний.

[ x/x_i ]*[ x_i/x]*y_i — вот это специальное уравнение для многоугольников.

Квадратные скобки в нем указывают на условие исключения дробной части числа, то есть мы должны оставить только целое число. y_i — функция, которая выполнятся в диапазоне параметра от x до x_i.

Используя это уравнение, можно вывести новые уравнения для вычисления отрезков и линий, состоящих из нескольких отрезков. Оно является базовым, универсальным для многоугольников.

Помним, что квадрат — это часть плоскости, поэтому его описание типа y=f(x) можно представить, чаще всего, только как многозначную функцию, которую, в свою очередь, можно выразить через однозначные, если представлять их параметрически, то есть зависящими от какого-либо параметра t:

x=f(t), y=f(t).

Так вот, если использовать в совокупности универсальное уравнение и параметрическое представление, то действительно можно вывести уравнение для выражения многоугольников:

x=((A2+A3)*A5+A4*P)*Cos(L)

y=((A1+A4)*A5+A3*P)*Sin(L),

где

A1=[1/[T/P]]*[T/P]; A2=[2/[T/P]]*[[T/P]/2]; A3=[3/[T/P]]*[[T/P]/3]; A4=[4/[T/P]]*[[T/P]/4]; A5=T-P*[T/P],

где P — диагональ прямоугольника, L — угол наклона к горизонтали диагонали P, T — параметр изменяющийся в диапазоне от P до 5P.

Если L=3,14/4, то уравнение будет описывать квадраты разной величины, в зависимости от размера диагонали P.

Применение квадрата

В современном мире технологии позволяют придавать различным материалам квадратную форму, точнее квадратное сечение.

Это во многом выгоднее, дешевле, долговечнее и безопаснее. Так, сейчас делают квадратные трубы, сваи, проволоку (провода) и даже квадратные нити.

Основные преимущества очевидны, они выходят из элементарной геометрии. При одинаковом размере площадь вписанного круга меньше площади квадрата, в который он вписан, следовательно, пропускная способность квадратной трубы или энергоемкость квадратного провода будут выше, чем у круглых аналогов.

Зачастую расходные материалы квадратного сечения более эстетичны и удобны в использовании, монтаже, креплении.

При выборе этих материалов важно правильно рассчитать сечение квадрата, чтобы провод или труба выдержали необходимую нагрузку. В каждом отдельном случае, конечно, будут необходимы такие параметры, как сила тока или давление, но и без основных геометрических правил квадрата тут не обойтись. Хотя размеры квадратных сечений уже не столько вычисляют, сколько выбирают по заданным параметрам из таблиц, установленных ГОСТами для разных отраслей.