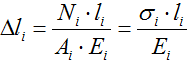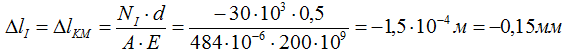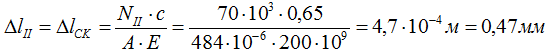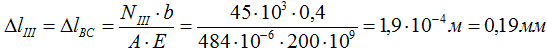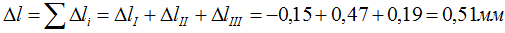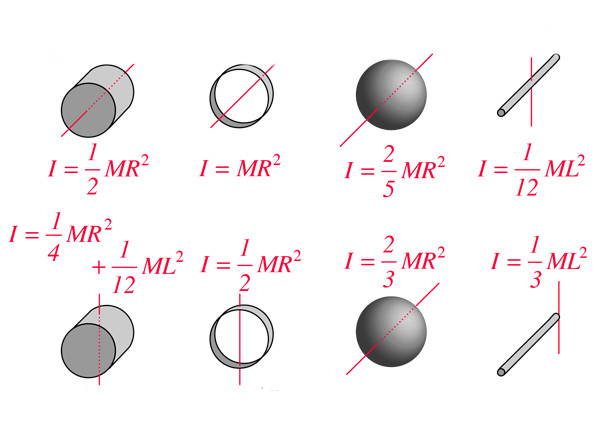Как найти длину стержня через массу

Как найти длину через массу

Масса определяется плотностью материала и объемом, которое занимает физическое тело в пространстве, поэтому обойтись одним лишь значением массы, увы, не получится. Если кроме нее доступны данные о материале пространственного объекта, то можно выяснить соответствующую ему плотность вещества. Тогда неизвестным останется лишь объем, одной из характеристик которого и является длина. Ниже приведены несколько способов определения длины для пространственных фигур правильной формы, при условии, что средняя плотность вещества известна.

Инструкция

Если пространственный объект имеет форму тора (цилиндра), то для определения его длины (L) необходимо знать площадь основания. Вычислить его можно, имея сведения о диаметре (d) тора. Если они есть, то используйте тот факт, что объем, с одной стороны равен отношению массы (m) к плотности (p), а с другой — четверти от произведения числа Пи на длину и возведенный в квадрат диаметр: m/p=¼*π*d²*L. Из этого тождества вытекает, что высота будет равна частному от деления учетверенной массы на произведение плотности на число Пи и квадрат диаметра: L=m*4/(p*π*d²).

Если пространственная фигура представляет собой брус (прямоугольный параллелепипед) то площадь основания можно посчитать, зная ширину (w) и высоту (h), а если сечение имеет форму квадрата, то достаточно и одной стороны. В этом случае объем будет равен произведению длины на ширину и высоту и можно, как и на предыдущем шаге, составить тождество: m/p=w*h*L. Выведите из него значение высоты — она будет равна частному от деления массы на произведение плотности, ширины и высоты: L=m/(p*w*h).

Если объемная фигура имеет в сечении форму равностороннего треугольника, то для вычисления объема измерьте ширину одной грани (a), то есть сторону треугольника сечения. Площадь такого треугольника вычисляется умножением четверти от возведенной в квадрат длины стороны на квадратный корень из тройки, а для определения объема надо умножить результат на искомую длину (в данном случае ее правильнее назвать высотой). Вновь подставьте это значение в тождество: m/p=L*3*a²/4. Выведите из этого равенства формулу для вычисления длины — она будет представлять собой соотношение учетверенной массы и утроенного произведения плотности на квадрат стороны треугольника: L=4*m/(3*p*a²).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

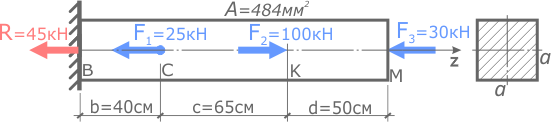
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.

Предыдущие пункты решения задачи

Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.

Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:

где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.

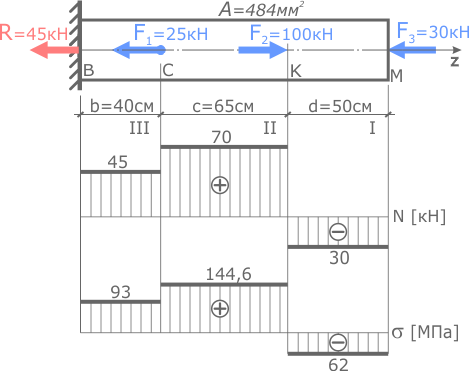
Значения внутренних сил и напряжений принимаются с построенных эпюр N ( σ ).

По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δ l второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).

Деформация I участка (KM)

Удлинение третьего участка BC

Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:

В результате деформации общая длина стержня увеличится на 0,51мм.

Разобранные примеры показывают, что критическое значение сжимающего осевого усилия на стержень можно выразить по формуле

где — приведенная длина стержня. Коэффициенты приведения: — шарнирное закрепление обоих концов, — консольный стержень, — стержень с двумя заделками, — стержень с заделкой и шарнирной опорой.

Формула (207) называется обобщенной формулой Эйлера. Напомним, что она справедлива, если напряжения и деформации в стержне в момент потери устойчивости находятся в упругой области:

где — предел пропорциональности материала. Величина

называется минимальным радиусом инерции поперечного сечения.

Введем еще одно важное понятие — гибкость стержня

Тогда обобщенную формулу Эйлера можно представить в простой форме:

Условие (208) ограничивает область применения формулы Эйлера.

Минимальное значение гибкости, ниже которой формула Эйлера перестает быть пригодной, равно

Например, для малоуглеродистой стали при и

Формулу Эйлера можно применять, если .

Замечание. Критическое напряжение, конечно, является сжимающим. В задачах устойчивости по традиции, чтобы устранить знак «минус» в расчетных формулах, критические сжимающие напряжения считаются положительными.

Рис. 12.40. Устойчивость стержня переменного сечения

В момент потери устойчивости сжатый стержень выпучивается, поворачивается вокруг центров соответствующих узлов и вследствие жесткости фасонок заставляет поворачиваться и изгибаться в плоскости фермы остальные стержни.

Примыкающие стержни сопротивляются изгибу и повороту узла и препятствуют свободному изгибу стержня, теряющего устойчивость.

Наибольшее сопротивление повороту узла оказывают растянутые стержни. Сжатые стержни слабо сопротивляются изгибу.

Таким образом, чем больше растянутых стержней примыкает к сжатому стержню и чем они мощнее (больше их погонная жесткость), тем выше степень защемления стержня и меньше его расчетная длина; влиянием сжатых стержней на защемление можно пренебречь.

Сжатый пояс оказывается слабо защемленным в узлах, так как с каждой стороны к нему примыкает только по одному растянутому раскосу, погонная жесткость которых значительно меньше погонной жесткости пояса. Поэтому защемлением сжатого пояса в запас устойчивости можно пренебречь и принимать его расчетную длину равной расстоянию между смежными узлами.

Таким образом, при большей степени защемления меньше расчетная длина стержня фермы: ,

где — коэффициент приведения длины, зависящий от степени защемления;

— расстояние между центрами узлов.

По нормам коэффициент приведения длины “” элементов решетки из уголков в плоскости фермы равен 0,8. Тогда расчетная длинав плоскости фермы определяется с некоторым запасом, в особенности для средних раскосов, жесткость которых по сравнению с примыкающими стержнями невелика.

Исключение составляет опорный восходящий раскос, условия работы которого в плоскости фермы такие же, как и у верхнего пояса, поэтому расчетная длина опорного раскоса в плоскости фермы принимается равной расстоянию между центрами узлов.

Расчетная длина пояса в плоскости, перпендикулярной плоскости фермы, принимается равной расстоянию между узлами, закрепленными связями от смещения из плоскости фермы.

В беспрогонных покрытиях верхний пояс стропильных ферм закреплен в плоскости кровли плитами или панелями настила, прикрепленными к поясам ферм в каждом узле. В этом случае за расчетную длину пояса из плоскости фермы принимают ширину одной плиты.

Расчетная длина стержней решетки при выгибе их из плоскости фермы принимается равной расстоянию между геометрическими центрами узлов, так как фасонки очень гибки и рассматриваются как листовые шарниры.

В трубчатых фермах с бесфасонными узлами расчетная длина раскоса, как в плоскости фермы, так и из нее, с учетом повышенной крутильной жесткости замкнутых сечений применятся равной 0,9.

В других случаях расчетная длина элементов ферм принимается по нормали.

9.7. Предельные гибкости стержней

Элементы конструкций должны проектироваться из жестких стержней. Особенно существенное значение имеет гибкость “” для сжатых стержней, теряющих устойчивость при продольном изгибе.

Даже при незначительных сжимающих усилиях гибкость сжатых стержней не должна быть слишком большой, так как гибкие стержни легко искривляются от случайных воздействий, провисают, вибрируют при динамических нагрузках. Поэтому для сжатых стержней устанавливается предельная гибкость, зависящая от назначения стержня и степени его нагружения , где— расчетное усилие,— несущая способность стержня:

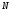
сжатые пояса, а также опорные стойки и раскосы,

передающие опорные реакции……………………………………………… 180-60

прочие сжатые стержни фермы………………………………………………… 210-60

При этом принимается не менее 0,5.

Растянутые стержни конструкций так же не должны быть слишком гибкими, так как могут прогнуться при транспортировании и монтаже.

Стержни должны иметь достаточную жесткость особенно в конструкциях подверженных динамическим воздействиям.

Для растянутых стержней ферм, подвергающихся действию динамической нагрузки, установлены следующие значения предельной гибкости:

растянутые пояса и опорные раскосы………………………………………250

прочие растянутые стержни ферм………………………………………….350

растянутые стержни связей………………………………………………….400

В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых стержней ограничивают только в вертикальной плоскости (чтобы предотвратить чрезмерное провисание), установив для всех растянутых стержней предельную гибкость .

32. Типы, подбор и проверка сечений стержней ферм. Конструирование, особенности работы и расчета узлов ферм из парных уголков.

В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику — момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.

Вращение и момент инерции

Инерции момент проще всего ввести для материальной точки. Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:

I = M*R².

Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:

I = ∫_m(r²*dm).

Через объем и плотность это равенство записывается в таком виде:

I = ∫_V(ρ*r²*dV).

Его часто применяют для вычисления значений I конкретных геометрических объектов.

Физический смысл инерции момента I заключается в том, что он определяет, насколько «сложно» данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.

Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, — это закон сохранения момента импульса. Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.

Тонкий стержень и оси вращения

Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной. Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.

Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.

Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O₁, вторая — через конец стержня, обозначим ее O₂. Относительно них и вычислим величину I.

Момент инерции относительно O1

В первую очередь выпишем общую формулу. Имеем:

I = ∫_V(ρ*r²*dV).

Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.

Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:

I = ∫_L(ρ*S*l²*dl).

Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O₁ проходит через середину стержня, то пределы интегрирования будут следующими:

I = ∫_-L/2^L/2(ρ*S*l²*dl).

Результатом вычисления этого интеграла является следующая формула:

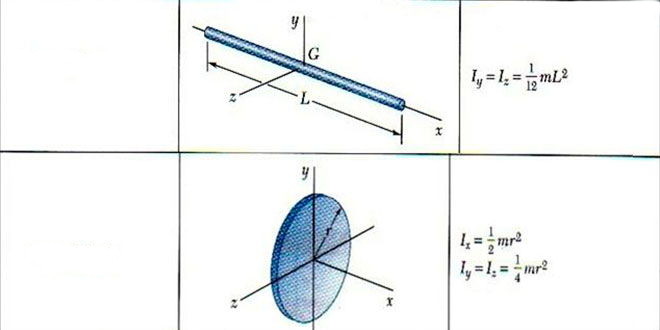
I = M*L²/12.

Таким образом, момент инерции тонкого стержня определяется его массой и длиной.

Инерции момент относительно O2

Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.

Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:

I = I₀ + M*h².

Здесь I₀ — момент инерции стержня относительно оси O, h — дистанция между осями.

Эту формулу можно с успехом применить для нашего случая. Поскольку I₀ мы рассчитали в предыдущем пункте статьи относительно оси O₁, и расстояние между O₁ и O₂ составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:

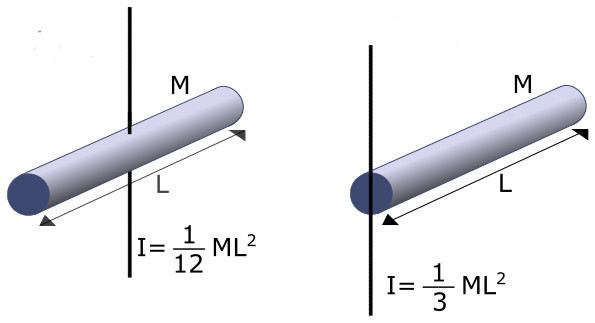
I = I₀ + M*h² = M*L²/12 + M*L²/4 = M*L²/3.

Таким образом, для стержня величина I относительно оси O₂ в 4 раза больше, чем относительно оси O₁. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O₂ следует приложить в 4 раза больший крутящий момент, чем в случае оси O₁.

Пример задачи

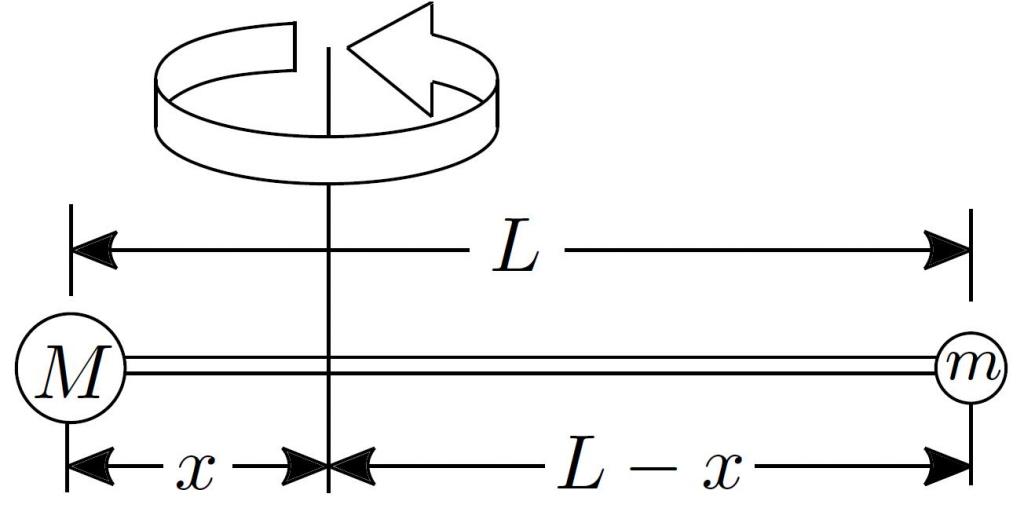
Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?

Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O₁ и заданной в задаче равно:

h = 0,25 — 0,2 = 0,05 м.

Тогда получаем момент инерции стержня (однородного):

I = I₀ + M*h² = 5*0,5²/12 + 5*0,05² = 0,117 кг*м².

В СИ момент инерции стержня измеряется в указанных единицах.

Цель: сформировать представления
учащихся о применении определённого интеграла к
решению прикладных задач.

Рассмотреть примеры применения определенного
интеграла к решению прикладных задач, а именно:

• нахождения перемещения точки за поданный
  промежуток времени;
• вычисления работы, которую нужно выполнить для
  перемещения тела из одной точки в другую;
• вычисления массы неоднородного стержня, если
  известно, как изменяется его линейная плотность;
• вычисления величины заряда, переносимого за
  определенный промежуток через сечение
  проводника.

Работать над формированием умений учащихся
применять определённый интеграл к решению
прикладных задач.

Тип урока: усвоение знаний,
формирование умений.

Ход урока

I. Организационный этап

Проверка готовности учащихся к уроку, настрой
на работу.

II. Проверка домашнего задания

Выборочно проверяем тетради у учащихся,
нуждающихся в дополнительном педагогическом
внимании.

Проверку правильности выполнения упражнений
домашнего затенения осуществляем по образцам,
заранее записанными на доске учителем или
отдельными учащимися.

III. Формулировка цели и задач урока.

Символ интеграла введен с 1675 г., а вопросами
интегрального исчисления занимаются с 1696 г. Хотя
интеграл изучают, в основном, ученые–математики,
но и физики внесли свой вклад в эту науку.

Практически ни одна формула физики не
обходится без дифференциального и интегрального
исчислений.

Поэтому, сегодня на уроке мы рассмотрим
применение интеграла в физике.

Давайте вспомним, какие примеры применения
интеграла нам известны? (Вычисления площадей
плоских фигур и объемов тел).

В этих случаях величины, которые находят, можно
рассматривать как функции отрезка.

Сообщаем, что существуют физические величины,
которые можно рассматривать как функции отрезка.
Например, перемещение вычисляют в зависимости от
отрезка времени движения, работа силы при
движении тела по прямой зависит от пройденного
отрезка пути, электрический заряд, проходящий
через поперечное сечение проводника, зависит от
отрезка времени, за которое проводится измерения
т.п. Эти и другие величины можно вычислить с
помощью определенного интеграла.

Следовательно, задача урока — рассмотреть
примеры применения определенного интеграла к
вычислению величин.

IV. Актуализация опорных знаний.

Выполнение устных упражнений

Вычислите интеграл:

;

;

;

;

;

.

V. Изучение материала.

План изучения темы

• Применение определенного интеграла к решению
  прикладных задач.
• Примеры решения задач с применением
  определенного интеграла.

Пример 1. Тело движется прямолинейно
со скоростью v(t)=(3 +3t²)м/с. Найдите путь,
который пройдет тело за первые 5с.

Решение. По формуле (1) получаем:

.

Ответ. 140м.

Применение определенного интеграла к решению
прикладных задач.

1. Нахождение перемещения точки за данный
промежуток времени. Предположим, что точка
движется по прямой (по оси Ох) и известна скорость
этой точки. Найдем перемещение s точки за
промежуток времени [t₁;t₁].
Рассмотрим отрезок времени [t; t+t] и будем считать скорость на
этом отрезке постоянной. Тогда получим: s(t)=v(t) * t, отсюда: .

2. Вычисление работы, которую нужно выполнить
для перемещения тела из одной точки в другую. Пусть
тело движется по оси Ох, в каждой точке которой
приложена некоторая сила F=F(х). Вычислим работу А,
которую необходимо выполнить при перемещения с
точки х₁ в точку х₂. На малом отрезке
пути от точки х до точки х+х можно считать силу
постоянной, равной F(x). Тогда А(х)=F(x)x. Отсюда получаем, что всю работу на
отрезке [x₁;x₂] можно записать в виде
интеграла: .

3. Вычисление массы неоднородного стержня.
Вычислим массу m неоднородного стержня, если
известно, как меняется его плотность (х). Рассмотрим отрезок
[х; х+?x]. Считая, что на этом отрезке плотность
стержня не изменяется, получим: m(x)=(x)x,
отсюда .

Вычисление величины заряда, переносимого за
определенный промежуток времени через сечение
проводника. Вычислим величину q заряда,
переносимого за промежуток времени [t₁;t₂]
через сечение проводника. Пусть задан закон
изменения тока I=I(t) в зависимости от времени.
Тогда на малом промежутке времени [t;t+t] можно считать силу
тока постоянной, равной I(t), а q=I(t)t. Итак, .

Пример 2. Вычислите работу силы F при
сжатии пружины на 0,06 м, если для ее сжатия на 0,01 м
требуется сила 5Н.

Решение. По закону Гука, сила F пропорциональна
растяжению или сжатию пружины, т.е. F=kx, где х –
величина растяжения или сжатия (в метрах), k —
постоянная. Из условия задачи находим k.
Поскольку при х=0,01м сила F=5Н, то . Итак, F(x)=500x. тогда
по формуле (2): .

Ответ. 0,9Дж.

Изложение нового материала проводим в
зависимости от уровня умственной активности и
математической подготовленности учащихся. Если
уровень умственной активности учащихся не
достаточно высок, то рассматриваем только
некоторые примеры решения задач с помощью
определенных интегралов. В противном случае не
только приводим примеры применения интеграла к
решению практических задач, но и объясняем, какие
именно величины можно вычислять с помощью
определенного интеграла. Проводим беседу, в ходе
которой добиваемся понимания, что для вычисления
величин с помощью интеграла необходимо знать
скорость изменения этих величин. Так, скоростью
изменения перемещения (или расстояния) обычная
скорость. Скоростью изменения работы
зависимости от времени является мощностью, а в
зависимости от перемещения – силой. Скорость
изменения массы тела – это его плотность. Если
первоначальный размер задан в виде некоторой
функции, то ее скорость находим как производную
этой функции. Интеграл применяют тогда, когда
известна скорость изменения начальной величины.
Если искомую величину представить в виде
прироста некоторой функции F, то f является
производной F и соответственно F –
первоначальной для f. Если искомая величина
является приростом первоначальной для функции f
или интегралом от функции f.

Приводим схему применения интеграла:

1) записываем скорость изменения искомой
величины с помощью дифференциалов: dF=f(t)dt (или F=f(t)t);

2) переписываем значение F в виде интеграла: ;

3) вычисляем интеграл известными способами.

VI. формирование умений

Выполнение устных упражнений

Скорость движения тела задано уравнением v(t)=2t-3(м/с).
Найдите расстояние, которое преодолело тело за
первые 5с.

Линейная плотность неоднородного стержня
изменяется по закону р(l)=8l+1(кг/м). Найдите
массу стержня, если его длина равна 50см.

Выполнение письменных упражнений

Тело движется прямолинейно со скоростью v(t)
(м/с). Вычислите путь, который пройдет тело за
промежуток времени от t=t₁ до t=t₂, если:

1) v(t)=3t²+1, t₁=0, t₂=4;

2) v(t)=2t²+t, t₁=1, t₂=3.

Скорость движения тела в момент времени t(с)
задано формулой v=15-3t (м/с). Какой путь преодолеет
тело от начала движения до полной остановки?

Какую работу нужно выполнить для сжатия
пружины на 4 см, если известно, что сила 2Н сжимает
эту пружину на 1см?

Вычислите величину заряда , переносимого через
поперечное сечение проводника за 20с , если сила
тока изменяется по законом I(t)=2t+1(А).

Дополнительные упражнения

1. Вычислите работу, которую необходимо
выполнить, чтобы откачать воду из цилиндрической
цистерны, радиус которой равен R, а высота – Н.

2. Тело массой 2 кг движется прямолинейно под
действием силы F(t)=12t-8(Н). Найдите закон его
движения, если в момент времени t=3с скорость тела
равна 10м/с, а координата 21м.

VII. Итоги урока.

Контрольный вопрос

Приведите примеры применения определенного
интеграла к решению прикладных задач.

VIII. домашнее задание.

Изучить теоретический материал.

Выполнить упражнения.

Скорость движения тела задано уравнением v(t)=1+6t²
(м / с). Найдите расстояние, которое преодолело
тело:

1) за первые 10 с

2) за третью секунду.

Сила 4Н растягивает пружину на 8 см. Какую работу
нужно исполнить, чтобы растянуть пружину на 8 см?

Линейная плотность неоднородного стержня
меняется по закону p(l)=32l+2(кг/м). Найдите массу
стержня, если его длин на равна 25 см.