Как найти длину стержня в системе отсчета

Длина
тел в разных системах отсчета.
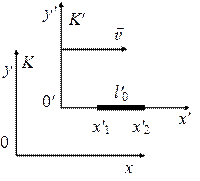
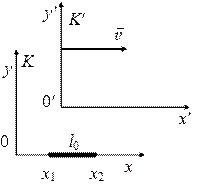
Рассмотрим стержень, расположенный
вдоль оси x’ и
покоящийся относительно системы К’.
Длина стержня в системе К’ равна l’₀ =
x’₂ — x’₁,
где x’₁, x’₂—
не изменяющиеся со временем t’ координаты
начала и конца стержня; индекс 0 показывает,
что в системе K’ стержень
покоится. Определим длину стержня в
системе K,
относительно которой он движется со
скоростью v.
Для этого необходимо измерить координаты
концов стержня x₁ и x₂в
системе K в
один и тот же момент времени t.
Их разность l
= x’₂ — x’₁ и
даст длину стержня в системе К:

      Таким
образом, размер тела, движущегося
относительно инерциальной системы
отсчета, уменьшается в направлении
движения в  раз,
т.е. лоренцево
сокращение длины тем больше, чем больше
скорость движения.

19.Релятивстская кинематика: длина тел и длительность событий в разных системах отсчета, релятивистский закон сложения скоростей.

Длительность
событий в разных системах отсчета.
Пусть в некоторой точке A с
координатойx,
покоящейся относительно системы К,
происходит событие, длительность
которого (разность показаний часов в
конце и начале события) τ
= t₂ — t₁,
где индексы 1 и 2 соответствуют началу
и концу события. Длительность этого же
события в системе К’

      Таким
образом, 

т.е. длительность
события, происходящего в некоторой
точке, наименьшая в той инерциальной
системе отсчета, относительно которой
эта точка неподвижна. Следовательно,
часы, движущиеся относительно инерциальной
системы отсчета, идут медленнее покоящихся
часов,
т.е. ход часов замедляется в системе
отсчета, относительно которой часы
движутся.

Релятивистский
закон сложения скоростей.
Пусть материальная точка движется в
системе К’вдоль
оси x’,
а система К’ движется
относительно К со
скоростью v (оси x и x’ совпадают).
Тогда

      Произведя
вычисления, получим релятивистский
закон сложения скоростей:

      Если
скорости v, u’_x, u_x малы
по сравнению со скоростью света, то эти
формулы переходят в привычный закон
сложения скоростей в классической
механике. Релятивистский закон сложения
скоростей не противоречит второму
постулату Эйнштейна: если u’_x =
c то u_x =
c,
т.е. скорость с –
предельная скорость, которую невозможно
превысить.

20.Понятие о релятивистской механике. Закон взаимосвязи массы и энергии. Кинетическая энергия. Связь между полной энергией и импульсом частицы.

Согласно
представлениям классической механики,
масса тела есть величина постоянная.
Однако в конце XIX в. на опытах с электронами
было установлено, что масса тела зависит
от скорости его движения, а именно
возрастает с увеличением v по
закону

                                                                                                             (5.8)

где m₀ —
масса покоя, т.е. масса материальной
точки, измеренная в той инерциальной
системе отсчета, относительно которой
точка покоится; m –
масса точки в системе отсчета, относительно
которой она движется со скоростью v.
      Из
принципа относительности Эйнштейна,
утверждающего инвариантность всех
законов природы при переходе от одной
инерциальной системы отсчета к другой,
следует, что основной закон динамики
Ньютона

оказывается
инвариантным по отношению к преобразованиям
Лоренца, если в нем справа стоит
производная от релятивистского
импульса:

                                                                               (5.9)

или
                                                                                                                 (5.10)

где
                                                                                (5.11)

      Из
приведенных формул следует, что при
скоростях, значительно меньших скорости
света в вакууме, они переходят в формулы
классической механики. Следовательно,
условием применимости законов классической
механики является условие v
<< c.
Законы Ньютона получаются как следствие
СТО для предельного случая v
<< c.
Таким образом, классическая механика
– это механика макротел, движущихся с
малыми (по сравнению со скоростью света
в вакууме) скоростями.
      Вследствие
однородности пространства в релятивистской
механике выполняется закон
сохранения релятивистского импульса:
релятивистский импульс замкнутой
системы тел сохраняется, т.е. не изменяется
с течением времени.
      Изменение
скорости тела в релятивистской механике
влечет за собой изменение массы, а,
следовательно, и полной энергии, т.е.
между массой и энергией существует
взаимосвязь. Эту универсальную зависимость
– закон
взаимосвязи массы и энергии –
установил А.
Эйнштейн:

                                                                                 (5.12)

      Из
(5.13) следует, что любой массе (движущейся m или
покоящейся m₀)
соответствует определенное значение
энергии. Если тело находится в состоянии
покоя, то его энергия покоя

      Энергия
покоя является внутренней энергией
тела,
которая складывается из кинетических
энергий всех частиц, потенциальной
энергии их взаимодействия и суммы
энергий покоя всех частиц.
      В
релятивистской механике не справедлив
закон сохранения массы покоя. Именно
на этом представлении основано объяснение
дефекта массы ядра и ядерных реакций.
      В
СТО выполняется закон
сохранения релятивистской массы и
энергии:
изменение полной энергии тела (или
системы) сопровождается эквивалентным
изменением его
массы:

                                                         (5.13)

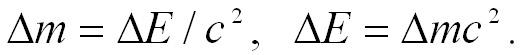
      Таким
образом, масса тела, которая в классической
механике является мерой инертности или
гравитации, в релятивистской механике
является еще и мерой энергосодержания
тела.
      Физический
смысл выражения (5.14) состоит в том, что
существует принципиальная возможность
перехода материальных объектов, имеющих
массу покоя, в электромагнитное излучение,
не имеющее массы покоя; при этом
выполняется закон сохранения
энергии.
      Классическим
примером этого является аннигиляция
электрон-позитронной пары и, наоборот,
образование пары электрон-позитрон из
квантов электромагнитного излучения:

      В
релятивистской динамике значение
кинетической энергии E_k определяется
как разность энергий движущегося E и
покоящегося E₀ тела:

          (5.14)

      При v
<< c уравнение
(5.15) переходит в классическое выражение

      Из
формул (5.13) и (5.11) найдем релятивистское
соотношение между полной энергией и
импульсом
тела:

                                                         (5.15)

      Закон
взаимосвязи массы и энергии полностью
подтвержден экспериментами по выделению
энергии при протекании ядерных реакций.
Он широко используется для расчета
энергического эффекта при ядерных
реакциях и превращениях элементарных
частиц.

2.2.3. Собственная длина и собственный объем[править]

Рассмотрим стержень, который покоится в системе отсчета К и параллельный оси «х». Длина стержня в системе К может быть вычислена:

 формулы (2.2.13)

Найдем длину этого стержня в системе отсчета K’, которая движется относительно К с постоянной скоростью V.

 формулы (2.2.14)

По определению, «собственной длиной» стержня называется его длина в той системе, в которой стержень покоится.

Обозначим собственную длину неподвижного стержня , а длину движущегося стержня обозначим . Эти длины связаны формулой (2.2.14) :

 формулы (2.2.15)

Как видно, самую большую длину стержень имеет в той системе отсчета, в которой он покоится. При движении длина уменьшается, этот эффект называют «Лоренцевым сокращением».

Из выражений (2.2.11)  легко показать, что поперечные размеры тела не изменяются при движении вдоль оси «х». Это означает, что объем тела меняется точно так же, как и его длина:

 формулы (2.2.16)

где V₀ — это «собственный объем» тела.

См. также[править]

<<Назад  |  Далее>>
Оглавление

Примечания[править]

2018-03-24   

Найти собственную длину стержня, если в лабораторной системе отсчета его скорость $v = c/2$, длина $l = 1,00 м$ и угол между ним и направлением движения $theta = 45^{ circ}$.

Решение:

В покоящийся системе отсчета координаты концов стержня в определениях собственной длины $l_{0}$

$A: (0,0,0) B: (l_{0} cos theta_{0}, l_{0} sin theta_{0},0)$

в момент времени $t$. В лабораторной системе отсчета координаты в момент времени $t^{ prime}$

$A: (vt^{ prime}, 0,0), B: left ( l_{0} cos theta_{0} sqrt{1 — beta^{2} } + vt^{ prime}, l_{0} sin theta_{0}, 0 right )$

Поэтому мы можем написать,

$l cos theta_{0} = l_{0} cos theta_{0} sqrt{ 1 — beta^{2} }$ и $l sin theta = l_{0} sin theta_{0}$

следовательно $l_{0}^{2} = l^{2} left ( frac{ cos^{2} theta + (1 — beta^{2} ) sin^{2} theta }{1 — beta^{2} } right )$

или, $ = sqrt{ frac{ 1 — beta^{2} sin^{2} theta }{1 — beta^{2} } }$

Длина отрезка – разность координат его начала и конца, измеренных одновременно в выбранной системе отсчёта.

Отрезок (стержень) расположен вдоль оси x‘ и покоится относительно К’ (рис. 7.7).

Его длина в системе К’:

({l’_0} = {x’_2} — {x’_1};begin{array}{*{20}{c}}{}end{array}{t’_1} = {t’_2}). (7.32)

Система К’ движется относительно системы К со скоростью .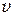

Длина отрезка в системе К

({l’_0} = frac{{{x_2} — v{t_2}}}{{sqrt {1 — {beta ^2}} }} — frac{{{x_1} — v{t_1}}}{{sqrt {1 — {beta ^2}} }} = frac{{{x_2} — v{t_2} — {x_1} + v{t_1}}}{{sqrt {1 — {beta ^2}} }};) (7.33)

при({t_1} = {t_2}) получаем следующее выражение:

({l’_0} = frac{l}{{sqrt {1 — {beta ^2}} }}). (7.34)

Из формулы (7.34) следует, что (l = {l’_0}sqrt {1 — {beta ^2}} ,) т.е.

({l’_0} > l.) (7.35)

Длина стержня ({l’_0}) в системе, относительно которой он покоится, больше длины стержня l в системе, относительно которой он движется.

Стержень покоится в системе К, система К’ движется относительно К со скоростью (v)(рис. 7.8).

В системе К

({l_0} = {x_2} — {x_1};quad {t_1} = {t_2}),

с учетом преобразований

({l_0} = frac{{{{x’}_2} — v{{t’}_2} — {{x’}_1} + v{{t’}_1}}}{{sqrt {1 — {beta ^2}} }} = frac{{l’}}{{sqrt {1 — {beta ^2}} }}).

В системе Кʹ

(l’ = {l_0}sqrt {1 — {beta ^2}} quad Rightarrow quad {l_0} > l’.) (7.36)

Длина стержня l₀ в системе, относительно которой он покоится, больше длины стержня l‘ в системе, относительно которой он движется.

Линейные размеры тела, движущегося относительно инерциальной системы отсчета, уменьшаются в направлении движения в (sqrt {1 — {beta ^2}} ) раз.

Длина отрезка, измеренная в системе отсчёта, в которой он покоится, называется его собственной длиной. Собственная длина всегда имеет наибольшее значение.

Длина отрезка зависит от выбора системы отсчёта, т.е. длина – относительная величина.

В классической механике: (v < < cquad Rightarrow beta = frac{v}{c} < < 1quad Rightarrow l = {l’_0};begin{array}{*{20}{c}}{}end{array}quad l’ = {l_0}.)