Как найти длину стороны аб треугольника абс

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b — катеты, с — гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b — катеты, с — гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b — катеты, с — гипотенуза,α° и β° — углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b — катеты, с — гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a — искомое основание, b — известная боковая сторона,α° — угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a — искомое основание,b — известная боковая сторона,β° — угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b — искомая боковая сторона, a — основание,α° — угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b — искомая боковая сторона, a — основание,β° — угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a — искомая сторона, S — площадь треугольника.

2) Найти сторону через высоту

где a — искомая сторона,h — высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a — искомая сторона,r — радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a — искомая сторона,R — радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a — искомая сторона, b и с — известные стороны, α° — угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a — искомая сторона, b — известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Решение треугольников онлайн С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже. Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это: Три стороны треугольника. Две стороны треугольника и угол между ними. Две стороны и угол противостоящий к одному из этих сторон треугольника. Одна сторона и любые два угла. Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°. Решение треугольника по трем сторонам Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем . (1) (2) Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения . Пример 1. Известны стороны треугольника ABC: Найти (Рис.1). Решение. Из формул (1) и (2) находим: И, наконец, находим угол C: Решение треугольника по двум сторонам и углу между ними Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B. Найдем сторону c используя теорему косинусов: . . Далее, из формулы . . (3) Далее из (3) с помощью калькулятора находим угол A. Поскольку уже нам известны два угла то находим третий: . Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B. Решение. Иcпользуя теорму косинусов найдем сторону c: , Из формулы (3) найдем cosA: . Поскольку уже нам известны два угла то находим третий: Решение треугольника по стороне и любым двум углам Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C. Так как, уже известны два угла, то можно найти третий: . Далее, для находждения сторон b и c воспользуемся тероемой синусов: Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С. Решение. Поскольку известны два угла, то легко можно найти третий угол С: Найдем сторону b. Из теоремы синусов имеем: Найдем сторону с. Из теоремы синусов имеем: источники: http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://matworld.ru/geometry/reshenie-treugolnikov.php

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Пример 1:

Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:

1) уравнения сторон треугольника АВС;

2) координаты точки пересечения медиан;

3) длину и уравнение высоты, опущенной из вершины А;

4) площадь треугольника.

Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан

Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А

Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:

Пример 3:

По координатам вершин треугольника ABC найти:

• периметр треугольника;
• уравнения сторон AB и BC;
• уравнение высоты AD; угол ABC;
• площадь треугольника.

Сделать чертеж.

А(1; 2); В (–1; 2); С(3; 0).

Решение от преподавателя:

Пример 4:

Даны координаты вершин треугольникаА, В, С.

Требуется найти:

1) уравнение и длину стороны ВС;

2) уравнение и длину высоты, проведённой из вершиныА;

3) уравнение медианы, проведённой из вершиныА;

4) площадь треугольника.

Сделать чертёж.

А(4;-3), B(-2;-1), C(3;-2).

Решение от преподавателя:

Пример 5:

Решение от преподавателя:

1)

2)

3) Находим координаты точки М – середины стороны ВС:

       

Определяем длину медианы АМ:

4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору , то составляем уравнение высоты по формуле , где (a,b) – координаты вектора перпендикулярного искомой прямой,  – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:

и подставляем в формулу, ,

6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:

1. Уравнение прямой 
   Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 
   
   Уравнение прямой AB 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-3/₇x + ¹⁶/₇ или 7y + 3x — 16 = 0 
2. Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 
   
   
   M(3;1) 
   Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому: 
   Каноническое уравнение прямой: 
   
   или 
   
   или 
   y = ^-1/₁₁x + ¹⁴/₁₁ или 11y + x — 14 = 0 
3. Уравнение высоты через вершину C 
   Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
   
   Найдем уравнение высоты через вершину C 
   
   y = ⁷/₃x + ⁶²/₃ или 3y -7x — 62 = 0
4. уравнение параллельной прямой AB, проходящей через точку (-8,2)
   Уравнение прямой AB: y = ^-3/₇x + ¹⁶/₇
   Уравнение KN параллельно AB находится по формуле:
   y — y₀ = k(x — x₀)
   Подставляя x₀ = -8, k = ^-3/₇, y₀ = 2 получим:
   y-2 = ^-3/₇(x-(-8))
   или
   y = ^-3/₇x — ¹⁰/₇ или 7y + 3x +10 = 0

Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5). 

Решение от преподавателя:

4) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-1/₄x + ¹⁵/₂ или 4y +x -30 = 0 
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k₁ прямой AB. 
Уравнение AB: y = 4x -3, т.е. k₁ = 4 
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k₁*k = -1. 
Подставляя вместо k₁ угловой коэффициент данной прямой, получим: 
4k = -1, откуда k = ^-1/₄ 
Так как перпендикуляр проходит через точку C(10,5) и имеет k = ^-1/₄,то будем искать его уравнение в виде: y-y₀ = k(x-x₀). 
Подставляя x₀ = 10, k = ^-1/₄, y₀ = 5 получим: 
y-5 = ^-1/₄(x-10) 
или 
y = ^-1/₄x + ¹⁵/₂ или 4y + x — 30 = 0 
Найдем точку пересечения с прямой AB: 
Имеем систему из двух уравнений: 
y -4x +3 = 0 
4y + x — 30 = 0 
Из первого уравнения выражаем y и подставим во второе уравнение. 
Получаем: 
x = ⁴²/₁₇ 
y = ¹¹⁷/₁₇ 
D(⁴²/₁₇;¹¹⁷/₁₇) 
Длина высоты треугольника, проведенной из вершины C 
Расстояние d от точки M₁(x₁;y₁) до прямой Ax + By + С = 0 равно абсолютному значению величины: 

Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника 
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 


Е(7;9) 
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁴/₃x ^-1/₃ или 3y -4x +1 = 0 
Найдем длину медианы. 
Расстояние между двумя точками выражается через координаты формулой: 

6) CD—диаметр окружности. Центр окружности точка О лежит в середине отрезка CD

Уравнение окружности  (x-x₀)²+(y-y₀)²=r²

(x-106/17)²+(y-101/17)²=256/17 

Уравнение прямой, параллельной CD, проходящей через точку A 

Пример 8:

Решение от преподавателя:

Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)

Пример 9:

Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4),  С (-1,6).

Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;

2) периметр (сумму длин) треугольника;

3) уравнение высоты СН;

4) расстояние d от точки С до прямой АВ;

5) сделайте чертеж.

Решение от преподавателя:

Решение.

1) уравнения сторон треугольника АВ, ВС и АС

Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника

Расстояние между двумя точками

3) уравнение высоты СН

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ

Расстояние от точки до прямой

Пример 10:

Даны вершины A (x₁; y₁), B (x₂; y₂), C (x₃; y₃)    треугольника.

Найти: 1) уравнение стороны AB;

2) уравнение медианы, проведенной из вершины C;

3) уравнение высоты, проведенной из вершины C ;

4) уравнение прямой, проходящей через вершину C параллельно стороне AB .

A (6; 0), B (2; − 6), C (−3; −9).

Решение от преподавателя:

Пример 11:

Решение от преподавателя:

Пример 12:

Дан треугольник  с координатами вершин найти:

а) длину стороны AB;

б) косинус угла ABC;

в) площадь треугольника ABC (через векторное произведение);

Решение от преподавателя:

Пример 13:

Решение от преподавателя:

Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9). 
1) Уравнение прямой 
Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂), представляется уравнениями: 

Уравнение прямой AB 
Каноническое уравнение прямой: 

или 

или 
y = ³/₂x -9 или 2y -3x +18 = 0 

2) Уравнение медианы треугольника 
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(4;-3) 
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому: 
Каноническое уравнение прямой: 

или 

или 
y = ⁶/₇x ^-45/₇ или 7y -6x +45 = 0 
3) Уравнение высоты через вершину C 
Прямая, проходящая через точку N₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 

Найдем уравнение высоты через вершину C 

y = ^-2/₃x -11 или 3y +2x + 33 = 0 
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9) 
Уравнение прямой AB: 2y -3x +18 = 0 
Уравнение СN параллельно AB находится по формуле: 

Или     2y -3x +9 = 0 

Пример 14:

Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.

Решение от преподавателя:

Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 


M(-1;0) 
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 

или 

или 
y = ¹/₉x + ¹/₉ или 9y -x — 1 = 0 
3) Уравнение высоты через вершину B

Пример 15:

Дан треугольник АВС. Найти:

а) величину угла А;

б) уравнение стороны АС;

в) уравнение высоты и медианы, опущенных из вершины В.

Сделать чертеж.

А(-1,2); В(1,3); С(3,-4).

Решение от преподавателя:

Пример 16:

Треугольник задан вершинами А(-6; -2);  В(4; 8); С(2; -8). Найти:

а) уравнение прямой BN, параллельной  стороне АС;

б) уравнение медианы CD;

в) уравнение высоты АЕ;

Решение от преподавателя:

а) уравнение прямой BN, параллельной  стороне АС;

Уравнение прямой AC:

Каноническое уравнение прямой:

или

или
y = ^-3/₄x ^-13/₂ или 4y + 3x +26 = 0

Уравнение BN параллельно AC находится по формуле:
y — y₀ = k(x — x₀)
Подставляя x₀ = 4, k = ^-3/₄, y₀ = 8 получим:
y-8 = ^-3/₄(x-4)
или
y = ^-3/₄x + 11 или 4y + 3x — 44 = 0

б) уравнение медианы CD;

Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:

или

или
y = ^-11/₃x ^-2/₃ или 3y + 11x +2 = 0

в) уравнение высоты АЕ;

Прямая, проходящая через точку Е₀(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем уравнение высоты через вершину A

y = ^-1/₈x — ¹¹/₄ или 8y +x + 22 = 0

Пример 17:

A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:

Пример 18:

В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).

Составить уравнения стороны (AB), высоты (ВК)  и медианы (CМ).

Решение от преподавателя:

Уравнение прямой AB
Каноническое уравнение прямой:

или

или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:

или

или
y = ^-1/₄x + 3 или 4y + x — 12 = 0

Найдем уравнение высоты через вершину B

y = 4x + 13 или y -4x — 13 = 0

Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;¹/₂), поэтому:
Каноническое уравнение прямой:

или

или
y = ¹/₂₄x + ²/₃ или 24y -x — 16 = 0

Пример 19:

Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).

Решение от преподавателя:

Треугольником называется фигура, которая состоит их трех точек (вершины), которые не лежат на одной
прямой и трех попарно соединяющих эти точки отрезков (стороны). Треугольники бывают остроугольными,
тупоугольными, прямоугольными, равнобедренными, равносторонними, разносторонними. С данной фигурой
связано много формул, теорем, правил. Ниже приведены формулы и примеры по нахождению стороны
треугольника.

Сторона равностороннего треугольника через радиус описанной окружности

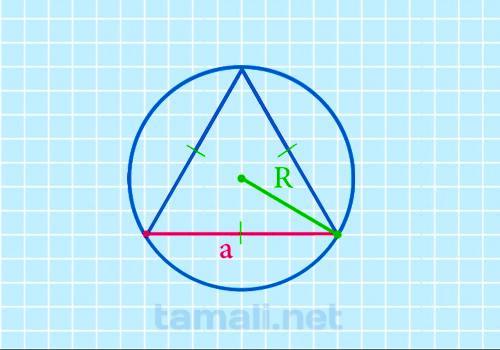
Для того чтобы найти сторону равностороннего треугольника через радиус описанной окружности
необходимо ее радиус умножить на корень квадратный из трех. Таким образом, формула будет выглядеть
следующим образом:

a = R * √3

где а — сторона треугольника, R — радиус описанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом описанной окружности 10см. Подставим в
формулу и получится: a = 10*√3 = 10 * 1,732 ≈ 17,3 см.

Сторона равностороннего треугольника через радиус вписанной окружности

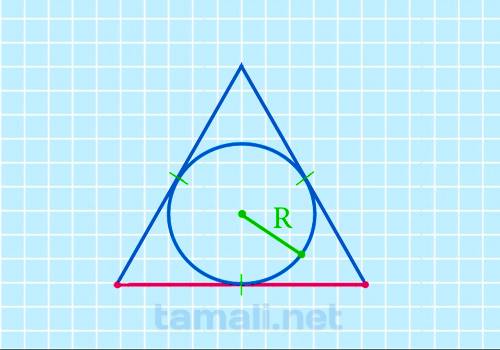
Для нахождения стороны правильного треугольника через радиус вписанной окружности следует
использовать формулу радиуса r= a (√3 / 6). Отсюда можно вывести формулу следующим образом: a = r (6
/ √3) = r *(6√3 / √3√3) = r * (6√3 / 3). Формула будет следующая (удвоенный радиус умножить на
квадратный корень из трех):

a = 2r * √3

где а — сторона треугольника, R — радиус вписанной окружности.

Пример. Пусть дан равносторонний треугольник с радиусом вписанной окружности 23см. Подставим в
формулу и получится: a = 2 * 23 * √3 = 2 * 23 * 1,732 ≈ 79,7см.

Сторона равностороннего треугольника через высоту

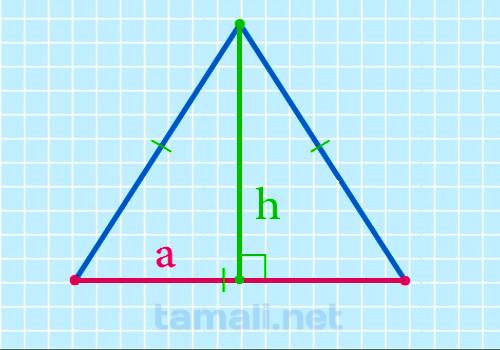
Для того чтобы найти сторону равностороннего треугольника через высоту следует применить теорему
Пифагора. Сторона равностороннего треугольника a² будет равна сумме квадратов высоты и половины
основания, которое также является стороной a: a² = h² + (a/2)² ⇒ a² = h² + a²/4 ⇒ a² — a²/4
=h² ⇒ (4a² — a²) / 4 = h² ⇒ 3a²/4 = h² ⇒ a² = 4*h²/3 ⇒a = √(4h²/3). Отсюда можно вывести
формулу для нахождения стороны через высоту:

a = 2h / √3

где а — сторона, h —  высота равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с высотой 45см. Подставим в формулу и получится: a = 2 *
45 / √3 = 2 * 45 / 1,732 ≈ 51,963 см.

Сторона равностороннего треугольника через площадь

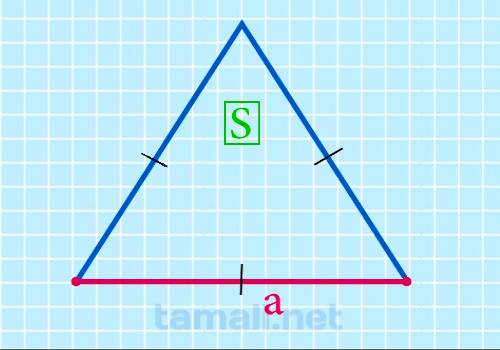
Для того чтобы найти сторону равностороннего треугольника через площадь нужно применить следующую
формулу

a = √(4S / √3)

где а — сторона, S —  площадь равностороннего треугольника.

Пример. Пусть дан равносторонний треугольник с площадью 64м². Подставим в формулу и получится: a =
√(4*64 / √3)= √(4 * 64 / 1,732) ≈ 12,157 см.

Основание равнобедренного треугольника через боковые стороны и угол между ними

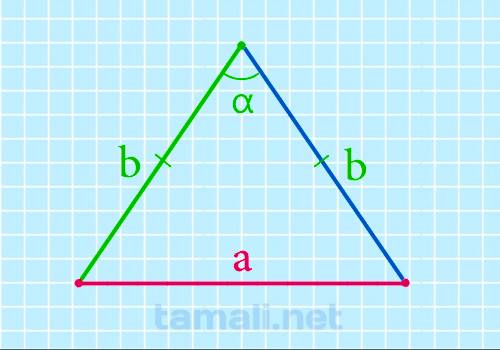
Равнобедренным называется треугольник, у которого есть две равные стороны, называемые ребрами, а
третья сторона основанием. Для того чтобы найти основание нужно знать или один из углов, или высоту
треугольника, приводящаяся к основанию. Его можно вычислить по данной формуле:

a = 2b * sin (α/2)

где a — длина основания треугольника, b — длина стороны треугольника; α — это угол,
который противоположен основанию.

Пример. Если сторона a = 10 см, а ∠β = 12°, то: a = 2⋅10⋅sin 12/2 = 2⋅10⋅0,1045 =2,09 см.

Основание равнобедренного треугольника через боковые стороны и угол при основании

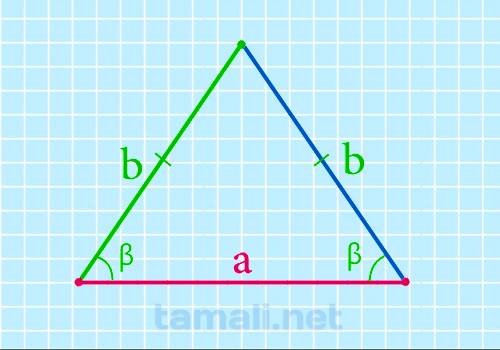
Угол при основании равнобедренного треугольника равен разности 90º и половины угла при его вершине и
чем больше угол при вершине равнобедренного треугольника, тем он меньше. Может быть только острым,
то есть прямым или тупым он быть не может. Если известен угол при основании и боковые стороны, то
можно найти основание равнобедренного треугольника по следующей формуле:

a = 2b + cos β

где b — боковая сторона, β — угол при основании.

Пример. Если сторона a = 10 см, а ∠β = 40°, то: a = 2⋅10⋅cos 40 = 2⋅10⋅0,766 =15.32 см.

Боковая сторона равнобедренного треугольника через основание и угол между боковыми сторонами

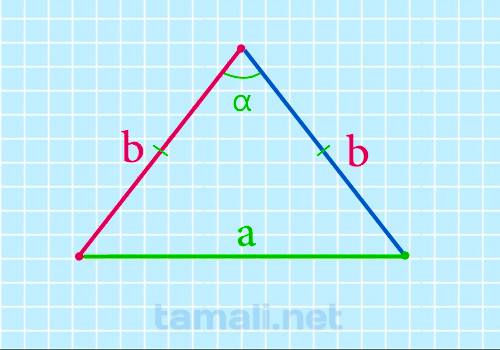
В равнобедренном треугольнике углы при основании (т.е. между боковыми сторонами и основанием) равны,
из чего можно сделать вывод что если углы при основании треугольника одинаковы по значению, значит
он является равнобедренным.  Это значит, что α = β.

Формула, выражающая боковую сторону равнобедренного треугольника через основание и угол боковыми
сторонами:

b = a / (2 * sin(α/2))

где d — основание равнобедренного треугольника, α — угол между боковыми сторонами.

Пример. Если сторона a = 17 см, а ∠α = 50°, то: a = 17 / 2 * sin (50/2) = 17 / 2 * sin 25 = 20.11
см.

Боковая сторона равнобедренного треугольника через основание и угол при основании

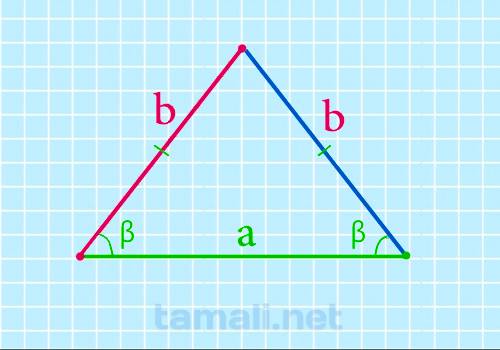
Если известно основание и угол при нем, то формула боковой стороны равнобедренного треугольника будет
выглядеть следующим образом:

b = a / 2 * cos β

где a — это основание, β — угол при основании равнобедренного треугольника.

Здесь длина боковых сторон будет равно b: AB=BC=b, длина основания a: AC=a. Для доказательства
формулы боковой стороны применяется теорема косинусов, вернее, ее следствие.

Пример. Пусть основание (a) равно 35мм, а угол β — 60º, тогда подставив в формулу получим b =
35 / 2 * 0,5=35 мм.

Катет прямоугольного треугольника через гипотенузу и острый угол

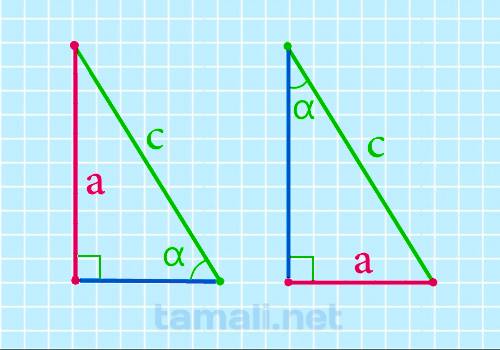
Катет прямоугольного треугольника через гипотенузу и острый угол выражается данным образом: катет,
противолежащий углу α, равен произведению гипотенузы на sin α, то есть формула будет выглядеть
следующим образом:

a = c * sin α

где c — гипотенуза, α — острый угол прямоугольного треугольника.

Пример. Пусть гипотенуза с равна 77см, а острый угол 80º, тогда подставив в формулу значения получим
следующее:  a = 77 * 0,98 = 75,8см.

Катет прямоугольного треугольника через гипотенузу и другой известный катет

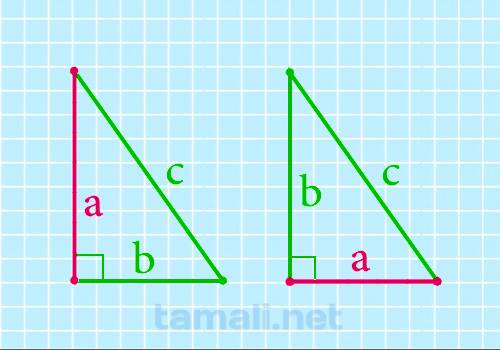
Если известен один катет и гипотенузу, то можно найти другой катет. Для этого необходимо
воспользоваться формулой:

a = √(c² — b²)

где c — гипотенуза, b — катет который известен прямоугольного треугольника.

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а
катет b = 4 см: a = √(5² — 4)² = √(25 — 16) = √9 = 3 см

Гипотенуза прямоугольного треугольника через катет и острый угол

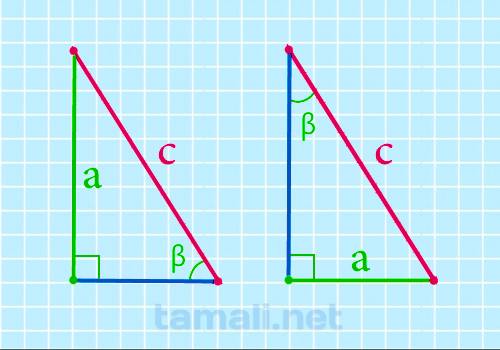
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему
угол можно узнать по формуле:

c = a / sin(β)

где a — катет, β — острый угол прямоугольного треугольника.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 4 см, а
противолежащий к нему ∠β =60°: c = 4 / sin(60) = 4 / 0,87 = 8,04 см.

Гипотенуза прямоугольного треугольника через катеты

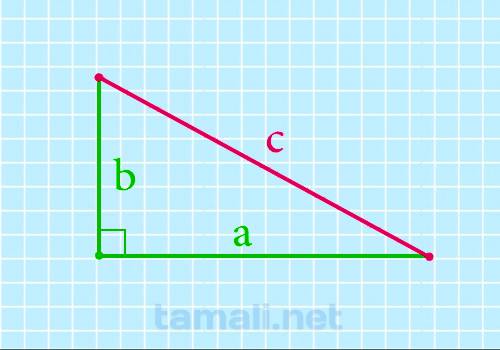
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b) можно рассчитать по
формуле используя теорему Пифагора. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов
катетов: c² = a² + b² следовательно:

c = √(a² + b²)

где c — гипотенуза, a и b — катеты.

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет
b = 4 см: c = √3² + 4² = √9 + 16 = √25 = 5 см

Сторона треугольника через две известные стороны и угол между ними

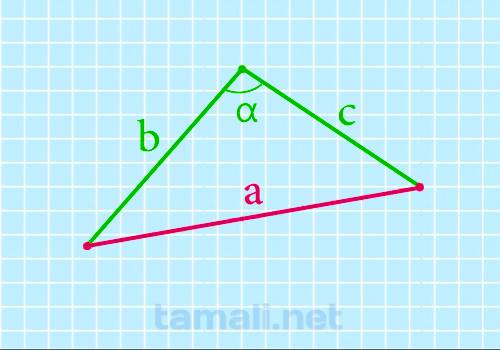
По стороне и двум углам или по двум сторонам и углу можно тоже вычислить длину стороны
треугольника:

a = b² + c² — 2bc * cos α

где a, b, c — стороны произвольного треугольника, α — угол между сторонами который
известен.

Обязательно обратите внимание что при подстановке в формулу, для тупого угла (α>90), cosα
принимает отрицательное значение.

Пример. Пусть сторона с равна 10 см, сторона b — 7, угол α — 60 градусов. Таким образом
получим подставив в формулу:
a = 7² + 10² — 2 * 7 * 10 * cos 60 = 8,89 см.

Сторона треугольника через известную сторону и два угла

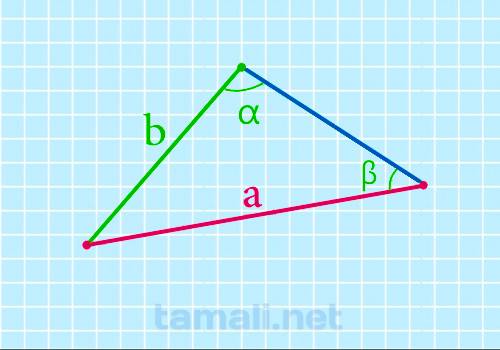
Для нахождения стороны треугольника через известную сторону и два угла необходимо воспользоваться
теоремой синусов и формула будут следующая:

a = (b * sin α) / sin β

где b — сторона треугольника; β, α — углы треугольника.

Пример. Пусть сторона треугольника b равна 10, угол β  = 30º, угол α = 35º. Тогда получим подставив в
формулу следующие значения: Сторона (a) = (10 * sin 35) / sin 30   = 8.71723 мм.