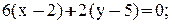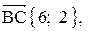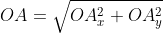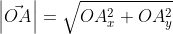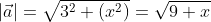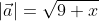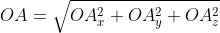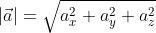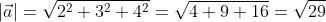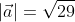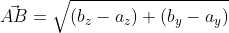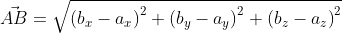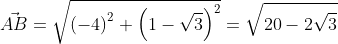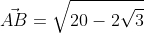Как найти длину стороны если даны точки

Ответ

Проверено экспертом

1)периметр треугольника равен AB + BC + AC. Нам надо найти длину каждой стороны по координатам их концов. Длина отрезка по координатам его концов рассчитывается по формуле

d = √((x2-x1)²+(y2-y1)²), где d — расчитываемый отрезок, x1,x2 — абсциссы начала и конца отрезка, y1,y2 — ординаты начала и конца отрезка.

Подставляя в эту формулу абсциисы и ординаты точек из условия, последовательно нахожу каждую сторону:

Тогда периметр равен √5 + √17 + √10

2)Далее, найду медиану AM. Можно пойти разными путями, но найду её длину методом координат.

Мы знаем, что в этом случае M — середина BC. Нам надо найти координаты точки M, иначе говоря, нам надо найти координаты середины отрезка. Далее, координаты точки A нам известны, значит, можно под первую формулу подогнать. Итак, как же вычислить координаты середины отрезка? Это можно сделать по формуле

x = (x1+x2)/2; y = (y1+y2)/2, где x,y — координаты середины отрезка, x1,x2 — абсциссы концов отрезка, y1,y2 — ординаты концов отрезка. Подставляем исходные координаты в формулу и получаем

x = (3-1)/2 = 2/2 = 1; y = (3+4)/2 = 7/2 = 3.5

Значит, M(1;3.5), A(2;5)

Теперь найдём длину AM по нашей старой формуле:

AM = √(1-2)²+(3.5 — 5)² = √1+2.25 = √3.25

3)Теперь вычислю углы треугольника. Давайте подумаем, как их найти. Я вижу, что нам даны три стороны треугольника(точнее, мы их нашли). Так что, вполне вероятно, что здесь надо воспользоваться теоремой косинусов.(квадрат одной стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними). математически её можно записать так:

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)². В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.

Рассчитаем длину отрезка А, для этого найдем квадратный корень:

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.

Даны координаты вершин треугольника .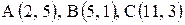

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

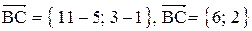
2. Уравнение прямой ВС: ; ; .

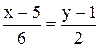
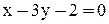
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

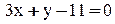
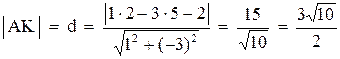
4. Найдем координаты точки N – середины стороны ВС:

; ; .

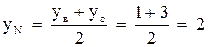
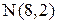
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

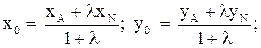
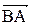
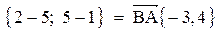
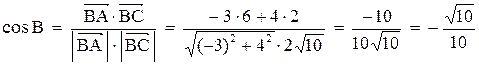
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

.

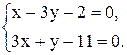
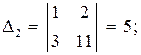
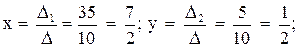
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

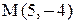
Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	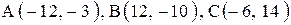.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	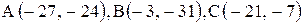.	10.	.
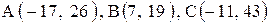11.	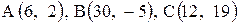.	12.	.
13.	.	14.	.
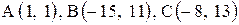15.	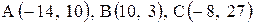.	16.	.
17.	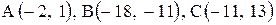.	18.	.
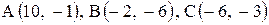19.	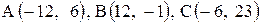.	20.	.
21.	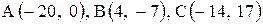.	22.	.
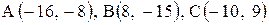23.	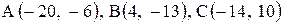.	24.	.
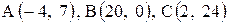25.	.	26.	.
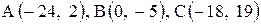27.	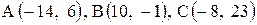.	28.	.
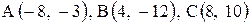29.	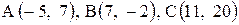.	30.	.

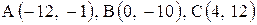Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8447 — | 7339 — или читать все.

Нахождение длины вектора, примеры и решения

Длина вектора — основные формулы

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

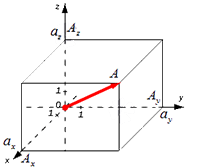
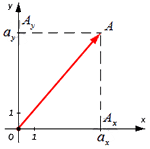
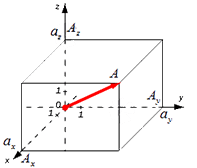
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

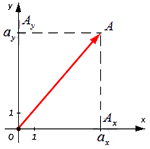
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e

Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.

Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2

А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —

Ответ: A B → = 20 — 2 3 .

Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .

Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :

26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.

Длина вектора — основные формулы

Время чтения: 16 минут

Основные понятия вектора

Для того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.

Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».

Вектор — это отрезок с определённой длиной и направлением.

Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.

Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.

Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.

• Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
• Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.

• Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
• Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.
• Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
  Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.

Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.

Как найти длину вектора

Модуль вектора а будем обозначать .

Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy. Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.

На взятой системе координат, от её начала отложим вектор
В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.

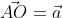
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует

Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора 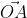получаем

Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:

Когда вектор дан в формате разложения по координатным векторам , то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.

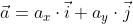
Чтобы рассчитать длину = (3, √x), расположенного в прямоугольной системе координат.

Чтобы найти модуль вектора используем ранее приведённую формулу

Ответ:

Существуют также формулы вычисления длины вектора в пространстве, они выводятся аналогично тем, что в системе координат на плоскости. Если взять вектор =(aₓ ; aᵧ ; a )

В таком случае ( AO^2=OA_x^2+OA_y^2+OA_z^2 ) (из рисунка видно, что АО — диагональ прямоугольного параллелепипеда), поэтому

из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:

Ответ:

Длина вектора через координаты точек начала и конца

Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.

Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле

При этом формула вычисления длины вектора для трёхмерного пространства, с координатами и ), будет следующей:

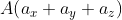
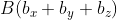
Для прямой системы координат, найти длину вектора ( overrightarrow) , где A(1,√3) B(-3,1)

Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:

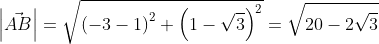
Существует второй вариант решения, где формулы применяются по очереди:

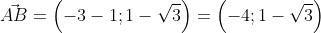
Ответ:

Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,(λ^2))

В первую очередь представим длину вектора в виде формулы.
( left|vecright|=sqrt<left ( b_x-a_x right )^2+ left ( b_y-a_y right )^2 + left ( b_z-a_z right )^2>)
(=sqrt <left ( 5-0 right )^2+ left ( 2-1 right )^2 + left ( lambda^2 -2right )^2>= sqrt<26 + left ( lambda^2 -2right )^2>)
Теперь приравняем полученное выражение к корню из тридцати и найдём неизвестное значение, решив полученное уравнение.
( sqrt<26+left(lambda^2-2right)^2>=sqrt <30>)
( 26+left(lambda^2-2right)^2=30 )
( left(lambda^2-2right)^2=4 )
( lambda^2-2=2 ) или ( lambda^2-2=-2 ) ( lambda_1=-2, lambda_2=2, lambda_3=0. )
Ответ: ( lambda_1=-2, lambda_2=2, lambda_3=0. )

Длина вектора по теореме косинусов

Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.

К примеру, нам известны длины двух векторов (overrightarrow) и (overrightarrow) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора ( overrightarrow ) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.

Даны длины двух векторов ( overrightarrow) и ( overrightarrow) 2 и 4 соответственно, а угол между ними равен ( frac<pi> <3>) . необходимо найти длину ( overrightarrow).

В нашем примере длины векторов и длины сторон треугольника АМК совпадают. Две из сторон нам известны это АК и АМ, а также известен угол треугольника, находящийся между этими сторонами. Используя теорему косинусов получим:
( KM^2=AK^2+AM^2-2cdot AKcdot AMcdotcosfrac<pi><3>)
(=2^2+4^2-2cdot2cdot4cdotcosfrac<pi><3>)
(=4+16-16cosfrac<pi><3>)
(=20-8=12 )
Получается (KM=sqrt <12>)
Ответ: ( left|overrightarrowright|=sqrt <12>)

Теперь мы видим, что для нахождения длины вектора существует несколько формул, которыми можно воспользоваться в зависимости от известных параметров.

длина вектора формула для трёхмерного пространства;

длина вектора формула по известным координатам начала и конца вектора находящегося пространстве; ( left|vecright|=sqrt<left ( b_z-a_z right )^2+ left ( b_y-a_y right )^2>) если известны координаты начала и конца вектора на плоскости.

Существует также формула длины вектора перемещения: ( left|vecright|=sqrt< s_x^2+s_y^2>) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.

В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.

Применение векторов в других сферах

Понятие и вычисление вектора важно не только в математике, но и других науках:

• в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
• в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
• в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
• географии. Вектором обозначается движение воздушных масс, или течение реки;

Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.

Онлайн калькулятор. Модуль вектора. Длина вектора

Этот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал.

Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам

Размерность вектора:

Форма представления вектора:

Инструкция использования калькулятора для вычисления длины вектора

Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел..

Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)

• Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.

Вычисления длины вектора (модуля вектора)

Например, для вектора a = x; a_y; a_z> длина вектора вычисляется cледующим образом:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

источники:

http://www.napishem.ru/spravochnik/matematika/dlina-vektora-osnovnye-formuly.html

http://ru.onlinemschool.com/math/assistance/vector/length/

Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 4 года назад  Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой: Нужно взять лист бумаги в клетку (или даже миллиметровую бумагу) и начертить систему координат. Отмечаем на ней все точки и соединяем их линиями. Затем с помощью линейки измеряем длину каждой линии и складываем все значения. Sadne­ss [5.6K] 4 года назад  Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так: l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере: Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamst­er133­7 [28.6K] 2 года назад  Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стран­е [364K] 3 года назад  Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габба­с [215K] 4 года назад  Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюми­нка [59.9K] 3 года назад  Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп [71.2K] 3 года назад  Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Барха­тные лапки [382K] 3 года назад  Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ?

Как найти длину стороны треугольника

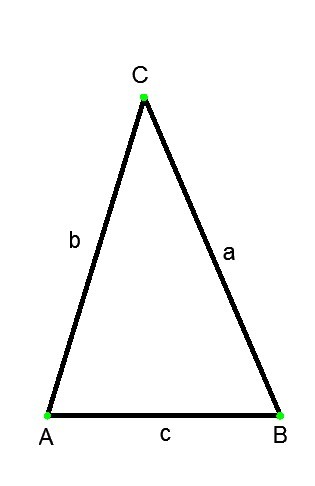
Треугольник – это фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков соединяющих эти точки попарно. Точки называются вершинами (обозначаются заглавными буквами), а отрезки сторонами (обозначаются малыми буквами) треугольника. Различают следующие типы треугольников: остроугольный треугольник (все три угла острые), тупоугольный треугольник (один из углов тупой), прямоугольный треугольник (один из углов прямой), равнобедренный (две его стороны равны), равносторонний (все его стороны равны). Найти сторону треугольника можно разными способами, но это всегда будет зависеть от типа треугольника и исходных данных.

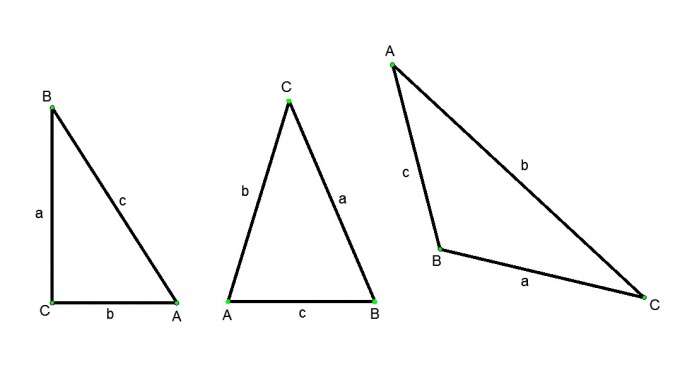
Инструкция

Соотношение сторон и углов в прямоугольном треугольнике:
Пусть ABC – прямоугольный треугольник, угол С – прямой, углы A и B – острые. Тогда согласно определению косинуса: косинус угла A равен отношению прилежащего катета BC к гипотенузе AB. Синусом угла А называется отношение противолежащего катета BC к гипотенузе AB. Тангенсом угла А называется отношение противолежащего катета BC к прилежащему AC.Из данных определений получаем следующие соотношения:
Катет, противолежащий углу А, равен произведению гипотенузы на синус А, или равен произведению второго катета на тангенс А;
Катет, прилежащий к углу А, равен произведению гипотенузы на косинус А;
В прямоугольном треугольнике любая из сторон может быть вычислена по теореме Пифагора, если известны две другие. Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

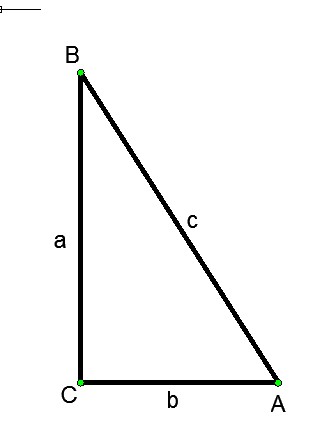
Соотношение сторон в произвольном треугольнике:
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?