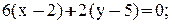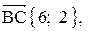Как найти длину стороны если известны координаты

Ответ

Проверено экспертом

1)периметр треугольника равен AB + BC + AC. Нам надо найти длину каждой стороны по координатам их концов. Длина отрезка по координатам его концов рассчитывается по формуле

d = √((x2-x1)²+(y2-y1)²), где d — расчитываемый отрезок, x1,x2 — абсциссы начала и конца отрезка, y1,y2 — ординаты начала и конца отрезка.

Подставляя в эту формулу абсциисы и ординаты точек из условия, последовательно нахожу каждую сторону:

Тогда периметр равен √5 + √17 + √10

2)Далее, найду медиану AM. Можно пойти разными путями, но найду её длину методом координат.

Мы знаем, что в этом случае M — середина BC. Нам надо найти координаты точки M, иначе говоря, нам надо найти координаты середины отрезка. Далее, координаты точки A нам известны, значит, можно под первую формулу подогнать. Итак, как же вычислить координаты середины отрезка? Это можно сделать по формуле

x = (x1+x2)/2; y = (y1+y2)/2, где x,y — координаты середины отрезка, x1,x2 — абсциссы концов отрезка, y1,y2 — ординаты концов отрезка. Подставляем исходные координаты в формулу и получаем

x = (3-1)/2 = 2/2 = 1; y = (3+4)/2 = 7/2 = 3.5

Значит, M(1;3.5), A(2;5)

Теперь найдём длину AM по нашей старой формуле:

AM = √(1-2)²+(3.5 — 5)² = √1+2.25 = √3.25

3)Теперь вычислю углы треугольника. Давайте подумаем, как их найти. Я вижу, что нам даны три стороны треугольника(точнее, мы их нашли). Так что, вполне вероятно, что здесь надо воспользоваться теоремой косинусов.(квадрат одной стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними). математически её можно записать так:

Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.

Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.

Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 — y1)² + (x2 — x1)². В данном случае |AB| является длиной отрезка.

Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 — 1)² + (5 — 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.

Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.

Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.

Рассчитаем длину отрезка А, для этого найдем квадратный корень:

Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.

Даны координаты вершин треугольника .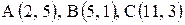

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

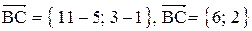
2. Уравнение прямой ВС: ; ; .

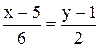
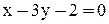
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

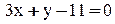
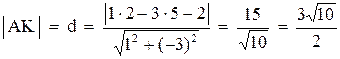
4. Найдем координаты точки N – середины стороны ВС:

; ; .

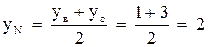
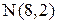
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

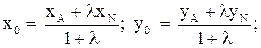
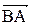
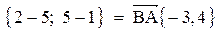
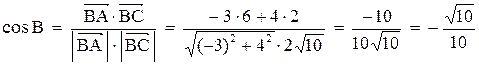
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

.

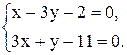
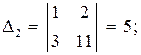
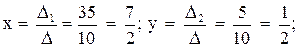
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

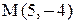
Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	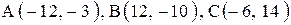.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	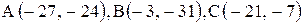.	10.	.
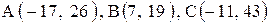11.	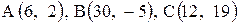.	12.	.
13.	.	14.	.
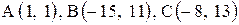15.	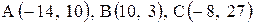.	16.	.
17.	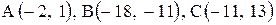.	18.	.
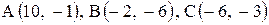19.	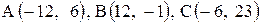.	20.	.
21.	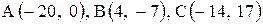.	22.	.
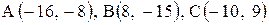23.	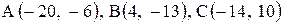.	24.	.
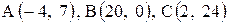25.	.	26.	.
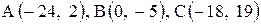27.	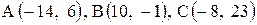.	28.	.
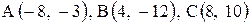29.	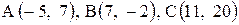.	30.	.

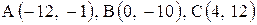Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8447 — | 7339 — или читать все.

Нахождение длины вектора, примеры и решения

Длина вектора — основные формулы

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

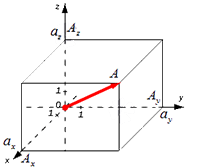
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

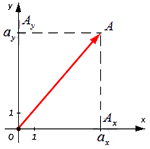
От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e

Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.

Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2

А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —

Ответ: A B → = 20 — 2 3 .

Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .

Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :

26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Площадь треугольника по координатам вершин — формулы для расчета

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

1. Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.
2. Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

Тогда координаты его векторов AB- и AC- выразятся так:

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

1. Необходимо определить координаты векторов, образующих стороны треугольника.
2. Затем, следует вычислить длины их сторон.
3. Посчитать полупериметр фигуры.
4. Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

1. Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.
2. Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

Площадь треугольника по координатам вершин — формулы для расчета

Использование координатной плоскости в математике является удобным изобретением для расчета различных геометрических характеристик фигур. Одной из них является площадь треугольника. По координатам вершин фигуры это свойство можно рассчитать несколькими различными способами.

Самый простой многоугольник и вектор

Чтобы найти площадь треугольника через векторы и известные координаты его вершин, необходимо подробнее познакомиться с этими геометрическими объектами. Знание их свойств позволяет легко вычислять разные характеристики изучаемой фигуры, включая периметр, высоту, углы при вершинах и другие. При этом используются универсальные математические операции, которые можно применять с успехом не только для треугольника, но и для других многоугольников.

Фигура на плоскости

Треугольник в геометрии представляет собой самый простой многоугольник, который лежит всегда в одной плоскости, даже если фигура рассматривается в трехмерном пространстве. Состоит он из сторон и вершины.

Сторон и вершин у фигуры по три. Сторона является отрезком, а вершина — это точка пересечения этих отрезков. Для нее характерен определенный угол. Все углы треугольника являются разными в общем случае, их сумма всегда соответствует 180°. Однако, существуют специальные типы фигуры, для которых либо два угла равны друг другу (равнобедренный), либо все три (равносторонний). В задачах называют треугольники по имени их трех вершин, обозначенных латинскими буквами, например, ABC или NPQ.

Для треугольника важное значение имеют следующие отрезки:

• делящий противоположную углу сторону пополам — медиана;
• разделяющий угол при вершине на два равных — биссектриса;
• падающий под прямым углом на противоположную углу сторону — высота.

Высота, например, используется для расчета площади фигуры. Для равностороннего треугольника все эти отрезки совпадают друг с другом для любой вершины, а для равнобедренного они одинаковы лишь для угла, образованного равными сторонами.

Направленный отрезок

Вектором называют линейный элемент, который имеет начало и конец. Для его определения удобнее всего использовать координатную плоскость. Она представляет собой две направленные оси, имеющие шкалу и пересекающиеся под углом 90°. Точка пересечения является началом координат и обозначается буквой O (0; 0). Здесь каждая из цифр указывает точку пересечение перпендикуляра, опущенного из рассматриваемого объекта к каждой из двух осей.

Если начало A (x0; y0) и конец B (x1; y1) вектора известны, тогда легко можно вычислить его собственные координаты. Делается это так:

AB- = B-A = (x1-x0; y1-y0).

Иными словами, чтобы получить вектор AB-, следует из соответствующих координат его конца вычесть его начало. Эта операция эквивалентна параллельному перемещению AB- в начало координатной плоскости, что говорит о существовании бесконечного количества одинаковых AB-векторов.

Направленные отрезки можно складывать, вычитать и умножать. Для каждой из операций существуют определенные правила. Если для сложения и вычитания речь идет о геометрических особенностях, то в случае умножения применяются исключительно алгебраические выражения. Вектор a- можно умножить на b- двумя принципиально разными способами:

Скалярно: (a-*b-). В этом случае мы получаем число. Правило умножения записывается следующим образом: (a-*b-) = |a-|*|b-|*cos (ab)=x1*x2+y1*y2. Здесь знаком модуля (||) обозначены длины соответствующих отрезков, cos (ab) — это косинус угла между a- и b-, при этом a-(x1; y1), b-(x2; y2). Этот тип произведения можно использовать для вычисления углов между направленными отрезками, а также для определения объема фигур в пространстве.

Векторно: [a-*b-]. Результатом этой операции является вектор, который перпендикулярен исходным, его направление (вверх или вниз) принято определять по правилу правой руки: четыре пальца должны быть направлены от конца a- к концу b-, тогда оттопыренный большой палец укажет направление их векторного произведения. Длина этого перпендикулярного вектора определяется так: [a-*b-] = |a-|*|b-|*sin (ab) = x1*y2-x2*y1. Векторное произведение используют для вычисления площадей фигур.

Методы вычисления площади по координатам

Задачи на вычисление площадей, периметров или объемов фигур по известным координатам их вершин являются типичными для школьного курса геометрии. В связи с развитием современных технологий школьники часто ищут в интернете, как решить треугольник онлайн по координатам. Тем не менее, существует ряд простых способов, которые позволяют быстро найти площадь фигуры, если известно расположение трех его вершин на координатной плоскости.

Универсальный подход

Этот метод можно применять всегда, независимо от того, какой тип треугольника рассматривается. Известно, что площадь фигуры вычисляется, как произведение половины стороны на опущенную на нее высоту: S = ½*a*h.

Пусть имеются координаты вершин заданного треугольника ABC:

Тогда координаты его векторов AB- и AC- выразятся так:

Если провести высоту h треугольника ABC к любой из этих сторон, например, к AC, то ее длина может быть рассчитана с использованием тригонометрической функции синуса:

Здесь α является углом между векторами-сторонами AB- и AC-. Тогда формулу площади можно переписать в следующем виде: S = ½*a*h = ½*AC* AB*sin (α).

Можно заметить, что записанное выражение является не чем иным, как векторным произведением для AB- и AC-, поэтому можно переписать формулу для S так:

S = ½*[ AB-* AC- ] = ½*((x2-x1)*(y3-y1) — (y2-y1)*(x3-x1)).

Можно аналогично показать, что подобные выражения получаются для пар векторов AC-, BC- и AB-, BC-.

Рекомендуется не запоминать конечные выражения для площади треугольника, поскольку они являются несколько громоздкими, и при их использовании ученики могут запутаться. Для решения подобного рода задач достаточно понять свойства векторов и единственную универсальную формулу для S для любого типа треугольников.

Любопытно отметить, что векторное произведение при вычислении площади можно применять не только для треугольников, но и для любых четырехугольников. Так, в случае параллелограмма рассматриваемая характеристика будет точно равна векторному произведению любых смежных (непараллельных) его сторон.

Использование формулы Герона

Этот способ также может считаться универсальным, поскольку он применим к любым типам треугольников. В работе Герона Александрийского, которая называется «Метрика» и относится к I веку нашей эры, впервые было обнаружено выражение, позволяющее по длинам сторон рассматриваемой фигуры определить ее площадь. Формула имеет следующий вид:

Здесь p — полупериметр, a, b, c — длины сторон.

Последовательность этапов решения задачи можно выразить таким образом:

Необходимо определить координаты векторов, образующих стороны треугольника.

Затем, следует вычислить длины их сторон.

Посчитать полупериметр фигуры.

Применить формулу Герона.

Ключевым этапом является определение длины вектора. Пусть AB- имеет координаты (x1; y1), тогда его длина вычисляется так:

|AB-| = (x1 2 + y1 2 )^0,5.

Длина любого вектора как на плоскости, так и в пространстве, вычисляется, как сумма квадратов всех его координат, взятых под корень.

Очевидно, что можно записать общее выражение для площади треугольника через координаты с использованием формулы Герона, но оно будет слишком громоздким, поэтому нет никакого смысла запоминать его.

Другие способы

Существуют эмпирические правила, которые можно запомнить и легко решать задачи на определение площади треугольника. Пусть координаты его вершин задаются так: A (x1; y1), B (x2; y2), C (x3; y3). Предположим, что порядок вершин A, B, C расположен против часовой стрелки, тогда существуют следующие правила определения площади ABC:

Можно воспользоваться формулой: S = ½*(x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)). То есть выбирается первая координата вершины и умножается на разность вторых координат двух других вершин, возникающих против хода стрелки часов от первой. Затем, все три члена складываются и делятся на 2.

Матричный способ. Необходимо выписать в столбик пары координат каждой вершины против часовой стрелки и завершить координатами исходной. После этого следует сложить три попарных произведения первой и второй координат двух соседних вершин, а затем, вычесть три попарных произведений второй и первой координат тех же вершин. Результат поделить пополам. Например: (x1; y1) (x2; y2) (x3; y3) (x1; y1). S = ½*(x1*y2 + x2*y3 + x3*y1 — y1*x2 — y2*x3 — y3*x1).

Решение задачи

Дана фигура АВС. Найдите площадь треугольника, вершины которого имеют координаты A (1; -3), B (2; 5), C (-2; -2).

Для нахождения решения следует обратиться за помощью к универсальному способу. Сначала необходимо выбрать два вектора, образующих стороны треугольника. Пусть это будут AB- и BC-. Теперь нужно знать их координаты. Они равны:

Чтобы рассчитать площадь, достаточно вычислить полупроизведение векторное для выбранных направленных отрезков: S = ½*[AB-*BC-] = ½*(1*(-7)-8*(-4)) = 12,5 квадратных единиц.

Таким образом, существует несколько методик вычисления площади треугольника, если известны координаты его вершин. Все они сводятся к использованию свойств векторов и известных формул. Существуют также выражения, которые следует запомнить, чтобы решать подобные задачи.

источники:

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://b4.cooksy.ru/articles/koordinaty-vershin-treugolnika-vektory

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Координаты вершин треугольника векторы Решить треугольник Онлайн по координатам 1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис; 2) система линейных неравенств, определяющих треугольник; 2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам; 3) внутренние углы по теореме косинусов; 4) площадь треугольника; 5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами; 10) параметры вписанной и описанной окружностей и их уравнения. Внимание! Этот сервис не работает в браузере IE (Internet Explorer). Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Как находить периметр геометрических фигур (треугольник, четырёхугольник, многоугольник) по известным координатам вершин? Какая формула должна использоваться? Формула для вычисления длины стороны АВ по известным координатам: Аналогичным образом высчитываются остальные стороны, а затем полученные величины суммируются. автор вопроса выбрал этот ответ лучшим Ксарф­акс [156K] 4 года назад  Периметр по координатам Периметр фигуры — это сумма длин всех её сторон. Чтобы в нашем случае найти длины сторон, нужно воспользоваться формулой длины отрезка по заданным координатам (x1; y1) и (x2; y2): Последовательно складываем все полученные значения и получаем периметр. Если в задаче вид фигуры (квадрат, прямоугольник, равносторонний треугольник и т.п.) оговаривается заранее, то находить все длины может и не понадобиться. Например, периметр квадрата ABCD будет равен 4 * AB, так как у этой фигуры все стороны равны. То есть будет достаточно вычислить, чему равна сторона AB и умножить её на 4. Рассмотрим несколько примеров. 1) Треугольник ABC имеет координаты A(1,1); B(1,3); C(2,1). P(ABC) = AB + AC + BC. AB = √(0 + 2²) = √4 = 2. AC = √(1² + 0) = √1 = 1. BC = √(1² + (-2)²) = √5 ≈ 2,24. Таким образом, P(ABC) ≈ 2 + 1 + 2,24 = 5,24. 2) Прямоугольник ABCD имеет координаты A(2,1); B(2,4); C(3,4); C(3,1). P(ABCD) = 2AB + 2BC (так как по определению прямоугольника AB = CD и BC = AD). AB = √(0 + 3²) = √9 = 3. AC = √(1² + 0) = √1 = 1. Таким образом, P(ABC) = 3 * 2 + 1 * 2 = 8. ** Найти периметр по координатам можно и без использования формулы длины отрезка. Порядок действий такой: Нужно взять лист бумаги в клетку (или даже миллиметровую бумагу) и начертить систему координат. Отмечаем на ней все точки и соединяем их линиями. Затем с помощью линейки измеряем длину каждой линии и складываем все значения. Sadne­ss [5.6K] 4 года назад  Так как координаты вершин нам известны, то, для нахождения периметра, остаётся просто вычислить длину каждой стороны и сложить их. Длина отрезка вычисляется так: l=sqrt((x2 — x1)^2 + (y2 — y1)^2); Важно: вычитаем всегда начало из конца. Нахождение на примере: Найдём длины всех трёх сторон и сложим. AB=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((12 — 1)^2 + ((-5) — 8)^2)=sqrt(121 + 169)=sqrt(290); BC=sqrt((x2 — x1)^2 + (y2 — y1)^2)=sqrt((-2 — 12)^2 + (1 — -(5))^2)=sqrt(196 + 36)=sqrt(232); CA=sqrt((1 — (-2))^2 + (8 — 1)^2)=sqrt(9 + 49)=sqrt(58); Далее просто складываем полученные результаты: P=AB+BC+CA; Ну вот и всё, так просто находится периметр по заданным координатам(для любой фигуры). P.s извиняюсь за плохо подобранные координаты. Давайте сначала вспомним, что такое периметр фигуры и как его вычислить. Периметром называется сумма длин всех сторон данной фигуры. Таким образом, для вычисления периметра какой-либо фигуры нужно знать длину всех ее сторон. Затем дело останется за малым — просто сложить длины. По сути, сторона любого многоугольника ( треугольника, четырехугольника, пятиугольника и так далее ) представляется собой отрезок. Для вычисления длины отрезка по координатом его концов используется следующая формула: , где х1 и х2 — координаты концов отрезка по оси х, а y1 и y2 — координаты по оси у. Подставляем в формулу значения, проводим вычисления. Находим длину каждой из сторон. Суммируем все длины. Hamst­er133­7 [28.6K] 2 года назад  Периметр геометрических фигур по координатам вершин можно найти при помощи формулы Где x1,x2 это первая координата, y1,y2 это вторая координата. Данную формулу нужно применять к каждой паре соседних вершин многоугольника. После обхода и суммирования всех длин будет получен периметр. Алиса в Стран­е [364K] 3 года назад  Любая геометрическая фигура это совокупность отрезков, составляющих ее стороны, и вершин а ее периметр — сумма длин этих отрезков, сумма сторон, поэтому если мы найдем длины всех сторон и сложим их, то получим как раз периметр фигуры. Для того, чтобы найти длину отрезка АВ, зная его координаты, есть такая вот формула: где точка А имеет координаты (x1; y1), а точка В — координаты (x2; y2). Итак, длину отрезка мы находить научились. Допустим теперь, что у нас есть треугольник АВС, мы знаем координаты его вершин, по указанной выше формуле мы находим длины отрезков АВ, ВС, АС и складываем их, получая периметр этого треугольника АВС: АВ + ВС + АС. габба­с [215K] 4 года назад  Периметр любого многоугольника вычисляется как сумма длин всех его сторон. Значит задача сводится к нахождению длины отрезка по координатам его концов. А это известная формула из курса геометрии основной школы. Итак, длина отрезка d = sqrt(x2^2 — x1^2) + (y2^2 — y1^2), х1 и у1 координаты начала, х2,у2 — координаты конца отрезка. Таким образом находим длины всех сторон многоугольника и суммируем эти значения. Лара Изюми­нка [59.9K] 3 года назад  Во-первых, вспомним, что такое периметр — это сумма длин сторон. То есть нам нужны длины сторон многоугольника. Чтобы их найти, зная координаты точек, воспользуемся формулой из геометрии для нахождения расстояния между двумя точками на плоскости: AB = √(xb — xa)2 + (yb — ya)2. То есть нужно вычислить корень квадратный из суммы квадратов разницы координат по х и по у. Если фигура в пространстве, то добавится еще разница координат по z. AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2 Когда длины всех отрезков найдем остается их только сложить. Периметром фигуры зовется сумма длин всех сторон. Для поиска длинны сторон воспользуйтесь формулой длинны отрезка согласно координатам, которые заданы. (x1; y1) и (x2; y2): Так, если вы последовательно сложите значения, которые получите, то сможете получить периметр. Что касается примеров, при условии наличия координат по точкам А (4;2), В(-6;-3), С(0;8) Следует сложить — получить. Бекки Шарп [71.2K] 3 года назад  Если геометрическая фигура находится в системе координат и координаты ее вершин известны, то длину сторон будем искать по такой формуле: У нас есть треугольник. Координаты его точек- А (4;2), В(-6;-3), С(0;8) Находим длины отрезков АВ, ВС и АС по формуле. Складываем полученные результаты и получаем периметр. Барха­тные лапки [382K] 3 года назад  Существует формула, по которой можно вычислить длину отрезка, если известны координаты. Делим нашу геометрическую фигуру на отрезки, считаем длину каждого отрезка и затем все значения длин складываем. Таким образом мы получаем периметр. Знаете ответ?