Как найти длину тела в физике - Исправление недочетов и поиск решений вместе с Examum.ru

Физика > Длина

Длина в физике – физическая мера. Узнайте, как обозначается длина в физике, формула, как найти длину, какой буквой делают обозначение, единица измерения.

Длина отображает физическое измерение дистанции, которая в системе единиц отображена в метрах.

Задача обучения

Различать СИ (система единиц) и обычные единицы длины.

Основные пункты

Единицей СИ выступает метр.
Один метр – дистанция, которую свет преодолевает в вакууме за 1/299 792 458 секунды.
Единицы на счетчике разработаны вокруг числа 10.

Термин

Длина – физическая удаленность между объектами.

Давайте разберемся в том, что собою представляет длина в физике. Длина – измерение физической дистанции. Многие характеристики наблюдения строятся на определении длины. От нее зависит дистанция между объектами, степень силы, оказываемая объектом, и скорость перемещения. Чтобы точно описать длину, необходимо полагаться на общепринятую единицу измерения в физике.

Известно, что в различных частях мира используют разные единицы измерения длины (например, в США – дюйм). Обычно, если речь идет о региональном масштабе, то проблем не возникает. Но при сотрудничестве между странами появляются нестыковки. Именно поэтому возникла необходимость в стандартной единице измерения, принятой на международном уровне. Таким образом, выбор пал на метр, потому что он лучше всего сотрудничает со скоростью света.

Один метр вычисляет дистанцию, которую свет преодолевает за 1/299 792 458 секунды. Все показатели основываются на счетчике с кратностью в 10. Например, 1 км = 1000 м.

Источник

Большая L и маленькая l в физике — в чем разница, это одно и то же?

Не только в физике, но и в математике, геометрии буква «l» употребляется для обозначения длины. Например, формула длины окружности круга выглядит так:

l=2πr

формула сопротивления проводника длиной l и сечением S:

R=ρl/S

Большая буква «L» используется для обозначения индуктивности проводника, измеряется в Гн (Генри). L — это коэффициент пропорциональности между величиной магнитного поля (Ф) и длиной проводника (l).

Таким образом в формуле Ф = L*l присутствуют обе рассматриваемые буквы.

автор вопроса выбрал этот ответ лучшим

bull-shit
[23.6K]

более месяца назад

L (если она будет заглавная) в физике, не что иное, как индуктивность. Что это? В цепи (электрической) присутствует элемент, который энергию будет накапливать, от поля магнитного, либо это поле он трансформирует в иной вид энергии. Пример — катушка. А вот l, это не что иное как длина на этой катушке намотки, но может быть и сила самого тока. Как найти L?

Iphone-2023
[5.6K]

3 месяца назад

Парообразования теплота — есть в физике такое вот понятие, которое показывает сколько же теплоты (какое количество) потребуется для некоего вещества, при этом давление/температура неизменны, чтобы оно поменяло свое агрегатное состояние, то есть из жидкости, которой оно было до того, стало паром. L будет равно потраченной теплоте, которая делится на массу.

LionBlue
[44.1K]

более года назад

Чтобы ответить на представленный вопрос, нужно знать обозначения единиц в физике. Итак:

I может обозначать как силу тока, которая измеряется в такой величине как ампер и показывает заряд (протекающий) за какое-то время, так и объект в измерении пространственном, его протяженность, соответственно, измеряемую в метрах. Также это показатель у вращающегося объекта момента инерции;
L может показывать, с каким импульсом объект вращается, то есть это момент импульса (килограмм на метр квадратный), а может быть размерностью пространственных величин.

К вопросу подходит формула, определяющая индуктивность проводника:

L-это удельная теплота парообразования.Её единица-джоуль:кг.L=Q:m (L=количество теплоты:массу)

Знаете ответ?

Источник

Как найти длину формулы по физике?

При движении без ускорения путь равен произведению скорости на расстояние: S = v ⋅ ( t 2 − t 1 ) = v ⋅ Δ t , где – скорость тела, — момент времени окончания движения, — момент времени начала движения, — время движения.

Как найти а в физике формула?

A = Fs, где А — работа, F — сила и s — пройденный путь. За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.

Как будет ширина по физике?

Для обозначений могут быть использованы и соответствующие заглавные буквы, в литературе часто встречается сочетание L, B, H (L – длина, В – ширина, Н — высота). Эти же буквы приняты и в физике для обозначения длины, ширины, высоты объектов.

Как понять где длина и ширина?

Длина всегда представляет собой направление наибольшего размера. Ширина – это протяженность между двумя точками плоскости, которые лежат, в отличие от длины, на наименьшем расстоянии друг от друга. То есть, длина – это наибольший размер предмета, а ширина – наименьшей.

Как найти L по физике?

Формула:T = 2π√L/g.

Как найти R по физике?

Соотношения закона Ома

U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
I = U / R.
> U пит (иногда также обозначается как V или Е): напряжение питания. …
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. …
>

Как найти полезную работу в физике формула?

Решение. Полезная работа в рассматриваемой задаче равна работе по подъему тела на высоту h груза массы m, это работа по преодолению силы тяжести. Она равна: Ap=mgh (1.1).

Как вычислить длину круга?

Длина окружности круга равна двум пи умноженным на радиус. — это формула, которая помогает высчитывать точный периметр круга.

Как найти длину прямоугольника 5 класс?

Чтобы найти длину прямоугольника, надо его площадь разделить на ширину. 8.1)Запиши формулы периметра и площади квадрата со стороной b см.

Как обозначаются размеры в физике?

В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Источник

Обновлено: 27.05.2023

Длина́ — физическая величина, числовая характеристика протяжённости линий.

В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.

В узком смысле под длиной понимают линейный размер предмета в продольном направлении(это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).

1. Протяжение линии, плоскости, тела в том направлении, в котором две крайние его точки наиболее удалены друг от друга. Меры длины. Измерить длину и ширину. || Расстояние между концами чего-л.; протяжение, протяженность. Длина отрезка прямой. Длина пути. Длина судоходного канала. □ Веревка была длиною почти во всю комнату. Пушкин, Дубровский. На окраине [города], по всей длине улицы, остановилась на ночь колонна грузовых машин. Первенцев, Огненная земля.

2. Продолжительность, длительность. Длина рабочего дня. Длина рассказа.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).

от англ. length (длина).

ДЛИНА’, ы́, мн. нет, ж. Протяжение линии, плоскости, тела в том направлении, в к-ром две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Д. стола. Меры длины (совокупность принятых единиц линейного измерения). || Протяжение пути вдоль чего-н. Д. окружности. Д. реки. Д. дороги. || перен. Длительность, величина. Д. романа.

длина́

Длина – одна из базовых характеристик измерения объекта в физике.

Задача обучения

Основные пункты

Длина выступает мерой наиболее длинного измерения тела.
Деформация – изменение длины.
Единица измерения – метр.

Термины

Специальная теория относительности: примиряет принцип относительности с отсылкой на то, что скорость света остается постоянной во всех системах отсчета.
Измерение – мера пространственной протяжности в конкретном направлении (высота, ширина, глубина, длина).

Длина

Длина в физике отображает собою одну из характеристик объекта. Причем этим понятием широко пользуются в бытовом смысле. Например, можно отрезать определенную длину провода. Она способна отличаться от высоты (вертикальная протяжность) или ширины (расстояние между сторонами).

Длина выступает мерой одного измерения, площадь – двух (квадрат длины), а объем – трех. Из-за специальной теории относительности длину не считают постоянной во всех системах отсчета. Поэтому, ваша метровая линейка не будет отображать одно значение. Оно меняется в зависимости от наблюдателя.

Единицы

Какая единица длины в физике? Одна из старейших величин – локоть (от кончика пальца до локтя). Дальше ее делили на ногу, руку или палец. Могли также увеличить – шаг. Однако подобные единицы не стабильны, ведь величина локтя меняется в зависимости от человека.

В физике длина стала синонимом для дистанции. Единицы могут основываться на частях тела или пройденном расстоянии между определенными точками. Официальной выступает метр и определяется в соотношении со скоростью света. Также применяют сантиметры и километры. В английской системе – дюйм, фут, ярд и миля. Когда речь идет о космических дистанциях, то используют световой год и парсек.

Морские волны — далеко не все примеры волн. И длина волны — это не серферская характеристика, а вполне себе физическая величина. Сегодня разберемся, что такое волна и как ее охарактеризовать.

О чем эта статья:

Волна: продольная и поперечная

Начнем с того, что волна — это распространение колебания в пространстве.

Волны бывают механическими и электромагнитными.

Механические волны — это те волны, колебания которых можно почувствовать физически, потому что они распространяются в упругой среде.

Например, звук. Когда звук распространяется внутри какого-либо вещества, мы можем ощутить его прикосновением.

Представьте, что вы стоите на железнодорожных путях. Нет, вы не Анна Каренина, вы — экспериментатор.

Если к вам приближается поезд, вы рано или поздно его услышите. Вернее, услышите, как только звуковая волна со скоростью 𝑣 = 330 м/с достигнет ваших ушей.

Если приложить ухо к рельсу, то это произойдет значительно быстрее, потому что скорость звука в твердом теле больше, чем в воздухе. Кстати, под водой скорость звука больше, чем в воздухе, но меньше, чем в твердых телах.

Если вы когда-нибудь трогали музыкальную колонку, то знаете, что звук чувствуется и на ощупь.

Электромагнитные волны — это те волны, которые мы потрогать не можем.

Для них работают все те же самые законы, просто их скорость значительно больше и равна скорости света c = 3 · 10 8 м/с. И источники у них разные.

Волны также принято делить на продольные и поперечные:

Продольные — это те волны, у которых колебание происходит вдоль направления распространения волны.

Дрожание окон во время грома или сейсмические волны (землетрясения) — это пример продольных волн.

Поперечные — волны, у которых колебание происходит поперек направления распространения волны.

Представьте, что вы запустили волну из людей на стадионе — она будет поперечной.
Видимый свет и дрожание гитарной струны — тоже поперечные волны.

На самом деле в ней есть и продольная, и поперечная составляющие, поэтому ее нельзя отнести к конкретному типу.

Длина волны: определение и расчет

Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.

Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.

Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.

Формула периода колебания волны

T = t/N

N — количество колебаний [—]

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Связь со скоростью

Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).

Формула скорости

𝑣 = S/t

Переходя к волнам, можно провести следующие аналогии:

А для скорости даже аналогия не нужна — скорость и в Африке скорость.

Формула скорости волны

𝑣 = λ/T

λ — длина волны [м]

Задачка

Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?

Решение:

Резонанс

Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.

На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.

Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.

Формула частоты

ν = N/t

N — количество колебаний [—]

В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст🙂

Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.

В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.

Читайте также:

Как получают ртуть кратко

Особенности игровой деятельности детей с дцп кратко

Как вырабатывают пористый шоколад кратко

Аспекты целостного педагогического процесса высшей школы

Проблема истины в философии практика как критерий истины кратко

Источник

Главная >> В мире больших скоростей >> Специальная теория относительности

Займемся теперь проблемой измерения длины. Здесь нам также придется встретиться с некоторыми неожиданностями.

Представим себе, что нам нужно сравнить длину двух стержней. Если стержни не двигаются друг относительно друга, то сделать это несложно. Нужно только приложить их друг к другу и удостовериться, совпадают ли их концы. Сравнение движущихся отрезков осуществить сложнее.

Пусть стержни а и б параллельны и стержень б движется со скоростью v перпендикулярно самому себе (рис. 31). Для сравнения длины стержней от концов стержня а пошлем лучи света в направлении, перпендикулярном стержню. Если эти лучи попадают точно на концы стержня б, то оба стержня, следовательно, имеют одинаковую длину. Результат измерения не зависит от того, движется ли стержень б и с какой скоростью он движется.

Рис. 31. Сравнение длин движущихся стержней в случае, когда стержни перпендикулярны направлению их относительного движения. Пупктирные линии изображают световой луч, направленный из конца одного стержня к концу другого

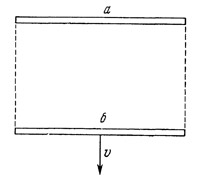
В системе отсчета, связанной со стержнем а, стержни а и б равны по длине. Точно к такому же выводу придет наблюдатель, покоящийся относительно стержня б. Посланные из концов стержня б перпендикулярно ему световые лучи угодят точно в концы стержня а. И в системе стержня б стержни а и б будут иметь одинаковую длину. Мнения наблюдателей в разных инерциальных системах относительно длины стержней полностью совпадают. Это показывает, что размеры тела, перпендикулярные направлению движения, не зависят от инерциальной системы, в которой мы измеряем тело (иначе говоря, не зависят от скорости тела). Этот факт мы уже использовали раньше, когда на рис. 26 и 27 предполагали, что расстояние от часов В до зеркала не зависит от системы отсчета. А как сравнить стержни, если они параллельны и один из них движется по отношению к другому концом вперед (рис. 32), т. е. стержни все время параллельны направлению их относительного движения. Теперь сравнение стержней можно произвести только в некоторый определенный момент времени, не раньше и не позже.

Рис. 32. Сравнение длин движущихся стержней, когда стержни параллельны направлению относительного движения. Такие стержни можно сравнивать в тот момент, когда концы А и А` совпадают

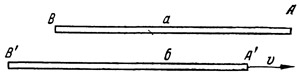
Если соответствующие концы стержней а и б совпадают в один и тот же момент времени, то стержни имеют одинаковую длину. Если сначала совпадут концы А и А` и только затем концы В и В` то стержень б несомненно длиннее стержня а.

Сравнивая стержни, мы употребили понятие одновременности событий. Одновременность же зависит от системы отсчета. События, одновременные в одной инерциальной системе, не будут такими в другой. Следовательно, если оба конца стержней в некоторой инерциальной системе совпадают в один и тот же момент времени, то в других инерциальных системах это происходит в различные моменты времени.

Подчеркнем еще раз, что зависимость длины от инерциальной системы имеет место только для размеров в направлении движения. Длины, измеряемые в перпендикулярном движению направлении, не зависят от инерциальной системы.

Рассмотрим пример с поездом, о котором шла речь выше. Там наблюдатель, стоящий у насыпи, видел, что молнии у паровоза и у последнего вагона поезда сверкнули одновременно (следы молний при этом остались и на пути железной дороги), следовательно, длина поезда для наблюдателя у насыпи была равна расстоянию между следами молний. А что сказал бы об этом пассажир, находящийся в среднем вагоне поезда? По его мнению, молния у паровоза сверкнула раньше, чем у последнего вагона. Это значит, что передний конец поезда совпал со следом молнии раньше, чем задний. Следовательно, для пассажира, едущего в среднем вагоне состава, поезд будет длиннее, чем расстояние между метками молний па железнодорожном пути. Наблюдатель, стоящий у насыпи железной дороги, измерив длину движущегося поезда, получит меньшую величину, чем наблюдатель в поезде, который считает поезд покоящимся. Размеры движущегося тела меньше покоящегося. Нетрудно найти формулу, которая показывает зависимость размеров тела (в направлении движения) от скорости.

Предположим, что в описанном в § 6 опыте с часами и сигналами света наблюдатель в системе часов А измеряет расстояние между часами А и А`. Пусть оно будет равно l_o. Именно настолько часы В сместились, пока сигнал света был в пути, т. е. часы В сместились на l_o м за время t₀ сек. Скорость часов В относительно часов А будет равна

v = l_o/t_o (a)

Допустим, что одновременно с наблюдателем у часов А наблюдатель у часов В также измеряет расстояние между часами А и А` и пусть в результате измерения он получит 1м, т. е. длину, на которую часы А сместились за время t. Скорость часов А относительно часов В тогда будет равна

v=l/t (б)

Скорость часов В относительно часов А равна скорости часов А относительно часов В (то, что скорости направлены противоположно друг другу, нас в данном случае не интересует), поэтому мы и обозначали их одной и той же буквой v. Из равенств (а) и (б) следует:
l_o/t_o = l/t
Умножив обе части полученного соотношения на t и подставив затем выражение г из формулы (3), получим

l = l_о √ (1 — v²/c²). (4)

Таким образом, мы получили формулу, которая показывает зависимость размеров тела от скорости в направлении движения. Если длина покоящегося тела равна l_о, то длина движущегося со скоростью v тела определяется формулой (4)

Чем больше скорость тела, тем короче оно по сравнению с другим точно таким же, но покоящимся телом. Не ведет ли такое следствие теории относительности к противоречиям?

Чтобы ответить на этот вопрос, рассмотрим следующий пример.

Пусть на аэродроме стоят два одинаковых самолета. Предположим далее, что один из них поднимается в воздух, делает крут над городом и с громадной скоростью проносится над самолетом, оставшимся на аэродроме. Наблюдатель, оставшийся на Земле, сравнив размеры летящего самолета с размерами самолета на аэродроме, обнаружит, что пролетевший над аэродромом самолет оказывается короче. Пусть в это же самое время размеры самолетов сравнивает также летчик в воздухе. С его точки зрения его самолет покоится, а аэродром с оставшимся на нем самолетом мчится ему навстречу. Согласно наблюдениям летчика, самолет на земле оказывается короче самолета в воздухе. Заключения наблюдателя на земле и летчика только кажутся противоречивыми. В этом кажущемся противоречии отражается закон природы: длина тела — понятие относительное. Нельзя говорить о длине тела, не указав, в какой системе отсчета эта длина измерена. Чем быстрее движется тело относительно инерциальной системы, тем короче оно в этой системе. Тело длиннее всего в той системе отсчета, где его скорость равна нулю (напомним, что речь идет все время о размерах тела в направлении движения.).

Как и все явления, предсказанные теорией относительности, сокращение тел в направлении движения незаметно при малых скоростях. Для велосипедиста, развивающего, например, скорость 18 км/час относительно шоссе, все земные предметы будут сокращаться в направлении его движения только на 0,000 000 000 000 01 %. Если смотреть с самолета, летящего со скоростью 500 км/час, предметы на поверхности земли окажутся укороченными на 0,000 000 000 01%. Это значит, что, например, расстояние между Таллином и Тарту пассажиру этого самолета будет казаться всего лишь на 1,5 стотысячных миллиметра короче, чем показывают наземные измерения. Даже скорости небесных тел слишком малы для того, чтобы можно было обнаружить сокращения, вызванные этими движениями. Солнце, например, движется относительно Земли со скоростью 30 км/сек. Обусловленное этим движением процентное сокращение диаметра Солнца в направлении движения составит 0,000 000 5%, т. е. всего-навсего 7 м. При измерении расстояния в 150 млн. км, отделяющего нас от Солнца, такая малая величина вообще несущественна.

Для скоростей, сравнимых со скоростью света, сокращение тел в направлении движения должно быть заметным. В табл. 4 представлена зависимость длины от скорости для случая, когда длина неподвижного тела равна одному метру.

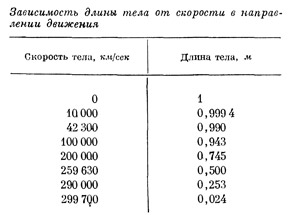
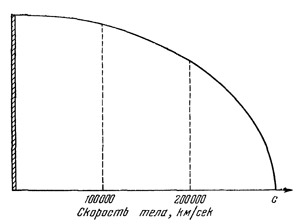
Наглядно зависимость сокращения тела в направлении движения изображена на рис. 33. На левом краю рисунка изображен стержень такой длины, которую он имеет, будучи неподвижным. Если мы хотим определить длину этого стержня, когда он движется (концом вперед) со скоростью, окажем, 100 000 км/сек, то достаточно измерить расстояние от кривой до точки на горизонтальной оси, где указано число 100 000. Это и будет соответствовать длине стержня, движущегося со скоростью 100 000 км/сек.

На рисунке видно, что, когда скорость тела приближается к скорости света, длина стержня стремится к нулю. Если бы стержень двигался точно со скоростью света, то его длина была бы равна нулю, т. е. стержень перестал бы существовать. Отсюда видно, что скорость любого тела всегда должна быть меньше скорости света. Со скоростью света могут двигаться только такие объекты, которые не имеют геометрической формы.

Таковы, например, «частицы» света — фотоны, о которых будет идти речь ниже.

Рис. 33. Зависимость длины тела от скорости

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle

Источник