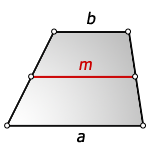
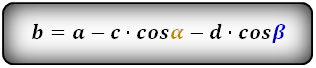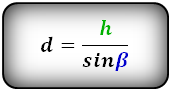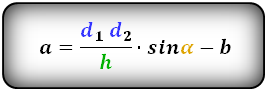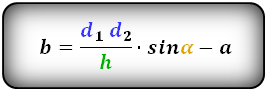Как найти длину трапе - Исправление недочетов и поиск решений вместе с Examum.ru

1. Формула длины основания трапеции через среднюю линию

a — нижнее основание

b — верхнее основание

m — средняя линия

Формулы длины оснований :

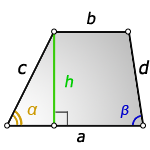
2. Формулы длины сторон через высоту и углы при нижнем основании

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

α, β — углы трапеции

h — высота трапеции

Формулы всех четырех сторон трапеции:

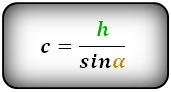
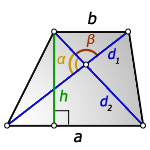
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями

a — нижнее основание

b — верхнее основание

d₁ , d₂— диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

Формулы длины сторон трапеции:

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Подробности

Опубликовано: 21 сентября 2013

Обновлено: 13 августа 2021

Источник

Трапеция. Формулы, признаки и свойства трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

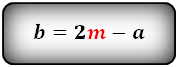
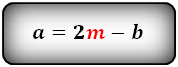
1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m — b

b = 2m — a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a — h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a — c·cos α — d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Определение.

Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
2m	2m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² — 2ad·cos β

d₂ = √a² + c² — 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab —	a(d ² — c²)
a — b

d₂ =	√	c² + ab —	a(c² — d ²)
a — b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a — h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a — h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab — d₂²

d₂ = √c² + d ² + 2ab — d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c² —	(	(a — b)² + c² — d ²	)	²
2	2(a — b)

5. Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
\|a — b\|

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
4√p(p — a)(p — c)(p — d₁)

где

a — большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Источник

Трапеция и ее свойства

Т. А. Унегова

Определения:

Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: $m=displaystyle frac{a+b}{2}$ .

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: $EF=GH, ; FG=displaystyle frac{a-b}{2}$ .

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN .

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: $S=displaystyle frac{a+b}{2}cdot h$ .

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh .

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: $S=displaystyle frac{1}{2}d_1d_2{sin alpha }$ , где d_1=AC, d_2=BD, (Вместо можно брать

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr . Таким образом, $S=displaystyle frac{a+b+c+d}{2}cdot r$ .

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2} .

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины . Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2 .

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол ${150}^{{}^circ }$ . Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна ${180}^{{}^circ }$ , и тогда angle BAH $=30{}^circ .$

Из ABH найдем высоту BH. Катет, лежащий против угла в ${30}^{{}^circ }$ , равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна $S=displaystyle frac{6+18}{2}cdot 3,5=42$ .

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и . Отсюда получаем, что середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть

Периметр трапеции равен

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол $63{}^circ$ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов $vartriangle ACD=3alpha +63{}^circ =180{}^circ$ , откуда
$alpha =39{}^circ .$
Итак, $angle D=78{}^circ$ , а $angle BCD=180{}^circ -78{}^circ =102{}^circ$ .

Ответ: $78{}^circ , 102{}^circ$ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и $h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32.$ Отсюда,

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен ${135}^circ$ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом $45{}^circ$ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна $displaystyle frac{2+4,8}{2}cdot 1,4=4,76$ .

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м ^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции $S=displaystyle frac{a+b}{2}cdot h$ , то $60=displaystyle frac{8+12}{2}cdot h$ , откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны Найдите площадь трапеции.

Решение:

Проведем CE BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что $S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2$ .

Ответ: $displaystyle frac{1}{2}a^2$

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен $60{}^circ$ .

Решение:

По условию задачи в прямоугольном ACD

angle D $=60{}^circ$ , следовательно, angle CAD $=30{}^circ$ .

Так как AC — биссектриса, то angle CAB $=30{}^circ$ , откуда angle DAB $=60{}^circ$ , то есть, трапеция равнобедренная. angle BCA =angle CAD $=30{}^circ$ как накрест лежащие, поэтому ABC — равнобедренный.

Обозначим длины боковых сторон ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном ACD против угла в $30{}^circ$ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом $60{}^circ$ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что BCM равносторонний и BM = 2, тогда AM = 12 и BCM подобен ADM c коэффициентом .

Пусть $S_{BCM}$ =S_1 , $S_{ADM}=S_2$ , тогда

$S_2=k^2cdot S_1=36{cdot S}_1.$

Площадь трапеции будет равна

$S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.$

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна $90{}^circ$ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна $90{}^circ$ , то $angle BEC=90{}^circ$ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh , а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то , откуда r=1,2 .

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

откуда

Сторона AB равна диаметру окружности, поэтому r=3 .

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

$m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.$

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна $180{}^circ$ . Она делится на три равные части по $60{}^circ .$

Вписанный угол D опирается на дугу ABC, которая равна $120{}^circ$ , отсюда $angle ADC=60{}^circ$ и, стало быть, $angle C=120{}^circ =angle B.$

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Загрузить PDF

Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции. При помощи известных величин, а также геометрических и тригонометрических правил можно найти неизвестные стороны трапеции.

1

Запишите формулу для вычисления периметра трапеции. Формула: , где – периметр, – верхнее основание, – нижнее основание, – левая боковая сторона, – правая боковая сторона.^[1]
2
В формулу подставьте известные длины сторон. Не используйте этот метод, если не даны значения всех четырех сторон.
- Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид:
3

Сложите длины сторон. Так вы найдете периметр трапеции.

Реклама

1
Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.
- Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.
2
Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.^[2]
- Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).
3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.^[3] Не используйте этот метод, если не дано значение верхнего основания.
- Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.
4

Запишите теорему Пифагора для первого прямоугольного треугольника. Формула: $a^{{2}}+b^{{2}}=c^{{2}}$ , где – гипотенуза треугольника (сторона, противоположная прямому углу), – высота треугольника, – основание треугольника.^[4]
5
6

Возведите в квадрат известные значения. Затем при помощи вычитания обособьте переменную .
7

Извлеките квадратный корень, чтобы найти . (Чтобы получить информацию об упрощении квадратных корней, прочитайте эту статью.) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.
8

Найдите неизвестную сторону второго прямоугольного треугольника. Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны,^[5]то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого.
9

Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников. В интернете поищите информацию о том, как складывать квадратные корни, или просто воспользуйтесь калькулятором, чтобы преобразовать квадратные корни в десятичные дроби.

Реклама

1
Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.
- Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.
2
Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.^[6]
- Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).
3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.^[7]
- Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.
4
5
В формулу синуса подставьте известные величины. Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.
- Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так:
  $sin(35)={frac {6}{H}}$
6
Найдите синус угла. Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.
- При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид:
  $0,5738={frac {6}{H}}$
7

Найдите переменную H. Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.
8

Найдите гипотенузу второго прямоугольного треугольника. Напишите функцию (формулу) синуса угла второго прямоугольного треугольника: $sin theta ={frac {B}{H}}$ . Так вы найдете гипотенузу второго треугольника, которая является второй боковой стороной трапеции.
9

Запишите теорему Пифагора для первого прямоугольного треугольника. Формула: $a^{{2}}+b^{{2}}=c^{{2}}$ , где – гипотенуза треугольника (сторона, противоположная прямому углу), – высота треугольника.
10
11

Найдите . Вы получите основание первого прямоугольного треугольника, которое является первой неизвестной частью нижнего основания трапеции.
12
13
Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников.
- В нашем примере:
  Таким образом, приблизительный периметр трапеции равен 45,5059 см.
Реклама

Советы

Для специальных прямоугольных треугольников (треугольник 30-60-90^[8] или треугольник 90-45-45^[9]) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора.
Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.^[10]

Что вам понадобится

Калькулятор
Карандаш
Бумага

Об этой статье

Эту страницу просматривали 119 038 раз.

Была ли эта статья полезной?

Источник

Как найти длину основания трапеции

Для задания такого четырехугольника, как трапеция, должно быть определено не менее трех его сторон. Поэтому, для примера, можно рассмотреть задачу, в условии которой заданы длины диагоналей трапеции, а также один из векторов боковой стороны.

Инструкция

Фигура из условия задачи представлена на рисунке 1.В данном случае следует предположить, что рассматриваемая трапеция – это четырехугольник AВCD, в котором заданы длины диагоналей AC и BD, а также боковая сторона АВ, представленная вектором a(ax,ay). Принятые исходные данные позволяют найти оба основания трапеции (как верхнее, так и нижнее). В конкретном примере сначала будет найдено нижнее основание АD.

Рассмотрите треугольник ABD. Длина его стороны АВ равна модулю вектора a. Пусть|a|=sqrt((ax)^2+(ay)^2)=a, тогда cosф =ax/sqrt(((ax)^2+(ay)^2), как направляющий косинус a. Пусть заданная диагональ BD имеет длину p, а искомая AD длину х. Тогда, по теореме косинусов, P^2=a^2+ x^2-2axcosф. Или x^2-2axcosф+(a^2-p^2)=0.

Решения этого квадратного уравнения:X1=(2acosф+sqrt(4(a^2)((cosф)^2)-4(a^2-p^2)))/2=acosф+sqrt((a^2)((cosф)^2)-(a^2-p^2))==a*ax|sqrt(((ax)^2+(ay)^2)+sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+ p^2)=AD.

Для нахождения верхнего основания ВС (его длина при поиске решения также обозначена х) используется модуль |a|=a, а также вторая диагональ BD=q и косинус угла АВС, который, очевидно, равен (п-ф).

Далее рассматривается треугольник АВС, к которому, как и ранее, применяется теорема косинусов, и возникает следующее решение. Учитывая, что cos(п-ф)=-cosф, на основе решения для AD, можно записать следующую формулу, заменив p на q:ВС=- a*ax|sqrt(((ax)^2+(ay)^2)+sqrt((((a)^2)(ax^2))/(ax^2+ay^2))-a^2+q^2).

Данное уравнение является квадратным и, соответственно, имеет два корня. Таким образом, в данном случае остается выбрать лишь те корни, которые имеют положительное значение, так как длина не может быть отрицательной.

ПримерПусть в трапеции АВСD боковая сторона АВ задана вектором a(1, sqrt3), p=4, q=6. Найти основания трапеции.Решение. Используя полученные выше алгоритмы можно записать:|a|=a=2, cosф=1/2. AD=1/2+sqrt(4/4 -4+16)=1/2 +sqrt(13)=(sqrt(13)+1)/2.BC=-1/2+sqrt(-3+36)=(sqrt(33)-1)/2.

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник