Как найти длину трапеции на клетчатой бумаге

Это задание из ОГЭ по математике предлагает найти площади, углы, длины геометрических фигур, нарисованных на фоне в клетку. Задание 18 с кратким ответом, в ответ идет только число.

Реальные задания №18 по геометрии из банка ФИПИ

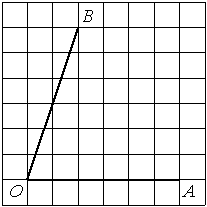
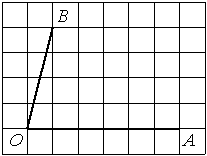
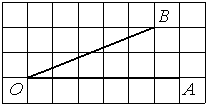
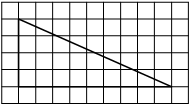
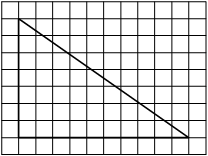
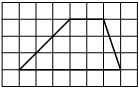
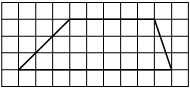
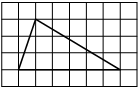
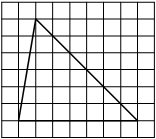
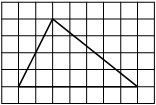
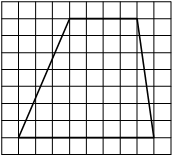
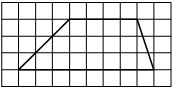
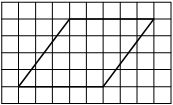
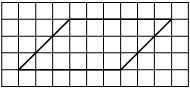
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=6/2=3.
Ответ: 3

AE8B22

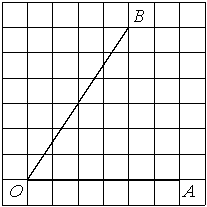
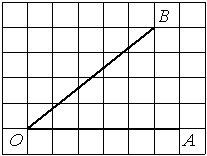
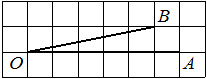
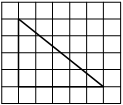
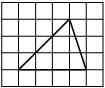
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=6/4=1,5.
Ответ: 1,5

09C3B1

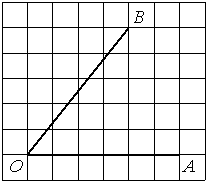
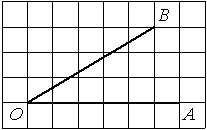
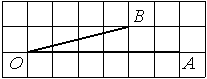
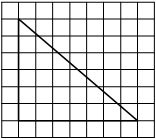
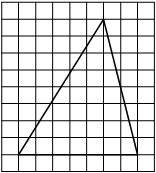
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=5/4=1,25.
Ответ: 1,25

739060

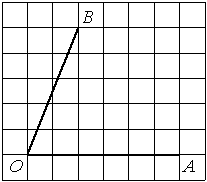
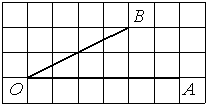
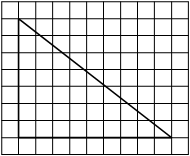
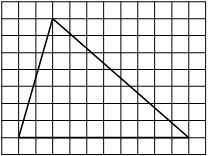
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=5/2=2,5.
Ответ: 2,5

0747AA

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=4/1=4.
Ответ: 4

9C09A9

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=4/5=0,8.
Ответ: 0,8

A1ECAA

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=3/5=0,6.
Ответ: 0,6

887E42

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=2/4=0,5.
Ответ: 0,5

201054

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=2/5=0,4.
Ответ: 0,4

E73651

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=1/5=0,2.
Ответ: 0,2

A601D0

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:  tgAOB=1/4=0,25.
Ответ: 0,25

51BEC9

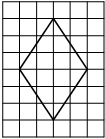
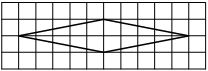
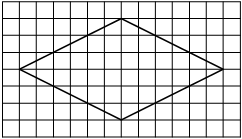
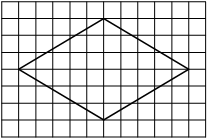
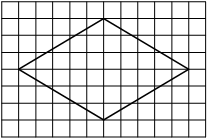
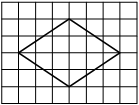
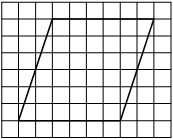
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*4=12
Ответ: 12

F519DD

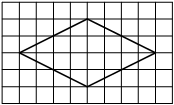
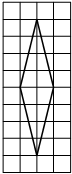
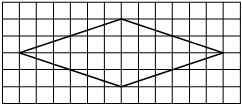
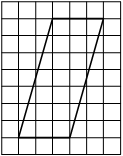
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10*2=10
Ответ: 10

704DB1

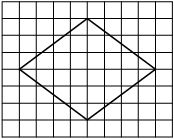
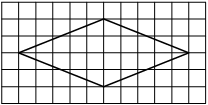
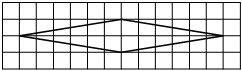
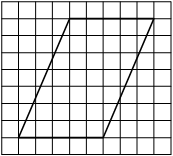
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*8=24
Ответ: 24

2F4DA5

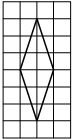
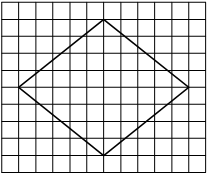
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*2=6
Ответ: 6

1F239C

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 8  * 4 = 16
Ответ: 16

33E327

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 6 = 36
Ответ: 36

0B92D0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 2 = 8
Ответ: 8

3B5D8B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 4 = 20
Ответ: 20

CFCA33

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 8 = 40
Ответ: 40

3B008A

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 6 = 30
Ответ: 30

8372E0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 4 = 24
Ответ: 24

FFD1EE

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 2 = 12
Ответ: 12

E2A932

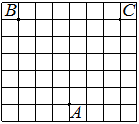
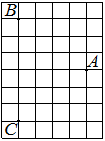
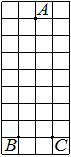
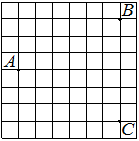
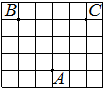
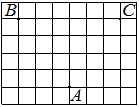
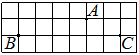
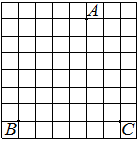
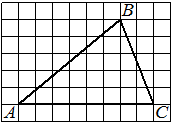
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3

969F4E

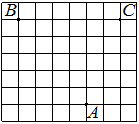
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5

AFB9A1

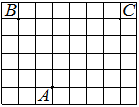
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1

D234F7

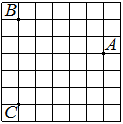
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2

68F679

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 4

9672D7

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5

3F311F

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6

C598DA

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 8

FCC29D

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7

0DBF9B

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6

B73FA9

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1

78BDFE

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7

CB1715

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3

107F53

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2

5B4C37

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

FEDC09

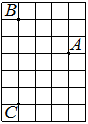
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6

C563EA

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5

B2853A

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

FE13B1

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2

C8BF73

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5

A4B62F

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2

DA3762

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 7

C576A6

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 1

9D880E

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

078B48

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6

854014

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 3

B4DCCF

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 8

259D23

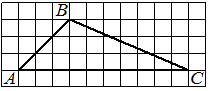
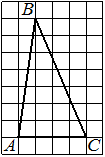
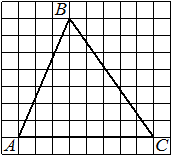
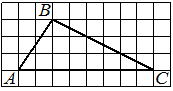
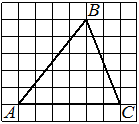
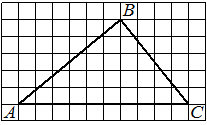
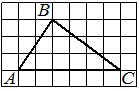
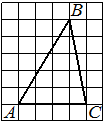
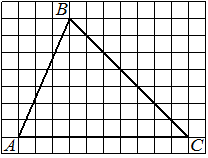
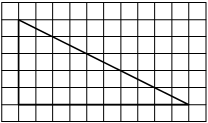
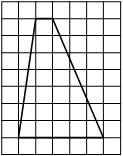
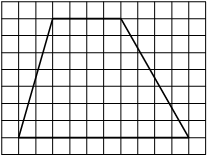
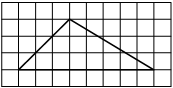
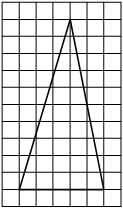
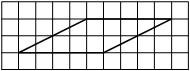
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

9C2804

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

BC4EBE

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

7ECBCE

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

D2D94B

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

8F5C52

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

686EFB

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

07C968

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

E3456A

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

794271

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

A1906B

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

E52B99

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

E331C7

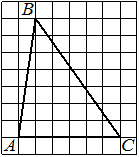
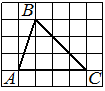
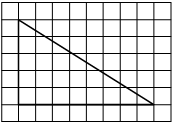
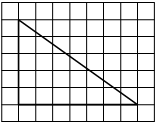
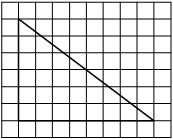
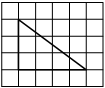
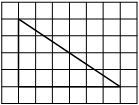
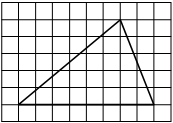
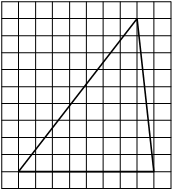
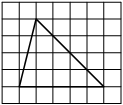
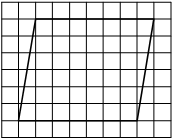
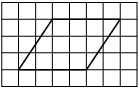
На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6

F7FF65

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8

AAC1BC

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7

2BD44A

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8

6DE9A6

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 4

39A91A

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9

197283

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 5

2EA9C2

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7

ED1F0E

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9

10323E

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10

ED4E1A

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6

4FAEEC

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10

F8232E

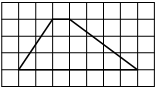
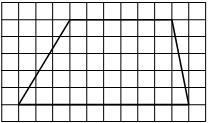
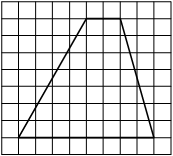
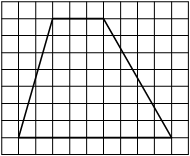
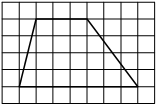
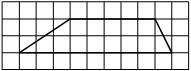
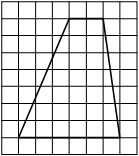
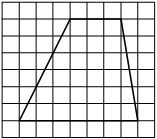
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+7) : 2 = 4
Ответ: 4

351A72

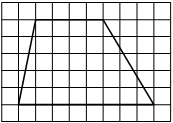
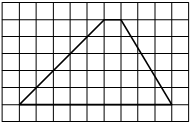
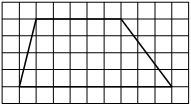
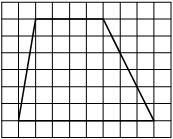
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (6+10) : 2 = 8
Ответ: 8

5EFE19

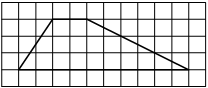
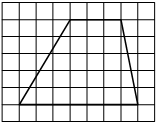
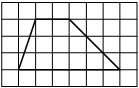
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (4+8) : 2 = 6
Ответ: 6

C05266

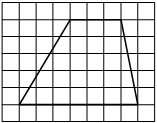
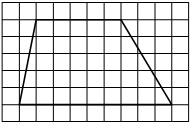
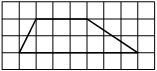
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+10) : 2 = 6
Ответ: 6

CFD6D8

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (3+7) : 2 = 5
Ответ: 5

3BD771

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+8) : 2 = 5
Ответ: 5

869450

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+5) : 2 = 3
Ответ: 3

19D522

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+6) : 2 = 4
Ответ: 4

A28F9D

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+9) : 2 = 5
Ответ: 5

2EF821

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (3+9) : 2 = 6
Ответ: 6

45A5FF

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (5+9) : 2 = 7
Ответ: 7

7AAADC

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (4+10) : 2 = 7
Ответ: 7

321F00

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

87C214

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6

6CB64A

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

4801B0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

DEA70E

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

6D0D8F

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

8D9098

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

90A16B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

F3D7EA

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

35106F

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

1C594B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6

E4F439

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

657F97

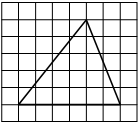
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 3 = 9
Ответ: 9

E873D3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 5 = 20
Ответ: 20

9E69AF

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 3 = 12
Ответ: 12

53C928

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 5 = 15
Ответ: 15

EE2C25

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 10 = 25
Ответ: 25

1B4EAF

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 9 = 36
Ответ: 36

94B40E

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 4 = 10
Ответ: 10

F50FF8

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 6 = 21
Ответ: 21

3A7F81

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 4 * 3 = 6
Ответ: 6

DFB4EA

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 8 = 28
Ответ: 28

7AEBD7

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 10 * 7 = 35
Ответ: 35

4718F7

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 2 = 14
Ответ: 14

0C5645

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (7+3) * 4= 20
Ответ: 20

695D77

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 7= 42
Ответ: 42

07B1AD

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 3 = 18
Ответ: 18

4774FE

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 2= 14
Ответ: 14

284762

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 4= 28
Ответ: 28

2916B2

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 5= 25
Ответ: 25

867701

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 5= 35
Ответ: 35

B5D99F

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 7= 28
Ответ: 28

B11571

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 6= 36
Ответ: 36

E46263

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 3= 12
Ответ: 12

283DE4

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 2= 10
Ответ: 10

383C46

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 6= 30
Ответ: 30

2E7B84

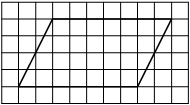
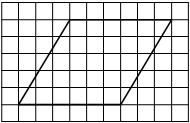
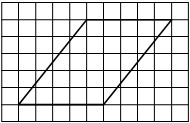
На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 4 = 28
Ответ: 28

71E23E

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 2 = 10
Ответ: 10

3BD9B6

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 4 = 20
Ответ: 20

5C5046

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 3 = 18
Ответ: 18

566A4E

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 6 = 36
Ответ: 36

0275CC

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 3 * 7 = 21
Ответ: 21

E81F8D

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 7 = 35
Ответ: 35

2A59D7

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 2 = 14
Ответ: 14

5FC71A

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 5 = 30
Ответ: 30

257B6F

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 6 = 42
Ответ: 42

839354

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 4 * 3 = 12
Ответ: 12

C1A1AF

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 5 = 25
Ответ: 25

9B4AE0

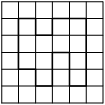
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 14

11403B

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 8

CDF457

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 15

06B968

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 10

AFB70E

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 13

C4025D

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 16

E4CBB2

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 9

211628

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 17

5D3FCF

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 19

320729

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 18

C72856

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 12

BB2950

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 11

F78C61

Всего: 91    1–20 | 21–40 | 41–60 | 61–80 | 81–91

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 91    1–20 | 21–40 | 41–60 | 61–80 | 81–91

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам 

1. На клетчатой бумаге с размером клетки  изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: 

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна Тогда

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

Осталось умножить найденное значение синуса на

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

 , где и — диагонали.

Получим: 

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки  Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна

Площадь каждого из маленьких треугольников равна

Тогда площадь четырехугольника

9. Авторская задача.  Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга 

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в  раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в  раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть круга.

Значит, нам надо умножить площадь круга на . Получим:

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости 

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.