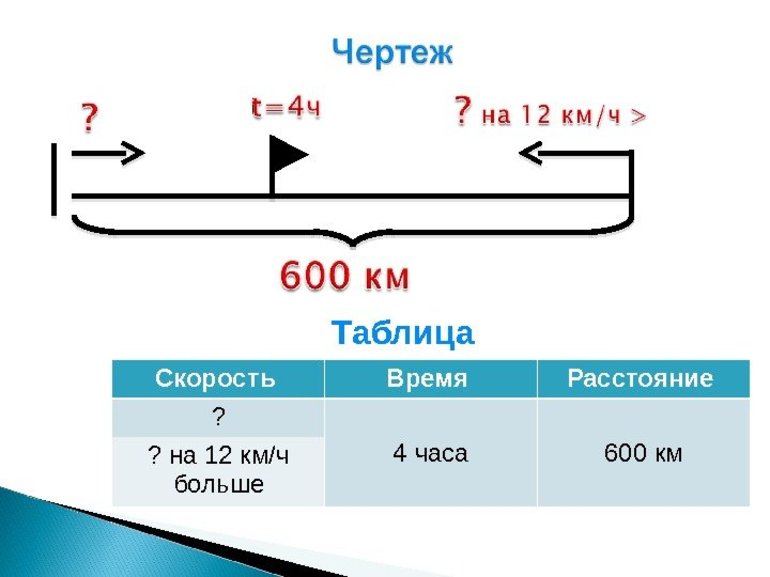
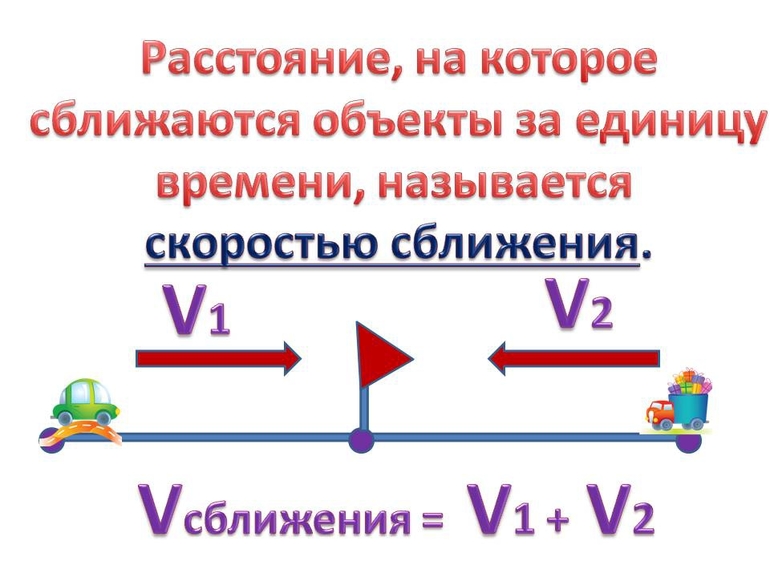
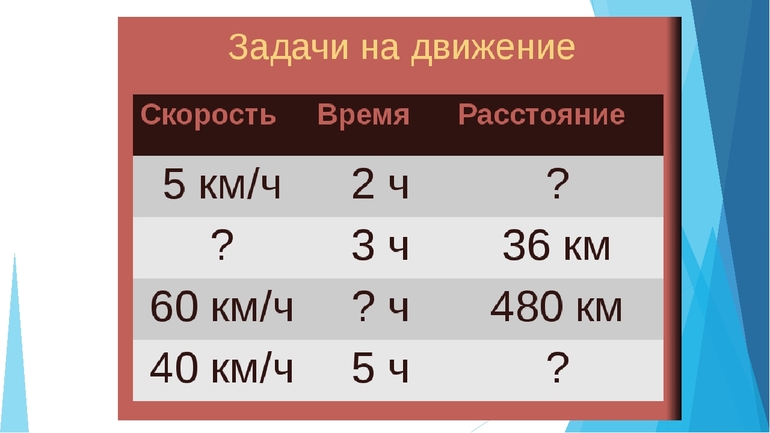
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
В физике следует различать траекторию, путь и перемещение.
Определение 1
Траектория — форма линии, описываемая телом. Ее длина представляет собой путь и является скалярной величиной. Перемещением же называется вектор, соединяющий точки начала и конца пути, и направленный от начала к концу.
Длина пути измеряется в системе СИ в метрах, в СГС (сантиметр, грамм, секунда) — в сантиметрах. Применяются и другие единицы измерения длины, в том числе внесистемные (дюйм, фут, ярд, миля и т.д.).
При движении без ускорения путь равен произведению скорости на расстояние:
$S = v cdot (t_2 — t_1) = v cdot Delta t$,
где $v_0$ – скорость тела, $t_2$ — момент времени окончания движения, $t_1$ — момент времени начала движения, $Delta t$ — время движения. График зависимости пути от времени на координатной плоскости в случае такого, называемого равномерным, движения является прямой линией.
Замечание 1
Поскольку скорость — векторная величина, равномерным можно считать только движение по прямой, т.к. при изменении направления движения вектор не остается неизменным даже при сохранении его длины.
Если равноускоренное движение начато с нулевой скорости и известно ускорение, то формула пути имеет вид
$S = frac{a cdot t^{2}}{2}$
где $a$ – ускорение тела.
Объединив два условия, получим общую формулу нахождения пути при равноускоренном движении с произвольной начальной скоростью:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$.
Если движение не равномерное и известна средняя скорость движения, то путь можно выразить и другим способом:
$S = v_{ср.} cdot Delta t$,
где $v_{ср.}$ — средняя скорость движения.
На практике движение бывает равномерным или равноускоренным лишь на небольших фрагментах пути, поэтому для вычисления его длины траекторию разбивают на участки, где тело движется по простым закономерностям, вычисляют длину каждого из них и суммируют. Если известна траектория, то ее разбивают на фрагменты, каждый из которых имеет простую геометрическую форму. Сложив их длины, можно найти путь.
Пример 1
Найти путь, пройденный при движении с ускорением 2 $м/с^2$ в течение 20 с, если скорость на момент начала измерения была равна 10 м/с.
Подставим в формулу численные значения:
$S = frac{a cdot t^2}{2} + v_0 cdot Delta t$
$S = frac{2 cdot 20^2}{2} + 10 cdot 20 = 600 м$.
Ответ: длина пути составила 600 метров.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание материала
- Кинематика
- Видео
- Как выглядит формула пути без времени, когда скорость тела уменьшается
- Импульс
- График скорости равномерного движения
- Виды движения и формулы длины пути
- Основные формулы электричества
- Примеры решения задач
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Центростремительное ускорение находится по одной из формул:
Видео
Как выглядит формула пути без времени, когда скорость тела уменьшается
Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:
[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]
Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:
[ large begin{cases} S = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v = v_{0} — a cdot t end{cases} ]
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
График скорости равномерного движения
Т.к. скорость – это векторная величина, она характеризуется и модулем, и направлением. В зависимости от выбранного направления скорость по знаку может быть как положительной, так и отрицательной.
На рисунке 1 изображен динозавр, автомобиль и дом. Зададим ось координат $x$.
Если динозавр начнет двигаться к дому, то его скорость будет положительной, т.к. направление движения совпадает с направлением оси $x$. Если же динозавр направится к автомобилю, то его скорость будет отрицательной, т.к. направление движения противоположно направлению оси $x$.
Итак, график скорости равномерного движения имеет вид, представленный на рисунке 2.
Из графика видно, что скорость с течением времени не изменяется – она постоянна в любой выбранный момент времени. Из графика положительной скорости мы видим, что $upsilon = 6 frac{м}{с}$; из графика отрицательной — $upsilon = -4 frac{м}{с}$.
Зная скорость и время, мы можем рассчитать пройденный путь за определенный промежуток времени. Рассчитаем какой путь пройдет тело с положительной скоростью за $4 с$.
$$S = upsilon t = 6 frac{м}{с} cdot 4 c = 24 м$.$
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $Delta s$ на отрезке времени от $t$ до $t + Delta t$ находят как:
где $langle vrangle$ – средняя путевая скорость. При равномерном движении $langle vrangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
где a – постоянное ускорение, v – начальная скорость движения.
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Примеры решения задач
1. Самым быстрым животным на Земле считается гепард. Он способен развивать скорость до $120 frac{км}{ч}$, но сохранять ее способен в течение короткого промежутка времени. Если за несколько секунд он не настигнет добычу, то, вероятнее всего, уже не сможет ее догнать. Найдите путь, который пробежит гепард на максимальной скорости за $3$ секунды.
Переведем единицы измерения скорость в СИ и решим задачу.
$120 frac{км}{ч} = 120 cdot frac{1000 м}{3600 с} approx 33 frac{м}{с}$.
Дано:$upsilon=120 frac{км}{ч}$$t = 3 c$СИ:$upsilon=33 frac{м}{с}$
Найти:$S — ?$
Показать решение и ответ
Скрыть
Решение:
Гепард двигается равномерно в течение 3 с.
Путь, который он проходит за это время:
$S = upsilon t = 33 frac{м}{с} cdot 3 с approx 100 м$
Ответ: $100 м$
2. Колибри – самые маленькие птицы на нашей планете. При полете они совершают около 4000 взмахов в минуту. Тем не менее, они способны пролетать очень большие расстояния. Например, некоторые виды данной птицы перелетают Мексиканский залив длиной $900 км$ со средней скоростью $40 frac{км}{ч}$. Сколько времени у них занимает такой полет?
Переведем единицы измерения скорость в СИ и решим задачу.
$40 frac{км}{ч} = 40 cdot frac{1000 м}{3600 с} approx 11 frac{м}{с}$;
$900 км = 900 000 м$.
Дано:$upsilon_{ср} = 40 frac{км}{ч}$$S = 900 км$CИ:$upsilon_{ср} = 11 frac{м}{с}$$S = 900 000 м$
Найти:$t-?$
Показать решение и ответ
Скрыть
Решение:
Полет колибри будет примером неравномерного движения. Зная среднюю скорость и путь, рассчитаем время перелета:
$t = frac{s}{upsilon_{ср}} = frac{900 000 м}{11 frac{м}{с}} approx 82 000 с$.
Переведем время в часы:
$1 ч = 60 мин = 60 cdot 60 c = 3600 c$.
Тогда,
$t = frac{82 000 c}{3600 c} approx 23 ч$.
Ответ: $t = 82 000 c = 23 ч$.
Теги
Понятие о времени
Существует характеристика, с которой приходится сталкиваться каждый день вне зависимости от возраста, социального статуса, различных способностей и умений. С её помощью определяют будущее, прошедшее и настоящее. По сути, это маркер, определяющий событие. Называют его временем. Рассматривая движение, всегда учитывают эту характеристику, как и её прогрессию.
Время является частью пространственной координаты. Но если относительно других осей можно перемещаться в различных направлениях, относительно него движение определяется только вперёд или назад. Неотъемлемой частью, связанной со временем, является пространство, благодаря которому и возможно понять суть параметра.
Исследованием характеристики занимались философы и учёные в различные периоды существования человечества. Видеть и слышать время невозможно, в отличие от осязаемого пространства, которое возможно наблюдать сразу и везде. Причём в нём можно перемещаться.
Дискуссии, как правильно воспринимать время, не утихают до сих пор. Платон считал, что оно есть не что иное, как движение. Аристотель предполагал, что время — количественное измерение перемещения. Оно было добавлено к классической геометрии Евклида, действующей на ограниченное число измерений. В итоге стало рассматриваться четырёхмерное пространство.
Сегодня так и нет ответов на следующие вопросы о времени:
- из-за чего происходит его течение;
- почему оно определяется только в одном направлении;
- является ли параметр одномерным, как многие учёные считают;
- можно ли обнаружить кванты характеристики.
В классической физике для определения временного изменения используется специальная координата пространство-время. Принято будущие события обозначать знаком плюс, а прошедшие минусом. Единица измерения времени связана с вращением планеты вокруг своей оси и Солнца. Этот выбор был сделан условно и привязан к удобству жизнедеятельности человечества.
В Международной системе единиц принято за секунду принимать интервал, равный 9 192 631 770 периодам излучения атома цезия-133 в покое при нуле градусов по Кельвину. Обозначают параметр латинской буквой t. Таким образом, время — физическая величина, связанная с перемещением какого-либо тела относительно выбранной системы координат.
Расстояние и скорость
Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.
В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:
- начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
- пройденное расстояние можно определить, отняв из конечных координат начальные;
- изменение положения будет нулевым, когда d = p.
В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.
Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.
Одно и то же расстояние можно преодолеть за разное время. Например, чтобы пройти 7 километров человеку понадобится затратить порядка одного часа, на автомобиле же этот путь можно преодолеть за 10 минут, а то и меньше. Вот как раз эти отличия и зависят от скорости движения.
Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.
Общая формула
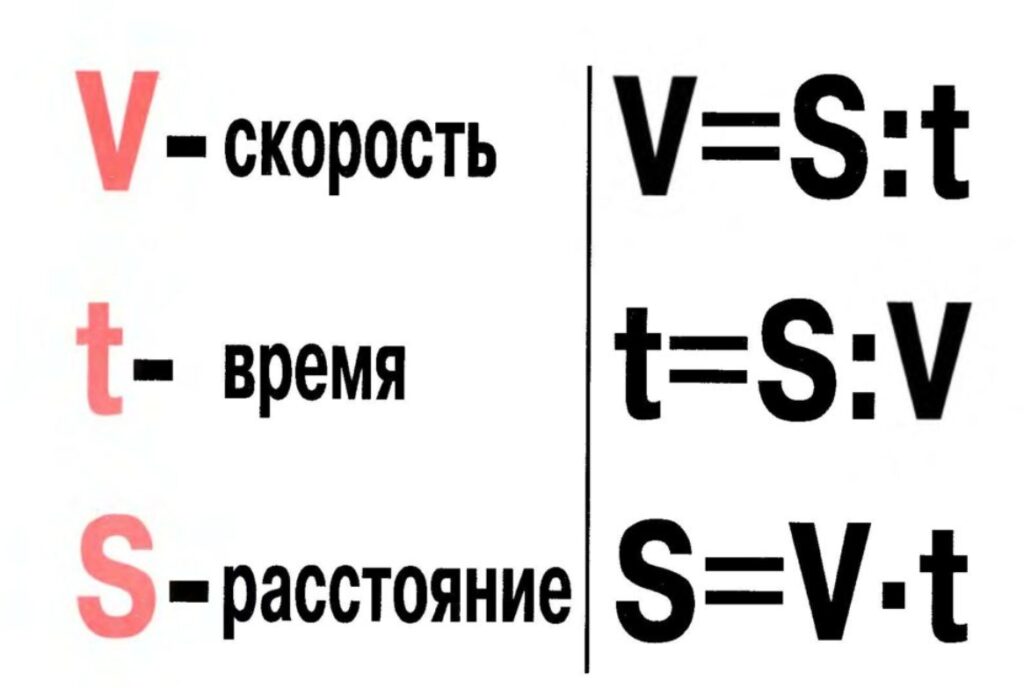
Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:
S = V * t, где:
- S — пройденное объектом расстояние;
- V — средняя скорость тела;
- t — время, затраченное на преодоление пути.
Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).
Действительно, пусть имеется физическое тело, находящееся в каком-то месте. Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2). В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.
Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.
Как видно, выражение, связывающее 3 величины, довольно простое. Но оно не учитывает, что скорость может быть непостоянной, поэтому если объект проходит свой путь неравномерно, в выражение подставляют среднее значение. Находится оно как сумма всех отдельных скоростей на неравномерных участках: Vср = ΔS / Δt.
Решение задач
Чтобы уметь решать простые задания в средних классах по математике, связанных с движением, нужно знать всего одну формулу. При этом необходимо пристальное внимание уделять размерности. Все вычисления осуществляются в СИ. Вот некоторые из типовых заданий, используемые при обучении школьников в четвёртом классе средней школы:
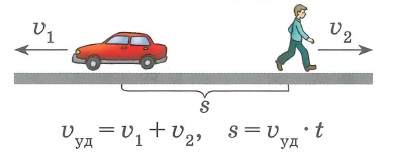
- Из населённого пункта А в точку Б выехала колонна грузовиков. Навстречу им отправился легковой автомобиль. Скорость грузоперевозчиков составляет 80 км/ч, а пассажирской машины 60 км/ч. Встретились они в точке C через полтора часа. Определить расстояние между А и Б. Решение этой задачи будет состоять из нескольких шагов. На первом можно найти путь, который проехала колона: 80 * 1,2 = 96 км. На втором вычислить пройденное расстояние второй: 60 * 1,2 = 72 км. Отсюда общий путь будет равен сумме: АС + СБ = 72 + 96 = 168 км.
- Корабль, скорость которого в стоячих водах равна 30 км/ч, идёт по течению, а после возвращается. Скорость реки равняется трём километрам в час, промежуточная остановка занимает 5 часов. Путь от начала до возврата корабль проходит за 30 часов. Найти, сколько километров составляет весь рейс. Чтобы решить задачу, удобно составить таблицу. В столбцах нужно записать расстояние, скорость и время, а в строках расчётные данные для таких событий, как стоянка, ход по и против течения. Учитывая условие, рабочая формула примет вид: (S / 28) + (S / 22) + 5 = 30. Выражение можно упростить. В итоге должно получиться: 25 * S / 308 = 25 → S = 308. Так как путь корабля состоял из двух одинаковых расстояний, искомое расстояние будет: P = 2 * S = 308 * 2 = 616 км.
- Железнодорожный состав проезжает мост за 45 секунд. Длина переправы составляет 450 метров. При этом стрелочник, смотря прямо, видит проходящий поезд всего 15 секунд. Найти длину состава и скорость его движения. Если принять, что поезд движется со скоростью V, то его длина будет равняться D = 15 * V. Так как состав за 45 секунд проходит расстояние 45 * V = 450 + 15 * V, из равенства легко определить скорость: V = 45 * V – 15 * V = 450 → V = 450 / 3 0 = 15 м / с. Следовательно, длина состава: D = 15 * 15 = 225 м.
Все задачи на движение можно разделить на несколько типов: перемещение навстречу, движение вдогонку, нахождение параметров относительно неподвижного объекта. Но, несмотря на их виды, все они решаются по одинаковому алгоритму, поэтому для удобства можно сделать памятку, указав в ней формулы и размерность величин.
Как найти скорость время расстояние
Добавлено: 12 февраля 2023 в 16:40

Время, расстояние и скорость — три фундаментальные величины, играющие важную роль как в математике, так и в физике. Все вместе они образуют движение, которое и изучают в школе, начиная с 4-го класса.
Теория о данных факторах важна и для подготовки к ЕГЭ по физике, поэтому сегодня мы разберемся с тем, как найти скорость, время, расстояние и понять взаимодействия между указанными параметрами.
К преимуществам темы относят то, что формулы для этих величин просты в запоминании. А при возникновении трудностей в обучении поможет таблица скорости, времени и расстояния.
Скорость время расстояние в ЕГЭ по физике
Понятие о времени
Временем называют особый маркер, который и определяет то или иное событие. Мы сталкиваемся с этим явлением регулярно. Время помогает нам разобраться, где прошлое, где настоящее, а где будущее.
Невозможно рассматривать теорию движения без учета времени, т.к. оно выступает в роли одной из пространственных координат. Однако, если в случае с прочими осями мы можем двигаться в разных направлениях, в случае со временем перемещение возможно только вперед или назад.
Чтобы получше понять правило, нужно разобраться с тем, что собой представляет пространство. Потому что оно объясняет смысл указанного параметра.
Время изучают с античных времен, но с тех пор в науке осталось немало неразрешенных вопросов касающихся этой величины:
- Что является причиной течения времени;
- Почему время может двигаться только по одному направлению;
- Действительно ли время является одномерным параметром;
- Возможно ли определить кванты этого параметра и как это сделать.
Скорость время расстояние в ЕГЭ по физике
Расстояние и скорость
Если смотреть на обсуждаемые величины с точки зрения физики, то можно определить их так:
Расстояние — это размерность длинны, которую выражают в единицах длинны. В каких единицах измеряется пройденный путь? Данная величина измеряется в метрах.
В математике расстоянием называют меру пройденного пути (другими словами, длину). Для определения изменений положений используются оси координат. В чем измеряется расстояние и как обозначается в математике?
В физике путь измеряется в метрах, секундах или часах. А в математике путь измеряется в единицах длины (метрах, метрах в секунду, километрах в час).
Расстояние представляет меру пройденного пути, длину. Для определения изменений положений используют оси координат. Обычно координатная ось X направлена вдоль направления движения, а Y — перпендикулярно ей. В физике координатной осью обычно называют ось, в направлении которой изменяется физическая величина.
В процессе нахождения пройденного пути по общей формуле крайне важную роль играет еще один фактор, называемый скоростью. Она представляет собой параметр быстроты движения объектов.
Скорость время расстояние в ЕГЭ по физике
Скорость можно определить, если известны время и пройденный путь. Подставив эти величины в формулу для пройденного пути, получим формулу для нужного нам неизвестного.
Скорость — параметр скалярный, и путь измеряется в единицах расстояния, а скорость в единицах времени.
Её отмечают, как одну из важнейших математических величин. По причине этого для её определения существуют формулы, которые используются во многих смежных математических дисциплинах.
Эти формулы не только позволяют определить скорость, но и позволяют вывести новые формулы для таких величин, как ускорение, сила, вес и др. На практике для определения скорости используют две основные формулы: формулу скорости равноускоренного движения и формулу ускорения.
Скорость при равноускоренном движении – это скорость тела после истечения определенного промежутка времени.
Скорость время расстояние в ЕГЭ по физике
Общая формула
Время, расстояние и скорость — это фундаментальные, взаимосвязанные параметры. Изучая один из них, невозможно проигнорировать другие ключевые элементы.
Взаимосвязь этих трех величин отображается в общей формуле S = V * t (формула пройденного пути в физике и математике).
- S — обозначает расстояние;
- V — обозначает скорость;
- t — обозначается время, что было потрачено на весь путь.
Выучив это равенство, вы сможете легко определить любой из трех параметров.
Например, S = V * t — это формула того, как найти расстояние, зная скорость и время. Зная расстояние и скорость, вы поймете, как найти время:
- t = S / V.
А параметр скорости определяется так:
- V = S / t.
Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР
Задать вопрос
Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Кандидат физико-математичеких наук. Преподавательский стаж более 10 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.
Читайте также:
Школьный курс физики содержит раздел «кинематика». Большинство задач этого раздела можно решить, рассматривая движение вдоль одной оси — одномерное движение. Его еще называют прямолинейным движением.
Для некоторых задач нужно рассматривать движение на плоскости – двумерный случай.
Вообще, движение тела может происходить:
- вдоль оси – одномерный случай, ось часто именуют, как «Ox»;
- на плоскости;
- в трехмерном пространстве;
Здесь рассмотрим одномерный случай движения — движение тел вдоль оси.
Параметры, описывающие движение
Чтобы описать движение, используют:
- перемещение тела;
- время, в течение которого движение происходило;
- скорость тела;
- начальные и конечные координаты тела;
- траекторию тела;
Траектория – линия, вдоль которой двигалось тело.
Траектория – скаляр, в СИ длину траектории измеряют в метрах.
Для криволинейного движения траектория будет отрезком кривой.
Если движение прямолинейное, траектория – отрезок прямой линии.
Перемещение тела – это вектор. Он соединяет точки, в которых тело находилось в начале и конце движения, направлен из начальной точки в конечную.
Модуль этого вектора – его длину, в СИ измеряют в метрах.
Может ли перемещение тела равняться нулю, при том, что траектория имеет какую-либо протяженность?
Да, такое может быть. Когда тело движется так, что в конце движения оно вернется в начальную точку, в которой находилось перед началом движения.
Если в завершении движения тело окажется на каком-то расстоянии от начальной точки, длина вектора перемещения будет положительной.
Примечания:
- Модуль (длина) вектора не бывает отрицательным, он либо положительный, либо нулевой.
- Когда тело движется по прямой и не меняет направление, длина траектории совпадает с длиной (модулем) перемещения.
Уравнение движения — описывает характер движения.
Оно содержит:
- время движения,
- начальную и конечную координаты тела и
- его скорость.
Вместо координат тела уравнение движения может содержать перемещение.
Примечания:
- Координаты тела, время движения и траектория – это скалярные величины.
- А скорость тела, его ускорение и перемещение – это векторы.
- Когда движение равномерное, скорость тела не меняется.
- Скорость отвечает на вопрос: как быстро изменяется координата (или путь, перемещение).
Описанные параметры применяют и для равномерного и для неравномерного движения.
Прямолинейное движение вдоль оси
Рассмотрим движение по прямой, когда скорость тела не меняется. Это — равномерное прямолинейное движение.
На рисунке 1 представлено движение тела вдоль оси, назовем ее для определенности Ox:
Рис. 1. Перемещение – это разница между конечной и начальной координатами тела
Ось «Ox» на рисунке 1 обозначена большим символом «X».
Точка, в которой тело находилось в начале движения (x_{0} left( text{м} right)) — начальная координата тела;
В эту точку тело переместилось к концу движения (x left( text{м} right)) — конечная координата тела;
Расстояние между двумя точками (S left( text{м} right)) – это перемещение тела. Перемещение – это вектор.
Формула перемещения для одномерного случая
Для движения по оси (одномерный случай), длину перемещения находят так:
[ large boxed { S = left| x — x_{0} right| }]
Знак модуля нужен для того, чтобы длина перемещения оставалась положительной, даже, если движение происходит влево по оси, т. е. против направления оси Ox.
Сравним два случая движения тел. Первый – в положительном направлении оси Ox (рис 2а), второй – в направлении, противоположном оси (рис 2б).
Рис. 2. Перемещение вправо по оси – а) и влево по оси – б)
Чтобы найти длину вектора перемещения при движении в положительном направлении оси (рис. 2а), модуль раскрываем так:
[ S = left| x — x_{0} right| = x — x_{0} ]
Для движения в отрицательном направлении оси (рис. 2б), длина вектора перемещения выражается так:
[ S = left| x — x_{0} right| = — left( x — x_{0} right) = x_{0} — x ]
И в первом, и во втором случае, длина (модуль) вектора перемещения окажется положительной.
Скорость равномерного движения
В учебниках физики равномерному движению дают такое определение:
Движение равномерное, когда тело за одинаковые интервалы времени проходит равные расстояния.
Упростим формулировку:
Если каждую секунду тело проходит одинаковые расстояния – оно движется равномерно.
Слово «равномерное» состоит из двух частей.
Если разбить его на части, получим
«равно» — одинаковый, равный,
«мерное» — отмерять.
Или, другими словами: каждую секунду отмеряем одинаковые расстояния (рис. 2).
Рис. 3. Если тело проходит равные пути за одинаковые кусочки времени, движение будет равномерным
Для равномерного движения тела его
- перемещение,
- время движения и
- скорость,
связаны соотношением:
[ left|vec{S} right| = left|vec{v} right|cdot t ]
Эта формула называется уравнением движения. Или, развернуто: «уравнение равномерного прямолинейного движения».
Где ( left|vec{S} right| ) — длина (модуль) вектора перемещения и, (left|vec{v} right|) — длина (модуль) вектора скорости.
Уравнение движения можно записать проще:
[ large boxed { S = v cdot t }]
(S left( text{м} right)) – расстояние, пройденное телом (перемещение).
(t left( c right)) – промежуток времени, в течение которого тело двигалось.
(v left( frac{text{м}}{c} right)) – скорость, с которой двигалось тело.
Разделив обе части уравнения ( S = v cdot t ) на интервал времени ( t ), получим выражение для скорости тела:
[ large boxed { frac{S}{t} = v }]
График уравнения равномерного движения
Вспомним, что перемещение является разностью конечных и начальных координат тела
( S = left| x — x_{0} right| )
Воспользуемся тем, что при движении вдоль положительного направления оси модуль можно раскрыть так:
( left| x — x_{0} right| = x — x_{0} )
Тогда уравнение движения перепишем так:
[ large boxed { x — x_{0} = v cdot t }]
Прибавим к обеим частям уравнения величину ( x_{0} ). Получим такую запись
[ large x = v cdot t + x_{0}]
Это уравнение задает на плоскости tOx линию. Ее график на осях «x» и «t» — это прямая линия.
Вспомним, что для прямой линии в математике применяют такой вид записи:
( y = k cdot x + b)
Сравним два уравнения:
[ begin{cases} x = vcdot t + x_{0}\ y = kcdot x + b end{cases} ]
Видно, что число ( x_{0}) – начальная координата тела, выполняет роль коэффициента (b).
А скорость тела ( v) – играет роль углового коэффициента (k).
Сравним графики линий (рис. 4), описанных соотношениями ( y = k cdot x + b) и ( x = v cdot t + x_{0})
Рис.4. При равномерном движении тела координата изменяется по линейному закону
Видно, что линия на рисунке 4а, располагается и слева и справа от вертикальной оси.
Линия же, описывающая движение тела, представленная на рисунке 4б, располагается только лишь в правой полуплоскости. Это не с проста. На горизонтальной оси рисунка 4б отложено время, а в левой полуплоскости время будет отрицательным. При решении задач физики мы считаем, что в начальный момент задачи время равно нулю. Поэтому, область отрицательного времени в физике нас не интересует.
Рассмотрим теперь на графике равномерное движение двух тел, обладающих разными скоростями (рис. 5). Движение тела 1 на рисунке описывает синяя линия, а тела 2 – красная.
Рис.5. Равномерное движение двух тел, обладающих разными скоростями. Скорость тела 1 (синий цвет) больше скорости тела 2 (линия красного цвета).
Два тела стартуют из точки ( x_{0}) и двигаются равномерно воль оси Ox. За промежуток времени ( Delta t) тело 1, проходит больший путь, чем тело 2.
Примечание: Чем сильнее на графике x(t) прямая линия прижимается к вертикали, тем больше скорость, с которой движется тело!
Как отмечалось выше, тело может двигаться не только в положительном направлении вдоль оси, но и в отрицательном направлении.
На следующем рисунке представлены случаи движения тела в положительном (рис. 6а) и, в отрицательном (рис. 6б) направлениях оси Ox.
Когда скорость направлена по оси (рис. 6а) — координата «x» увеличивается,
а когда против оси (рис. 6б) — координата «x» уменьшается.
Перемещение тела в положительном направлении оси – а) и в отрицательном направлении по оси Ox – б)
На рисунке рядом с прямыми x(t) приведены уравнения движения. Когда скорость направлена против оси (рис. 6б), перед ней записывают знак «минус».
Угол (alpha) на рисунке связан со знаком скорости. Если скорость направлена по оси (рис. 6а), то угол будет острым. А если скорость направлена против оси (рис. 6б) – угол тупой.
Примечание: Скорость – это вектор. Когда вектор направлен против оси, его проекция на эту ось будет отрицательной. Читайте тут о проекциях векторов. Длина любого вектора – это положительная величина.
Как по графику перемещения определить скорость
Пользуясь графиком функций S(t), или x(t) равномерного движения можно определить скорость, с которой движется тело.
Примечания:
- График S(t) называют так: «зависимость перемещения S от времени t», или кратко — график перемещения от времени.
- А график x(t) — так: «зависимость координаты x от времени t», или кратко — график координат от времени.
Скорость находим за четыре шага (рис. 7):
- Выбираем две точки на линии, описывающей движение и определяем их координаты;
- Находим разность вертикальных координат;
- После находим разность координат по горизонтали;
- Делим «вертикаль» на «горизонталь»
Полученное число и будет скоростью тела.
Примечания:
- Когда просят найти скорость, обычно имеют ввиду, что нужно найти модуль вектора скорости.
- Скорость в системе СИ измеряют в метрах, деленных на секунду.
Обращаем внимание на то, в каких единицах на осях измерены расстояние S и время t. Если нужно, переводим расстояние в метры, а время — в секунды, чтобы получить скорость в правильных единицах измерения.
Рис.7. Две точки 1 и 2 выбраны для того, чтобы по графику x(t) найти скорость равномерного прямолинейного движения тела
Рассмотрим рисунок 7.
На рисунке первая точка имеет координаты ( left( t_{1} ; x_{1} right) ),
координаты второй точки: ( left( t_{2} ; x_{2} right) ).
Разницы между координатами находим, руководствуясь принципом («конечная» — «начальная») по формулам
( Delta t = t_{2} — t_{1} )
( Delta x = x_{2} — x_{1} )
Скорость вычислим из соотношения
[ v = frac{Delta x}{Delta t}]
Читайте далее о том, как переводить скорость из километров в час в метры в секунду и о равнопеременном движении