Вектором является направленный отрезок. Длина этого отрезка является длиной вектора.
Длина вектора b⃗vec{b} обозначается ∣b⃗∣.left | vec{b} right |. Модуль числа имеет аналогичное обозначение и длина вектора часто называется модулем вектора.
Длина нулевого вектора равна нулю.
Нахождение длины вектора по его координатам
Длина вектора, который задан своими координатами, – это квадратный корень из суммы квадратов его координат.
Для того чтобы найти длину вектора, заданного своими координатами, нужно извлечь квадратный корень из суммы квадратов его координат.
- Для вектора b⃗=(bx;by),vec{b}=(b_{x};b_{y}), заданного на плоскости, длина вычисляется по формуле ∣b⃗∣left |vec{b} right|=bx2+by2sqrt {b_{x}^{2}+b_{y}^{2}}.
- Для вектора b⃗=(bx;by;bz),vec{b}=(b_{x};b_{y};b_{z}), заданного в пространстве, длина вычисляется по формуле ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}.
Пример 1
Найти длину вектора b⃗=(6;−4).vec{b}=(6;-4).
Вектор задан на плоскости, поэтому воспользуемся первой формулой: ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}}.
Подставим координаты вектора b⃗vec{b} в формулу, получим: ∣b⃗∣=62+(−4)2=36+16=52=213left | vec{b} right |=sqrt {6^{2}+(-4)^{2}}=sqrt {36+16}=sqrt {52}=2sqrt {13}.
Ответ: 2132sqrt {13}.
Пример 2
Найти длину вектора d⃗=(1;3;5).vec{d}=(1;3;5).
Вектор задан в пространстве, поэтому воспользуемся второй формулой:
∣d⃗∣=dx2+dy2+dz2left | vec{d} right |=sqrt {d_{x}^{2}+d_{y}^{2}+d_{z}^{2}}.
Подставим координаты вектора d⃗vec{d} в формулу, получим:
∣d⃗∣=12+32+52=1+9+25=35left | vec{d} right |=sqrt {1^{2}+3^{2}+5^{2}}=sqrt {1+9+25}=sqrt {35}.
Нахождение длины вектора по координатам точек его начала и конца
Для нахождения длины вектора CD⃗vec{CD}, где C(cx;cy)C(c_{x};c_{y}) и D(dx;dy)D(d_{x};d_{y}) существует определенная последовательность действий:
- Найти координаты вектора CD⃗vec{CD} по формуле: ∣CD⃗∣=(dx−cx;dy−cy)left | vec{CD} right |=(d_{x}-c_{x};d_{y}-c_{y}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}}.
Аналогично находится длина вектора CD⃗,vec{CD}, заданного в пространстве, где C(cx;cy;cz)C(c_{x};c_{y};c_{z}) и D(dx;dy;dz)D(d_{x};d_{y};d_{z}):
- Найти координаты вектора CD⃗vec{CD} по формуле: CD⃗=(dx−cx;dy−cy;dz−cz).vec{CD}=(d_{x}-c_{x};d_{y}-c_{y};d_{z}-c_{z}).
- Найти длину вектора по его координатам по формуле: ∣CD⃗∣=(dx−cx)2+(dy−cy)2+(dz−cz)2left | vec{CD} right |=sqrt {(d_{x}-c_{x})^{2}+(d_{y}-c_{y})^{2}+(d_{z}-c_{z})^{2}}.
Пример 1
На плоскости заданы точки E(−1;3)иK(3;−4)E(-1;3) и K(3;-4). Найти длину вектора EK⃗.vec{EK}.
Найдем координаты вектора EK⃗.vec{EK}. Для этого из координат конца вычтем координаты начала, получим:
EK⃗=(3−(−1);−4−3)=(3+1;−4−3)=(4;−7).vec{EK}=(3-(-1);-4-3)=(3+1;-4-3)=(4;-7).
Воспользуемся формулой ∣b⃗∣=bx2+by2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}} для нахождения длины вектора, получим:
∣EK⃗∣=42+(−7)2left | vec{EK} right |=sqrt {4^{2}+(-7)^{2}}=16+49sqrt {16+49}=65sqrt {65}.
Пример 2
В пространстве заданы точки C(1;2;3)C(1;2;3) и D(3;4;5).D(3;4;5). Найти длину вектора CD⃗.vec{CD}.
Найдем координаты вектора CD⃗.vec{CD}. Для этого из координат конца вычтем координаты начала, получим: CD⃗=(3−1;4−2;5−3)=(2;2;2).vec{CD}=(3-1;4-2;5-3)=(2;2;2).
Воспользуемся формулой ∣b⃗∣=bx2+by2+bz2left | vec{b} right |=sqrt {b_{x}^{2}+b_{y}^{2}+b_{z}^{2}} для нахождения длины вектора, получим: ∣b⃗∣=22+22+22=4+4+4=12=23left | vec{b} right |=sqrt {2^{2}+2^{2}+2^{2}}=sqrt {4+4+4}=sqrt {12}=2sqrt 3.
Нахождение длины вектора по теореме косинусов
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Для треугольника со сторонами a,b,ca, b, c и углами α,βalpha, beta и γ,gamma, противолежащими этим сторонам соответственно, справедливы равенства:
b=a2+c2−2a⋅c⋅cos(β),b=a^{2}+c^{2}-2acdot ccdot cos (beta), a=b2+c2−2b⋅c⋅cos(α),a=b^{2}+c^{2}-2bcdot ccdot cos (alpha), c=a2+b2−2a⋅b⋅cos(γ).c=a^{2}+b^{2}-2acdot bcdot cos (gamma).
Аналогично поступают и с векторами. Рассмотрим пример.
Пример 1
Длины векторов KL⃗vec{KL} и KM⃗vec{KM} равны соответственно 2 и 4, а угол между ними равен π4.frac{pi }{4}. Вычислите длину вектора LM⃗.vec{LM}.
Длина вектора LM⃗vec{LM} равна длине стороны LMLM в треугольнике LMKLMK. Также нам известны стороны KLKL и KMKM треугольника LMKLMK. Они равны длинам соответствующих векторов. Нам известен угол между векторами. Найдем сторону LMLM треугольника △KLM.triangle KLM.
LM2=KL2+KM2−2KL⋅KM⋅cos∠LKM.LM^2=KL^2+KM^2-2KLcdot KMcdot cos angle LKM.
LM2=22+42−2⋅2⋅4⋅cosπ4=4+16−82=20−82.LM^2=2^2+4^2-2cdot 2cdot4cdot cos frac{pi }{4}=4+16-8sqrt{2}=20-8sqrt{2}.
LM=20−82.LM=sqrt{20-8sqrt{2}}.
∣LM⃗∣=20−82.|vec{LM}|=sqrt{20-8sqrt{2}}.
Тест по теме «Как вычислить длину вектора»
Длина вектора
Как найти?
Длина вектора $ overline{a}$ обозначается как $ |overline{a}| $. Как найти длину вектора по его координатам? Для этого существует две формулы в зависимости от расположения вектора: на плоскости $ overline{a}=(a_x;a_y) $ или в пространстве $ overline{a} = (a_x; a_y; a_z) $.
Формула длины вектора на плоскости:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2} $$
Формула длины вектора в пространстве:
$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2 + a_z ^2 } $$
Если даны координаты точек начала и конца вектора $ A(a_x; a_y) $ и $ B(b_x; b_y) $, то найти длину можно по формулам:
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y) ^2} $$
$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y)^2+ (a_z-b_z)^2} $$
Примеры решений
| Пример 1 |
| Найти длину вектора по его координатам $ overline{a} = (4;-3) $ |
| Решение |
|
Разберем вектор. Первая координата $ a_x = 4 $, а вторая координата $ a_y=-3 $. Так как даны две координаты, то делаем вывод, что задача плоская. Необходимо применить первую формулу. Подставляем в неё значения из условия задачи: $$|overline{a}| = sqrt{4^2+(-3)^2} = sqrt{16+9} = sqrt{25} = 5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| Длина вектора $|overline{a}| = 5 $ |
| Пример 2 |
| Найти длину вектора по координатам $ overline{a}=(4;2;4) $ |
| Решение |
|
Сразу замечаем, что дана пространственная задача. А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё: $|overline{a}|=sqrt{4^2+2^2+4^2}=sqrt{36}=6 $ |
| Ответ |
| Длина вектора $|overline{a}|=6 $ |
| Пример 3 |
| Найти длину вектора, если известны координаты его начала и конца. $ A=(2;1), B=(-1;3) $ |
| Решение |
|
Задача дана плоская судя по наличию только двух координат у векторов. Но даны на этот раз начало и конец вектора. Поэтому сначала находим координаты вектора $ overline{AB} $, а только потом его длину по формуле координат: $ overline{AB}=(b_x-a_x;b_y-a_y)=(-1-2;3-1)=(-3;2) $ Теперь когда координаты вектора $ overline{AB} $ стали известны можно использовать привычную формулу: $|overline{AB}|=sqrt{(-3)^2+2^2}=sqrt{9+4}=sqrt{13} $ |
| Ответ |
| $|overline{AB}|=sqrt{13} $ |
В статье мы ответили на вопрос:»Как найти длину вектора?» с помощью формул. А также рассмотрели практические примеры решения задач на плоскости и в пространстве. Следует заметить, что существуют аналогичные формулы для пространств больше, чем трёхмерные.
При решении различных задач в геометрии возникает необходимость определить длину заданного вектора. Для того чтобы ее найти, нужно знать координаты начальной и конечной точки направленного отрезка. Далее все расчеты производятся по формуле, которую достаточно легко вывести, если правильно применить теорему Пифагора.
Понятие длины вектора
Прежде чем перейти к определению длины вектора, необходимо разъяснить само понятие «вектор». В геометрии оно используется для обозначения такого объекта, который характеризуется направлением и величиной. Его можно представить в виде отрезка. Далее необходимо пояснить то, как он выглядит на плоскости.
Определения 1 — 5
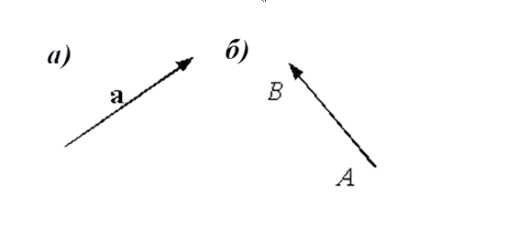
Отрезком в геометрии называют какую-то часть прямой, ограниченную двумя точками. У него может быть всего два направления, для обозначения которых используются такие понятия как начало и конец отрезка, которые соответствуют его границам. Направление принято указывать от начала отрезка к его концу.
Называть отрезок вектором можно в том случае, если известно, какая из двух его границ является началом, а какая – концом.
В геометрии он может обозначаться двумя буквами, соответствующими его началу и концу.
Если обозначается как [vec{A B}], то A – это начало отрезка, а B – соответственно его конец.
Также допустимо обозначение в виде одной строчной буквы, например [vec{a}]. На рисунке показано как это выглядит на плоскости.
После того, как стало понятно, что такое вектор и как он обозначается, можно переходить к определению его длины.
Понятие длины вектора [vec{a}] используется для обозначения размера направленного отрезка. Она обозначается, как [|vec{a}|].
При решении задач в геометрии необходимо знать, в каких случаях применимо понятие равенство двух векторов.
Для того чтобы можно было назвать два вектора равными, должны соблюдаться два определенных условия:
- они являются сонаправленными;
- длина одного равна длине другого.
Определять векторы можно только в том случае, если введена система координат и ней у направленных отрезков имеются точные координаты.
Любой вектор независимо от его обозначения и длины можно разложить следующим образом:
[vec{c}=m vec{i}+n vec{j}], где m и n — это какие-то действительные числа, а [vec{i}] и [vec{j}] – это два единичных вектора, расположенных непосредственно на осях [O x] и [O y].
Координатами рассматриваемого вектора [vec{c}=vec{mi}+vec{nj}] в введенной нами прямоугольной системе координат будут являться коэффициенты его разложения. В математическом виде это записывается следующим образом:
[bar{c}=m, n]
Формула длины вектора
Для того чтобы определить длину произвольного вектора, необходимо вывести формулу на основании точных данных координат этого отрезка в квадратной системе координат.
Чтобы понять, как это сделать, рассмотрим соответствующую задачу.
Пример
Координаты заданного вектора [vec{a}-x, y]. Требуется определить его длину по указанным данным.
Решение:
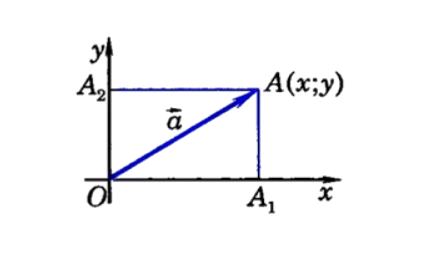
Для того чтобы приступить к решения примера требуется ввести на плоскости систему координат [x O y]. Далее нужно будет отложить в введенной системе координат [vec{OA}=vec{a}]. После этого можно приступить к построению проекций [O A_{1}] и [O A_{2}], направленного отрезка, которой расположен на оси [O x] и [O y] так, как показано на рисунке ниже.
[vec{OA}] будет для точки A радиус вектором. Это означает, что она будет иметь следующие координаты — x, y. Исходя из этого можно сделать вывод, что [left[O A_{1}right]=x,left[O A_{2}right]=y].
Для того чтобы определить длину, применяем теорему Пифагора. В результате получаем:
[begin{aligned}
&left| vec{a}right|^{2}=left[mathrm{OA}_{1}right]^{2}+left[mathrm{OA}_{2}right]^{2} \
&left.|vec{a}right|^{2}=x^{2}+y^{2} \
&left.|vec{ a}right|^{2}=sqrt{x^{2}+y^{2}}
end{aligned}]
Ответ: Искомая длина заданного вектора определяется по формуле [left.|vec{a}right|^{2}=sqrt{x^{2}+y^{2}}]
На основании рассмотренного примера можно сделать вывод, что для определения длины какого-либо вектора, у которого известны координаты, следует найти корень из суммы квадратов заданных координат.
Нет времени решать самому?
Наши эксперты помогут!
Примеры задач
Задачи 1 — 2
Требуется определить расстояние между двумя точками X и Y, координаты которых (−1,7) и (8,4), соответственно.
Решение. Известно, что любые две точки на плоскости можно связать с понятием направленного отрезка. В данном случае мы будем рассматривать вектор [vec{X Y}]. Как было сказано ранее, координаты определяются путем вычитания координат конца отрезка [(Y)] из соответствующих координат его начальной точки [(X)].
Применяя это правило, получаем: [vec{X Y}=(8+1,4-7)=(9-3)]
Затем, чтобы найти искомую длину, применим формулу, выведенную нами ранее.
Получаем: [d=sqrt{9^{2}+(-3)^{2}}=sqrt{81+9}=sqrt{90}=3 sqrt{10}]
Ответ: Длина вектора равна [3 sqrt{10}]
Важно! Эта задача позволяет вывести формулу для определения расстояния между начальной и конечной точками. Пусть они имеют следующие координаты [left(x^{prime}, y^{prime}right)] и [left(x^{prime prime}, y^{prime prime}right)]. Тогда определить длину между этими точками можно с помощью формулы:
[d=left(mathrm{x}^{prime}-mathrm{x}^{prime prime}right) 2+left(y^{prime}-y^{prime prime}right)]
Пусть нам дан один треугольник и известны координаты его вершин (6,-10),(13,-3),(5,0). Требуется найти периметр фигуры.
Решение. Сначала найдем длины сторон треугольника, используя выведенную формулу.
Длина первой стороны равна: [sqrt{(6-13)^{2}+(-10+3)^{2}}=sqrt{(-7)^{2}+(-7)^{2}}=sqrt{98}=7 sqrt{2} .]
Вторая сторона треугольника будет равна: [sqrt{(6-5)^{2}+(-10-0)^{2}}=sqrt{1^{2}+(-10)^{2}}=sqrt{101}].
Третья сторона треугольника равняется: [sqrt{(13-5)^{2}+(-3-0)^{2}}=sqrt{8^{2}+(-3)^{2}}=sqrt{73}].
Сложив все три стороны, получим длину периметра рассматриваемого треугольника.
Ответ: [7 sqrt{2}+sqrt{101}+sqrt{73}].
Заключение. В процессе решения задач мы вывели формулу длины вектора, и научились применять ее для определения периметра геометрических фигур.
Как найти длину вектора
ФОРМУЛА
Чтобы найти длину вектора, определяемого его координатами, вам нужно извлечь квадратный корень из суммы квадратов его координат. Если вектор определен на плоскости и имеет координаты (
overline{a}=left(a_{x} ; a_{y}right)
), его длина рассчитывается по формуле:
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}
)
Если вектор задан в пространстве координатами (
overline{a}=left(a_{x} ; a_{y} ; a_{z}right)
) , то его длина вычисляется по формуле
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}
)
ПРИМЕРЫ РАСЧЕТА ВЕКТОРНОЙ ДЛИНЫ
ПРИМЕР
overline{a}=(-3 ; 4)
)
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}
)
Подставляя в него координаты заданного вектора, получаем:
(
|overline{a}|=sqrt{(-3)^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5
)
|overline{a}|=5
)
ПРИМЕР
A(3 ;-2 ;-1)quad{и}quad B(1 ; 2 ;-5)
). Найти длину вектора (
overline{A B}
)
overline{A B}
). Для этого из координат конца мы вычисляем соответствующие координаты начала, получаем:
(
overline{A B}=(1-3 ; 2-(-2) ;-5-(-1))=(-2 ; 4 ;-4)
)
Находя длину вектора (
overline{A B}
) мы используем формулу:
(
|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}
)
Подставляя в эту формулу координаты вектора, получим
(
|overline{A B}|=sqrt{(-2)^{2}+4^{2}+(-4)^{2}}=sqrt{4+16+16}=sqrt{36}=6
)
|overline{A B}|=6
)
Содержание:
- Формула
- Примеры вычисления длины вектора
Формула
Чтобы найти длину вектора, заданного своими координатами, нужно извлечь корень квадратный из суммы квадратов его координат.
Если вектор задан на плоскости и имеет координаты $bar{a}=left(a_{x} ; a_{y}right)$, его длина вычисляется по формуле:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Если вектор задан в пространстве координатами $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$, то его длина вычисляется по формуле
$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$
Примеры вычисления длины вектора
Пример
Задание. Найти длину вектора $bar{a}=(-3 ; 4)$
Решение. Для нахождения длины вектора, заданного на плоскости, воспользуемся формулой
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Подставляя в неё координаты заданного вектора, получим:
$$|bar{a}|=sqrt{(-3)^{2}+4^{2}}=sqrt{9+16}=sqrt{25}=5$$
Ответ. $|bar{a}|=5$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданы точки
$A(3 ;-2 ;-1)$ и $ B(1 ; 2 ;-5)$. Найти длину вектора
$overline{A B}$
Решение. Найдем сначала координаты вектора $overline{A B}$. Для этого из координат конца вычислим соответствующие координаты начала, получим:
$$overline{A B}=(1-3 ; 2-(-2) ;-5-(-1))=(-2 ; 4 ;-4)$$
нахождения длины вектора $overline{A B}$ воспользуемся формулой:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$$
Подставляя в эту формулу координаты вектора, получим
$$|overline{A B}|=sqrt{(-2)^{2}+4^{2}+(-4)^{2}}=sqrt{4+16+16}=sqrt{36}=6$$
Ответ. $|overline{A B}|=6$
Читать дальше: как найти модуль вектора.