Как найти длину вектора в стереометрии

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

Разность векторов:

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1.  В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2.  В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и :

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

.

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

;

.

Выразим C и B через A и подставим в третье уравнение:

.

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Упростим систему:

.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор  или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

  

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

План урока:

Прямоугольная система координат

Координаты вектора

Координаты середины отрезка

Вычисление длины векторов и расстояния между точками

Коллинеарность векторов

Определение компланарности векторов

Скалярное произведение векторов

Прямоугольная система координат

В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.

В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.

Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.

Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:

Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.

На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.

Координаты вектора

Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а{3; – 2; – 4}.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.

Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.

Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а{3; 7; 5} и b{2; 4; 6}.

Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это х_а, у_а и z_а. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты {0; – 2; 3}.

Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

ч. т. д.

Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).

Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m{3; 2; 5}, конец совпал в точку H. Найдите коорд-ты точки H.

Решение. Коорд-ты вектора m и его концов связаны формулами:

Координаты середины отрезка

Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:

Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:

Аналогично можно получить аналогичные формулы для коорд-т у и z:

Рассмотрим несколько задач на координаты точек.

Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).

Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:

Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.

Решение. Сначала запишем формулу для коорд-ты х:

Вычисление длины векторов и расстояния между точками

Рассмотрим радиус-вектор ОМ с коорд-тами {x; у; z}. Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами {x; y; z} будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m{– 2; 9; 6}.

Решение. Просто используем формулу:

Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:

Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).

Решение. Просто подставляем коорд-ты точек в формулу:

Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).

Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Определение компланарности векторов

Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.

Задание. Определите, компланарны ли вектора

Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.

Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.

Скалярное произведение векторов

В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.

Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.

Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:

Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов а{x_а; у_а} и b{х_b; y_b} можно было рассчитать так:

Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.

Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).

Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:

Задание. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁ ребра имеют длину:

AB = 1

BC = 2

BB₁ = 2

Рассчитайте угол между векторами DB₁ и BC₁.

Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB₁ и BC₁:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.

Ответ: 90°

Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.

Нахождение длины вектора, примеры и решения

Длина вектора — основные формулы

Длину вектора a → будем обозначать a → . Данное обозначение аналогично модулю числа, поэтому длину вектора также называют модулем вектора.

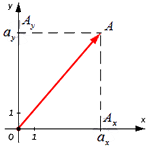
Для нахождения длины вектора на плоскости по его координатам, требуется рассмотреть прямоугольную декартову систему координат O x y . Пусть в ней задан некоторый вектор a → с координатами a x ; a y . Введем формулу для нахождения длины (модуля) вектора a → через координаты a x и a y .

От начала координат отложим вектор O A → = a → . Определим соответственные проекции точки A на координатные оси как A x и A y . Теперь рассмотрим прямоугольник O A x A A y с диагональю O A .

Из теоремы Пифагора следует равенство O A 2 = O A x 2 + O A y 2 , откуда O A = O A x 2 + O A y 2 . Из уже известного определения координат вектора в прямоугольной декартовой системе координат получаем, что O A x 2 = a x 2 и O A y 2 = a y 2 , а по построению длина O A равна длине вектора O A → , значит, O A → = O A x 2 + O A y 2 .

Отсюда получается, что формула для нахождения длины вектора a → = a x ; a y имеет соответствующий вид: a → = a x 2 + a y 2 .

Если вектор a → дан в виде разложения по координатным векторам a → = a x · i → + a y · j → , то вычислить его длину можно по той же формуле a → = a x 2 + a y 2 , в данном случае коэффициенты a x и a y выступают в роли координат вектора a → в заданной системе координат.

Вычислить длину вектора a → = 7 ; e , заданного в прямоугольной системе координат.

Чтобы найти длину вектора, будем использовать формулу нахождения длины вектора по координатам a → = a x 2 + a y 2 : a → = 7 2 + e 2 = 49 + e

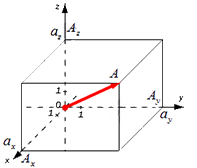
Формула для нахождения длины вектора a → = a x ; a y ; a z по его координатам в декартовой системе координат Oxyz в пространстве, выводится аналогично формуле для случая на плоскости (см. рисунок ниже)

В данном случае O A 2 = O A x 2 + O A y 2 + O A z 2 (так как ОА – диагональ прямоугольного параллелепипеда), отсюда O A = O A x 2 + O A y 2 + O A z 2 . Из определения координат вектора можем записать следующие равенства O A x = a x ; O A y = a y ; O A z = a z ; , а длина ОА равна длине вектора, которую мы ищем, следовательно, O A → = O A x 2 + O A y 2 + O A z 2 .

Отсюда следует, что длина вектора a → = a x ; a y ; a z равна a → = a x 2 + a y 2 + a z 2 .

Вычислить длину вектора a → = 4 · i → — 3 · j → + 5 · k → , где i → , j → , k → — орты прямоугольной системы координат.

Дано разложение вектора a → = 4 · i → — 3 · j → + 5 · k → , его координаты равны a → = 4 , — 3 , 5 . Используя выше выведенную формулу получим a → = a x 2 + a y 2 + a z 2 = 4 2 + ( — 3 ) 2 + 5 2 = 5 2 .

Длина вектора через координаты точек его начала и конца

Выше были выведены формулы, позволяющие находить длины вектора по его координатам. Мы рассмотрели случаи на плоскости и в трехмерном пространстве. Воспользуемся ими для нахождения координат вектора по координатам точек его начала и конца.

Итак, даны точки с заданными координатами A ( a x ; a y ) и B ( b x ; b y ) , отсюда вектор A B → имеет координаты ( b x — a x ; b y — a y ) значит, его длина может быть определена по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2

А если даны точки с заданными координатами A ( a x ; a y ; a z ) и B ( b x ; b y ; b z ) в трехмерном пространстве, то длину вектора A B → можно вычислить по формуле

A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2

Найти длину вектора A B → , если в прямоугольной системе координат A 1 , 3 , B — 3 , 1 .

Используя формулу нахождения длины вектора по координатам точек начала и конца на плоскости, получим A B → = ( b x — a x ) 2 + ( b y — a y ) 2 : A B → = ( — 3 — 1 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 .

Второй вариант решения подразумевает под собой применение данных формул по очереди: A B → = ( — 3 — 1 ; 1 — 3 ) = ( — 4 ; 1 — 3 ) ; A B → = ( — 4 ) 2 + ( 1 — 3 ) 2 = 20 — 2 3 . —

Ответ: A B → = 20 — 2 3 .

Определить, при каких значениях длина вектора A B → равна 30 , если A ( 0 , 1 , 2 ) ; B ( 5 , 2 , λ 2 ) .

Для начала распишем длину вектора A B → по формуле: A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 = ( 5 — 0 ) 2 + ( 2 — 1 ) 2 + ( λ 2 — 2 ) 2 = 26 + ( λ 2 — 2 ) 2

Затем полученное выражение приравняем к 30 , отсюда найдем искомые λ :

26 + ( λ 2 — 2 ) 2 = 30 26 + ( λ 2 — 2 ) 2 = 30 ( λ 2 — 2 ) 2 = 4 λ 2 — 2 = 2 и л и λ 2 — 2 = — 2 λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Ответ: λ 1 = — 2 , λ 2 = 2 , λ 3 = 0 .

Нахождение длины вектора по теореме косинусов

Увы, но в задачах не всегда бывают известны координаты вектора, поэтому рассмотрим другие способы нахождения длины вектора.

Пусть заданы длины двух векторов A B → , A C → и угол между ними (или косинус угла), а требуется найти длину вектора B C → или C B → . В таком случае, следует воспользоваться теоремой косинусов в треугольнике △ A B C , вычислить длину стороны B C , которая и равна искомой длине вектора.

Рассмотрим такой случай на следующем примере.

Длины векторов A B → и A C → равны 3 и 7 соответственно, а угол между ними равен π 3 . Вычислить длину вектора B C → .

Длина вектора B C → в данном случае равна длине стороны B C треугольника △ A B C . Длины сторон A B и A C треугольника известны из условия (они равны длинам соответствующих векторов), также известен угол между ними, поэтому мы можем воспользоваться теоремой косинусов: B C 2 = A B 2 + A C 2 — 2 · A B · A C · cos ∠ ( A B , → A C → ) = 3 2 + 7 2 — 2 · 3 · 7 · cos π 3 = 37 ⇒ B C = 37 Таким образом, B C → = 37 .

Итак, для нахождения длины вектора по координатам существуют следующие формулы a → = a x 2 + a y 2 или a → = a x 2 + a y 2 + a z 2 , по координатам точек начала и конца вектора A B → = ( b x — a x ) 2 + ( b y — a y ) 2 или A B → = ( b x — a x ) 2 + ( b y — a y ) 2 + ( b z — a z ) 2 , в некоторых случаях следует использовать теорему косинусов.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Прямоугольная система координат

В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.

В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.

Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.

Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:

Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.

На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.

Координаты вектора

Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.

Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:

где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а<3; – 2; – 4>.

Задание. Разложите на орты вектор

Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.

Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.

Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.

Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:

Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:

Задание. Найдите сначала сумму, а потом разность векторов а <3; 7; 5>и b<2; 4; 6>.

Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это х_а, у_а и z_а. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:

Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:

Задание. Вычислите коорд-ты вектора р, зная, что:

Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:

Получается, что вектор p имеет координаты <0; – 2; 3>.

Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:

Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:

Координаты радиус-векторов будут совпадать с координатами их концов:

Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).

Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:

Задание. От точки K(10; 6; 13) отложен вектор m<3; 2; 5>, конец совпал в точку H. Найдите коорд-ты точки H.

Решение. Коорд-ты вектора m и его концов связаны формулами:

Координаты середины отрезка

Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:

Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:

Аналогично можно получить аналогичные формулы для коорд-т у и z:

Рассмотрим несколько задач на координаты точек.

Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).

Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:

Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.

Решение. Сначала запишем формулу для коорд-ты х:

Вычисление длины векторов и расстояния между точками

Рассмотрим радиус-вектор ОМ с коорд-тами . Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:

Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:

Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.

Задание. Найдите длину вектора m<– 2; 9; 6>.

Решение. Просто используем формулу:

Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:

Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).

Решение. Просто подставляем коорд-ты точек в формулу:

Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).

Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:

Коллинеарность векторов

Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что

Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:

Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть

В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами <0; 0; 0>. Он условно признается коллинеарным любому вектору.

Задание. Выясните, какие из этих пар векторов коллинеарны:

Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:

Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.

Повторяем эти действия в задании б):

На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.

В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.

В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:

Коэффициент k получился одинаковым, поэтому вектора коллинеарны.

В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.

Ответ: а) да; б) нет; в) нет; г) да; д) да.

Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).

Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.

Сначала вычислим коорд-ты векторов АВ и ВС:

Теперь проверяем, коллинеарны ли эти вектора:

Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.

Определение компланарности векторов

Пусть у нас есть три вектора с известными коорд-тами:

Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:

где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:

Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.

Задание. Определите, компланарны ли вектора

Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:

Значит, рассмотренная тройка векторов компланарна.

Задание. Располагаются ли в одной плос-ти вектора:

Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:

Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.

Скалярное произведение векторов

В 9 классе мы уже изучали скалярное произведение векторов.

Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.

Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.

Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:

Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:

Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов аа; у_а> и b<х_b; y_b> можно было рассчитать так:

Задание. Вычислите скалярное произведение векторов:

На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.

Задание. Вычислите угол между векторами:

Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:

Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).

Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:

Далее рассчитываем скалярное произведение векторов:

Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:

Задание. В прямоугольном параллелепипеде АВСDA₁B₁C₁D₁ ребра имеют длину:

Рассчитайте угол между векторами DB₁ и BC₁.

Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:

При этом построении граничные точки векторов будут иметь следующие коорд-ты:

Находим коорд-ты векторов, а также их длины:

Рассчитываем скалярное произведение DB₁ и BC₁:

Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.

Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix 

Заказать задачи по любым предметам можно здесь от 10 минут

Длина вектора

Как найти?

Длина вектора $ overline{a}$ обозначается как $ |overline{a}| $. Как найти длину вектора по его координатам? Для этого существует две формулы в зависимости от расположения вектора: на плоскости $ overline{a}=(a_x;a_y) $ или в пространстве $ overline{a} = (a_x; a_y; a_z) $.

Формула длины вектора на плоскости:

$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2} $$

Формула длины вектора в пространстве:

$$ |overline{a}| = sqrt{a_x ^2 + a_y ^2 + a_z ^2 } $$

Если даны координаты точек начала и конца вектора $ A(a_x; a_y) $ и $ B(b_x; b_y) $, то найти длину можно по формулам:

$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y) ^2} $$

$$ |overline{AB}| = sqrt{(a_x-b_x)^2 + (a_y-b_y)^2+ (a_z-b_z)^2} $$

Примеры решений

Пример 1

Найти длину вектора по его координатам $ overline{a} = (4;-3) $

Решение

Разберем вектор. Первая координата $ a_x = 4 $, а вторая координата $ a_y=-3 $. Так как даны две координаты, то делаем вывод, что задача плоская. Необходимо применить первую формулу. Подставляем в неё значения из условия задачи: $$|overline{a}| = sqrt{4^2+(-3)^2} = sqrt{16+9} = sqrt{25} = 5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

Длина вектора $|overline{a}| = 5 $

Пример 2

Найти длину вектора по координатам $ overline{a}=(4;2;4) $

Решение

Сразу замечаем, что дана пространственная задача. А именно $ a_x=4, a_y=2, a_z=4 $. Для нахождения длины вектора используем вторую формулу. Подставляем неизвестные в неё: $|overline{a}|=sqrt{4^2+2^2+4^2}=sqrt{36}=6 $

Ответ

Длина вектора $|overline{a}|=6 $

Пример 3

Найти длину вектора, если известны координаты его начала и конца. $ A=(2;1), B=(-1;3) $

Решение

Задача дана плоская судя по наличию только двух координат у векторов. Но даны на этот раз начало и конец вектора. Поэтому сначала находим координаты вектора $ overline{AB} $, а только потом его длину по формуле координат: $ overline{AB}=(b_x-a_x;b_y-a_y)=(-1-2;3-1)=(-3;2) $ Теперь когда координаты вектора $ overline{AB} $ стали известны можно использовать привычную формулу: $|overline{AB}|=sqrt{(-3)^2+2^2}=sqrt{9+4}=sqrt{13} $

Ответ

$|overline{AB}|=sqrt{13} $

В статье мы ответили на вопрос:»Как найти длину вектора?» с помощью формул. А также рассмотрели практические примеры решения задач на плоскости и в пространстве. Следует заметить, что существуют аналогичные формулы для пространств больше, чем трёхмерные.